2. 中国石油长庆油田分公司 第五采气厂, 西安 710016;
3. 中国地质大学(北京)数理学院, 北京 100083
2. No.5 Gas Production Plant, PetroChinaChangqing Oilfield Company, Xi'an 710016, China;
3. School of Science, China University of Geosciences, Beijing 100083, China
测井岩性识别是储层评价的重要工作,测井资料中包含着丰富的岩性信息,随着数学理论的发展和计算能力的提高,利用测井资料结合计算机技术判别岩性已成为测井技术人员高度关注的内容[1]。通过对测井数据的定性、定量解释,地质学家建立了测井参数和所需储层信息的匹配关系,并对目标储层进行预测。以复杂碳酸盐岩岩性识别为例,多元统计方法[2]、主成分分析技术[3-4]、模糊数学[2]、支持向量机[5]和人工神经网络[4, 6]等方法在生产实践中被广泛应用,但是这些方法在提高目标体预测准确率的同时,也出现了一些问题,如BP神经网络方法难以解释输出节点之间的关系,并且难以将地质知识结合到网络中[7];同时,BP模型往往简化了现实条件,将地质学家面对的工作简单处理为一个函数寻优过程,这使得地质工作者无法了解和控制中间过程,当出现算法结果和地质经验相冲突时,很难通过局部调整来寻求两者的统一。
据文献[8]报道,自组织映射(Self-Organizing Map,SOM)是Kohonen在1982年发明的一种数据降维聚类技术,该方法通过“拓扑保持映射”的方法将高维度相似输入数据映射到彼此接近的映射区域,进而挖掘隐藏在数据中的组织结构[9]。这些组织结构揭示了关于自然群体的分类结构的重要信息,而其他方法很难获得这些信息。该方法已经用于许多领域,例如金融、工业控制、语音分析和天文学[10-11]。Roy等[12]描述了该神经网络自20世纪90年代后期以来在地质行业中如何使用以解决各种地球科学解释问题。在以往的地学应用中,地质工作者往往仅关注SOM的降维作用和聚类能力,对其保拓扑结构的作用分析不足。采用SOM挖掘测井参数的关系信息和拓扑结构,同时将模糊识别的原理结合起来,利用专家信息,对分类规则进行有监督校正,以期既能够体现数据的本来特征,也在模型中融入监督信息,使判断的准确性较同类方法得到有效提升。
1 地质背景苏里格气田苏东41-33区块位于苏里格东区西部,西与苏5区块接壤、西北部接苏25区块、西南接苏6区块,区域构造属于陕北斜坡北部,主要勘探目的层位为石盒子组、山西组砂岩和马家沟组碳酸盐岩。该地区碳酸盐岩储层受岩溶古地貌、沉积、成岩等因素影响,储层普遍具有低孔、低渗、非均质性强等特征,其特性致使该地区的碳酸盐岩储量探明率整体较低,具有良好的勘探开发前景[13-14]。
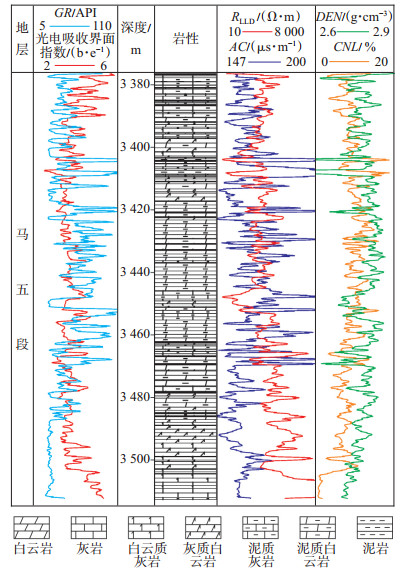
应用常规测井资料对储层进行评价,必须在储层四性关系研究的基础之上进行。储层内岩性、含气性和物性之间既存在联系又相互制约,其中岩性起主导作用,因此岩性的精准识别是储层评价中至关重要的一步[15-16]。通过袁照威等[1]的研究和测录井资料分析(图 1),该地区岩石类型主要发育灰岩、白云质灰岩、泥质灰岩、白云岩、灰质白云岩、泥质白云岩和泥岩等7种类型,同时选择对岩性较为敏感的声波时差、自然伽马、补偿中子、密度、光电吸收截面指数和电阻率等6种测井资料[1, 3],应用于岩性精准分类。
|
下载eps/tif图 图 1 不同岩性类型测录井曲线响应特征 Fig. 1 Logging curve response characteristics of different lithologies |
如图 1所示,不同岩性具有不同的测井参数特征,自然伽马曲线能够将泥岩和其他几种类型明显区分开,泥岩自然伽马多大于96 API,所以研究过程中重点分析其他6种类型的测井参数。泥质灰岩和泥质白云岩2种类型由于泥质含量较高,自然伽马值相对较高;灰岩的光电吸收界面指数值高于其他几种类型;对于电阻率曲线而言,灰岩和白云质灰岩呈现出高值特征,当含泥量增加时,泥质灰岩和泥质白云岩的电阻率降低;对于密度曲线而言,白云岩相对于灰云岩表现出较高的参数特征。
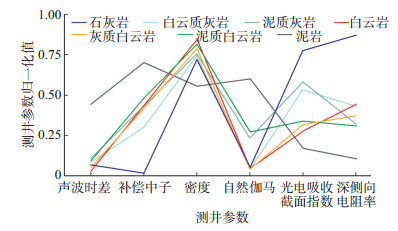
虽然不同岩性在测井参数上存在一定的差异,但是不同岩性的测井参数构成的样本特征空间存在着较多的重叠(图 2),用常规手段难以判断岩性归属的问题。在实际工区中,地质工作者使用的测井参数种类较多,难以把握数据在高维空间中的分布特征,对测井数据的相互关系也缺乏直观的解读。因此,马家沟组碳酸盐岩储层岩性识别较为困难。
|
下载eps/tif图 图 2 不同岩性测井参数平行坐标图(均值) Fig. 2 Parallel coordinates of logging parameters of different lithologies |
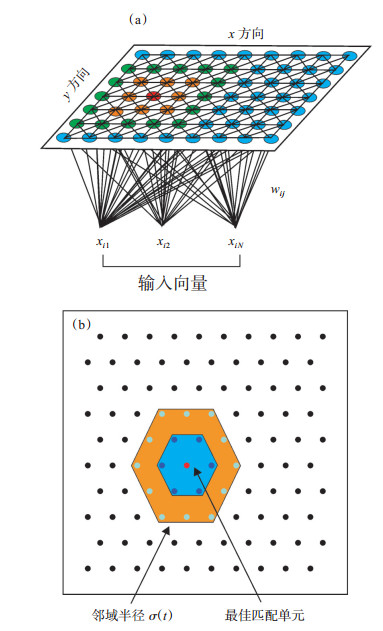
SOM是具有权重矩阵的两层全连接结构的神经元网络,在分析高维变量问题时,实验者往往不能一次性的获得多种数据簇之间的关系,SOM可以通过生成与原始数据具有相似性的二维拓扑结构来达到降维的目的[8][图 3(a)]。SOM向神经元分配初始值,然后对于每个多属性样本通过欧式距离找到最接近该样本的神经元,并且修正神经元的权重,网格中附近的其他神经元也同步修正[图 3(b)]。对训练集中的每个样本重复该过程,从而完成一次SOM学习。衡量SOM算法是否收敛的一个重要依据是神经元修正的程度,当达到收敛条件或者迭代次数后,整个SOM的学习将结束[8]。
|
下载eps/tif图 图 3 自组织映射结构图(a)及权重向量调整示意图(b) Fig. 3 SOM structural diagram chart (a) and weight vector adjustment diagram (b) |
自组织映射算法执行以下3个过程[14]:
(1)竞争:对每个输入矢量,网络中的神经元计算各自的判别函数的值,具有判别函数最大值的神经元成为竞争的获胜者。
(2)合作:获胜神经元决定输入矢量在拓扑邻域的空间位置,并激活相邻近的神经元。
(3)调节:随着算法的迭代,对输入矢量对应的最佳匹配单元进行局部调整,使它们对相似输入矢量的响应增强。
SOM采用竞争Hebb学习规则来建立神经元之间的连接,Ritter等[17]已经证明用这种方法建立的连接,能够形成神经元集合的Delaunay三角剖分的子图。同时,这种子图在神经元足够稠密的条件下,能够完美保持原始数据的拓扑邻域关系。具体实现步骤如下[10]:
(1)输入空间X为N维向量空间xi ∈ X,xi =[xi1,xi2, …, xiN]。其中xi表示第i个测井样本,N为需要进行分析的测井参数个数。
(2)确定输出网格大小为m行n列,随机生成l = m × n个网格节点,每个网格节点代表一个权重向量,记为wj,其中j = 1,2,…,l。
(3)在第t次迭代过程中,在输入空间随机选取向量xi ∈ X作为输入向量。
(4)计算xi到所有权重向量的欧式距离,选取距离最近的权重向量wb作为最佳匹配单元。
| $ d = \arg \;\mathop {\min }\limits_{j = 1, L, l} \left\| {{x_i} - {w_j}} \right\| $ | (1) |
(5)以最佳匹配单元为中心,更新最佳匹配单元及邻域范围内的神经元的权重向量,应用更新公式
| $ {w_j}(t + 1) = {w_j}(t) + \eta (t){h_{bj}}(t)\left[ {{x_i} - {w_j}(t)} \right] $ | (2) |
式中:wj (t + 1)为第t + 1次迭代过程中第j个节点的权重向量;η(t)为学习速度参数;hbj (t)为邻域核函数,用来对最佳匹配单元周边的激发向量移动距离进行计算,通常选取高斯函数,即:
| $ {h_{bj}}(t) = \exp \left[ { - \frac{{d_{bj}^2}}{{2\sigma {{(t)}^2}}}} \right] $ | (3) |
式中:σ(t)为第t次迭代过程的邻域半径。
(6)重复步骤(3)-(5),直到算法达到收敛或迭代达到指定的次数,迭代过程终止。
2.2 模糊识别方法传统的SOM分类模式,一旦学习过程完成,使用获胜神经元集合来对集合中的每个多属性样本进行分类。每个样本的类别由其最佳匹配神经元的类别提供。而神经元的类别可以采用“委员会投票法”获得。在这种情况下,可能会造成该神经元局部空间的信息损失,因此,采用模糊系统的相关理论进行局部空间有监督判定准则的校正[18]。
模糊系统是“if-then”规则的集合,这些规则将输入映射到输出,每一条规则将输入的一部分映射到输出的一部分,通常采用隶属度函数定量地描述这种规则。因此,模糊系统通常采用模糊基函数的线性组合来描述,根据Stone-Weierstrass定理,模糊基函数的线性组合总能以任意精度逼近紧致集U上的任意连续势函数[18]。
将在局部神经元空间中的数据点看作是多维欧氏空间的点,根据样品与类中心之间的隶属度进行类型的划分,也即每个样品可以属于任何一个类中心,但是属于每种类可能性不同,即隶属度不一样。通常输入变量的模糊集合的隶属函数采用高斯函数,即:
| $ \mathit{\boldsymbol{U}}_j^k\left( {{x_i}} \right) = \exp \left[ { - \frac{1}{2}{{\left( {\frac{{{x_i} - \mu _j^k}}{{\sigma _j^k}}} \right)}^2}} \right] $ | (4) |
式中:Ujk(xi)为第i个样本第k种特征参数,属于第j种类型的隶属度;μjk为第k种特征参数第j种类型的均值;σjk为第k种特征参数的第j种类型的方差;1 ≤ k ≤ N,1 ≤ j ≤ M,N为测井特征参数个数,M为岩性类型个数。此时,模糊基函数的表达式为
| $ {p_j}\left( {{x_i}} \right) = \frac{{\prod\limits_{i = 1}^N {{\mathit{\boldsymbol{U}}}_j^k} \left( {{x_i}} \right)}}{{\sum\limits_{j = 1}^M {\left[ {\prod\limits_{i = 1}^N {{\mathit{\boldsymbol{U}}}_j^k} \left( {{x_i}} \right)} \right]} }} $ | (5) |
| $ T = \mathop {\max }\limits_{j = 1, 2, \cdots , M} {p_j}\left( {{x_i}} \right) $ | (6) |
式中:pj(xi)为第i个样本属于第j种类型的概率;T为pj(xi)取最大值时对应的岩性类型。
针对研究目标,具体算法如下:
(1)通过前人研究及不同岩性测井参数分析,选择对岩性较为敏感的测井参数[1]。
(2)初始化SOM网络,通过测井参数数据训练SOM网络,根据式(1)计算神经元与测井样本的距离,确定最佳匹配单元,并根据式(2)更新权重。
(3)当SOM网络收敛或者达到指定迭代次数,则训练完成,否则迭代步骤(2)。
(4)通过SOM网络训练过程中,每个样本数据投影到SOM神经元中。根据式(4)计算神经元中每个样本与每种岩性类型之间的隶属度。并通过式(5)得到每个样本属于每种岩性类型的概率。
(5)根据式(6)计算每个样本点的岩性类型,最终得到整个测井的岩性序列。
3 SOM分析过程 3.1 拓扑结构选择在开始使用SOM进行测井相分析时,首先要确定SOM神经元的个数,其个数不同对数据分布的拟合会有不同的效果。SOM分析过程中主要执行“矢量投影”(或称为“拓扑保存”)和“矢量量化”2个过程[19]。为了定量表征SOM拓扑结构的效果,通常采用平均量化误差(Quantization Error,QE)和地形误差(Topographic Error,TE),前者通过计算样本点和最佳匹配单元距离的平均值度量SOM的矢量量化的能力,后者通过计算样本点最佳匹配单元和次优匹配单元是否相邻来衡量拓扑保存的质量。平均量化误差和地形误差计算公式如下
| $ QE = \frac{{\sum\limits_{i = 1}^m d \left( {{x_i} - {w_{\rm{b}}}} \right)}}{m} $ | (7) |
| $ TE = \frac{{\sum\limits_{i = 1}^m \mu \left( {{x_i}} \right)}}{m}, $ |
| $ \mu \left( {{x_i}} \right) = \left\{ \begin{array}{l} 0, 如果最佳和次佳匹配神经元相邻\\ 1, 如果最佳和次佳匹配神经元不相邻 \end{array} \right. $ | (8) |
式中:wb为当前输入样本的最佳匹配单元;d(xi-wb)为当前输入样本与其最佳匹配单元的欧氏距离;μ(xi)为第i个样本的映射函数;m为样本数,个。
通过选择图 1所示的6种测井参数,确定其输入空间的维数为六维,不同的测井参数具有不同的单位,因此,在输入之间需要对其进行归一化处理。通过设置不同的网格大小,采用QE和TE评价SOM不同网格大小的拓扑结构的性能(表 1)。网格数的增加会降低QE,但TE并不随着做线性变化。显然,不同构型的SOM对于原始数据参数空间展布结构的描述不尽相同,并没有一个全面的指标来衡量哪种构型的SOM更能代表原始数据的分布,在本文中使用10×15的SOM进行问题分析。
|
|
下载CSV 表 1 不同网格大小SOM的性能指标值 Table 1 Performance index values of SOM with different size grid |
以往地质工作者仅将SOM作为一种无监督聚类方法或者降维技术来使用,从而忽视其作为一种强大的可视化工具,SOM具有从多种角度为地质工作者展现测井数据在参数空间中的分布情况以及测井参数之间的联系和变化趋势等特征的能力[19]。
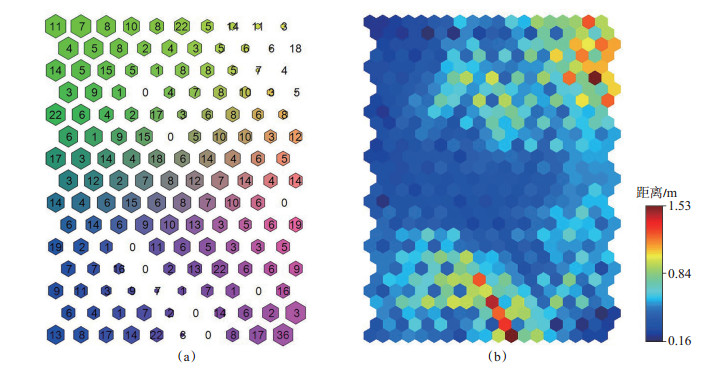
拓扑结构示意图是最基本的可视化技术,图 4(a)是通过研究工区测井数据得到的结果,图中六边形表示采用的神经元的结构,其大小表示该神经元所能激活的范围,数字表示落入到该神经元中样本的数量,颜色表示神经元在拓扑结构中的位置,颜色相近表示位置相邻。从整体上看,网格北西-南东方向(以正上为北)的神经元覆盖更多的数据点和更大的参数空间区域,当地质工作者对某一神经元更感兴趣时,可以对该区域的数据点进行更精细更深层次的描述与刻画。需要特别指出的是,在网格结构中,存在着空白神经元,说明训练数据中缺乏这些神经元所对应的输入模式。
|
下载eps/tif图 图 4 拓扑网络示意图(a)和U矩阵(b) Fig. 4 Sketch map of topology network(a)and U matrix(b) |
为了更好地表征输入样本之间的相似性,计算相邻神经元之间的距离,得到标准化距离矩阵(U矩阵)[8],该距离是通过神经元及其周边多个神经元的距离的平均值得到的,距离矩阵本质上显示了不同部分神经元的密度。因而它不仅能够反映不同神经元之间的距离,还可以展示神经元之间的差异性。对于一个含有10×15个神经元的网络,其矩阵中对应19×29个节点,通过SOM训练,得到如图 4(b)所示的U矩阵,可以明显看出存在着2个类别,暖色区域代表神经元之间的距离较大,数据分布较为分散,冷色部分代表神经元之间的距离较小,数据分布比较紧密,结合数据标签,这两大类对应的是灰岩和白云岩。U矩阵表征了将高维数据投影到二维空间,为下一步的岩心识别和分析提供了初步的认识。
3.3 测井参数拓扑结构分析通过袁照威[20]的研究,识别模型常分为有监督的学习和无监督的学习,但从本质上这2种模型都依赖于不同类型的数据在特征空间中的某种距离度量方式的可分性,一旦距离被定义,那么距离小的样本比较相似,距离大的样本彼此不同[12]。在传统的基于全局欧氏距离的模型范氏下,数据的成簇结构是以某个统计量为中心,以不同类别的该统计量的距离的某个分位点为半径的超球体结构呈现的,例如K-means方法的聚类中心和聚类半径,贝叶斯推断中高斯函数的均值和方差等,这些无序的超球体填充在数据的分布空间中,直接构成了样本的分类空间,但数据的本征维度是否是欧式空间,数据流形是否符合实验者的假设却往往不得而知。
SOM的有序输出,能够为此类问题提供另一种解决思路。实际上,SOM的训练可以看做是探究二维平面在欧式空间中的卷曲情况,从外蕴空间(欧式空间)的坐标倒推内蕴空间(拓扑空间)的坐标的过程[19]。如图 5(a)所示,红框圈出来的区域分别是117号神经元(团)和150号神经元(团),这2团神经元在欧氏距离度量下较接近,如5(b)所示,这2团神经元映射着不同标签的样本(红色样本代表灰岩,绿色样本代表白云质灰岩),在映射完成后,SOM隐式的执行了一种“展开”操作,即在2 D平面内,117号神经元(团)和150号神经元(团)彼此远离,至此,SOM完成了对于嵌在高位欧式空间下的二维流形的挖掘,有序的输出结构将数据本身的流形结构得以恢复,经过这种映射,一种新的距离取代了欧氏距离,衡量了2类样本的相似性。同类别数据更接近,而不同类别的数据更加远离。同时,SOM训练完毕后,每个神经元形成独立的局部空间,同时相比全局空间,依据局部空间的光滑性,可以假定该空间为欧式空间。这也为后续的有监督微调局部空间判别准则提供了依据。

|
下载eps/tif图 图 5 二维拓扑结构在三维数据空间中的折叠(a)及与训练数据的叠合图(b) Fig. 5 2-D topological structure(a)and train data(b)fold in 3-D data space |
为了说明算法的应用效果,以苏里格气田苏东41-33区块W1井为例,选择自然伽马、密度、光电截面吸收指数、补偿中子、声波时差、深侧向电阻率等6种测井特征参数,也即上述算法中N = 6,M = 7。首先结合专家信息和岩屑测录井资料,对该区域部分特征明显的样本进行岩性标定,然后将有岩性类型的测井参数样本数据作为算法输入训练SOM模型,训练完毕后,每个神经元都会形成一个局部空间,使用该区域内带有标记的样本建立模糊系统,使用公式求取待测样本对于每一个类型的概率,最后选择概率最大的类别作为该样本的最终类别,得到最终的岩性识别结果,同时采用传统的模糊识别方法作为对比方法,并与测录井资料进行对比分析。
从定性角度看出,本文方法得到的岩性识别结果和钻录井岩心得到的结果整体上表现出一致的特征,而模糊识别方法则存在很大的差异(图 6)。在3 431.8~3 435.4 m井段处,本文方法得到的灰质白云岩,而模糊识别则识别为泥质白云岩,在其他深度处也存在一定的误判现象。这进一步说明了所选择的特征在欧式空间相近,但在拓扑空间中得到“展开”,这样得到的结果就存在一定的差异。

|
下载eps/tif图 图 6 W1井岩性识别结果 Fig. 6 Lithology identification result of well W1 |
通过统计不同方法的混淆矩阵,定量得到不同方法的识别精度(表 2)。使用本文提出的基于SOM和模糊识别的方法对该工区W1井的所有样本点进行测试,最终的准确率为87.9%,而在全局空间使用传统的模糊识别方法的准确率为80.6%,准确率提高了7.3%。
|
|
下载CSV 表 2 不同岩性识别方法混淆矩阵 Table 2 Confusion matrix of different lithology identification methods |
(1)自组织映射模型能够反映测井参数之间的相关性,挖掘数据中的典型模型,将高维变量映射到二维平面上,利用多种可视化手段展示出中间过程,便于和地质工作者的经验相结合。
(2)SOM作为拓扑学习的典型代表,可以捕捉到数据的局部邻域信息和整体变化趋势,通过和专家信息的有效结合,在局部空间使用模糊识别方法调整分类策略。
(3)通过全局无监督学习和局部有监督分类相结合的方法,得到更符合实际岩性的识别结果,与传统的模糊识别方法相比,识别正确率得到大幅度提高。
(4)“全局无监督拓扑学习+局部有监督分类”具有可行性和有效性,为地质人员在储层评价过程中提供了一种新的解决方法和思路。
| [1] |
袁照威, 段正军, 张春雨, 等. 基于马尔科夫概率模型的碳酸盐岩储集层测井岩性解释. 新疆石油地质, 2017, 38(1): 96-102. YUAN Z W, DUAN Z J, ZHANG C Y, et al. Interpretation of logging lithology in carbonate reservoirs based on Markov Chain probability model. Xinjiang Petroleum Geology, 2017, 38(1): 96-102. |
| [2] |
吴磊, 徐怀民, 季汉成. 基于交会图和多元统计法的神经网络技术在火山岩识别中的应用. 石油地球物理勘探, 2006, 41(1): 81-86. WU L, XU H M, JI H C. Application of neural network based on crossplot and multivariate statistical method in identification of volcanic rocks. Oil Geophysical Prospecting, 2006, 41(1): 81-86. DOI:10.3321/j.issn:1000-7210.2006.01.016 |
| [3] |
马峥, 张春雷, 高世臣. 主成分分析与模糊识别在岩性识别中的应用. 岩性油气藏, 2017, 29(5): 127-133. MA Z, ZHANG C L, GAO S C. Lithology identification based on principal component analysis and fuzzy recognition. Lithologic Reservoirs, 2017, 29(5): 127-133. DOI:10.3969/j.issn.1673-8926.2017.05.015 |
| [4] |
MA Y Z. Lithofacies clustering using principal component analysis and neural network:Applications to wireline logs. Mathematical Geosciences, 2011, 43(4): 401-419. DOI:10.1007/s11004-011-9335-8 |
| [5] |
WANG G C, CARR T R, JU Y W, et al. Identifying organicrich marcellus shale lithofacies by support vector machine classifier in the Appalachian Basin. Computers & Geosciences, 2014, 64(3): 52-60. |
| [6] |
CHANG H C, KOPASKA-MERKEL D C, CHEN H C, et al. Lithofacies identification using multiple adaptive resonance theory neural networks and group decision expert system. Computers & Geosciences, 2000, 26(5): 591-601. |
| [7] |
单敬福, 陈欣欣, 赵忠军, 等. 利用BP神经网络法对致密砂岩气藏储集层复杂岩性的识别. 地球物理学进展, 2015, 30(3): 1257-1263. SHAN J F, CHEN X X, ZHAO Z J, et al. Identification of complex lithology for tight sandstone gas reservoirs sase on BP neural net. Progress in Geophysics, 2015, 30(3): 1257-1263. |
| [8] |
VILALMANN T. Topology preservation in self-organizing maps. Kohonen Maps, 1999, 27(2): 279-292. |
| [9] |
FRASER S J, DICKSON B L. A new method for data integration and integrated data interpretation: Self-organizing maps//MILKEREIT B. Proceedings of exploration 07: Fifth decennial international conference on mineral exploration. Torouto: Decennial Mineral Exploration Conference Publisher, 2007: 907-910.
|
| [10] |
许少华, 何新贵, 李盼池. 自组织过程神经网络及其应用研究. 计算机研究与发展, 2003, 40(11): 1612-1615. XU S H, HE X G, LI P C. Research and applications of self-organization process neural networks. Journal of Computer Research and Development, 2003, 40(11): 1612-1615. |
| [11] |
KOHONEN T. Self-organized formation of topologically correct feature maps. Biological Cybernetics, 1982, 43(1): 59-69. DOI:10.1007/BF00337288 |
| [12] |
ROY A, MATOS M, MARFURT K J. Automatic seismic facies classification with Kohonen self organizing maps-a tutorial. Geohorizons, 2010, 1(1): 6-14. |
| [13] |
韩波, 何治亮, 任娜娜. 四川盆地东缘龙王庙组碳酸盐岩储层特征及主控因素. 岩性油气藏, 2018, 30(1): 75-85. HAN B, HE Z L, REN N N. Characteristics and main controlling factors of carbonate reservoirs of Longwangmiao Formation in eastern Sichuan Basin. Lithologic Reservoirs, 2018, 30(1): 75-85. DOI:10.3969/j.issn.1673-8926.2018.01.008 |
| [14] |
田亮, 李佳玲, 焦保雷. 塔河油田12区奥陶系油藏溶洞充填机理及挖潜方向. 岩性油气藏, 2018, 30(3): 52-60. TIAN L, LI J L, JIAO B L. Filling mechanism and potential tapping direction of Ordovician karst reservoirs in block-12 of Tahe Oilfield. Lithologic Reservoirs, 2018, 30(3): 52-60. |
| [15] |
张 䶮, 郑晓东, 李劲松, 等. 基于SOM和PSO的非监督地震相分析技术. 地球物理学报, 2015, 58(9): 3412-3423. ZHANG Y, ZHENG X D, LI J S, et al. Unsupervised seismic facies analysis technology based on SOM and PSO. Chinese Hournal of Geophysics, 2015, 58(9): 3412-3423. |
| [16] |
段林娣, 张春雷, 王利田, 等. 储层建模新技术、新方法研究:基于模糊系统的储层建模方法. 内蒙古石油化工, 2007, 32(4): 76-79. DUAN L D, ZHANG C L, WANG L T, et al. Research on reservoir model ing based on fuzzy system. Inner Mongolia Petrochemical Industry, 2007, 32(4): 76-79. DOI:10.3969/j.issn.1006-7981.2007.04.047 |
| [17] |
RITTER H, MARTINETZ T, SCHULTEN K, et al. Neural computation and self-organizing maps:an introduction. Boston: Addison-Wesley, 1993: 243-244.
|
| [18] |
KOSKO B. Fuzzy engineering. Upper Saddle River, NJ: Prentice Hall, 1996: 35-75.
|
| [19] |
VESANTO J, AHOLA J. Hunting for correlations in data using the self-organizing map//ROCHESTER N Y. Proceedings of the international ICSC congress on Computational Intelligence Methods and Applications(CIMA'99). Switzerland: ICSC Academic Press, 1999: 279-285.
|
| [20] |
袁照威.基于机器学习与多信息融合的致密砂岩储层井震解释方法研究.北京: 中国地质大学(北京), 2017. YUAN Z W. Interpretation methods of tseight sandstone reservoir with seismic data and welllogs based on machine learning method and multi-information fusion. Beijing: China University of Geosciences(Beijing), 2017. http://cdmd.cnki.com.cn/Article/CDMD-11415-1017126056.htm |
 2019, Vol. 31
2019, Vol. 31



