2. 成都理工大学 地球物理学院, 成都 610059
2. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
随机噪声压制是地震资料处理的关键环节之一[1]。Anvari等[2]将常用的地震信号去噪方法分为4类:①预测滤波。基于时空域或变换域中有效信号是可预测的,而随机噪声不可预测,如t-x域预测滤波[3]、f-x域反褶积[4]。②中值滤波。该类方法以信号和随机噪声的统计规律不同为基础,包括时变中值滤波[5]和矢量中值滤波[6]等方法。③基于信号相干性的随机噪声压制方法,如各向异性扩散滤波[7],字典学习[8]等。④基于信号分解的去噪方法,如经验模态分解[9]、奇异值分解[10]、稀疏表示[11-12]等。其中稀疏表示是一种现行有效的随机噪声压制方法,该方法认为地震数据是可压缩的,在某一字典下有效信号能够获得最佳的稀疏表示,而随机噪声与有效信号不同源,同一字典下不能实现有效的稀疏表示。因此,字典的有效性就决定了稀疏表示算法的去噪能力。根据构建方法的不同,常用的字典分为:①分析型字典。由数学基函数构建而成,如Fourier字典、Morlet小波字典、Curvelet字典和Ricker子波字典等,实际应用中,这类字典常难以精确描述地震信号特征。②字典学习。这类方法是数据驱动下的地震去噪,优点是具有自适应性,但该类方法缺点是计算成本高。③地震物理子波构建子波字典。该方法由地震资料提取统计子波或结合井震资料提取子波,构建字典,能够有效描述地震信号特征[12],物理意义明确,且计算效率高。
稀疏表示算法的核心思想是使用少量的基函数就能实现信号的有效表示,揭示信号的本质特征[13]。被广泛应用于地震数据分析,如地震数据采集[14]、去噪[12]、重建[15]、最小二乘偏移[16]和反射系数反演[17]等领域。受压缩感知[18-19]、线性表示及相关数学理论研究成果的促进,国内外学者[20-22]提出了一系列稀疏表示算法。Zhang等[13]将其分为为4类:贪婪算法[20]、约束优化算法[21-22]、同伦算法[23]和临近算法[24]。这些算法均以单测量模型(Single Measurement Vector,SMV)为基础,多采用L1范数正则项,仅适用于一维信号稀疏表示[25]。受阵列信号处理需求推动,Cotter等[25]提出了基于多测量模型(Multiple Measurement Vector,MMV)的联合稀疏表示(Joint Sparse Representation),采用L2,1范数正则项,在同一支撑下,参与计算的各道信号同时获得最优稀疏表示,并指出采用MMV模型能够放松解唯一性条件的上界。Eldar等[26]证明重建精度与测量矢量数成指数相关。Jin等[27]也证实了MMV模型能够显著提高信号重建精度。然而,联合稀疏表示是一个非确定性多项式(Nondeterministic Polynomial-time,NP)问题,计算效率是制约该算法应用于地球物理数据处理的瓶颈。交替方向乘子法(Alternating Direction Method of Multipliers,ADMM)是公认为计算效率最高的优化方法,能够适用于大尺度数据优化处理[21]。Yang等[21]证明了ADMM算法的收敛性,提出一种基于ADMM的联合稀疏表示算法,并证实具有优越的计算效率。
传统基于稀疏表示的地震数据去噪方法均采用一维算法逐道处理,无法有效利用信号的空间相干性,道集内各地震道的去噪处理是相互独立的,处理结果一致性较差,去噪的同时会损害有效波,而叠前共偏移距道集中各波形均为水平同相轴,满足联合稀疏表示的共稀疏性(Common Sparsity)假设条件,可采用联合稀疏表示对该道集中各地震道同时进行稀疏分解。针对上述问题,提出基于联合稀疏表示的共偏移距道集随机噪声压制方法,利用地震资料提取子波作为基函数,构造子波字典,再利用基于ADMM的联合稀疏表示对共偏移距道集进行去噪处理,以期兼顾有效信号的道间相干性和空间变化,达到压制噪声的同时还能够保持有效信号不被损害的目的。
1 方法原理随着重点勘探领域由构造油气藏向深层岩性、地层等复杂油气藏转变,勘探开发研究更加依赖高保真地震数据,对随机噪声压制处理提出了更高的要求。传统的一维稀疏表示去噪方法受多解性和单道处理方法局限性的制约,难以兼顾地震道间相干性和信号空间变化。共偏移距道集具有水平同相轴结构,表现出良好的空间相干性,满足共稀疏性假设条件,而随机噪声空间分布不规律,将联合稀疏表示用于叠前共偏移距道集就能提高去噪处理的有效性。
1.1 共偏移距道集联合稀疏去噪方法稀疏表示去噪方法以层状介质模型为基础,地震记录满足褶积模型
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Wr}} $ | (1) |
式中:s为地震道;r为地下介质的单位冲击响应;W为子波核矩阵(1.3节将详述其构建方法)。
有效地震信号和随机噪声由不同的场源产生,因此有效信号能够被子波核矩阵W充分表示,而噪声与反射信号不同源,在同一组基函数下不能获得有效表示,成为稀疏表示残差。如果以W为字典,利用稀疏表示算法对地震道s进行稀疏表示,再由稀疏表示结果r重构出地震记录s*,就能实现信号和噪声分离。传统算法常采用基追踪(Basis Pursuit,BP)对地震道进行稀疏分解,目标函数为
| $ \mathop {\min }\limits_r \left\{ {{{\left\| \mathit{\boldsymbol{r}} \right\|}_1}+\lambda {{\left\| {\mathit{\boldsymbol{Wr}}-\mathit{\boldsymbol{s}}} \right\|}_2}} \right\} $ | (2) |
式中:λ > 0为参数;||·||1为L1范数;||·||2为L2范数。
目标函数式(2)采用L1范数正则项实现稀疏约束,反演出单位冲激序列r由少量的大反射脉冲和呈Gaussian分布的小反射脉冲组成,这也与实际的地层结构相吻合。该方法为一维去噪算法,逐道处理地震数据,没有利用有效信号的空间相干性。同时算法受多解性影响,稀疏表示结果只是满足条件的一个实例,相邻地震道较小的变化可能会引起稀疏表示结果和重构信号较大的区别,造成处理结果一致性较差,去噪同时会损害有效波。
针对一维算法的不足,受阵列信号处理启发,将联合稀疏表示算法用于共偏移距道集地震数据去噪处理,其目标函数为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{R}} \left\{ {{{\left\| \mathit{\boldsymbol{R}} \right\|}_{2, 1}}+\lambda {{\left\| {\mathit{\boldsymbol{WR}}-\mathit{\boldsymbol{S}}} \right\|}_F}} \right\} $ | (3) |
式中:S为共偏移距道集,每一列表示一个地震道;R为单位冲击响应矩阵;||·||2, 1为L2,1范数;||·||F为Frobenius范数。
采用L2,1范数正则项实现共稀疏性约束,反演结果R仅有少量大反射脉冲行。
当信号中混有异常值时,采用Frobenius范数拟合项会放大异常值的影响,容易造成算法不稳定,从而导致算法不收敛或收敛到局部次优解。采用L2,1范数拟合项代替式(3)中的Frobenius范数,构造出一种稳健的L2,1-L2,1范数稀疏表示方法,其目标函数为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{R}} \left\{ {{{\left\| \mathit{\boldsymbol{R}} \right\|}_{2, 1}}+\lambda {{\left\| {\mathit{\boldsymbol{WR}}-\mathit{\boldsymbol{S}}} \right\|}_{2, 1}}} \right\} $ | (4) |
L2,1-L2,1范数稀疏表示的目标函数由一个L2,1范数正则项和一个L2,1范数拟合项构成,因此,式(4)是一个非平滑凸函数,难以直接迭代优化。求解思路是:通过变量代换和组合,将目标函数式(4)转化为一个等价联合基追踪(Joint Basis Pursuit)问题,然后通过ADMM算法进行迭代优化。基于ADMM的L2,1-L2,1范数稀疏表示算法描述如下:
令
| $ \mathop {\min }\limits_\mathit{\boldsymbol{R}} {\left\| {\mathit{\boldsymbol{\hat R}}} \right\|_{2, 1}}\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\mathit{\boldsymbol{\hat W\hat R}} = \mathit{\boldsymbol{\hat S}} $ | (5) |
引入任意变量Z =Ȓ,将目标函数式(5)转化为
| $ \mathop {\min }\limits_{\mathit{\boldsymbol{\hat R}}, \mathit{\boldsymbol{Z}}} {\left\| {\mathit{\boldsymbol{\hat R}}} \right\|_{2, 1}}\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\mathit{\boldsymbol{\hat W\hat R}} = \mathit{\boldsymbol{\hat S}}, \;\mathit{\boldsymbol{\hat R}} = \mathit{\boldsymbol{Z}} $ | (6) |
可以看出,式(6)是变量可分离的,可用ADMM进行优化处理,其增广Lagrange函数如下
| $ \begin{array}{*{20}{c}} {\mathop {\min }\limits_{\mathit{\boldsymbol{\hat R}}, \mathit{\boldsymbol{Z}}} \left\{ {{{\left\| {\mathit{\boldsymbol{\hat R}}} \right\|}_{2, 1}}-{\mathit{\Lambda }_1}(Z-\mathit{\boldsymbol{\hat R}})+\frac{{{\beta _1}}}{2} < Z, \mathit{\boldsymbol{\hat R}} > -} \right.}\\ {\left. {{\mathit{\Lambda }_2}(\mathit{\boldsymbol{\hat W\hat R}}-\mathit{\boldsymbol{\hat S}})+\frac{{{\beta _2}}}{2} < \mathit{\boldsymbol{\hat W\hat R}}, \mathit{\boldsymbol{\hat S}} > } \right\}} \end{array} $ | (7) |
式中:Λ1和Λ2均为Lagrange乘子;β1和β2均为惩罚参数。
应用ADMM算法优化式(7),得到如下迭代公式
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{\hat R}} \leftarrow {{\left( {{\beta _1}\mathit{\boldsymbol{I}}+{\beta _2}{\mathit{\boldsymbol{W}}^T}\mathit{\boldsymbol{W}}} \right)}^{-1}}\left( {{\beta _1}\mathit{\boldsymbol{Z}}-{\mathit{\Lambda }_1}+{\beta _2}{\mathit{\boldsymbol{W}}^T}\mathit{\boldsymbol{\hat S}}+{\mathit{\boldsymbol{W}}^T}{\mathit{\Lambda }_2}} \right)}\\ {\mathit{\boldsymbol{Z}} \leftarrow Row\_Shrink\left( {\mathit{\boldsymbol{\hat R}}{\rm{+}}\frac{{\rm{1}}}{{{\beta _{\rm{1}}}}}{\mathit{\Lambda }_{\rm{1}}}, \frac{{\rm{1}}}{{{\beta _{\rm{1}}}}}} \right)}\\ {{\mathit{\Lambda }_1} \leftarrow {\mathit{\Lambda }_1}-{\gamma _1}{\beta _1}(\mathit{\boldsymbol{Z}}-\mathit{\boldsymbol{\hat R}})}\\ {{\mathit{\Lambda }_2} \leftarrow {\mathit{\Lambda }_2}-{\gamma _2}{\beta _2}(\hat W\mathit{\boldsymbol{\hat R}}-\mathit{\boldsymbol{\hat S}})} \end{array}} \right. $ | (8) |
式中:Row_Shrink(·,·)为组迭代收缩阈值算子;γ1和γ2均为迭代步长。
1.3 字典构造方法字典的优劣决定了去噪算法的性能[12],要求字典的原子能够精确描述地震记录。由地震资料提取的地震子波具有明确的物理意义,符合地震波场规律,能够有效地描述地震信号,满足稀疏表示方法需要。用地震子波构造字典对地震信号进行稀疏分解。
基本的单子波字典构建流程如下:
(1)由地震资料提取地震子波w;
(2)构造子波字典为一个Toeplitz矩阵,其第(i,j)元素为Wij = wi-j+1(式中:wi-j+1为子波w的第i-j+1个元素);
(3)对字典的每一列做归一化处理。
地震记录不是稳态信号,其振幅、相位随着时间、空间发生变化,因此地震子波也是时变和空变的。Edgar等[28]、冯玮等[29]的研究结果表明,子波的微小变化会对处理、解释结果产生较大影响。随着油气藏勘探开发难度的增加,采用单子波构造字典常难以满足生产需求,可以采用时变子波[29]、空变子波[30]构造字典,或由多子波字典串联[12]构造字典。当研究薄层储层预测时,可以利用双极子分解[16, 31-33]构造过完备楔形子波字典对地震记录进行稀疏分解。
2 数值模拟通过数值模拟验证所提基于联合稀疏表示的共偏移距道集随机噪声压制方法的有效性,设计一个5层地质模型[图 1(a)],地层速度分别为:2 000 m/s,2 300 m/s,2 200 m/s,2 400 m/s和2 200 m/s;界面埋深分别为:200 m,400 m,600 m和800 m。地震正演采用30 Hz雷克子波,采用中间放炮两边接收观测系统,道间距和最小炮检距均为50 m,每炮48道接收。从正演地震记录[图 1(b)]可以看出,受地质构造和观测系统影响,叠前共炮点道集中反射波同相轴具有双曲线特征,不同深度地层反射波同相轴倾角不同。因此,共炮点道集不满足联合稀疏表示的共稀疏性假设,不能直接应用联合稀疏表示去噪方法。为了验证算法的噪声鲁棒性和有效性,对正演地震数据混入随机噪声和异常值,加噪共炮点道集[图 1(c)],信噪比为10 dB。抽取50 m共偏移距道集[图 1(d)],图中各反射波均为水平同相轴,各道中同一界面的反射波出现时间相同,满足联合稀疏表示的共稀疏性假设。因此,可以采用联合稀疏表示在该道集中进行去噪处理。

|
下载eps/tif图 图 1 地质模型和地震正演 Fig. 1 Geological model and seismic forward modeling |
图 2展示了基于联合稀疏表示的共偏移距道集去噪结果。实验中取λ = 0.4,其中图 2(a)为处理后50 m共偏移距道集,与图 1(d)对比可以发现,处理后随机噪声得到压制,信噪比提高3.074 dB。图 2(b)为共偏移距道集残差,滤波残差呈随机噪声分布规律,说明去除随机噪声的同时没有损害有效波。处理后,再由共偏移距道集抽取共炮点道集,图 2(c),(d)分别为第1炮去噪结果和滤波残差,处理后剖面信噪比提高到3.105 dB,随机噪声得到有效压制,残差剖面呈随机噪声分布规律,无有效波泄露。说明信号与噪声不同源,以地震子波为基函数,反射信号能够被有效表示,而噪声不能。同时,共偏移距道集中,联合稀疏表示能够有效利用信号空间的相干性,提高处理效果。

|
下载eps/tif图 图 2 共偏移距道集联合稀疏表示去噪结果 Fig. 2 De-noise based on joint sparse representation in common offset gathers |
为了突出共偏移距道集去噪方法的优越性,对比了传统的基于一维信号稀疏表示的单道去噪方法(图 3)。与图 2实验相同,取λ = 0.4。图 3(a)为第1炮经传统的单道算法处理后剖面,虽然处理后随机噪声得到压制,但信噪比提高有限,仅为0.849 dB。图 3(b)为第1炮滤波残差,剖面上呈现明显的双曲线同相轴特征(图中箭头所示),说明单道处理算法不能有效利用信号的空间相干性,同时受多解性干扰,去噪同时会损害有效波。

|
下载eps/tif图 图 3 第1炮一维算法单道处理结果 Fig. 3 Processing results of the first shot gather based on 1-D algorithm in trace-by-trace mode |
为了进一步说明所提算法的优越性,以第1炮第24道为例,对比2种算法处理结果(图 4)。图 4(a)和(b)分别为第24道正演地震记录和加噪信号。图 4(c)为传统算法处理结果,图 4(d)为共偏移距道集中联合稀疏表示算法处理结果,对比2种算法处理结果可以看出,2种算法都能有效压制随机噪声,处理后信噪比分别提升0.986 dB和2.781 dB,说明共偏移距道集算法具有更好的去噪效果。图 4(e)为传统算法滤波残差,与图 4(a)和(b)对比发现,残差中出现明显的反射信号(图中箭头所示),与原始信号及加噪信号相似度高,说明有效信号被压制。图 4(f)为共偏移距道集滤波残差,呈现随机噪声分布特征,说明去噪同时没有损害有效波。分析结果说明,所提的共偏移距道集联合稀疏表示算法具有明显优势。

|
下载eps/tif图 图 4 第24道地震信号2种去噪方法对比分析 Fig. 4 Comparative analysis of two de-noising methods for the 24 th seismic trace |
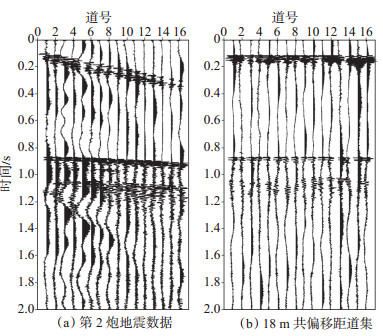
受采集因素制约,地震信号常混有随机噪声,而稀疏表示方法是一个病态的逆问题,噪声和异常值会影响算法的稳定性。要求去噪方法具有较好的噪声鲁棒性,适应信号的空间变化规律,去噪同时不损害有效波。为了验证共偏移距道集中联合稀疏表示去噪方法的有效性,以开放数据White Sea Line 5(数据由俄罗斯Deco Geophysical Software CO.提供)为例进行试算。由地震数据提取统计子波构造子波字典,对传统单道处理和共偏移距道集联合稀疏表示2种去噪方法进行对比分析。图 5(a)为第2炮地震数据,该数据受随机噪声和涌浪噪声干扰严重,处理前必须对地震噪声进行压制。同时剖面上反射波为双曲线同相轴,直达波时距曲线为直线,不同地层时距曲线斜率不同,互相干涉叠加,随机噪声压制困难。图 5(b)为18 m共偏移距道集,剖面各波形均为水平同相轴,各反射波双程旅行时相同,满足联合稀疏表示共稀疏性假设,信号与噪声分布特征不同,有利于联合稀疏表示算法进行去噪处理。因此,该道集中进行联合稀疏表示压制随机噪声,能够有效挖掘地震数据的空间相干性,降低算法的多解性,提高算法的去噪性能。
|
下载eps/tif图 图 5 原始地震数据 Fig. 5 Raw seismic section |
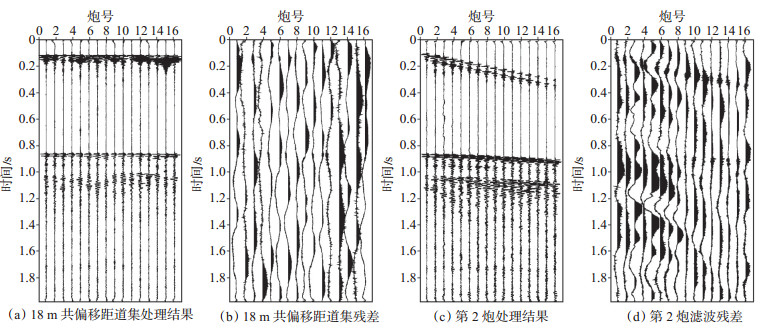
图 6为共偏移距道集中联合稀疏表示去噪结果。其中图 6(a)为共偏移距道集去噪结果,处理后信噪比提高4.364 dB。图 6(c)为去噪后第2炮,处理后信噪比提高3.972 dB,与图 5(a)和(b)比对可以看出,处理后道集同相轴连续性得到增强,随机噪声和涌浪噪声被抑制。图 6(b)和(d)分别为共偏移距道集和炮集滤波残差,剖面符合随机噪声分布规律,说明该方法能够有效利用信号、噪声空间分布特征的区别,多道数据同时参与计算,相当于增加约束条件,缩小解空间,减小多解性,准确反演出地下地层单位冲激响应,再由子波字典重构出地震记录,就能较好地实现信噪分离。
|
下载eps/tif图 图 6 共偏移距道集联合稀疏表示去噪方法实例分析 Fig. 6 Case study of seismic de-noise based on joint sparse representation in common offset gathers |
图 7为传统单道去噪算法处理结果。图 7(a)处理结果的信噪比提高2.397 dB,与图 5(a)对比可以看出,去噪后剖面上同相轴连续性得到一定程度的增强,噪声水平降低。同时,噪声也降低了单道算法的鲁棒性,重建信号存在误差,如图中箭头所示。图 7(b)为滤波残差,剖面上存在明显的连续同相轴(图中箭头所示),说明传统算法去噪同时会损害有效波。其原因是,稀疏表示算法具有多解性,地震噪声会降低算法鲁棒性,使算法难以收敛到最优解,子波字典表示地震信号的能力降低。同时,单道处理方法不能利用有效信号的空间相干性对稀疏表示算法进行约束,与联合稀疏表示算法相比,其计算结果的准确度必然要降低。

|
下载eps/tif图 图 7 传统单道去噪算法实例分析 Fig. 7 Case study of seismic de-noise based on 1-D algorithm in trace-by-trace mode |
图 8以第8道地震信号为例进一步对2种算法进行定性分析。图 8(a)为原始地震道,信号同时受涌浪噪声和随机噪声干扰。由于资料未振幅补偿,深层地震信号能量弱,信噪分离困难。图 8(b)和(c)分别为传统算法、共偏移距道集中联合稀疏表示算法去噪结果,处理后资料信噪比分别提高2.263 dB和3.544 dB。图 8(d)和(e)分别为2种算法滤波残差。对比2种算法处理结果和残差可以发现,受多解性和单道算法局限性制约,传统算法去噪的同时会损害有效波,残差与原始信号及处理后信号相似度较高[图 8(b)和(d)中红色箭头所示]。同时单道算法噪声鲁棒性不好,重建信号失真[图 8(b)中黑色箭头所示],而共偏移距道集中联合稀疏表示算法能够有效利用信号空间相干性,实现有效信噪分离,滤波残差满足随机噪声分布规律,与原始信号、处理后信号不相干[图 8(c)和(e)中红色箭头所示]。

|
下载eps/tif图 图 8 第8道信号2种去噪方法对比分析 Fig. 8 Comparative analysis of two de-noising methods for the 8 th seismic trace |
(1)在共偏移距道集中采用联合稀疏表示压制随机噪声的方法,是基于共偏移距道集中各波形均为水平同相轴,满足联合稀疏表示的共稀疏性假设条件。该道集中联合稀疏表示算法能够兼顾地震道间的相干性和信号空间变化,提高去噪性能。
(2)地震信号常同时混有随机噪声和异常值,采用L2,1范数拟合项能够有效提高算法的鲁棒性,使随机噪声压制方法稳定可靠。L2,1-L2,1范数联合稀疏表示需要采用变量代换和组合将其转换为等价基追踪问题,再通过ADMM进行优化求解,大规模数据处理时需要考虑其计算效率。
(3)稀疏表示算法去噪能力取决于字典性能。地震资料提取地震子波物理意义明确,满足地震波场规律。由地震子波构建字典能够有效描述地震信号,提高去噪能力。当研究区有测井资料时,可以采用井震联合提取地震子波。
(4)地震子波是空间变化的,当研究区采集条件或地下地质条件存在较大变化时,可以考虑采用时变子波或多子波构建子波字典。针对薄储层研究中反射信号弱、噪声污染严重的问题,可以采用双极子分解构建楔形子波字典,提高去噪性能。
| [1] |
王西文, 雍学善, 王宇超, 等. 面对重点勘探领域的地震技术研究和应用实效. 岩性油气藏, 2010, 22(3): 83-90. WANG X W, YONG X S, WANG Y C, et al. Study and application of seismic technologies for key exploration fields. Lithologic Reservoirs, 2010, 22(3): 83-90. DOI:10.3969/j.issn.1673-8926.2010.03.016 |
| [2] |
ANVARI R, SIAHSAR M A N, GHOLTASHI S, et al. Seismic random noise attenuation using synchro squeezed wavelet transform and low-rank signal matrix approximation. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(11): 6574-6581. DOI:10.1109/TGRS.2017.2730228 |
| [3] |
ABMA R, CLAERBOUT J. Lateral prediction for noise attenuation by t-x and f-x techniques. Geophysics, 1995, 60(6): 1887-1896. DOI:10.1190/1.1443920 |
| [4] |
CANALES L L. Random noise reduction. SEG Technical Program Expanded Abstracts, 1984, 525-527. |
| [5] |
LIU Y, LIU C, WANG D. A 1 D time-varying median filter for seismic random, spike-like noise elimination. Geophysics, 2008, 74(1): V17-V24. |
| [6] |
LIU Y K. Noise reduction by vector median filtering. Geophysics, 2013, 78(3): V79-V87. DOI:10.1190/geo2012-0232.1 |
| [7] |
陈可洋, 吴沛熹, 杨微. 扩散滤波方法在地震资料处理中的应用研究. 岩性油气藏, 2014, 26(1): 117-122. CHEN K Y, WU P X, YANG W. Application of diffusion filtering method to the seismic data processing. Lithologic Reservoirs, 2014, 26(1): 117-122. DOI:10.3969/j.issn.1673-8926.2014.01.020 |
| [8] |
CHEN Y K. Fast dictionary learning for noise attenuation of multidimensional seismic data. Geophysical Journal International, 2017, 209(1): 21-31. |
| [9] |
HAN J, VAN DER BAAN M. Microseismic and seismic denoising via ensemble empirical mode decomposition and adaptive thresholding Denoising via EEMD. Geophysics, 2015, 80(6): S69-S80. DOI:10.1190/geo2014-0423.1 |
| [10] |
KREIMER N, SACCHI M D. A tensor higher-order singular value decomposition for prestack seismic data noise reduction and interpolation. Geophysics, 2012, 77(3): V113-V122. DOI:10.1190/geo2011-0399.1 |
| [11] |
CHEN Y K, MA J W, FOMEL S. Double-sparsity dictionary for seismic noise attenuation. Geophysics, 2016, 81(2): V103-V116. DOI:10.1190/geo2014-0525.1 |
| [12] |
DENG L, YUAN S Y, WANG S X. Sparse Bayesian learningbased seismic denoise by using physical wavelet as basis functions. IEEE Geoscience and Remote Sensing Letters, 2017, 14(11): 1993-1997. DOI:10.1109/LGRS.2017.2745564 |
| [13] |
ZHANG Z, XU Y, YANG J, et al. A survey of sparse representation:Algorithms and applications. IEEE Access, 2015, 3: 490-530. DOI:10.1109/ACCESS.2015.2430359 |
| [14] |
MANSOUR H, WASON H, LIN T T Y, et al. Randomized marine acquisition with compressive sampling matrices. Geophysical Prospecting, 2012, 60(4): 648-662. DOI:10.1111/j.1365-2478.2012.01075.x |
| [15] |
MANSOUR H, HERRMANN F J, YILMAZ Ö. Improved wavefield reconstruction from randomized sampling via weighted onenorm minimization. Geophysics, 2013, 78(5): V193-V206. DOI:10.1190/geo2012-0383.1 |
| [16] |
HERRMANN F J, LI X. Efficient least-squares imaging with sparsity promotion and compressive sensing. Geophysical Prospecting, 2012, 60(4): 696-712. DOI:10.1111/j.1365-2478.2011.01041.x |
| [17] |
ZHANG R, CASTAGNA J. Seismic sparse-layer reflectivity inversion using basis pursuit decomposition. Geophysics, 2011, 76(6): R147-R158. DOI:10.1190/geo2011-0103.1 |
| [18] |
DONOHO D L. Compressed sensing. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [19] |
许志强. 压缩感知. 中国科学:数学, 2012, 42(9): 865-877. XU Z Q. Compressed sensing:a survey. Scientia Sinica Mathematica, 2012, 42(9): 865-877. |
| [20] |
CAI T T, WANG L. Orthogonal matching pursuit for sparse signal recovery with noise. IEEE Transactions on Information Theory, 2011, 57(7): 4680-4688. DOI:10.1109/TIT.2011.2146090 |
| [21] |
YANG J F, ZHANG Y. Alternating direction algorithms for l1-problems in compressive sensing. SIAM Journal on Scientific Computing, 2011, 33(1): 250-278. DOI:10.1137/090777761 |
| [22] |
DENG W, YIN W T, ZHANG Y. Group sparse optimization by alternating direction method. Proceedings of SPIE, 2013, 8858. |
| [23] |
PRESNELL B, TURLACH B A, OSBORNE M R. A new approach to variable selection in least squares problems. IMA Journal of Numerical Analysis, 2000, 20(3): 389-403. DOI:10.1093/imanum/20.3.389 |
| [24] |
PARIKH N, BOYD S. Proximal algorithms. Foundations and Trends® in Optimization, 2014, 1(3): 127-239. DOI:10.1561/2400000003 |
| [25] |
COTTER S F, RAO B D, ENGAN K, et al. Sparse solutions to linear inverse problems with multiple measurement vectors. IEEE Transactions on Signal Processing, 2005, 53(7): 2477-2488. DOI:10.1109/TSP.2005.849172 |
| [26] |
ELDAR Y C, RAUHUT H. Average case analysis of multichannel sparse recovery using convex relaxation. IEEE Transactions on Information Theory, 2010, 56(1): 505-519. DOI:10.1109/TIT.2009.2034789 |
| [27] |
JIN Y, RAO B D. Insights into the stable recovery of sparse solutions in overcomplete representations using network information theory. 2008 IEEE International Conference on Acoustics, Speech and Signal Processing, Las Vegas, 2008.
|
| [28] |
EDGAR J A, VAN DER BAAN M. How reliable is statistical wavelet estimation?. Geophysics, 2011, 76(4): V59-V68. DOI:10.1190/1.3587220 |
| [29] |
冯玮, 胡天跃, 姚逢昌, 等. 非稳态地震记录时变子波估计. 地球物理学报, 2017, 60(1): 305-315. FENG W, HU T Y, YAO F C, et al. Time-varying seismic wavelet estimation from nonstationary seismic data. Chinese Journal of Geophysics, 2017, 60(1): 305-315. |
| [30] |
夏洪瑞, 周开明, 黄桥, 等. 波阻抗反演技术中空变子波的求取. 石油物探, 2002, 41(4): 470-474. XIA H R, ZHOU K M, HUANG Q, et al. Calculation of spatialvariant wavelet in acoustic impedance inversion. Geophysical Prospecting for Petroleum, 2002, 41(4): 470-474. DOI:10.3969/j.issn.1000-1441.2002.04.019 |
| [31] |
刘晓晶, 印兴耀, 吴国忱, 等. 基于基追踪弹性阻抗反演的深部储层流体识别方法. 地球物理学报, 2016, 59(1): 277-286. LIU X J, YIN X Y, WU G C, et al. Identification of deep reservoir fluids based on basis pursuit inversion for elastic impedance. Chinese Journal of Geophysics, 2016, 59(1): 277-286. |
| [32] |
周东勇, 文晓涛, 贺振华, 等. MP算法在地震波阻抗反演中的应用. 成都理工大学学报(自然科学版), 2014, 41(1): 87-93. ZHOU D Y, WEN X T, HE Z H, et al. Application of matching pursuits to seismic inversion. Journal of Chengdu University of Technology(Science & Technology Edition), 2014, 41(1): 87-93. DOI:10.3969/j.issn.1671-9727.2014.01.11 |
| [33] |
YIN X Y, LIU X J, ZONG Z Y. Pre-stack basis pursuit seismic inversion for brittleness of shale. Petroleum Science, 2015, 12(4): 618-627. DOI:10.1007/s12182-015-0056-3 |
 2019, Vol. 31
2019, Vol. 31



