2. 石油工业出版社, 北京 100000;
3. 中国石油西南油气田分公司 勘探开发研究院, 成都 610000
2. Petroleum Industry Press, Beijing 100000, China;
3. Research Institute of Exploration and Development, PetroChina Southwest Oil and Gas Field Company, Chengdu 610000, China
我国非常规油气资源丰富、发展潜力大,高效开发非常规油气资源对于满足我国能源需求具有重要意义[1-2]。随着水力压裂技术的不断进步,为了改善油藏的开发效果,通常对水平井实施多段射孔压裂,增加油藏泄油面积,改善储层与井筒之间的流体连通状况,从而提高单井产量[3-4]。压力动态特征分析作为油气藏评价以及储层物性参数求取的重要手段,对于指导油气田开发具有重要意义。
点源函数的发展对于求解储层渗流模型解析解起到了重要作用。在早期,Gringarten等[5]基于Green函数得到实空间源函数解;Ozkan等[6-7]成功地将实空间源函数解扩展到Laplace空间;CincoLey等[8]建立并求解了倾斜水力压裂裂缝试井解释数学模型。水力压裂裂缝的分布因水力压裂过程中各种地质因素的存在而变得十分复杂[9]。关于水力压裂所形成的复杂裂缝试井模型,国内外均有研究,分别针对不对称缝[10-11]、多翼裂缝井[12]试井模型开展了研究,分析了其主控因素对压力和产量曲线的影响。多段压裂水平井对于高效开发储层原油具有重要的作用,研究其压力动态变化特征成为油气开发的重要环节,一些学者[13-21]对多段压裂水平井压力和产量模型进行了研究,考虑了裂缝倾斜和裂缝不对称的影响。水力压裂过程中井筒附近往往会形成压裂改造区,该区域储层渗透率高于储层原始渗透率。何吉祥等[22]和袁淋等[23]针对气、水两相压裂水平井产能计算给出了相关公式,并分析了水气体积比对产量曲线的影响。关于多段压裂水平井体积压裂改造试井模型的研究,姜瑞忠等[24]、苏玉亮等[25]、李道伦等[26]分别针对复合油藏多段压裂水平井试井模型展开研究,绘制了相应的典型特征曲线,并进行了影响因素分析。
在实际多段压裂体积改造时,由于地层条件复杂,导致井筒附近形成了复杂的缝网体积,因此,在前人研究成果的基础上,对水平井体积压裂改造试井模型进一步研究十分必要。针对水力压裂所形成的复杂裂缝,首先分别建立储层和裂缝试井解释数学模型,通过Laplace积分变换求得Laplace空间解析解,其次耦合储层与裂缝模型求解得到其均匀流量面源解,采用裂缝离散的方式求得Laplace空间井底压力解,最后通过Stehfest数值反演计算并绘制双对数曲线图,分析裂缝分布方式以及改造区半径对典型特征曲线的影响,以期为多段压裂水平井试井资料解释和压裂方式设计提供理论依据。
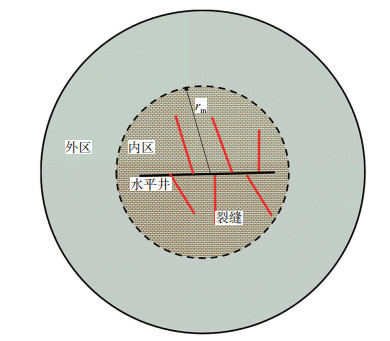
1 物理模型描述在水力压裂过程中由于地层条件等各种因素的影响,使得实际多段压裂水平井水力压裂裂缝分布不规律。水平井经多段压裂之后井筒附近储层的渗透率高于距井筒较远区域,即井筒附近由于压裂体积改造形成了压力改造区(内区),而未改造区(外区)储层渗透率不变。为了更好地建立水平井体积压裂改造试井数学模型,可以将多段压裂水平井裂缝分布物理模型抽象为径向复合模型,内区半径为rm(图 1)。其他假设条件如下:①内区和外区储层平均渗透率分别为k1,k2;②水平井位于顶底封闭、侧向无穷大外边界储层中;③裂缝宽度为wf且相等,第i条裂缝长度为Lfi,与井筒的夹角为θi,裂缝内渗透率为kf;④流体在储层和裂缝中的流动符合达西渗流规律,且为等温渗流;⑤每条裂缝都完全压开,即裂缝高度与储层厚度相等。
|
下载eps/tif图 图 1 多段压裂水平井裂缝分布物理模型示意图 Fig. 1 Schematic diagram of fracture distribution of multi-stage fractured well |
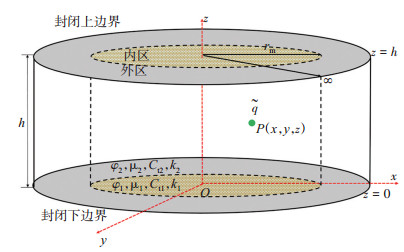
根据上述假设条件,顶底封闭、侧向无穷大外边界存在点源P,t = 0时刻从点源中采出流体的流量为
|
下载eps/tif图 图 2 径向复合油藏点源物理模型示意图 Fig. 2 Point-source schematic diagram with radial composite reservoirs |
对于多段压裂水平井复杂裂缝井底压力的计算,先以裂缝的单翼为研究对象建立储层试井解释数学模型,再根据压降叠加原理得到M条裂缝总的井底压降。根据状态方程、运动方程和连续性微分方程,分别得到无因次内区与外区渗流数学模型和边界条件,无因次变量定义为
关于无因次时间进行Laplace变化,得到Laplace空间方程组为
| $ \left\{ \begin{array}{l} \frac{1}{{{r_{\rm{D}}}}}\frac{\partial }{{\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{{\rm{D}}1}}}}{{\partial {r_{\rm{D}}}}}} \right) + \frac{{\partial {{\bar p}_{{\rm{D}}1}}}}{{\partial z_{\rm{D}}^2}} = s{{\bar p}_{{\rm{D}}1}}\quad \left( {1 \le {r_{\rm{D}}} \le {r_{{\rm{mD}}}}} \right)\\ \frac{1}{{{r_{\rm{D}}}}}\frac{\partial }{{\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{{\rm{D2}}}}}}{{\partial {r_{\rm{D}}}}}} \right) + \frac{{\partial {{\bar p}_{{\rm{D2}}}}}}{{\partial z_{\rm{D}}^2}} = {\eta _{12}}s{{\bar p}_{{\rm{D2}}}}\quad \left( {{r_{{\rm{mD}}}} \le {r_{\rm{D}}} \le \infty } \right)\\ \mathop {\lim }\limits_{{\varepsilon _{\rm{D}}} \to 0} {\left( {{r_{\rm{D}}}\frac{{\partial {p_{{\rm{D}}1}}}}{{\partial {r_{\rm{D}}}}}} \right)_{{r_{\rm{D}}} = {\varepsilon _{\rm{D}}}}} = - {\overline {\tilde q} _{\rm{D}}}\\ {M_{12}}{\left( {\frac{{\partial {{\bar p}_{{\rm{D}}1}}}}{{\partial {r_{\rm{D}}}}}} \right)_{{r_{\rm{D}}} = {r_{{\rm{mD}}}}}} = {\left( {\frac{{\partial {{\bar p}_{{\rm{D}}2}}}}{{\partial {r_{\rm{D}}}}}} \right)_{{{\rm{r}}_{\rm{D}}} = {r_{{\rm{mD}}}}}}\\ {{\bar p}_{{\rm{D}}1}}\left( {{r_{{\rm{mD}}}}, s} \right) = {{\bar p}_{{\rm{D}}2}}\left( {{r_{{\rm{mD}}}}, s} \right)\\ {{\bar p}_{{\rm{D}}2}}\left( {{r_{\rm{D}}} \to \infty , s} \right) = 0 \end{array} \right. $ | (1) |
分别对内区和外区渗流微分方程关于zD从0到hD进行有限余弦Fourier变换,得到只考虑径向方向的径向复合渗流微分方程,根据Bessel方程基本解的结构,得到内外区渗流微分方程的通解,再根据有限余弦Fourier逆变换得到内外区任意位置处点源解为
| $ {{\bar p}_{{\rm{D1}}}} = \left\{ {{a_1}{I_0}\left( {{\varepsilon _0}{r_{\rm{D}}}} \right) + {a_2}{K_0}\left( {{\varepsilon _0}{r_{\rm{D}}}} \right) + 2\sum\limits_{n = 1}^\infty {\left[ {{a_{1n}}{I_0}\left( {{\varepsilon _n}{r_{\rm{D}}}} \right) + {a_{2n}}{K_0}\left( {{\varepsilon _n}{r_{\rm{D}}}} \right)} \right]} \cos \left( {\frac{{n{\rm{ \mathit{ π} }}{z_{\rm{D}}}}}{{{h_{\rm{D}}}}}} \right)\cos \left( {\frac{{n{\rm{ \mathit{ π} }}{z_{{\rm{wD}}}}}}{{{h_{\rm{D}}}}}} \right)} \right\} $ | (2) |
| $ {{\bar p}_{{\rm{D}}2}} = \left\{ {{b_1}{I_0}\left( {{\varepsilon _0}{r_{\rm{D}}}} \right) + {b_2}{K_0}\left( {{\varepsilon _0}{r_{\rm{D}}}} \right) + 2\sum\limits_{n = 1}^\infty {\left[ {{b_{1n}}{I_0}\left( {{\varepsilon _n}{r_{\rm{D}}}} \right) + {b_{2n}}{K_0}\left( {{\varepsilon _n}{r_{\rm{D}}}} \right)} \right]} \cos \left( {\frac{{n{\rm{ \mathit{ π} }}{z_{\rm{D}}}}}{{{h_{\rm{D}}}}}} \right)\cos \left( {\frac{{n{\rm{ \mathit{ π} }}{z_{{\rm{wD}}}}}}{{{h_{\rm{D}}}}}} \right)} \right\} $ | (3) |
其中
| $ \begin{array}{*{20}{c}} {{\varepsilon _n} = \sqrt {s + \frac{{{n^2}{{\rm{ \mathit{ π} }}^2}}}{{{h_{\rm{D}}}}}} }\\ {{\varepsilon _{n1}} = \sqrt {{\eta _{12}}s + \frac{{{n^2}{{\rm{ \mathit{ π} }}^2}}}{{{h_{\rm{D}}}}}} \;\;\;\;\;(n = 0, 1, 2, 3, \cdots )} \end{array} $ |
| $ {r_{\rm{D}}} = \sqrt {{{\left( {{x_{\rm{D}}} - {x_{{\rm{wD}}}}} \right)}^2} + {{\left( {{y_{\rm{D}}} - {y_{{\rm{wD}}}}} \right)}^2}} $ |
式中:s为拉普拉斯变量;I0(x)为零阶第1类修正Bessel函数;K0(x)为零阶第2类修正Bessel函数。
联立内外边界条件并根据内外区界面条件得到式(2)和式(3)中的系数分别为
| $ {{a}_{1n}}=\frac{{{K}_{0}}\left( {{\varepsilon }_{n}}{{r}_{\text{mD}}} \right)K_{0}^{\prime }\left( {{\varepsilon }_{n1}}{{r}_{\text{mD}}} \right)-{{M}_{12}}K_{0}^{\prime }\left( {{\varepsilon }_{n}}{{r}_{\text{mD}}} \right){{K}_{0}}\left( {{\varepsilon }_{n1}}{{r}_{\text{mD}}} \right)}{{{M}_{12}}I_{0}^{\prime }\left( {{\varepsilon }_{n}}{{r}_{\text{mD}}} \right){{K}_{0}}\left( {{\varepsilon }_{n1}}{{r}_{\text{mD}}} \right)-{{I}_{0}}\left( {{\varepsilon }_{n}}{{r}_{\text{mD}}} \right)K_{0}^{\prime }\left( {{\varepsilon }_{n1}}{{r}_{\text{mD}}} \right)}{{{\bar{\tilde{q}}}}_{\text{D}}} $ |
| $ {{a}_{2n}}={{{\bar{\tilde{q}}}}_{\text{D}}} $ |
| $ {{b_{1n}} = 0} $ |
| $ {{b}_{2n}}=\frac{{{\eta }_{12}}{{M}_{12}}}{{{r}_{\text{mD}}}}\frac{{{{\bar{\tilde{q}}}}_{\text{D}}}}{{{M}_{12}}I_{0}^{\prime }\left( {{\varepsilon }_{n}}{{r}_{\text{mD}}} \right){{K}_{0}}\left( {{\varepsilon }_{n1}}{{r}_{\text{mD}}} \right)-{{I}_{0}}\left( {{\varepsilon }_{n}}{{r}_{\text{mb}}} \right)K_{0}^{\prime }\left( {{\varepsilon }_{n1}}{{r}_{\text{mb}}} \right)} $ |
根据Ozkan等[6-7]和Restrepo等[27]的研究,为了求得任意形状裂缝的井底压力解,对式(2)分别关于zD从0到hD和关于xD从0到LfD积分得到均匀流量面源解,再根据坐标变换和坐标旋转得到第i条裂缝均匀流量面源解为
| $ \begin{align} & {{{\bar{p}}}_{\text{Dl}i}}\left( {{r}_{\text{D}}},{{\theta }_{i}},{{y}_{\text{wD}}},u \right)=\int_{0}^{{{L}_{\text{fD}i}}}{{{{\bar{\tilde{q}}}}_{\text{D}i}}}\left( \alpha ,{{\theta }_{i}},u \right)\times \left[ {{K}_{0}}\left( {{\varepsilon }_{0}}{{R}_{\text{D}}} \right)+ \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left. {{a}_{1}}{{I}_{0}}\left( {{\varepsilon }_{0}}{{R}_{\text{D}}} \right) \right]\text{d}\alpha \\ \end{align} $ | (4) |
其中
| $ {R_{\rm{D}}} = \sqrt {{{\left( {{r_{\rm{D}}}\cos \theta - \alpha \cos {\theta _i}} \right)}^2} + {{\left( {{r_{\rm{D}}}\sin \theta - {y_{{\rm{wD}}}} - \alpha \sin {\theta _i}} \right)}^2}} $ |
M条裂缝总的压降可以写为
| $ {{\bar p}_{{\rm{D}}1}} = \sum\limits_{i = 1}^M {{{\bar p}_{{\rm{Dl}}i}}} \left( {{r_{\rm{D}}}, {\theta _i}, {y_{{\rm{wD}}}}, u} \right) $ | (5) |
根据质量守恒关系,M条裂缝的总流量等于每条裂缝流量的总和。
| $ \sum\limits_{i=1}^{M}{\int_{0}^{{{L}_{\text{fDi}}}}{{{{\bar{\tilde{q}}}}_{\text{D}i}}}}\left( \alpha ,{{\theta }_{i}},u \right)\text{d}\alpha =\frac{1}{s} $ | (6) |
基于Cinco-Ley等[8]的研究,建立裂缝数学模型,经坐标旋转之后使裂缝沿坐标方向分布,假定所有裂缝的宽度都相等,基于渗流力学基本原理,第i条裂缝Laplace空间无因次裂缝数学模型为
| $ \left\{ \begin{array}{*{35}{l}} \frac{\partial }{\partial {{r}_{\text{D}i}}}\left( \frac{\partial {{{\bar{p}}}_{\text{fD}i}}}{\partial {{r}_{\text{D}i}}} \right)-\frac{2\text{ }\!\!\pi\!\!\text{ }}{{{C}_{\text{fD}}}}{{{\bar{\tilde{q}}}}_{\text{fD}}}=0 \\ {{\left. \frac{\partial {{{\bar{p}}}_{\text{fD}i}}}{\partial {{r}_{\text{D}i}}} \right|}_{{{r}_{\text{D}i}}=0}}=-\frac{2\text{ }\!\!\pi\!\!\text{ }}{{{C}_{\text{fD}i}}}{{{\bar{q}}}_{\text{fD}i}} \\ \left( {{\frac{\partial {{{\bar{p}}}_{\text{fD}i}}}{\partial {{r}_{\text{D}i}}}}_{{{r}_{\text{D}i}}={{L}_{\text{fD}i}}}}=0 \right) \end{array} \right. $ | (7) |
对式(7)进行2次Green函数积分得到
| $ \begin{align} & {{{\bar{p}}}_{\text{fD}i}}\left( {{r}_{\text{D}i}},{{\theta }_{i}},s \right)-{{{\bar{p}}}_{\text{wHD}i}}=\frac{2\text{ }\!\!\pi\!\!\text{ }}{{{C}_{\text{fD}i}}}\left( \int_{0}^{{{r}_{\text{D}}}}{\int_{0}^{\alpha }{{{{\bar{\tilde{q}}}}_{\text{fD}}}}}\text{d}\alpha \text{d}{{r}_{\text{D}}}- \right. \\ & \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left. {{r}_{\text{D}i}}\int_{0}^{{{L}_{\text{fD}i}}}{{{{\bar{\tilde{q}}}}_{\text{fD}}}}\text{d}\alpha \right) \\ \end{align} $ | (8) |
在裂缝壁面处压力和流量相等,根据裂缝模型与储层模型在裂缝壁面处的衔接条件得到井底压力解。因此,有如下表达式:
| $ {\left. {{{\bar p}_{{\rm{fD}}i}}\left( {{r_{{\rm{D}}i}}, {\theta _i}, s} \right)} \right|_{{r_{{\rm{D}}i}}\tan {\theta _i} = \pm \frac{{{W_{\rm{f}}}}}{2}}} = {\left. {{{\bar p}_{{\rm{D}}1i}}\left( {{r_{{\rm{D}}i}}, {\theta _i}, s} \right)} \right|_{{r_{{\rm{D}}i}}{\rm{tan}}{\theta _i} = \pm \frac{{{W_{\rm{f}}}}}{2}}} $ | (9) |
| $ {{\left. {{{\bar{\tilde{q}}}}_{\text{fD}}}\left( {{r}_{\text{D}i}},{{\theta }_{i}},s \right) \right|}_{{{r}_{\text{D}i}}\tan {{\theta }_{i}}=\pm \frac{{{W}_{\text{f}}}}{2}}}={{\left. {{{\bar{\tilde{q}}}}_{\text{D}}}\left( {{r}_{\text{D}i}},{{\theta }_{i}},s \right) \right|}_{{{r}_{\text{D}i}}\tan {{\theta }_{i}}=\pm \frac{{{W}_{\text{f}}}}{2}}} $ | (10) |
将式(4)、式(9)和式(10)代入式(8)得到
| $ \begin{align} & {{{\bar{p}}}_{\text{wHD }}}-\sum\limits_{i=1}^{M}{\int_{0}^{{{L}_{\text{fD}i}}}{{{{\bar{\tilde{q}}}}_{\text{D}i}}}}\left( \alpha ,{{\theta }_{i}},u \right)\times \left[ {{K}_{0}}\left( {{\varepsilon }_{0}}{{R}_{\text{D}}} \right)+{{a}_{1}}{{I}_{0}}\left( {{\varepsilon }_{0}}{{R}_{\text{D}}} \right) \right]\text{d}\alpha \\ & \ \ \ =\frac{2\text{ }\!\!\pi\!\!\text{ }}{{{C}_{\text{fD}i}}}\left( {{r}_{\text{D}i}}\int_{0}^{{{L}_{\text{fD}i}}}{{{{\bar{\tilde{q}}}}_{\text{D}}}}\text{d}\alpha -\int_{0}^{{{r}_{\text{D}}}}{\int_{0}^{\alpha }{{{{\bar{\tilde{q}}}}_{\text{D}}}}}\text{d}\alpha \text{d}{{r}_{\text{D}}} \right) \\ \end{align} $ | (11) |
式(11)中含有Fredholm积分方程,直接求解比较困难,基于均匀流量模型解,将每条裂缝离散为N段,每段流量均不变,式(6)和式(11)离散之后的表达式为
| $ \begin{array}{*{20}{c}} {{{\bar p}_{{\rm{wHD }}}} - \sum\limits_{i = 1}^M {\sum\limits_{j = 1}^N {\int\limits_{{r_{{{\rm{D}}_{i, j}}}}}^{{r_{{{\rm{D}}_{i, j + 1}}}}} {{{\bar q}_{{\rm{D}}i, j}}} } } \left\{ {{K_0}[\sqrt s \sqrt {{{\left( {{r_{{\rm{wD}}m, k}}\cos {\theta _m} - \alpha \cos {\theta _i}} \right)}^2} + {{\left( {{r_{{\rm{wD}}m, k}}\sin {\theta _m} - {y_{{\rm{wD}}i}} - \alpha \sin {\theta _i}} \right)}^2}} ] + } \right.}\\ {\left. {{a_1}{I_0}[\sqrt s \sqrt {{{\left( {{r_{{\rm{wD}}m, k}}\cos {\theta _m} - \alpha \cos {\theta _i}} \right)}^2} + {{\left( {{r_{{\rm{wD}}m, k}}\sin {\theta _m} - {y_{{\rm{wD}}i}} - \alpha \sin {\theta _i}} \right)}^2}} ]} \right\}{\rm{d}}\alpha = \frac{{2{\rm{ \mathit{ π} }}}}{{{C_{{\rm{fD}}i}}}} \cdot }\\ {\left\{ {{r_{{\rm{wD}}m, k}}\sum\limits_{k = 1}^{{N_m}} {{{\bar q}_{{\rm{fD}}m, k}}} \Delta {r_{{\rm{D}}m}} - \frac{{\Delta r_{{\rm{D}}m{\rm{ }}}^2}}{8}{{\bar q}_{{\rm{fD}}m, k}} - \sum\limits_{j = 1}^{k - 1} {{{\bar q}_{{\rm{fD}}m, k}}} \left[ {(k - j)\Delta r_{{\rm{D}}m{\rm{ }}}^2} \right]} \right\}\left( {1 \le m \le M, 1 \le k \le N} \right)} \end{array} $ | (12) |
| $ \sum\limits_{i=1}^{M}{\sum\limits_{j=1}^{N}{{{{\bar{\tilde{q}}}}_{\text{fD}i}}}}\Delta {{r}_{\text{D}i}}=\frac{1}{s} $ | (13) |
其中
| $ \begin{array}{*{20}{c}} {\Delta {r_{{\rm{D}}i}} = \frac{{{L_{{\rm{fD}}i}}}}{N}}\\ {{r_{{\rm{wD}}i, j}} = j\Delta {r_{{\rm{D}}i, j}} - \frac{{\Delta {r_{{\rm{D}}i}}}}{2}}\\ {{r_{{\rm{D}}i, j}} = (j - 1)\Delta {r_{{\rm{D}}i}}} \end{array} $ |
式中:Δ rDi为第i条裂缝第j个网格步长;rwDi, j为第i条裂缝第j个网格中点;rDi, j为第i条裂缝第j个网格端点;M为裂缝条数;N为裂缝离散个数。
利用上述M×N + 1个方程组求得M×N + 1个未知数,从而求得井底压力解。
当裂缝条数M = 2时,裂缝不对称因子定义为
| $ \beta = \frac{{\left| {{L_{{\rm{fl}}}} - {L_{{\rm{f2}}}}} \right|}}{{{L_{{\rm{fl}}}} + {L_{{\rm{f2}}}}}} $ | (14) |
根据Duhamel原理,考虑井储和表皮效应影响时无因次井底压力表示为
| $ {{\bar p}_{{\rm{wD}}}} = \frac{{s{{\bar p}_{{\rm{wHD}}}} + S}}{{s + {C_{\rm{D}}}{s^2}\left( {s{{\bar p}_{{\rm{wHD}}}} + S} \right)}} $ | (15) |
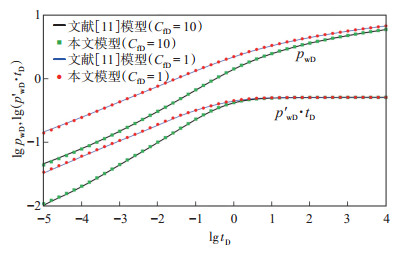
在进行模型验证时,如果本文模型M = 2,Lf1 = 20,Lf2 = 60,θ1 = 0°,θ2 = 180°,该模型就可以简化为不对称垂直裂缝,并与文献[11]针对不对称垂直裂缝的计算结果进行对比。对于有限导流裂缝而言,裂缝导流能力的大小对于计算的准确性和精度都有很大的影响,因此,分别取无因次裂缝导流能力为1和10进行对比,从图 3可以看出无论无因次裂缝导流能力是大还是小,文献[11]的计算结果都能与本文简化模型计算结果吻合。需要注意的是,当裂缝导流能力很低时,将单个裂缝离散的段数越多,计算结果越准确。
|
下载eps/tif图 图 3 模型验证对比 Fig. 3 Comparison of model verification |
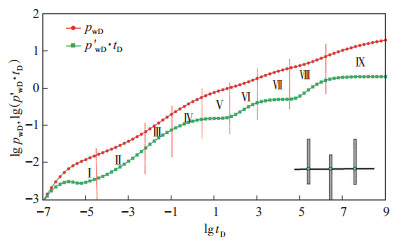
图 4为复合油藏多段压裂水平井复杂裂缝分布井底压力响应特征曲线。根据压力导数曲线特征,该典型特征曲线可以分为9个流动阶段:第Ⅰ阶段为井储阶段,纯井储阶段该曲线特征表现为压力和压力导数曲线重合,且斜率均为1;第Ⅱ阶段为双线性流阶段,该阶段储层内流体向裂缝流动和裂缝内流体向井筒流动同时发生,理想状态下该阶段压力导数曲线呈斜率为1/4的直线;第Ⅲ阶段为线性流阶段,该阶段只有储层内流体向裂缝流动,理想状态下该阶段压力导数曲线呈斜率为1/2的直线;第Ⅳ阶段为早期椭圆流阶段,该阶段为流体围绕单个裂缝的椭圆流;第Ⅴ阶段为早期径向流阶段,该阶段为流体围绕单个裂缝的径向流,压力导数曲线为0.5/M的水平线;第Ⅵ阶段为过渡流阶段;第Ⅶ阶段为内区径向流阶段,该阶段为内区流体围绕水平井的径向流,压力导数曲线为0.5的水平线;第Ⅷ阶段为内区向外区过渡流阶段;第Ⅸ阶段为外区径向流阶段,该阶段为整个储层流体围绕水平井的径向流,表现为外区径向流特征,压力导数曲线为0.5 M12的水平线。
|
下载eps/tif图 图 4 复合油藏多段压裂水平井复杂裂缝分布井底压力响应特征曲线 右下角为多段压裂水平井裂缝分布示意图 Fig. 4 Wellbore pressure response curve of multi-stage fractured horizontal well with complex fracture in composite reservoirs |
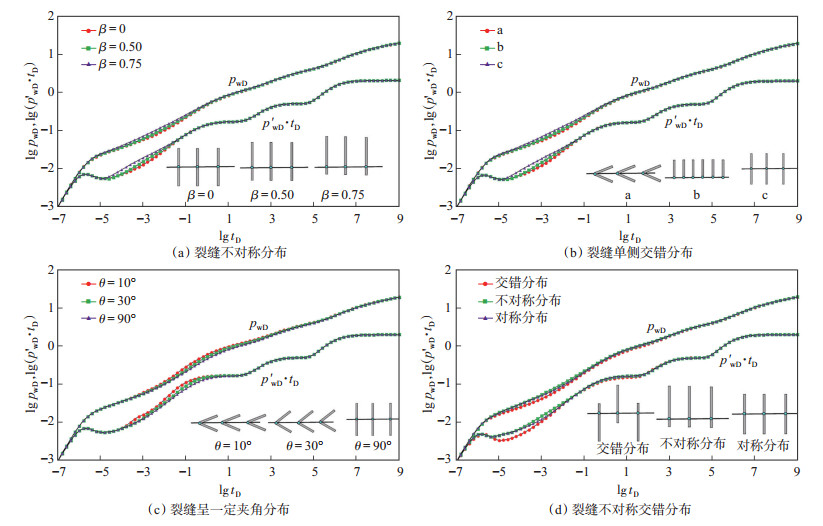
图 5为裂缝分布方式对压力响应特征曲线的影响。地层应力分布不均匀和射孔压裂都会导致压裂裂缝呈现出不对称分布、单侧交错分布、不对称交错分布及呈一定夹角分布。单裂缝呈现出不对称分布时,裂缝不对称只影响早期线性流和双线性流阶段压力和压力导数曲线的变化,裂缝越不对称,早期阶段流体流入井筒所消耗的压力越大,压力和压力导数曲线均越高[图 5(a)]。在水平井长度和裂缝条数相等的条件下,当沿水平井一侧压开或以一定的夹角两侧压开时,裂缝与井筒夹角越小,流体流入裂缝所消耗的压降越大。当裂缝单侧压开时,由于b情形缝间距离是c情形的一半,因此,早期径向流阶段压力导数曲线低[图 5(b)]。当裂缝呈a,b,c等3种情形分布时,c情形下流体流入井筒所消耗的压力最低。当裂缝与井筒存在一定夹角时,裂缝与水平井筒所存在的夹角越小,裂缝所控制的流体范围越小,裂缝与裂缝之间的干扰性越强,因此,裂缝与井筒之间的夹角越小,双对数坐标压力和压力导数曲线均越高[图 5(c)]。裂缝交错分布可以有效地扩大裂缝控制区域,当裂缝呈现不对称式交错分布时,裂缝与裂缝之间长短互补可以有效地使井筒附近流体流入井筒时所消耗的压力变小,因此,相比于对称分布和不对称分布,当裂缝呈不对称交错分布时早期压力和压力导数曲线均最低[图 5(d)]。
|
下载eps/tif图 图 5 裂缝分布方式对压力响应特征曲线的影响 右下角为多段压裂水平井裂缝分布示意图 Fig. 5 Effects of fracture distribution on wellbore pressure response curves |
结合以上几种裂缝分布方式来看,当裂缝呈不对称交错分布时可以更有效地降低流体流入井筒所消耗的压力,从而可以最大限度地提高单井产量。因此,在实际压裂过程中应避免裂缝不对称分布、单侧分布及呈夹角分布的情形。
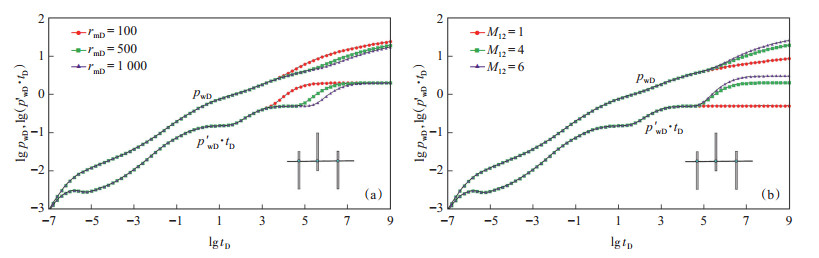
3.4 内区半径大小和流度比对曲线的影响图 6反映了内区半径大小和流度比对压力响应特征曲线的影响。水平井体积压裂之后所形成的内区大小和内区渗透率大小都对压力响应特征曲线有很大的影响。内区半径主要影响内区径向流持续时间长短和曲线形态,较大的内区半径容易形成内区径向流,因此,在压力导数曲线上其0.5水平线也越长;此外,内区半径越大,储层改造范围越大,流体流入井筒所消耗的压力损失越小,对应的压力曲线越靠下[图 6(a)]。内外区流度比是指径向复合油藏内区与外区流动系数比值的大小,内外区流度比越大,外区径向流阶段压力导数值为0.5 M12的水平线越高。由于内区渗透率增大,流体流动阻力减小,因此,内外区流度比越大,对应的压力曲线越高[图 6(b)]。
|
下载eps/tif图 图 6 内区半径(a)和内外区流度比(b)对压力响应特征曲线的影响 右下角为多段压裂水平井裂缝分布示意图 Fig. 6 Effects of inner radius(a)and mobility ratio(b)on wellbore pressure response curves |
(1)综合考虑裂缝不对称、裂缝夹角等因素,建立了径向复合油藏多段压裂水平井复杂裂缝分布试井数学模型,通过Laplace变换和Stehfest数值反演得到了定产条件下的井底压力解。通过对比、分析,验证了本文模型的正确性。
(2)根据压力导数曲线特征,本文模型压力动态特征曲线主要的流动阶段有6个,即井储阶段(斜率为1)、双线性流阶段(斜率为1/4)、线性流阶段(斜率为1/2)、早期径向流阶段(0.5/M水平线)、内区径向流阶段(0.5水平线)和外区径向流阶段(0.5 M12水平线)。
(3)综合分析各种裂缝分布方式,当裂缝不对称交错分布时压裂改造效果最好,压力曲线越低;内区半径越大,内外区流度比越小,外区径向流阶段压力曲线越靠下。
| [1] |
邱振, 邹才能, 李建忠, 等. 非常规油气资源评价进展与未来展望. 天然气地球科学, 2013, 24(2): 238-246. QIU Z, ZOU C N, LI J Z, et al. Unconventional petroleum resources assessment:Progress and future prospects. Natural Gas Geoscience, 2013, 24(2): 238-246. |
| [2] |
贾承造, 郑民, 张永峰. 中国非常规油气资源与勘探开发前景. 石油勘探与开发, 2012, 39(2): 129-136. JIA C Z, ZHENG M, ZHANG Y F. Unconventional hydrocarbon resources in China and the prospect of exploration and development. Petroleum Exploration and Development, 2012, 39(2): 129-136. |
| [3] |
曾凡辉, 郭建春, 徐严波, 等. 压裂水平井产能影响因素. 石油勘探与开发, 2007, 34(4): 474-477. ZENG F H, GUO J C, XU Y B, et al. Factors affecting production capacity of fractured horizontal wells. Petroleum Exploration and Development, 2007, 34(4): 474-477. DOI:10.3321/j.issn:1000-0747.2007.04.016 |
| [4] |
徐严波, 齐桃, 杨凤波, 等. 压裂后水平井产能预测新模型. 石油学报, 2006, 27(1): 89-91. XU Y B, QI T, YANG F B, et al. New model for productivity test of horizontal well after hydraulic fracturing. Acta Petrolei Sinica, 2006, 27(1): 89-91. DOI:10.3321/j.issn:0253-2697.2006.01.019 |
| [5] |
GRINGARTEN A C, RAMEY JR H J. The use of source and Green's functions in solving unsteady-flow problems in reservoirs. SPE Journal, 1973, 13(5): 285-296. |
| [6] |
OZKAN E, RAGHAVAN R. New solutions for well-test analysis problems:Part 1-Analytical considerations. SPE Formation Evaluation, 1991, 6(3): 359-368. DOI:10.2118/18615-PA |
| [7] |
OZKAN E, RAGHAVAN R. New solutions for well-test-analysis problems:part 2-Computational considerations and applications. SPE Formation Evaluation, 1991, 6(3): 369-378. DOI:10.2118/18616-PA |
| [8] |
CINCO-LEY H, MILLER F G, RAMEY H J. Unsteady-state pressure distribution created by a directionally drilled well. Journal of Petroleum Technology, 1975, 27(11): 1392-1400. DOI:10.2118/5131-PA |
| [9] |
崔明月, 刘玉章, 修乃领, 等. 形成复杂缝网体积(ESRV)的影响因素分析. 石油钻采工艺, 2014, 36(2): 82-87. CUI M Y, LIU Y Z, XIU N L, et al. Analysis of factors affecting the formation of effective stimulated reservoir volume(ESRV). Oil Drilling & Production Technology, 2014, 36(2): 82-87. |
| [10] |
BERUMEN S, TIAB D, RODIGUEZ F. Constant rate solutions for a fractured well with an asymmetric fracture. Journal of Petroleum Science & Engineering, 2000, 25(1): 49-58. |
| [11] |
WANG L, WANG X P. Type curves analysis for asymmetrically fractured wells. Journal of Energy Resources Technology, 2014, 136(2): 119-129. |
| [12] |
TIAN Q, LIU P C, JIAO Y W, et al. Pressure transient analysis of non-planar asymmetric fractures connected to vertical wellbores in hydrocarbon reservoirs. International Journal of Hydrogen Energy, 2017, 42: 18146-18155. DOI:10.1016/j.ijhydene.2017.04.161 |
| [13] |
曹宝军, 李相方, 姜子杰, 等. 压裂火山岩气井不对称裂缝产能模型研究. 天然气工业, 2009, 29(8): 79-81. CAO B J, LI X F, JIANG Z J, et al. A research on the asymmetric fracture productivity models for fracturing volcanic gas wells. Natural Gas Industry, 2009, 29(8): 79-81. DOI:10.3787/j.issn.1000-0976.2009.08.025 |
| [14] |
王本成, 贾永禄, 李友全, 等. 多段压裂水平井试井模型求解新方法. 石油学报, 2013, 34(6): 1150-1156. WANG B C, JIA Y L, LI Y Q, et al. A new solution of well test model for multistage fractured horizontal wells. Acta Petrolei Sinica, 2013, 34(6): 1150-1156. |
| [15] |
樊冬艳, 姚军, 孙海, 等. 页岩气藏分段压裂水平井不稳定渗流模型. 中国石油大学学报(自然科学版), 2014, 38(5): 116-123. FAN D Y, YAO J, SUN H, et al. Transient flow model of stagefractured horizontal wells in shale gas reservoirs. Journal of China University of Petroleum(Science & Technology Edition), 2014, 38(5): 116-123. DOI:10.3969/j.issn.1673-5005.2014.05.016 |
| [16] |
方思冬, 战剑飞, 黄世军, 等. 致密油藏多角度裂缝压裂水平井产能计算方法. 油气地质与采收率, 2015, 22(3): 84-89. FANG S D, ZHAN J F, HUANG S J, et al. A computational method for productivity of arbitrary angular fractured horizontal well in tight oil reservoirs. Petroleum Geology and Recovery Efficiency, 2015, 22(3): 84-89. DOI:10.3969/j.issn.1009-9603.2015.03.015 |
| [17] |
王家航, 王晓冬, 董文秀, 等. 非均质油藏多段压裂水平井不稳态压力分析半解析方法. 东北石油大学学报, 2017, 41(5): 90-99. WANG J H, WANG X D, DONG W X, et al. Semi-analytical approach to model pressure transients of multiple-fractured horizontal wells in heterogeneous reservoirs. Journal of Northeast Petroleum University, 2017, 41(5): 90-99. DOI:10.3969/j.issn.2095-4107.2017.05.010 |
| [18] |
王镜惠, 梅明华, 梁正中, 等. 水平井多段压裂非常规裂缝压力动态特征. 新疆石油地质, 2018, 39(1): 97-103. WANG J H, MEI M H, LIANG Z Z, et al. Dynamic pressure characteristics of unconventional fractures during multi-staged fracturing in horizontal well. Xinjiang Petroleum Geology, 2018, 39(1): 97-103. |
| [19] |
任宗孝, 吴晓东, 屈展, 等. 倾斜裂缝水平井非稳态压力模型. 石油学报, 2017, 38(9): 1059-1065. REN Z X, WU X D, QU Z, et al. Transient pressure model for horizontal wells with inclined fractures. Acta Petrolei Sinica, 2017, 38(9): 1059-1065. |
| [20] |
苏皓, 雷征东, 张荻萩, 等. 致密油藏体积压裂水平井参数优化研究. 岩性油气藏, 2018, 30(4): 140-148. SU H, LEI Z D, ZHANG D Q, et al. Volume fracturing parameters optimization of horizontal well in tight reservoir. Lithologic Reservoirs, 2018, 30(4): 140-148. |
| [21] |
王新杰. 致密气藏压裂水平井产能计算方法. 岩性油气藏, 2018, 30(5): 161-168. WANG X J. Calculation method for productivity of fractured horizontal well in tight gas reservoir. Lithologic Reservoirs, 2018, 30(5): 161-168. |
| [22] |
何吉祥, 姜瑞忠, 毛瑜, 等. 致密气藏气水两相压裂水平井产能计算方法. 岩性油气藏, 2017, 29(4): 154-161. HE J X, JIANG R Z, MAO Y, et al. Productivity calculation method for gas-water two phase fractured horizontal wells in tight gas reservoir. Lithologic Reservoirs, 2017, 29(4): 154-161. DOI:10.3969/j.issn.1673-8926.2017.04.019 |
| [23] |
袁淋, 李晓平, 刘建军. 低渗透气藏气水同产压裂水平井产能计算方法. 岩性油气藏, 2016, 28(4): 88-94. YUAN L, LI X P, LIU J J. Productivity calculation method of fractured horizontal wells with gas-water two-phase in low permeability gas reservoirs. Lithologic Reservoirs, 2016, 28(4): 88-94. DOI:10.3969/j.issn.1673-8926.2016.04.012 |
| [24] |
姜瑞忠, 滕文超, 乔欣, 等. 复合页岩气藏压裂水平井压力动态分析. 天然气地球科学, 2015, 26(12): 2336-2342. JIANG R Z, TENG W C, QIAO X, et al. Pressure transient analysis of fractured horizontal well in composite shale gas reservoir. Natural Gas Geoscience, 2015, 26(12): 2336-2342. DOI:10.11764/j.issn.1672-1926.2015.12.2336 |
| [25] |
苏玉亮, 王文东, 盛广龙. 体积压裂水平井复合流动模型. 石油学报, 2014, 35(3): 504-510. SU Y L, WANG W D, SHENG G L. Compound flow model of volume fractured horizontal well. Acta Petrolei Sinica, 2014, 35(3): 504-510. |
| [26] |
李道伦, 杨景海, 闫术, 等. 致密油大规模多段压裂水平试井解释及外区渗透率对试井曲线的影响. 地球科学, 2017, 42(8): 1324-1332. LI D L, YANG J H, YAN S, et al. Numerical well test interpretation of massive multistage fractured horizontal well in tight oil reservoirs and effect of permeability of exterior region on well test curves. Earth Science, 2017, 42(8): 1324-1332. |
| [27] |
RESTREPO D, TIAB D. Multiple fractures transient response. SPE 121594, 2009.
|
 2019, Vol. 31
2019, Vol. 31




