2. 中海油研究总院有限责任公司, 北京 100028;
3. 西安石油大学 地球科学与工程学院, 西安 710000
2. CNOOC Research Institute Co., Ltd., Beijing 100028, China;
3. College of Earth Sciences and Engineering, Xi'an Shiyou University, Xi'an 710000, China
缝洞型油藏的孔洞、基质及裂缝系统相互影响,为了描述其储层复杂的孔隙结构,出现了三重介质模型的概念[1-2]。描述缝洞型碳酸盐岩油藏的渗流特征,须充分考虑裂缝系统的分形特征、致密基质块的非线性渗流特征,以及储层的应力敏感性[3-5]。
国内外学者针对三重介质模型进行了深入的研究。姚军等[6]创新变井筒储存三重介质油藏试井理论,对介质间窜流、弹性储容比及变井储参数对压力响应的影响进行了研究。Camacho-Velazquez等[7]对所建立的三重孔隙模型考虑了溶洞系统与井筒连通和不连通2种情况下的解,并对样板曲线进行了详细的研究。李成勇等[8]建立了三重介质油藏的水平井各向异性渗流数学模型,并对水平井的压力动态进行了系统的研究。张冬丽等[9]建立了三重介质数值试井模型,很好地反映出了缝洞型储层的非均质性特征,该数值试井模型可进一步考虑缝洞型油藏中具体的裂缝和溶洞,进而推广至两相流试井。Gomez等[10]利用全局最优化解法对缝洞型储层试井曲线解释方法进行研究,提高了计算效率和试井解释精度。Li等[11]对不同边界条件下缝洞型储层的动态特征进行了研究,形成了一套系统的刻画缝洞型储层动态特征的方法。不仅如此,分形理论在储层渗流领域的应用也取得了较大的进展。Chang等[12]提出了分形裂缝网络嵌入基质的表征公式,并通过对扩散方程系数的适当修正来描述分形系统中的单相流动。Acuna等[13]将分形理论应用于裂缝性储层试井中,并基于试井解释明确了分形参数的物理意义。Razminia等[14]利用分形几何和分数阶微积分的概念分析了两区复合储层的数学模型,并推导了径向复合系统中井底瞬态压力解。张本健等[15]针对裂缝性气藏试井渗流问题,使用分形网络模拟气藏裂缝系统并将分形网络嵌入到气藏中,计算出试井模型的流动动态特征典型曲线,结果表明分形网络能够很好地模拟裂缝性气藏的渗流特征。
虽然目前对三重介质模型的研究较多,但仍存在无法精确表征储层非均质性特征的问题,而分形理论的应用使得非均质储层,尤其是裂缝的表征更灵活且更贴近实际,但该理论在缝洞型储层中的应用研究较少且未成体系。此外,对缝洞型储层致密基质块非线性渗流特征的研究也不可忽视。研究低渗储层最常用的渗流模型主要有拟启动压力梯度模型、分段模型及连续模型,这3种模型均由不同数学函数拟合实验数据所得,缺乏物理背景,表征不够灵活。
针对缝洞型碳酸盐岩储层渗流模型目前存在的问题,综合考虑裂缝分形特征和基质系统非线性渗流机理,完善非线性渗流理论,建立三重介质油藏水平井分形非线性渗流模型;基于有限元原理求解水平井动态压力,并对比各模型的压力动态曲线,总结渗流规律。在分析非线性参数、分形指数及水平井长度等相关参数的敏感性之后,将所建立模型进行实际井动态压力拟合并解释相关渗流参数,以期验证模型的准确性及实用价值。
1 缝洞型碳酸盐岩油藏渗流机理 1.1 基质非线性渗流将低渗储层微观渗流机理、边界层流动理论和毛细管渗流模型相结合,简化并改进非线性渗流模型。考虑边界层厚度与流体屈服应力值,在HagenPoisseuille定律的基础上进行修正[16]可得
| $ v = \frac{K}{\mu }{\left( {1 - \frac{\delta }{{{r_0}}}} \right)^4}\left[ {1 - \frac{{8{\tau _0}}}{{3{r_0}\left( {1 - \frac{\delta }{{{r_0}}}} \right)\nabla p}}} \right]\nabla p $ | (1) |
式中:v为通过岩心的流速,cm/s;K为岩心渗透率,mD;μ为流体黏度,mPa·s;r0为毛管半径,mm;δ为边界层厚度,mm;τ0为流体屈服应力,MPa;▽p为压力梯度,MPa/m。
对于相同毛管,δ/r0与压力梯度成反比[17],故假设δ/r0= a1/▽p;对于同一种流体,屈服应力值保持不变,假设8τ0/3r0=a2。将式(1)变形并简化可得
| $ v = \frac{K}{\mu }\left[ {1 - \frac{{4{a_1} + {a_2}}}{{\nabla p}} + \frac{{6a_1^2 + 3{a_1}{a_2}}}{{\nabla p\left( {\nabla p - {a_1}} \right)}}} \right]\nabla p $ | (2) |
式中:a1,a2均为实验拟合得到的常数值。
将表征多项式c1=4a1+a2, c2=a1, c3=6a12+3a1a2和条件"▽p=0时, v=0"代入式(2), 并约去c3, 得到简化后的模型为
| $ \begin{array}{l} v = \frac{K}{\mu }\left[ {1 - \frac{{{c_1}}}{{\nabla p}} - \frac{{{c_1}{c_2}}}{{\nabla p\left( {\nabla p - {c_2}} \right)}}} \right]\nabla p = \\ \;\;\;\;\;\frac{K}{\mu }\left( {1 - \frac{{{c_1}}}{{\nabla p - {c_2}}}} \right)\nabla p \end{array} $ | (3) |
式中:c1和c2是通过对实验数据进行非线性拟合得到的参数,c1反映了流体的屈服应力以及边界层对渗流的影响,c2反映了边界层对渗流的影响。
当c1=0时,式(3)简化为达西模型;当c2=0时,式(3)简化为拟启动压力梯度模型。c1/(▽p-c2)相当于启动压力梯度项。当v > 0时,▽p > c1 + c2,最小启动压力梯度为▽pmin = c1 + c2。启动压力梯度的存在与否以及取值大小均取决于c1,c2的值,即取决于矿场实际[18]。
1.2 裂缝分形特征利用分形维数及异常扩散系数来表征分形裂缝中的渗透率和孔隙度,能够精确地反映地下储层复杂的裂缝形态。设分形体内流体聚集在某节点处,且节点体积处处相等,则渗流节点的数量可结合节点密度求出,即
| $ \alpha = \frac{{{K_{{\rm{fw}}}}{{\left( {{D_{\rm{f}}}/{d_{\rm{s}}}} \right)}^2}}}{{{\varphi _{{\rm{fw}}}}\mu {C_{{\rm{ft}}}}r_{\rm{w}}^2}} $ | (4) |
式中:Df为分形维数;α为节点的数量;ds为谱维数;rw为井筒半径,m;Kfw为生产井处的渗透率,mD;φfw为生产井处的孔隙度;Cft为裂缝综合压缩系数,MPa-1。
考虑维数为d的欧氏空间内嵌入分形体,可得到用分形维数表征的孔隙度表达式为
| $ {\varphi _{\rm{f}}} = \frac{{{V_{\rm{f}}}}}{V} = \frac{{{V_{\rm{s}}}\alpha {r^{{D_{\rm{f}}} - 1}}\Delta r}}{{B\alpha {r^{d - 1}}\Delta r}} = \frac{{\alpha {V_{\rm{s}}}}}{B}{r^{{D_{\rm{f}}} - d}} $ | (5) |
式中:B为描述对称性的几何常量;V为储层总体积,m3;Vf为储层孔隙体积,m3;Vs为储集流体的节点体积,m3;r为距生产井的距离,m。
裂缝孔隙度主要受孔隙空间聚集方式(用分形维数表征)的影响,且与有效上覆压力呈指数关系,所以考虑应力敏感性的裂缝分形孔隙度表达式[19-20]为
| $ {\varphi _{\rm{f}}}(r) = {\varphi _{{\rm{fw}}}}\left( {\frac{r}{{{r_{\rm{w}}}}}} \right){r^{{D_{\rm{f}}} - d}}\exp \left[ { - {C_{\rm{f}}}\left( {{p_{\rm{i}}} - {p_{\rm{f}}}} \right)} \right] $ | (6) |
式中:Cf为裂缝孔隙压缩系数,MPa-1;pi为原始地层压力,MPa;pf为裂缝系统压力,MPa。
裂缝渗透率不仅取决于孔隙空间的聚集方式,还与裂缝之间的连通性(用异常扩散系数表征)密不可分。储层压力变化会引起裂缝张合状态的变化,从而影响储层渗透率,在对应力敏感地层不稳定试井的研究中发现,渗透率与基岩上覆压力之间也成指数关系。在分形孔隙度定义的基础上引入异常扩散系数便可得到考虑应力敏感性的分形渗透率[19-20],即
| $\begin{array}{l} {K_{\rm{f}}}(r) = {K_{{\rm{fw}}}}\left( {\frac{r}{{{r_{\rm{w}}}}}} \right){r^{{D_{\rm{f}}} - d - \theta }}\\ \exp \left[ { - {\alpha _{\rm{K}}}\left( {{p_{\rm{i}}} - {p_{\rm{f}}}} \right)} \right] \end{array} $ | (7) |
式中:αK为渗透率模数,MPa-1;θ为异常扩散系数。
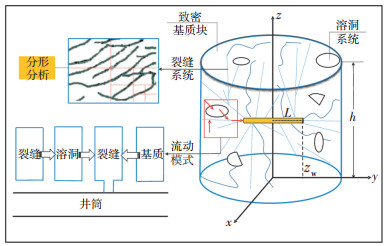
2 缝洞型碳酸盐岩分形油藏水平井非线性渗流模型 2.1 物理模型建立圆形三重介质碳酸盐岩分形油藏水平井物理模型[21](图 1),并设该模型符合以下假定条件:①模型由基质、裂缝和溶洞系统组成,基质块向裂缝和溶洞系统发生拟稳态窜流,溶洞系统向裂缝发生拟稳态窜流;②外边界为封闭或定压条件,储层厚度为h,原始压力为pi,水平井半长为L,水平井纵向深度为zw,油藏半径为re;③考虑储层的表皮系数、井筒储集系数以及裂缝渗透率的各向异性,裂缝系统水平渗透率为Kfh,垂直渗透率为Kfv,基质系统渗透率为Km,溶洞系统渗透率为Kv;④水平井位于油藏平面中心,产量为Q);⑤忽略重力与毛管压力的影响;⑥考虑裂缝系统的应力敏感性及裂缝的分形特征,基质向裂缝系统的窜流为非线性渗流。
|
下载eps/tif图 图 1 物理模型示意图 Fig. 1 Schematic diagram of the physical model |
在笛卡尔坐标系中,将流体流动的质量守恒方程和状态方程与非线性运动方程[式(3)]相结合,可得到缝洞型碳酸盐岩油藏水平井分形非线性渗流模型[22],即
| $ \begin{array}{*{20}{c}} {\frac{\partial }{{\partial {x_{\rm{D}}}}}\left( {r_{\rm{D}}^{{D_{\rm{f}}} - d - \theta }{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}}}}}\frac{{\partial {p_{{\rm{fD}}}}}}{{\partial {x_{\rm{D}}}}}} \right) + \frac{\partial }{{\partial {y_{\rm{D}}}}}\left( {r_{\rm{D}}^{{D_{\rm{f}}} - d - \theta }{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}}}}}\frac{{\partial {p_{{\rm{fD}}}}}}{{\partial {y_{\rm{D}}}}}} \right) + \frac{\partial }{{\partial {z_{\rm{D}}}}}\left( {L_{\rm{D}}^2{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}}}}}\frac{{\partial {p_{{\rm{fD}}}}}}{{\partial {z_{\rm{D}}}}}} \right) = }\\ {{\omega _{\rm{f}}}{{\left( {{h_{\rm{D}}}{L_{\rm{D}}}} \right)}^2}\frac{{\partial {p_{{\rm{fD}}}}}}{{\partial {t_{\rm{D}}}}} + {\lambda _{{\rm{mf}}}}{\delta _{{\rm{LVDf}}}}\left( {{p_{{\rm{fD}}}} - {p_{{\rm{mD}}}}} \right) + {\lambda _{{\rm{vf}}}}\left( {{p_{{\rm{fD}}}} - {p_{{\rm{vD}}}}} \right)} \end{array} $ | (8) |
| $ {\lambda _{{\rm{mf}}}}{\delta _{{\rm{LVDf}}}}\left( {{p_{{\rm{fD}}}} - {p_{{\rm{mD}}}}} \right) + {\lambda _{{\rm{mv}}}}{\delta _{{\rm{LVDv}}}}\left( {{p_{{\rm{vD}}}} - {p_{{\rm{mD}}}}} \right) = {\left( {{h_{\rm{D}}}{L_{\rm{D}}}} \right)^2}\left( {1 - {\omega _{\rm{f}}} - {\omega _{\rm{v}}}} \right)\frac{{\partial {p_{{\rm{mD}}}}}}{{\partial {t_{\rm{D}}}}} $ | (9) |
| $ {\lambda _{{\rm{vf}}}}\left( {{p_{{\rm{fD}}}} - {p_{{\rm{vD}}}}} \right) + {\lambda _{{\rm{mv}}}}{\delta _{{\rm{LVDv}}}}\left( {{p_{{\rm{vD}}}} - {p_{{\rm{mD}}}}} \right) = {\left( {{h_{\rm{D}}}{L_{\rm{D}}}} \right)^2}{\omega _{\rm{v}}}\frac{{\partial {p_{{\rm{vD}}}}}}{{\partial {t_{\rm{D}}}}} $ | (10) |
式中:rD为无因次渗流半径;LD为无因次水平井半长;hD为无因次储层厚度;tD为无因次时间;pfD为无因次裂缝压力;pmD为无因次基质压力;pvD为无因次溶洞压力;δLVDf为裂缝的无因次中间变量;δLVDv为溶洞的无因次中间变量;λmf为基质向裂缝窜流系数;λvf为溶洞向裂缝窜流系数;λmv为基质向溶洞窜流系数;ωf为裂缝弹性储能比;ωv为溶洞弹性储能比;下标D代表无因次;下标m,f,v分别代表基质、裂缝和溶洞系统。
若
初始条件:
| $ {p_{1{\rm{D}}}}\left( {{x_{\rm{D}}},{y_{\rm{D}}},{z_{\rm{D}}},{t_{\rm{D}}} = 0} \right) = 0\;\;\;\;(1 = {\rm{m}},{\rm{f}},{\rm{v}}) $ | (11) |
封闭外边界条件:
| $ {\left. {\frac{{\partial {p_{1{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right|_{{r_D} = {r_{{\rm{eD}}}}}} = {\left. {\frac{{\partial {p_{1{\rm{D}}}}}}{{\partial {z_{\rm{D}}}}}} \right|_{{z_D} = 0,1}} = 0 $ | (12) |
定压边界条件:
| $ {p_{1{\rm{D}}}}\left( {{r_{\rm{D}}} = {r_{{\rm{eD}}}}} \right) = {p_{1{\rm{D}}}}\left( {{z_{\rm{D}}} = 0,1} \right) = 0 $ | (13) |
内边界条件:
| $ \begin{array}{*{20}{c}} {{{\left. {\mathop {\lim }\limits_{{\varepsilon _{{\rm{D}} \to 0}}} \int_{{z_{{\rm{w}}0}} - \frac{{{\varepsilon _{\rm{D}}}}}{2}}^{{z_{{\rm{wD}}}} + \frac{{{\varepsilon _{\rm{D}}}}}{2}} {\left( {r_{\rm{D}}^{{D_{\rm{f}}} - d - \theta }{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}}}}}\frac{{\partial {p_{{\rm{fD}}}}}}{{\partial {r_{\rm{D}}}}}} \right)} {\rm{d}}{z_{{\rm{wD}}}}} \right|}_{{r_{\rm{D}}} = {\varepsilon _{\rm{D}}}}} = - \frac{1}{2},}\\ {\left| {{z_{\rm{D}}} - {z_{{\rm{wD}}}}} \right| \le \frac{{{\varepsilon _{\rm{D}}}}}{2}} \end{array} $ | (14) |
各无因次量定义如下:
对于缝洞型碳酸盐岩油藏水平井分形非线性渗流模型,首先采用隐式求解裂缝系统,应用Galerkin法,得到裂缝系统的有限元方程为
| $ \begin{array}{*{20}{c}} {\iiint\limits_{{\Omega _{\text{e}}}} {{N_i}\left[ {\frac{\partial }{{\partial {x_{\text{D}}}}}\left( {r_{\text{D}}^{{D_{\text{f}}} - d - \theta }{{\text{e}}^{ - {\alpha _{{\text{KD}}}}{p_{{\text{fD}}}}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {x_{\text{D}}}}}} \right) + \frac{\partial }{{\partial {y_{\text{D}}}}}\left( {r_{\text{D}}^{{D_{\text{f}}} - d - \theta }{{\text{e}}^{ - {\alpha _{{\text{KD}}}}{p_{{\text{fD}}}}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {y_{\text{D}}}}}} \right)} \right]{\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}\left[ {\frac{\partial }{{\partial {z_{\text{D}}}}}\left( {{{\text{e}}^{ - {\alpha _{{\text{KD}}}}{p_{{\text{fD}}}}}}L_{\text{D}}^2\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {z_{\text{D}}}}}} \right)} \right]{\text{d}}V} = } \\ {\iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}{\omega _{\text{f}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {t_{\text{D}}}}}{\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\delta _{{\text{LVDf}}}}{\lambda _{{\text{mf}}}}\left( {{p_{{\text{fD}}}} - {p_{{\text{mD}}}}} \right){\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\lambda _{{\text{vf}}}}\left( {{p_{{\text{fD}}}} - {p_{{\text{vD}}}}} \right){\text{d}}V}} \end{array} $ | (15) |
式中:Ni为形函数的分量,i=1,2,…,n。
以格林公式为基础,通过分部积分可得到内部单元和封闭条件外边界单元的有限元方程为
| $ \begin{array}{*{20}{c}} {\iiint\limits_{{\Omega _{\text{e}}}} {r_{\text{D}}^{{D_{\text{f}}} - d - \theta }{{\text{e}}^{ - {\alpha _{{\text{KD}}}}{p_{{\text{fD}}}}}}\left( {\frac{{\partial {N_i}}}{{\partial {x_{\text{D}}}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {x_{\text{D}}}}} + \frac{{\partial {N_i}}}{{\partial {y_{\text{D}}}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {y_{\text{D}}}}}} \right){\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{{\text{e}}^{ - {\alpha _{{\text{KD}}}}{p_{{\text{fD}}}}}}\left( {L_{\text{D}}^2\frac{{\partial {N_i}}}{{\partial {z_{\text{D}}}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {z_{\text{D}}}}}} \right){\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\delta _{{\text{LVDf}}}}{\lambda _{{\text{mf}}}}{p_{{\text{fD}}}}{\text{d}}V} + } \\ {\iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\lambda _{{\text{vf}}}}{p_{{\text{fD}}}}{\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}{\omega _{\text{f}}}\frac{{\partial {p_{{\text{fD}}}}}}{{\partial {t_{\text{D}}}}}{\text{d}}V} = \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\delta _{{\text{LVDf}}}}{\lambda _{{\text{mf}}}}{p_{{\text{mD}}}}{\text{d}}V} + \iiint\limits_{{\Omega _{\text{e}}}} {{N_i}{\lambda _{{\text{vf}}}}{p_{{\text{vD}}}}{\text{d}}V}} \end{array} $ | (16) |
由此可得,单元有限方程的矩阵形式为
| $ \begin{gathered} \iiint\limits_{{\Omega _{\text{e}}}} {\left[ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{GB}} + {\lambda _{{\text{mf}}}}\mathit{\boldsymbol{DN}}{\mathit{\boldsymbol{N}}^T} + {\lambda _{{\text{vf}}}}\mathit{\boldsymbol{EN}}{\mathit{\boldsymbol{N}}^T} + {\omega _{\text{f}}}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}\frac{{\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T}}}{{\Delta {t_{\text{D}}}}}} \right]{\text{d}}V\mathit{\boldsymbol{P}}_{\text{f}}^n} = \\ \iiint\limits_{{\Omega _{\text{e}}}} {{\omega _{\text{f}}}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}\frac{{\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T}}}{{\Delta {t_{\text{D}}}}}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{f}}^{n - 1}} + \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\iiint\limits_{{\Omega _{\text{e}}}} {{\lambda _{{\text{mf}}}}\mathit{\boldsymbol{DN}}{\mathit{\boldsymbol{N}}^T}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{m}}^{n - 1}} + \iiint\limits_{{\Omega _{\text{e}}}} {{\lambda _{{\text{vf}}}}\mathit{\boldsymbol{EN}}{\mathit{\boldsymbol{N}}^T}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{v}}^{n - 1}} \hfill \\ \end{gathered} $ | (17) |
假设E为单位矩阵,其他各矩阵的表达形式为
| $ \mathit{\boldsymbol{B}} = \left[ {\begin{array}{*{20}{l}} {\frac{{\partial {N_1}}}{{\partial {x_{\rm{D}}}}}}&{\frac{{\partial {N_2}}}{{\partial {x_{\rm{D}}}}}}& \cdots &{\frac{{\partial {N_n}}}{{\partial {x_{\rm{D}}}}}}\\ {\frac{{\partial {N_1}}}{{\partial {y_{\rm{D}}}}}}&{\frac{{\partial {N_2}}}{{\partial {y_{\rm{D}}}}}}& \cdots &{\frac{{\partial {N_n}}}{{\partial {y_{\rm{D}}}}}}\\ {\frac{{\partial {N_1}}}{{\partial {z_{\rm{D}}}}}}&{\frac{{\partial {N_2}}}{{\partial {z_{\rm{D}}}}}}& \cdots &{\frac{{\partial {N_n}}}{{\partial {z_{\rm{D}}}}}} \end{array}} \right],\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {{N_1}}\\ {{N_2}}\\ \vdots \\ {{N_n}} \end{array}} \right],{\mathit{\boldsymbol{P}}_{\rm{f}}} = \left[ {\begin{array}{*{20}{c}} {{p_{{\rm{fD}}1}}}\\ {{p_{{\rm{fD}}2}}}\\ \vdots \\ {{p_{{\rm{fD}}n}}} \end{array}} \right],{\mathit{\boldsymbol{P}}_{\rm{m}}} = \left[ {\begin{array}{*{20}{c}} {{p_{{\rm{mD}}1}}}\\ {{p_{{\rm{mD}}2}}}\\ \vdots \\ {{p_{{\rm{mD}}n}}} \end{array}} \right],{\mathit{\boldsymbol{P}}_{\rm{v}}} = \left[ {\begin{array}{*{20}{c}} {{p_{{\rm{vD1}}}}}\\ {{p_{{\rm{vD}}2}}}\\ \vdots \\ {{p_{{\rm{vD}}n}}} \end{array}} \right], $ |
| $\begin{array}{l} \mathit{\boldsymbol{C}} = \left[ {\begin{array}{*{20}{c}} {{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}1}}}}}&{}&{}&{}\\ {}&{{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{P_{{\rm{fD}}2}}}}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{{\rm{e}}^{ - {\alpha _{{\rm{KD}}}}{p_{{\rm{fD}}n}}}}} \end{array}} \right],\\ {\mathit{\boldsymbol{H}}_{\rm{A}}} = \left[ {\begin{array}{*{20}{c}} {{\delta _{{\rm{LVDA}}1}}}&{}&{}&{}\\ {}&{{\delta _{{\rm{LVDA}}2}}}&{}&{}\\ {}&{}& \ddots &{}\\ {}&{}&{}&{{\delta _{{\rm{LVDA}}n}}} \end{array}} \right]({\rm{A}} = {\rm{F}},{\rm{v}}),\\ \mathit{\boldsymbol{G}} = \left[ {\begin{array}{*{20}{c}} {r_{\rm{D}}^{{D_{\rm{f}}} - d - \theta }}&{}&{}&{}\\ {}&{r_{\rm{D}}^{{D_{\rm{f}}}} - d - \theta }&{}&{}\\ {}&{}&{L_{\rm{D}}^2}&{} \end{array}} \right] \end{array} $ |
对矩阵方程进一步简化可得
| $ {\mathit{\boldsymbol{K}}_{\rm{e}}}\mathit{\boldsymbol{P}}_{\rm{f}}^n = {\mathit{\boldsymbol{F}}_{\rm{e}}} $ | (18) |
其中Ke,Fe的表达形式为
| $ \begin{gathered} {K_{\text{e}}} = \iiint\limits_{{\Omega _{\text{e}}}} {\left[ {\mathit{\boldsymbol{C}}{\mathit{\boldsymbol{B}}^T}\mathit{\boldsymbol{GB}} + {\lambda _{{\text{mf}}}}{\mathit{\boldsymbol{H}}_{\text{f}}}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T} + {\lambda _{{\text{vf}}}}\mathit{\boldsymbol{EN}}{\mathit{\boldsymbol{N}}^T} + } \right.} \hfill \\ \;\;\;\;\;\;\;\left. {{\omega _{\text{f}}}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}\frac{{\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T}}}{{\Delta {t_{\text{D}}}}}} \right]{\text{d}}V \hfill \\ \end{gathered} $ | (19) |
| $ \begin{gathered} {\mathit{\boldsymbol{F}}_{\text{e}}} = \iiint\limits_{{\Omega _{\text{e}}}} {{\omega _{\text{f}}}{{\left( {{L_{\text{D}}}{h_{\text{D}}}} \right)}^2}\frac{{\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T}}}{{\Delta {t_{\text{D}}}}}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{f}}^{n - 1}} + \hfill \\ \;\;\;\;\;\;\;\iiint\limits_{{\Omega _{\text{e}}}} {{\lambda _{{\text{mf}}}}{\mathit{\boldsymbol{H}}_{\text{f}}}\mathit{\boldsymbol{N}}{\mathit{\boldsymbol{N}}^T}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{m}}^{n - 1}} + \hfill \\ \;\;\;\;\;\;\;\iiint\limits_{{\Omega _{\text{e}}}} {{\lambda _{{\text{vf}}}}\mathit{\boldsymbol{EN}}{\mathit{\boldsymbol{N}}^T}{\text{d}}V\mathit{\boldsymbol{P}}_{\text{v}}^{n - 1}} \hfill \\ \end{gathered} $ | (20) |
式中:Ke为非线性系数矩阵;Fe为单元载荷向量;上标n表示时刻变量。
式(18)为三重介质分形非线性模型裂缝系统的有限元单元平衡方程,同理可采用显式求解方法得到基质和溶洞系统的有限元单元平衡方程,且计算结果表明隐式求解裂缝系统、显式求解基质和溶洞系统的方法符合计算精度。
考虑到无限导流能力模型比均匀流量模型求解困难,通常选取0.7 L处为水平井在这2种模型下的等价压力点,从而可以借助均匀流量模型评价水平井井底压力。通过把水平井考虑成单元源汇项并积分,应用Delta函数将水平井划分成n个节点,并进行无因次化得到单元源汇项有限元方程。
所求压力解经过Laplace变换后,通过Duhamel原理引入井筒储集与表皮系数:
| $ {\bar p_{{\text{wD}}}} = \frac{{s{{\bar p}_{\text{D}}} + \frac{S}{{{L_{\text{D}}}}}}}{{s\left[ {1 + {C_{\text{D}}}s\left( {s{{\bar p}_{\text{D}}} + \frac{S}{{{L_{\text{D}}}}}} \right)} \right]}} $ | (21) |
式中:S为表皮因数;s为Laplace变量;CD为井筒储集系数。
采用Stehfest数值反演,得到考虑井筒储集效应与表皮因数的水平井无因次井底压力为
| $ {p_{{\text{wD}}}} = \frac{{\ln 2}}{{{t_{\text{D}}}}}\sum\limits_{i = 1}^N {{V_i}} {\bar p_{{\text{wD}}}} $ | (22) |
| $ {V_i} = {( - 1)^{\left( {\frac{N}{2} + i} \right)}}\sum\limits_{k = \frac{{i + 1}}{2}}^{\max \left[ {i,\frac{N}{2}} \right]} {\frac{{{k^{\frac{N}{2}}}(2k + 1)!}}{{(k + 1)!k!\left( {\frac{N}{2} - k + 1} \right)!(i - k + 1)!(2k - i + 1)!}}} $ | (23) |
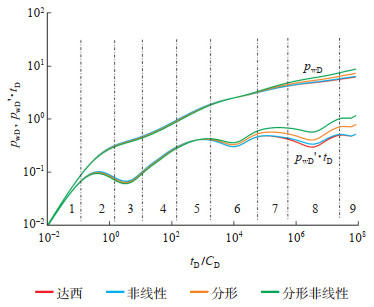
图 2为碳酸盐岩油藏水平井的达西、非线性以及分形非线性模型的压力动态曲线。各基本参数取值如下:CD= 100,S = 0,ωf = 0.01,ωv = 0.1,λmf= 0.001,λmv = 0.000 5,λvf = 0.1,LD = 5,hD = 200,αKD = 0.02。假设非线性参数cD= c1D= c2D,分形指数β = 2 + θ - Df,则各模型其他参数的取值如下:达西模型cD= 0,θ = 0,Df = 2;非线性流模型cD= 0.3,θ = 0,Df = 2;分形非线性模型cD = 0.5,θ = 0.3,Df = 1.9。在考虑储层应力敏感性的基础上,可以根据实际情况适当调整各模型的αKD值。
|
下载eps/tif图 图 2 不同模型压力动态曲线对比 1.井筒储存阶段;2.表皮效应过渡阶段;3.早期径向流阶段;4.早期线性流阶段;5.中期径向流阶段;6.溶洞-裂缝窜流阶段;7.溶洞-裂缝拟径向流阶段;8.基质-裂缝窜流阶段;9.系统拟径向流阶段 Fig. 2 Comparison of dynamic pressure curves of different models |
不同模型在不同流动阶段曲线的形态各异,但压力动态曲线仍然呈9个特征流动阶段(图 2)。以达西模型为例,具体流动阶段划分及不同流动阶段压力动态曲线特征[23-24]如表 1所列。通过分析和对比非线性、分形非线性模型的压力动态曲线与达西模型的压力动态曲线的异同点(图 2)可发现,非线性参数主要影响基质-裂缝窜流强度,而分形指数使得溶洞-裂缝窜流后的流动阶段的压力动态曲线发生上翘。
|
|
下载CSV 表 1 不同流动阶段压力动态曲线特征 Table 1 Characteristics of dynamic pressure curves in different flow stages |
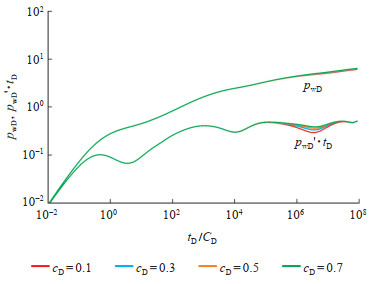
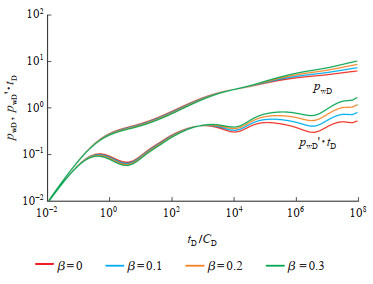
首先对非线性参数和分形指数进行敏感性分析,各基本参数取值如下:CD = 100,S = 0,ωf = 0.1,ωv = 0.5,λm = 0.001,λv = 0.1,LD = 5,hD = 200,αKD = 0.02。图 3与图 4分别为非线性参数cD和分形指数β对压力动态曲线的影响。
|
下载eps/tif图 图 3 非线性参数对压力动态曲线的影响 Fig. 3 Effect of nonlinear parameters on dynamic pressure curves |
|
下载eps/tif图 图 4 分形指数对压力动态曲线的影响 Fig. 4 Effect of fractal index on dynamic pressure curves |
非线性参数主要对基质向裂缝的窜流段有显著影响,基本不影响溶洞向裂缝系统的窜流段。随着非线性参数的增大,基质向裂缝的窜流强度减弱,持续时间变短。在压力导数曲线上表现为第2个下凹段延迟出现,下凹程度减弱,但窜流段结束的时间不受影响。
分形指数对压力动态曲线的影响主要体现在溶洞向裂缝窜流后的流动阶段,而对早期径向流和早期线性流阶段只产生微小的影响。从溶洞-裂缝拟径向流阶段开始,压力及其导数曲线随着时间的增加而逐渐上翘,且上翘幅度随着分形指数的增大而加剧。分形指数并不影响各个窜流段出现的时间以及窜流强度,所以压力导数曲线上下凹段的深度和持续时间均保持不变。
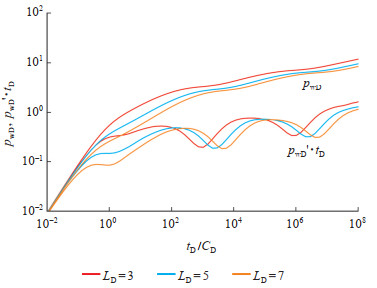
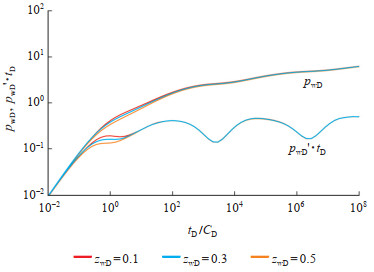
图 5与图 6分别为水平井长度LD和纵向位置zwD对压力动态曲线的影响,各基本参数取值如下:CD = 100,cD= 0,β = 0.1,S = 0,ωf = 0.01,ωv = 0.1,λm= 0.001,λv= 0.1,hD= 200,αKD= 0.02。研究表明,水平井越长,压力及其导数曲线越低,早期径向流越明显,从而后续流动阶段出现的时间延迟。当水平井长度小到一定程度时,早期径向流易被井筒储集效应所掩盖。考虑储层分形和应力敏感性特征,不同长度水平井的压力动态曲线并不在后期汇聚在一起,而是呈平行分布。在其他参数不变的情况下,水平井越靠近油层中部,即zwD的值越接近0.5,早期径向流阶段出现得越早,同时早期线性流持续时间越长,但水平井纵向上位置的变化并不影响其他流动阶段。
|
下载eps/tif图 图 5 水平井长度对压力动态曲线的影响 Fig. 5 Effect of horizontal well length on dynamic pressure curves |
|
下载eps/tif图 图 6 水平井纵向位置对压力动态曲线的影响 Fig. 6 Effect of horizontal well position on dynamic pressure curves |
为了验证本文模型的正确性,进一步认识具有分形特征的缝洞型碳酸盐岩油藏的渗流特征,对四川CN油田S63井的渗流参数进行了解释。为了便于试井解释,假定裂缝垂向渗透率与水平渗透率相等,即β = 1。S63井的基础参数取值如表 2所列。
|
|
下载CSV 表 2 S63井基础参数取值 Table 2 Values of basic parameters of well S63 |
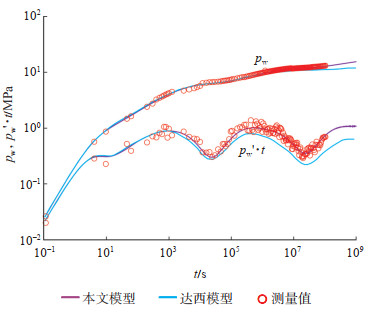
各个模型的异同已在渗流规律及敏感性分析部分进行了详细对比,但为方便对比、分析本文分形非线性模型的合理性,同时应用达西模型和本文模型进行试井拟合(图 7)。2个模型的拟合结果均显示压力导数与压力曲线分开。实际压力导数曲线和理论曲线在前期拟合程度相对较低,这是由于实际储层的井筒储集系数发生变化所导致的,在实际试井过程中普遍存在类似的问题。在渗流的中后期,虽然实测数据不完整,压力导数曲线仍明显出现反映孔洞缝三重介质储层渗流特征的2个下凹段,且相对于达西模型,本文模型的拟合结果更加精确,理论计算值和实测值拟合得更好。选取本文的分形非线性模型进行S63井的试井解释,表 3为该模型所解释的渗流参数。
|
下载eps/tif图 图 7 实际算例压力动态拟合曲线 Fig. 7 Dynamic pressure fitting curves of the actual example |
|
|
下载CSV 表 3 S63井渗流参数解释 Table 3 Explanation of seepage parameters of well S63 |
实际生产曲线的基质向裂缝的窜流段明显比达西模型所呈现的下凹程度小,且试井解释下的非线性参数为0.15,基质渗透率为1.52 mD,这都体现了基质确实存在非达西渗流。拟合结果表明,采用本文模型进行渗流参数解释更加精确,这说明储层考虑分形特征和非线性渗流后更符合油井的实际情况,可应用本文的分形非线性模型进行实际试井解释及渗流规律分析。
6 结论(1)引入分形理论描述裂缝系统的分形特征,同时应用非线性渗流新模型描述致密基质块的渗流特征,在此基础上建立缝洞型油藏水平井分形非线性渗流模型,并基于有限元方法求解水平井动态压力。
(2)通过对比达西模型与分形非线性模型的异同点,总结缝洞型碳酸盐岩油藏水平井的渗流规律,分析各个流动阶段的特点,将渗流过程划分为9个流动阶段,即井筒储存、表皮效应过渡、早期径向流、早期线性流、中期径向流、溶洞向裂缝窜流、溶洞-裂缝拟径向流、基质向裂缝窜流以及系统拟径向流。
(3)非线性参数主要影响基质向裂缝系统的窜流段,随着非线性参数的增大,基质向裂缝系统窜流强度减小,持续时间变短。分形指数不影响窜流出现的时间及强度,它对压力动态曲线的影响主要体现在溶洞向裂缝窜流后的阶段,压力及导数曲线随时间增加而逐渐上翘,且上翘幅度随分形指数的增大而加剧。
(4)利用本文的分形非线性模型进行实际井动态压力拟合并解释相关渗流参数,考虑了储层分形特征和非线性渗流后,模型更贴近矿场实际,可用其进行实际试井解释及渗流规律分析。
| [1] |
葛家理, 吴玉树. 裂-隙油藏井底定压生产动态特征与不稳定试井分析方法. 石油勘探与开发, 1982(3): 53-65. GE J L, WU Y S. The behavior of naturally fractured reservoirs and the technique for well test analysis at constant pressure conduction. Petroleum Expoloration and Development, 1982(3): 53-65. |
| [2] |
易定红, 王建功, 石兰亭, 等. 柴达木盆地英西地区E32碳酸盐岩沉积演化特征. 岩性油气藏, 2019, 31(2): 46-55. YI D H, WANG J G, SHI L T, et al. Sedimentary evolution chara-cteristics of E 32 carbonate rocks in Yingxi area, Qaidam Basin. Lithologic Reservoirs, 2019, 31(2): 46-55. |
| [3] |
葛小波, 李吉君, 卢双舫, 等. 基于分形理论的致密砂岩储层微观孔隙结构表征:以冀中坳陷致密砂岩储层为例. 岩性油气藏, 2017, 29(5): 106-112. GE X B, LI J J, LU S F, et al. Fractal characteristics of tight sandstone reservoir using mercury intrusion capillary pressure:a case of tight sandstone reservoir in Jizhong Depression. Lithologic Reservoirs, 2017, 29(5): 106-112. DOI:10.3969/j.issn.1673-8926.2017.05.012 |
| [4] |
刘化普, 刘慧卿, 王敬. 缝洞型三重介质油藏分形渗流规律. 新疆石油地质, 2017, 38(2): 204-208. LIU H P, LIU H Q, WANG J. Fractal percolation law in fractured-vuggy triple medium reservoirs. Xinjiang Petroleum Geology, 2017, 38(2): 204-208. |
| [5] |
李松泉, 程林松, 李秀生, 等. 特低渗透油藏非线性渗流模型. 石油勘探与开发, 2008, 35(5): 606-612. LI S Q, CHENG L S, LI X S, et al. Non-linear seepage flow models of ultra-low permeability reservoirs. Petroleum Exploration and Development, 2008, 35(5): 606-612. DOI:10.3321/j.issn:1000-0747.2008.05.013 |
| [6] |
姚军, 戴卫华, 王子胜. 变井筒储存的三重介质油藏试井解释方法研究. 石油大学学报(自然科学版), 2004, 28(1): 46-51. YAO J, DAI W H, WANG Z S. Well test interpretation method for triple medium reservoir with variable wellbore storage. Journal of the University of Petroleum, China(Edition of Natural Science), 2004, 28(1): 46-51. DOI:10.3321/j.issn:1000-5870.2004.01.013 |
| [7] |
CAMACHO-VELAZQUEZ R, VASQUEZ-CRUZM, CASTREJONAIVAR R, et al. Pressure transient and decline curve behaviors in naturally fractured vuggy carbonate reservoirs. SPE 77689, 2002.
|
| [8] |
李成勇, 刘启国, 张燃, 等. 三重介质油藏水平井试井解释模型研究. 西南石油学院学报, 2006, 28(4): 32-35. LI C Y, LIU Q G, ZHANG R, et al. The research of well test of horizontal well in triple medium reservoir. Journal of Southwest Petroleum Institute, 2006, 28(4): 32-35. DOI:10.3863/j.issn.1674-5086.2006.04.009 |
| [9] |
张冬丽, 李江龙, 吴玉树. 缝洞型油藏三重介质数值试井模型影响因素. 西南石油大学学报(自然科学版), 2010, 32(6): 113-120. ZHANG D L, LI J L, WU Y S. Influencing factors of the numerical well test model of the triple-continuum in fractured vuggy reservoir. Journal of Southwest Petroleum University (Science & Technology Edition), 2010, 32(6): 113-120. DOI:10.3863/j.issn.1674-5086.2010.06.023 |
| [10] |
GOMEZ S, FUENTES G, CAMACHO R, et al. Application of an evolutionary algorithm in well test characterization of naturally fractured vuggy reservoirs. SPE 103931, 2006.
|
| [11] |
LI Y, WANG Q, LI B Z, et al. Dynamic characterization of different reservoir types for a fractured-caved carbonate reservoir. SPE 188113, 2017.
|
| [12] |
CHANG J, YORTSOS Y C. Pressure transient analysis of fractal reservoirs. SPE Formation Evaluation, 1990, 5(1): 31-38. DOI:10.2118/18170-PA |
| [13] |
ACUNAJ A, ERSHAGHⅡ, YORTSOS Y C. Practical application of fractal pressure-transient analysis of naturally fractured reservoirs. SPE Formation Evaluation, 1995, 10(3): 173-179. DOI:10.2118/24705-PA |
| [14] |
RAZMINIA K, RAZMINIA A, TRUJILO J. Analysis of radial composite systems based on fractal theory and fractional calculus. Signal Processing, 2015, 107: 378-388. DOI:10.1016/j.sigpro.2014.05.008 |
| [15] |
张本健, 曹建, 邓清源, 等. 基于树状分形网络的裂缝性气藏试井模型. 西南石油大学学报(自然科学版), 2018, 40(6): 110-118. ZHANG B J, CAO J, DENG Q Y, et al. A model of wells testing in fractured gas reservoirs based on tree fractal network. Journal of Southwest Petroleum University(Science & Technology Edition), 2018, 40(6): 110-118. |
| [16] |
姜瑞忠, 李林凯, 徐建春, 等. 低渗透油藏非线性渗流新模型及试井分析. 石油学报, 2012, 33(2): 264-268. JIANG R Z, LI L K, XU J C, et al. A nonlinear mathematical model for low-permeability reservoirs and well-testing analysis. Acta Petrolei Sinica, 2012, 33(2): 264-268. |
| [17] |
徐绍良, 岳湘安, 侯吉瑞. 去离子水在微圆管中流动特性的实验研究. 科学通报, 2007, 52(1): 120-124. XU S L, YUE X A, HOU J R. Experimental study on flow characteristics of deionized water in micro-circular tubes. Chinese Science Bulletin, 2007, 52(1): 120-124. DOI:10.3321/j.issn:0023-074X.2007.01.020 |
| [18] |
张春光, 姜瑞忠, 乔欣, 等. 双重介质致密分形气藏水平井压力动态分析. 东北石油大学学报, 2018, 42(6): 95-103. ZHANG C G, JIANG R Z, QIAO X, et al. Transient pressure analysis of the horizontal well in dual-medium tight fractal gas reservoirs. Journal of Northeast Petroleum University, 2018, 42(6): 95-103. DOI:10.3969/j.issn.2095-4107.2018.06.010 |
| [19] |
官庆. 利用分形理论建立压力敏感地层双重介质分形油藏的模型研究. 成都: 西南石油大学, 2007. GUAN Q. Research of pressure sensitive dual porosity fractal reservoir model built with fractal theory. Chengdu: Southwest Petroleum University, 2007. |
| [20] |
刘航宇, 田中元, 徐振永. 基于分形特征的碳酸盐岩储层孔隙结构定量评价. 岩性油气藏, 2017, 29(5): 97-105. LIU H Y, TIAN Z Y, XU Z Y. Quantitative evaluation of carbonate reservoir pore structure based on fractal characteristics. Lithologic Reservoirs, 2017, 29(5): 97-105. DOI:10.3969/j.issn.1673-8926.2017.05.011 |
| [21] |
程时清, 屈雪峰. 三重介质模型试井分析方法. 油气井测试, 1997, 6(1): 5-11. CHENG S Q, QU X F. Well testing analysis method for the triple porosity reservoir. Well Testing, 1997, 6(1): 5-11. |
| [22] |
杨明. 低渗透油藏试井解释方法研究. 青岛: 中国石油大学(华东), 2013. YANG M. Study of well test interpretation method in low permeability oil reservoir. Qingdao: China University of petroleum (East China), 2013. |
| [23] |
孟凡坤, 雷群, 何东博, 等. 三孔均质复合碳酸盐岩气藏斜井试井解释模型. 新疆石油地质, 2018, 39(5): 591-596. MENG F K, LEI Q, HE D B, et al. Well test interpretation model for deviated wells in tri-porosity-media and homogeneous composite carbonate gas reservoirs. Xinjiang Petroleum Geology, 2018, 39(5): 591-596. |
| [24] |
姜瑞忠, 沈泽阳, 崔永正, 等. 双重介质低渗油藏斜井压力动态特征分析. 岩性油气藏, 2018, 30(6): 131-137. JIANG R Z, SHEN Z Y, CUI Y Z, et al. Dynamic characteristics analysis of inclined well pressure in dual medium low permeability reservoir. Lithologic Reservoirs, 2018, 30(6): 131-137. |
 2019, Vol. 31
2019, Vol. 31



