2. 兰州财经大学 统计学院, 兰州 730020;
3. 中国石油勘探开发研究院, 北京 100083
2. Lanzhou University of Finance and Economics, Lanzhou 730020, China;
3. PetroChina Research Institute of Petroleum Exploration&Development, Beijing 100083, China
非常规致密烃源岩的分布和致密油气息息相关,致密油气预测的一项重要内容是准确预测有效烃源岩分布[1]。石油勘探中,表征烃源岩有机质丰度的一个重要指标是总有机碳(Total organic carbon,TOC)含量,即单位质量岩石中有机碳的百分数[2]。目前利用地球物理技术预测TOC最为准确的是实验岩石物理分析与建模[3],受岩心取样成本高和应用条件苛刻所限,其更多地停留在理论研究阶段。近年来,随着非常规油气勘探技术的发展,基于试验或计算的TOC岩石物理分析技术得到关注[4],很好地验证了已有井解释模型的可靠性。目前应用最多且适用条件宽泛的技术是基于测井曲线的TOC估算技术,面向不同的地质沉积特征,形成了不同的单测井曲线估算和多测井曲线加权估算技术[5-8]。如何将井上估算结果与地震数据有机结合,是地球物理技术预测TOC在地层空间分布的最大制约因素,其关键在于如何准确地获得对TOC敏感的弹性参数。目前采取的手段主要包括交会分析、神经网络训练等,即利用岩心实测或测井曲线估算的TOC与弹性参数拟合,由拟合关系将地震反演敏感参数转换成TOC含量的空间分布[9-13]。
这些技术已经在非常规页岩油气和致密油气地球物理预测中发挥着作用,但是在应用中仍然存在很多问题。一是致密油气具有超低孔、低渗及岩性配置复杂的特征,实验岩石物理分析中往往样点数目不够,实际生产中的适用性受限。二是由于岩性配置复杂及“源储一体”的特征,使基于测井曲线的TOC估算结果误差较大,常规估算方法得到的TOC曲线精度不高,存在与样点实验观测值匹配度低等问题。三是由于致密油气具有“短排短运”的特性,有机质空间分布具有“大分散、小聚集”的特征,非均质性强,基于敏感属性反演间接预测TOC空间分布的难度大。
借鉴已有技术思路,笔者提出一种基于最优化估算和贝叶斯统计分类的TOC井-震联合预测技术。其充分利用实验室观测数据和测井数据构建模型,利用最优化算法求取井点最优估算的TOC曲线,在TOC敏感参数反演的基础上,利用贝叶斯统计分类方法得到TOC空间概率分布,以期该技术应用于湖相致密泥灰岩预测,为高产油井部署提供依据。
1 基于最优化算法的TOC曲线估算该项技术是对常规测井曲线拟合得到的TOC曲线的校正,以求得准确的TOC曲线。
首先须要获得必需的实验室观测数据。这需要实验室测定的岩样体积及质量、XRD和TOC测量值。另外须要获得研究层段流体密度、孔隙度等参数。如果缺失实验室观测数据,则须要利用常规测井曲线估算得到。
利用实验室数据可以构建理论上的矿物岩石骨架模型,模型中将黏土和无机矿物含量统一为岩石骨架,TOC为有机矿物成分。据此,可以将实验室数据和测井曲线关联,建立一个包含TOC的响应方程
| $ \begin{array}{l} \rho = \left[ {(1 - K){\rho _{{\rm{nk}}}} + K{\rho _{{\rm{TOC}}}}} \right](1 - \varphi ) + \;\\ \;\;\;\;\;\;\left[ {{\rho _{\rm{o}}}\left( {1 - {S_{\rm{w}}}} \right) + {\rho _{\rm{w}}}{S_{\rm{w}}}} \right]\varphi \end{array} $ | (1) |
式中:ρ为响应方程计算的岩石体密度理论值,g/cm3;ρnk为无机矿物密度,g/cm3;ρo为油密度,g/cm3;ρw为水密度,g/cm3;ρTOC为干酪根密度,g/cm3;φ为总孔隙度,%;Sw为含水饱和度,%;K为干酪根体积分数,%。
实验室测量可以得到油密度和水密度;实验室测量或测井曲线计算可得到孔隙度和含水饱和度。由TOC观测值和实验室岩样数据计算得到无机矿物密度和干酪根密度,通常求取样点平均值作为常数参与方程计算。研究中利用如下公式计算无机矿物密度和TOC密度
| $ {Q_{{\rm{nk}}}} = Q - {Q_{{\rm{TOC}}}}, {\rho _{{\rm{nk}}}} = \frac{{{Q_{{\rm{nk}}}}}}{V}, {\rho _{{\rm{TOC}}}} = \frac{{{Q_{{\rm{TOC}}}}}}{V} $ | (2) |
式中:Q为干岩样的质量,g;Qnk为无机矿物质量,g;QTOC为TOC质量,g;V为干岩样的体积,cm3。
实际生产中,这些数据在实验室都可获得。
由于K的不确定性,因此在计算ρ时须要消除参数K。假定TOC含量初始估算值用C表示,则
| $ C = \frac{{K(1 - \varphi ){\rho _{{\rm{TOC}}}}}}{\rho }, \;{\rm{因此}}K = \frac{{C\rho }}{{(1 - \varphi ){\rho _{{\rm{TOC}}}}}} $ | (3) |
将式(3)代入式(1)得
| $ \rho = \frac{{{\rho _{{\rm{TOC}}}}\left[ {(1 - \varphi ){\rho _{{\rm{nk}}}} + \left( {{\rho _{\rm{o}}} - {\rho _{\rm{o}}}{S_{\rm{w}}} + {\rho _{\rm{w}}}{S_{\rm{w}}}} \right)\varphi } \right]}}{{{\rho _{{\rm{TOC}}}} + C\left( {{\rho _{{\rm{nk}}}} - {\rho _{{\rm{TOC}}}}} \right)}} $ | (4) |
为了使ρ与测井获得的密度ρb无限靠近,须要给定C一个初始数值。实际计算中,C可以由实验室样点TOC测量值与敏感测井曲线拟合得到,即初始TOC曲线值。在此基础上,利用最优化算法迭代估算,使校正后TOC与实验室样点TOC测量值匹配最佳。这里采用共轭梯度法进行最优化估算。最优化计算中目标函数设定为
| $ \min F(C) = \min {\left( {\rho - {\rho _{\rm{b}}}} \right)^2} + g(C) $ | (5) |
式中:F (C)为目标函数;g (C)为约束项。
通过约束项可以使目标函数达到极小值。目的层段实验室测定TOC值在[0, 4]内,因此约束条件设为0 ≤ x ≤ 4,则约束项可以表示为
| $ g(C) = {10^6}{[|C| - C]^2} + {10^6}{[|4 - C| - (4 - C)]^2} $ | (6) |
当优化计算的C不满足约束条件时,约束项将是一个非常大的数值,使得目标函数不能达到极小值。
2 基于贝叶斯统计的TOC概率体计算贝叶斯统计方法可以充分利用所有可能的信息,综合利用岩石物理和测井先验信息、样本信息,将地震属性数据看成是一个随机变量,进行后验概率密度统计,很好地将小、中尺度分析结果应用于大尺度地震预测,大大降低预测误差[14]。贝叶斯统计通过核密度估计方法进行判别分类,相当于二维属性样点被映射到三维空间,由一个二维曲面将叠置区域TOC值样点区分开来。
基于贝叶斯统计的TOC概率体计算,前提是通过分析已经得到TOC的敏感参数,依据最优化估算的TOC曲线,设定阈值,可将TOC划分为高、中、低3类。在此基础上,针对反演的TOC敏感参数,利用如下公式开展TOC概率体计算
| $ P\left( {{c_i}|X} \right) = \frac{{P\left( {X|{c_{\rm{i}}}} \right)P\left( {{c_{\rm{i}}}} \right)}}{{\sum\limits_{i = 1}^M P \left( {X|{c_{\rm{i}}}} \right)P\left( {{c_{\rm{i}}}} \right)}} $ | (7) |
式中:M为岩性分类数,本例中等于3;ci为TOC划分3类中的某一类;X为样本点,带有多种属性,即多个TOC敏感参数;P (ci)为3类TOC分布的先验信息,由样本中该类TOC样本数占总样本数比例而定;P (X|ci)为条件概率,指假定是ci所指TOC类型情况下属性样点X的分布概率密度;P (c|Xi)为后验条件概率,指给定的属性样点判别为某一类TOC的概率。因此,针对每一个样点,计算结果有3个,分别代表了3类TOC概率的大小。
由于P (ci)是已知的,所以求取P (c|Xi)的关键是估算P (X|ci)的分布。这里采用Epanechnikov核函数进行核密度估计
| $ K(x) = \left\{ {\begin{array}{*{20}{l}} {\frac{3}{4}\left( {1 - {x^2}} \right), }&{|x| \le 1}\\ 0&{{\rm{其他}}} \end{array}} \right. $ | (8) |
式中:K (x)为核密度估计值;x为样点到中心点的欧氏距离。
贝叶斯分类是将低维空间线性不可分的点通过非线性方式映射到高维空间进行区分,这使得运算量呈指数增长。核函数通过内积运算的方式进行降维,在确保结果精度的同时大大减少了计算量。因为与Gaussian核函数等相比较,Epanechnikov核函数在置信区间外的值为零,因此其估计的分布更加精确。依据估计的P (X|ci)分布,可以计算P (c|Xi)的后验概率分布,最终判别TOC敏感属性在不同取值范围时,TOC类型归属概率的大小。
3 应用实例 3.1 束鹿凹陷烃源岩特征束鹿凹陷位于渤海湾盆地束鹿地区,为一个东断西超、北东走向的狭长单断箕状凹陷,在陡侧和缓坡带广泛沉积了多期叠置的砾岩体,洼槽则沉积了巨厚的泥灰岩。目的层沙河子组下亚段泥灰岩有机质丰度高,特别是有机碳含量高;同时泥灰岩有机质类型好,主要为Ⅱ型干酪根,转化率高、排烃能力强,为优质烃源岩;厚度大于200 m的泥灰岩分布面积约200 km2,油气资源丰富,勘探潜力大。
沙三下亚段尽管沉积了巨厚的泥灰岩,但其分布具有如下特征:①纵向上与砂岩、砾岩形成互层或薄互层,岩性配置复杂;②泥灰岩具有“自生自储”的特征,有机碳分布具有“大分散、小聚集”的特征。
3.2 测井解释方法对比分析,获得初始TOC曲线在具有较全的常规测井曲线和TOC样点测量的前提下,利用不同的测井解释方法估算TOC曲线,并对估算结果进行对比分析,获得一条初始的井上TOC曲线。常规思路中,这条曲线将作为井上TOC估算的最终结果。本研究将这条曲线作为输入,参与后续的基于岩石物理模型的TOC最优化估算。
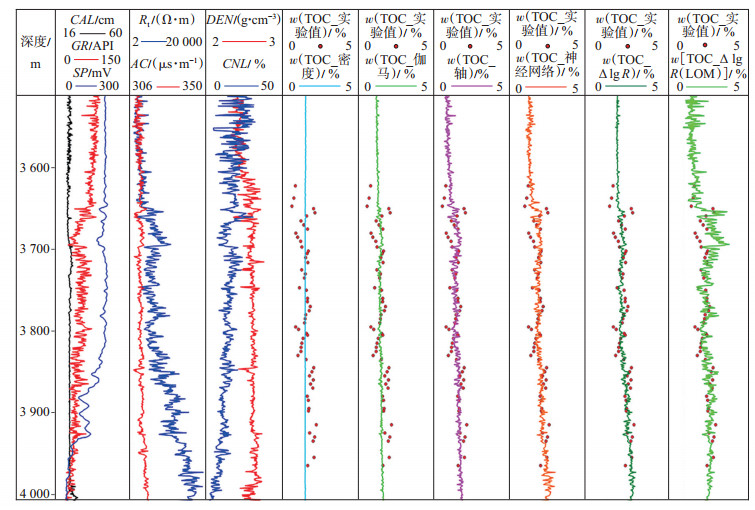
研究中开展了基于单测井和多测井曲线拟合的算法估算TOC曲线,并利用验证井对不同算法的TOC估值进行对比(图 1)。这里采用密度拟合、自然伽马拟合、铀元素拟合、神经网络训练、Δlg R线性拟合、Δlg R_LOM拟合等6种算法分别估算得到1条TOC初始曲线,分别命名为TOC_密度、TOC_伽马、TOC_铀、TOC_神经网络、TOC_ΔlgR和TOC_ΔlgR_LOM。估算结果分别与验证井目的层岩样TOC拟合分析,认为Δlg R_LOM算法最优,其估算值与样点TOC测量值吻合度最高。由于Δlg R_LOM算法中LOM反映了有机质成熟度,与层段烃源岩的埋藏史和热演化史等相关,在相关数据不全的情况下,可通过实测TOC值反演出LOM值,与深度建立关系后引入TOC校正项,对全井段的TOC进行预测。尽管Δlg R_LOM算法估算结果较好,但与真实值仍然存在较大误差,这在后续的井-震联合预测中会放大误差,因此须进一步校正。
|
下载原图 图 1 某井多种方法估算的TOC值对比 Fig. 1 Comparison of TOC values estimated by various methods of a well |
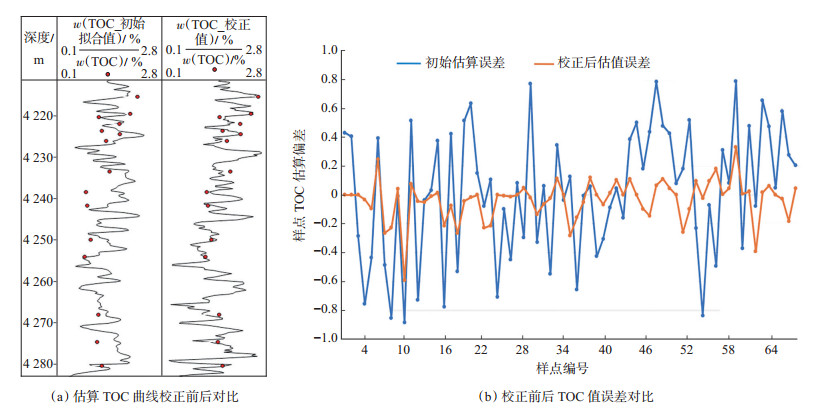
利用建立的岩石物理模型,通过最优化迭代寻优后,TOC初始估算值得到了很好地校正。Δlg R_ LOM方法估算的初始TOC与岩石物理模型校正后的TOC总体分布趋势一致[图 2(a)],但局部细节变化较大,与样点TOC更加吻合,在局部具有很好的对应性;与岩心样点真实测量值相比,校正后的TOC值误差更小[图 2(b)],证明了岩石物理模型校正后的TOC曲线可有效地应用于后续的TOC空间分布预测。
|
下载原图 图 2 基于测井岩石物理模型和最优化算法得到校正后的TOC Fig. 2 Corrected TOC based on log rock physical model and optimization algorithm |
考虑矿物成分对TOC含量影响大,选用实验室XRD数据和岩心TOC测量数据构建岩石物理量版。基于XRD数据开展岩石物理TOC分析的优点是:①基于矿物组分构建的岩石物理模型可以很好地分析TOC与弹性参数的关系;②XRD数据参与测井评价模型的构建有助于提高测井解释结果的准确度。
XRD测定的各种矿物的含量可以用体积分数或质量分数来表示,本文中涉及的数据来源于油田,其用体积分数表示,实验室测量提供了矿物成分弹性模量参考值。考虑到致密岩性的特征,在模型构建中首先使用文献[15]所述的Hashin-Shtrikman界限计算岩石骨架体积模量与剪切模量,与Reuss,Voigt等界限相比较,这种界限估算的岩石骨架弹性模量范围更小,因此更加精确;其次利用K-T公式[15]计算干岩石体积模量与剪切模量,其优势在于其适用于致密岩性低孔隙度的条件;然后利用Gassmann方程计算饱和水岩石体积模量与剪切模量,最后得到基于矿物成分等效介质模型计算的岩石弹性参数。
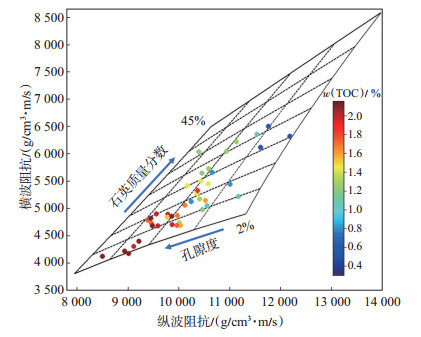
图 3为用3口井实验室数据建立的TOC量版,色标显示的是样点TOC观测值。XRD数据显示泥灰岩骨架矿物是方解石和白云石,质量分数为50%~70%;其次是黏土和石英(包括长石)矿物,其他矿物成分(刚玉、黄铁矿、沸石等)占比很小,质量分数不到10%。实验室分析认为有机质丰度与黏土矿物含量相关,同时石英含量远小于岩石骨架含量,这很好地解释了量版中TOC随石英含量增加而减少的原因。泥灰岩储集空间主要为溶蚀孔(有机质孔)、晶间孔和纹层缝,随着TOC含量增加会形成更多的有机质孔,反映了致密泥灰岩中TOC含量高、孔隙度相对较大的特征。随着黏土含量和孔隙度的增大,纵、横波速度降低,致密岩性密度微弱减小,因此纵、横波阻抗随TOC含量增大而减小。
|
下载原图 图 3 TOC岩石物理量版 Fig. 3 TOC quantitative edition of petrophysics |
实验室岩石物理TOC量版(图 3)显示,纵、横波阻抗可以较好地区分TOC大小。在计算得到更加准确的TOC曲线后,开展测井尺度TOC敏感参数分析,这是验证实验岩石物理结果的可用性和地震宏观尺度预测TOC空间分布的纽带。在已知纵波速度、横波速度和密度曲线的前提下,可计算井上纵、横波阻抗,开展测井岩石物理分析。
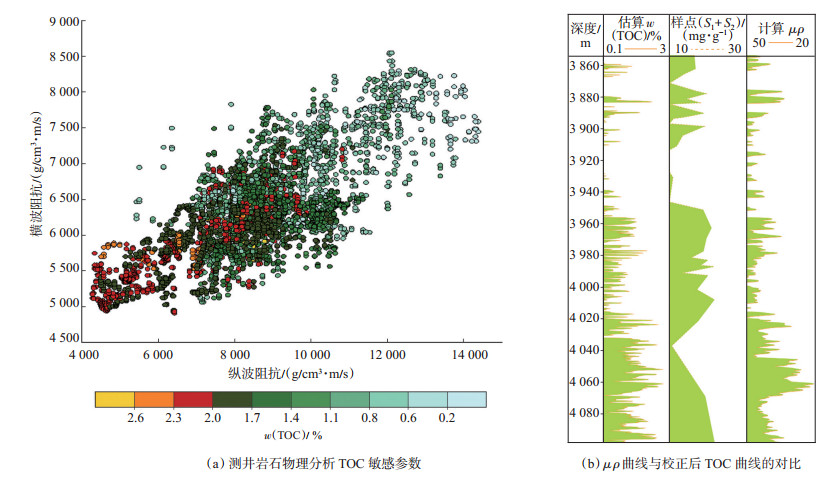
研究选取目的层段250 m厚度,0.125 m采样数据进行测井岩石物理交会分析,样本值为最优化计算校正后的TOC。结果显示[图 4(a)],在大样本情况下,纵、横波阻抗仍然可以较好地区分TOC。与实验岩石物理量版显示结果一样,纵、横波阻抗越小,TOC值总体越大。针对目的层段,分析认为TOC质量分数大于2.0%时指示有效烃源岩或者含油气储层(红色及棕黄色显示)。为了说明可行性,利用和横波阻抗直接相关的弹性属性参数μ ρ与最优化校正TOC曲线以及实验室样点总排烃量S1 + S2插值后的曲线进行对比[图 4(b)],良好的对应性说明可以利用纵、横波阻抗开展TOC的空间分布预测。测井TOC敏感参数交会和TOC岩石物理量版分析具有相同的结果,即纵、横波阻抗随TOC含量增大而减小。
|
下载原图 图 4 测井岩石物理分析TOC敏感参数及对比 Fig. 4 sensitive parameters and their contrast in logging petrophysics analysis |
须要说明的是,可以看到测井岩石物理分析结果对TOC的敏感度远低于实验岩石物理分析结果,这主要是受实际样本量足够大和实际测井曲线的影响。由于对测井曲线进行了很好的质量控制,因此实际生产中这样的结果是可以接受的。针对测井岩石物理分析结果,如果利用最小二乘或者非线性拟合的方法对TOC进行定量估算或者分类,将无法有效地区分图 4(a)中红色、绿色及灰色样点重叠区域,即无法有效识别有效烃源岩和含油气储层。针对这种情况,这里采用概率统计的思想将岩石物理分析结果映射到地震纵、横波阻抗反演结果中,实现井-震联合反演预测TOC空间展布的目的。
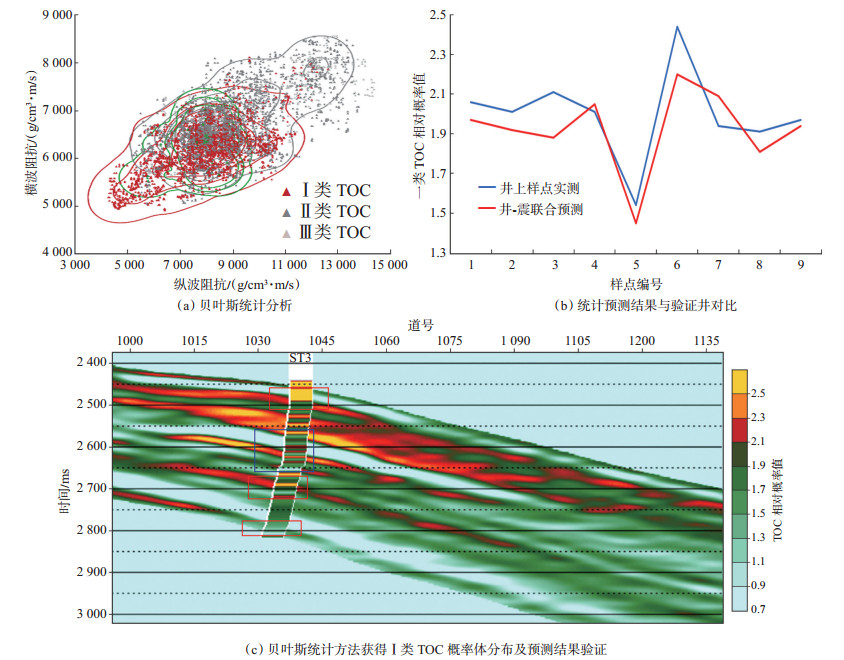
3.5 基于贝叶斯统计的TOC概率体计算研究区块目的层TOC质量分数不高于3%,富油段TOC质量分数一般高于2.2%,实验室测量显示含油气层段TOC质量分数一般大于1.8%。因此首先设定2个阈值,分别是1.8%,2.2%,将最优化估算校正后的TOC曲线按照阈值划分为3类,定义为Ⅰ,Ⅱ,Ⅲ类,分别表示含量高、中、低;然后利用测井曲线计算纵、横波阻抗;在此基础上,利用贝叶斯统计方法进行3类TOC的概率统计分析[图 5(a)]。在得到井上先验概率分布的基础上,可以将反演得到的纵、横波阻抗依据式(6)计算得到空间样点的3类TOC后验概率分布。
|
下载原图 图 5 用贝叶斯统计的TOC概率体计算及井位部署 Fig. 5 TOC probability volume calculation and well location deployment using Bayesian statistics |
为了验证该方法的适用性,针对目的层段,选取一口验证井,将实验室TOC样点观测值和对应的TOC预测值进行对比[图 5(b)],这里选取Ⅰ类TOC概率体进行对比分析。可以看到,尽管二者在数值方面存在一定的误差,但是总体分布趋势一致,并且具有较高的相关度,证明该项技术的可行性。
预测结果很好地应用于油田ST3井的井位部署。在ST3井实验室岩心TOC观测基础上,利用前述方法得到该井最优化估算TOC曲线。与钻后结果对比,井位部署时地震TOC预测结果与钻后计算TOC曲线具有很高的相关性[图 5(c)]。[图 5(c)]中色标显示值域为0~3,其为将预测Ⅰ类TOC概率体进行等比压缩以后的结果,可以直观地表征TOC值的大小,同时达到了和井上最优化估算TOC值域匹配的效果。
完钻试油结果显示4个出油层段除了第一个层段预测误差较大外,其余均与钻探结果吻合。该井在目的层段日产致密油67 m3,很好地说明了该项技术的实用性和有效性。
4 结论(1)基于构建的TOC测井评价模型,利用最优化算法可以对初始的TOC曲线进行最佳校正。基于最优化校正的TOC曲线开展敏感属性反演可以大大降低预测误差。
(2)实验室岩石物理量版可以真实地反映TOC敏感参数;基于TOC曲线的测井敏感参数分析可以证明并验证岩石物理分析结果,同时也为地震预测TOC空间分布奠定了基础。
(3)基于贝叶斯统计的TOC概率体计算,可以充分利用井上TOC和地震敏感参数的先验信息,采用概率统计的思想将岩石物理分析结果映射到地震纵、横波阻抗反演结果,实现井-震联合反演预测TOC空间展布的目的。
| [1] |
赵政璋, 杜金虎. 致密油气. 北京: 石油工业出版社, 2012: 42-47. ZHAO Z Z, DU J H. Tight oil and gas. Beijing: Petroleum Industry Press, 2012: 42-47. |
| [2] |
张厚福, 方朝亮, 高先志, 等. 石油地质学. 北京: 石油工业出版社, 1999: 86-89. ZHANG H F, FANG C L, GAO X Z, et al. Petroleum geology. Beijing: Petroleum Industry Press, 1999: 86-89. |
| [3] |
PASSEY Q R, CREANEY S, KULLAJ B, et al. A practical model for organic richness from porosity and resistivity logs. AAPG Bulletin, 1990, 74(12): 1777-1794. |
| [4] |
ZHU Y P, XU S Y. Improved rock-physics model for shale gas reservoirs. SEG Technical Program Expanded Abstracts, 2012, 1-5. |
| [5] |
胡曦, 王兴志, 李宜真, 等. 利用测井信息计算页岩有机质丰度:以川南长宁地区龙马溪组为例. 岩性油气藏, 2016, 28(5): 107-112. HU X, WANG X Z, LI Y Z, et al. Using log data to calculate the organic matter abundance in shale:a case study from Longmaxi Formation in Changning area, southern Sichuan Basin. Lithologic Reservoirs, 2016, 28(5): 107-112. |
| [6] |
郭龙, 陈践发, 苗忠英. 一种新的TOC含量拟合方法研究与应用. 天然气地球科学, 2009, 20(6): 951-956. GUO L, CHEN J F, MIAO Z Y. Study and application of a new overlay method of the TOC content. Natural Gas Geoscience, 2009, 20(6): 951-956. |
| [7] |
闫建平, 梁强, 耿斌, 等. 湖相泥页岩地球化学参数测井计算方法及应用:以沾化凹陷渤南洼陷沙三下亚段为例. 岩性油气藏, 2017, 29(4): 108-116. YAN J P, LIANG Q, GENG B, et al. Log calculation method of geochemical parameters of lacustrine shale and its application:a case of lower Es 3 in Bonan subsag, Zhanhua Sag. Lithologic Reservoirs, 2017, 29(4): 108-116. |
| [8] |
严伟, 刘帅, 冯明刚, 等. 四川盆地丁山区块页岩气储层关键参数测井评价方法. 岩性油气藏, 2019, 31(3): 95-104. YAN W, LIU S, FENG M G, et al. Well logging evaluation methods of key parameters for shale gas reservoir in Dingshan block, Sichuan Basin. Lithologic Reservoirs, 2019, 31(3): 95-104. |
| [9] |
许杰, 何治亮, 董宁, 等. 含气页岩有机碳含量地球物理预测. 石油地球物理勘探, 2013, 48(增刊1): 64-68. XU J, HE Z L, DONG N, et al. Total organic carbon content prediction of gas-bearing shale with geophysical methods. Oil Geophysics Prospecting, 2013, 48(Suppl 1): 64-68. |
| [10] |
尹正武, 陈超, 彭嫦姿. 拟声波反演技术在优质泥页岩储层预测中的应用:以焦石坝页岩气田为例. 天然气工业, 2014, 34(12): 33-37. YIN Z W, CHEN C, PENG C Z. Application of pseudo-acoustic impedance inversion to quality shale reservoir prediction:a case study of the Jiaoshiba shale gas field, Sichuan Basin. Natural Gas Industry, 2014, 34(12): 33-37. |
| [11] |
陶倩倩, 李达, 杨希冰, 等. 利用分频反演技术预测烃源岩. 石油地球物理勘探, 2015, 50(4): 706-713. TAO Q Q, LI D, YANG X B, et al. Hydrocarbon source rock prediction with frequency-divided inversion. Oil Geophysics Prospecting, 2015, 50(4): 706-713. |
| [12] |
周华建. 基于叠前OVT域偏移的河道砂体预测方法. 岩性油气藏, 2019, 31(4): 112-120. ZHOU H J. Prediction method of channel sand body based on prestack migration in OVT domain. Lithologic Reservoirs, 2019, 31(4): 112-120. |
| [13] |
石战战, 王元君, 唐湘蓉, 等. 一种基于时频域波形分类的储层预测方法. 岩性油气藏, 2018, 30(4): 98-104. SHI Z Z, WANG Y J, TANG X R, et al. Reservoir prediction based on seismic waveform classification in time-frequency domain. Lithologic Reservoirs, 2018, 30(4): 98-104. |
| [14] |
赵万金, 唐传章, 王孟华, 等. 湖相致密复杂岩性地震识别技术. 石油学报, 2015, 36(增刊1): 59-67. ZHAO W J, TANG C Z, WANG M H, et al. A seismic recognition technology of lacustrine complex tight lithology. Acta Petrolei Sinica, 2015, 36(Suppl 1): 59-67. |
| [15] |
葛瑞.马沃克, 塔潘.木克基, 杰克.德沃金.岩石物理手册: 孔隙介质中地震分析工具.徐海滨, 戴建春, 译.合肥: 中国科学技术大学出版社, 2008: 90-95. MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook: Tools for seismic analysis in porous media. XU H B, DAI J C, trans. Hefei: University of Science and Technology of China Press, 2008: 90-95. |
 2020, Vol. 32
2020, Vol. 32




