X油田特低渗透油藏井网加密效果预测方法

引用本文

张意超, 陈民锋, 屈丹, 等. X油田特低渗透油藏井网加密效果预测方法. 岩性油气藏, 2020, 32(1): 144-151, doi: 10.12108/yxyqc.20200116.

ZHANG Y C, CHEN M F, QU D, et al. Prediction method of well pattern infilling effect for ultra-low permeability reservoir in X oilfield. Lithologic Reservoirs, 2020, 32(1): 144-151, doi: 10.12108/yxyqc.20200116.

X油田特低渗透油藏井网加密效果预测方法

张意超¹, 陈民锋^1,2, 屈丹¹, 毛梅芬¹, 杨子由¹

1. 中国石油大学(北京)石油工程学院, 北京 102249;
2. 中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249

收稿日期: 2019-05-20; 修回日期: 2019-08-15; 网络首发日期: 2019-09-16

基金项目: 中海石油（中国）有限公司综合科研项目“渤海双高油田挖潜关键技术研究”（编号：YXKY-2018-TJ-04）和国家科技重大专项课题“油气资产价值评估及投资优化组合技术”子课题“油气资产价值评估体系研究”（编号：2016ZX05033005-007）联合资助

作者简介: 张意超(1996-), 男, 中国石油大学(北京)在读硕士研究生, 研究方向为油田开发系统理论方法。地址:(102249)北京市昌平区府学路18号中国石油大学。Email:18810061301@163.com.

通讯作者: 陈民锋(1971-), 男, 博士, 副教授, 主要从事油田开发和提高采收率方面的研究与教学工作。Email:cmfllp96@126.com.

摘要: 基于实际油藏井网加密调整后的动态开展效果预测研究，可为油田开发规划提供调整依据。通过对X油田特低渗透油藏井网加密调整前后开发动态变化分析，确定了加密增产效果变化规律及其主要影响因素；基于建立的反映实际油藏特点的典型数值模型，应用响应面设计方法和逐步回归方法，综合研究了不同因素变化对井网加密后增产效果的影响，并得到了反映特低渗透油藏特点的、考虑多因素影响的井网加密调整增产效果预测模型。预测模型在X油田特低渗透油藏中的实际应用表明，预测精度较高，并具有很强的针对性和实用性。本文建立的以“增产倍数”来表征油藏加密调整后的增产效果的方法，可为特低渗透油藏加密调整效果预测提供参考，并为此类油藏的开发规划提供可靠依据。

关键词: 特低渗透油藏井网加密反九点法增产效果响应面设计预测模型

Prediction method of well pattern infilling effect for ultra-low permeability reservoir in X oilfield

ZHANG Yichao¹, CHEN Minfeng^1,2, QU Dan¹, MAO Meifen¹, YANG Ziyou¹

1. College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing 102249, China;
2. State Key Laboratory of Petroleum Resources and Prospecting, China University of Petroleum(Beijing), Beijing 102249, China

Abstract: The dynamic development effect prediction research based on actual reservoir well pattern infilling adjustment can provide adjustment basis for oilfield development planning. Based on the dynamic analysis of the development before and after well pattern infilling adjustment for ultra-low permeability reservoir in X-oilfield, the change law of infilling yield-increasing effect and its main influencing factors were determined. Based on the typical numerical model established to reflect the characteristics of actual reservoir, the response surface design method and stepwise regression method were applied to comprehensively study the impact of different factors on the yield-increasing effect after well patter infilling, and the prediction model of yield-increasing effect of well pattern infilling adjustment considering multi-factors and reflecting the characteristics of ultra-low permeability reservoirs was obtained. The practical application of the prediction model for the ultra-low permeability reservoir in X oilfield shows that the prediction accuracy is high, and it has strong pertinence and practicability. The method established to characterize the yield-increasing effect of infilling adjustment can provide reference for the prediction of infilling adjustment effect of ultra-low permeability reservoirs, and provide a reliable basis for the development planning of such reservoirs.

Key words: ultra-low permeability reservoir well pattern infilling inverted nine-spot method yield-increasing effect response surface design prediction model

0 引言

井网加密调整是油田开发过程中的重要调整措施，而井网加密效果预测是油田开发规划的关键。目前，用于井网加密效果预测的方法相对较少，一般分为经验法和数值模拟法，前者方法简单，但主观性强，预测不准确，后者虽预测准确，但计算相对复杂且只适用于给定油藏条件下预测。因此，须建立一种能适合不同油藏特点且预测准确的加密效果预测模型^[1-4]。

明确不同加密条件下的开发效果，对于类似油田的加密潜力评价和油田开发规划部署，具有重要意义。X油田低—特低渗透油藏储量丰富，在开发初期多采用九点基础井网系统，并在适当的时机基于原基础井网进行整体加密调整。首先基于X油田典型油藏加密调整后的生产动态变化特征分析，确定增产效果变化规律，其次结合典型单元数值模拟和响应面设计，计算不同地质和开采条件下的油藏加密增产效果，最后针对模型计算样本，采用逐步回归方法，建立适合油田特点、考虑不同影响因素的井网加密效果预测模型，以期为特低渗透油藏的开发规划提供依据。

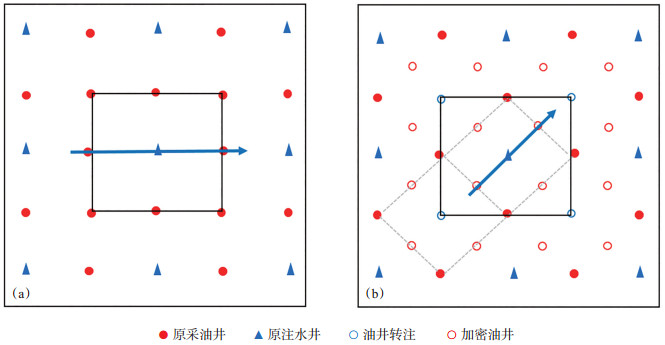
1 实际油田井网加密后的产量变化规律 1.1 井网加密形式

通过文献调研^[5-9]，结合X油田特低渗透油藏实际开发状况，根据水驱特征及剩余油分布规律研究成果，应用数值模拟技术研究加密井网形式，确定在原注水井排与采油井排之间加密2口油井，并将原井网角井转注，井网形式由300 m×300 m正方形反九点转换成小井距正方形反九点，井排方向由NE 90°转换为NE 45°。图 1为X油田初期井网形式以及井网加密调整形式。

下载原图图 1 X油田初期井网形式（a）及井网加密调整形式（b） Fig. 1 Initial well pattern of X oilfield(a)and well pattern infilling adjustment form(b)

1.2 加密后的产量变化规律

按照X油田提高采收率的总体思路，选取有代表性的典型区块，开展整体加密调整试验。本次研究选择具有代表性的X-1区块和X-2区块进行生产动态分析。

X油田基础数据如下：X-1区块油藏层间渗透率级差为8，有效厚度为15 m，原油黏度为3.12 mPa·s，渗透率为1.5 mD，井网井距为350 m×350 m；X-2区块油藏层间渗透率级差为5，有效厚度为18 m，原油黏度为2.39 mPa·s，渗透率为2.5 mD，井网井距为300 m×300 m；2个区块都采用正方形反九点井网形式，并在适当时机进行井网加密，井网调整为小井距正方形反九点。

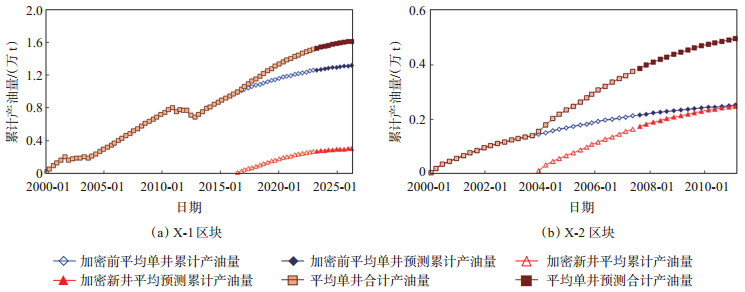
整理X-1和X-2区块的生产数据，分别得到2个区块井网加密前、后平均单井累计产油量随生产时间的变化曲线（图 2）。

下载原图图 2 井网加密前、后平均单井累计产油量随生产时间的变化曲线 Fig. 2 Curves of the average oil production per unit well before and after well pattern infilling with the production time

分析图 2得出，X-1和X-2区块在加密调整之后，老井与加密新井都具有相似的增产趋势，在这里定义增产倍数为

$ R = \frac{{{N_{\rm{L}}} + {N_3}}}{{{N_{\rm{L}}}}} $

(1)

式中：R为增产倍数；N_L为老井累计产油量，万t；N_J为加密新井累计产油量，万t。

根据实际油田生产数据，截至目前，CQ-1区块老井平均单井累计产油量为1.26万t，加密新井平均单井累计产油量为0.26万t，该区块平均单井累计产油量为1.52万t，增产倍数约为1.21；CQ-2区块老井平均单井累计产油量为0.212万t，加密新井平均单井累计产油量为0.166万t，该区块平均单井累计产油量为0.378万t，增产倍数约为1.78。采用HCZ新模型法^[10-13]，对油田实际开发数据进行2次半对数线性回归，确定预测模型的常系数a，b，从而可实现对2个区块实际累计产油量的预测。

预测油气田累计产油量的HCZ新模型为

$ \log \frac{Q}{{{N_{{\rm{P1}}}}}} = A - B\left( {t - {t_0}} \right) $

(2)

$ {N_{\rm{R}}} = {10^a} $

(3)

$ {N_{{\rm{P2}}}} = {N_{\rm{R}}}{{\rm{e}}^{ - \frac{a}{b}{e^{ - b\left( {t - {t_0}} \right)}}}} $

(4)

其中

$ A = \log a $

$ B = \frac{b}{{2.303}} $

式中：Q为油田年产油量，万t；N_P1为油田实际累计产油量，万t；N_P2为HCZ新模型预测的累计产油量，万t；N_R为油田的可采储量，万t；a，b为预测模型常系数；t₀为投产后的某初始时间，a；t为投产后的生产时间，a。

利用式（2）可计算得到常系数a，b，将其带入式（3）—（4）中，可计算油田未来的累计产油量N_P2。基于式（2）—（4）计算得到，3a之后，X-1和X-2区块增产倍数分别为1.23和1.99，相比于目前，增产倍数将分别提高1.65%和11.79%。

通过分析得出，X-1与X-2区块井网加密调整生产动态存在较大差异，其影响因素主要包括：①地质条件。在本文研究的范围内，渗透率和储层厚度越大、原油黏度越小及储层非均质性越弱，在开发和其他条件都相同时，加密调整效果越好。②开发条件。在预测地质和其他条件都相同时，则存在合理的注采井距、加密时机。地质因素和开发因素共同决定了生产动态的差异。X-2区块的地质条件优于X-1区块，且2个区块井网加密调整时机不同。

目前，一般的预测方法更多地应用于不同井网密度、井网指数条件下对井网加密后采收率的预测，而不能有效预测在不同井网形式、井网调整时机以及油藏非均质性条件下，油藏加密调整前后产量的变化。本次研究在深入分析实际油藏井网加密调整后动态变化规律的基础上，综合油藏数值模拟、数学分析方法，研究不同因素对井网加密调整效果的影响，建立不同条件下井网加密调整后产量变化预测模型。

2 增产效果预测模型的建立 2.1 预测模型建立的步骤

由于实际油田生产动态数据较少，采用一般的预测方法难以对不同油藏条件下的加密调整效果做出准确的预测，因此，本次研究将基于X油田典型区块生产动态，建立反映不同油藏条件下的数值模型，计算不同模型、不同调整时机下的产油量增产倍数。具体实现步骤为：①建立反映实际油藏特点的数值模拟模型；②确定关键参数和取值范围；③利用响应面设计计算方案；④汇总方案计算结果，初步分析增产幅度与影响因素之间的关系；⑤采用逐步回归算法，得到不同因素影响下的井网加密调整产量预测模型。

2.2 典型数值模型的建立及关键参数

利用Eclipse数值模拟软件中E100黑油模型模拟预测井网加密调整效果，x，y方向网格大小均为20m，z方向网格大小为3m。模型渗透率为1~10mD，采用反九点法井网，注采井距为300m；井网加密调整与实际油藏井网调整模式相同，采用小井距正方形反九点井网。

从典型生产动态分析得到影响增产倍数的主要因素有渗透率级差、原油黏度、井网井距、油层厚度以及井网调整时机。考虑到X油田的实际油藏特征和开发方式^[14-17]，研究了不同油藏条件下、不同井网调整时机下的加密效果。综合考虑关键参数（实际主控因素）及其取值范围分别为：渗透率级差取3~8；原油黏度取1.5~8.0mPa·s；井网井距取250~450m；有效厚度取15~30m；含水率（井网调整时机）取40%~80%。

2.3 基于响应面设计计算方案

响应面方法是利用统计学的综合实验技术解决复杂系统输入（变量）与输出（响应）之间关系的一种方法。响应面方法以试验测量、经验公式和数值分析为基础，对指定设计点集合进行连续求解，最后在设计空间中构造待测量的全局逼近^[18-19]。在本次研究中，主要是利用响应面设计筛选出能够代表所有油藏条件的样本，这样有限的样本数据就可近似代表全局样本，因此，响应面设计不仅从理论上保证了样本数据的完整性，而且大大简化了试验次数。

基于实际油藏参数的取值范围，利用响应面设计对每个因素（渗透率级差、原油黏度、有效厚度、井网井距、井网调整时机）各取3个水平，以增产倍数为最优目标，共得到46组方案（表 1）。

表 1 响应面方案设计及计算结果 Table 1 Response surface scheme design and calculation results

计算方案	响应面参数设计					计算结果
计算方案	渗透率级差	原油黏度/(mPa·s)	含水率(并网调整时机)/%	并网并距/m	有效厚度/m	预测时间/a	增产倍数
1	5.5	4.5	60	250	15.0	1~9	1.029~1.211
2	5.5	8.0	40	350	22.5	1~9	1.047~1.227
3	8	4.5	80	350	22.5	1~9	1.017~1.141
4	5.5	4.5	40	450	22.5	1~9	1.035~1.220
5	3.0	4.5	60	350	15.0	1~9	1.005~1.069
6	5.5	8.0	60	250	22.5	1~9	1.038~1.243
7	5.5	1.5	60	350	30.0	1~9	1.074~1.356
8	3.0	4.5	80	350	22.5	1~9	1.009~1.059
9	5.5	4.5	60	350	22.5	1~9	1.025~1.188
10	5.5	1.5	80	350	22.5	1~9	1.009~1.126
11	5.5	4.5	80	350	15.0	1~9	1.006~1.099
12	5.5	4.5	60	350	22.5	1~9	1.025~1.188
13	8.0	1.5	60	350	22.5	1~9	1.069~1.302
14	5.5	4.5	80	350	30.0	1~9	1.008~1.134
15	5.5	4.5	80	250	22.5	1~9	1.014~1.185
16	5.5	4.5	60	350	22.5	1~9	1.025~1.188
17	5.5	1.5	60	450	22.5	1~9	1.028~1.169
18	3.0	4.5	60	250	30.0	1~9	1.040~1.228
19	5.5	4.5	60	350	22.5	1~9	1.025~1.188
20	5.5	4.5	80	350	22.5	1~9	1.002~1.054
21	5.5	1.5	60	350	22.5	1~9	1.140~1.409
22	5.5	8.0	80	350	22.5	1~9	1.009~1.070
23	5.5	4.5	40	350	15.0	1~9	1.074~1.262
24	3.0	4.5	40	350	22.5	1~9	1.145~1.344
25	5.5	8.0	60	350	30.0	1~9	1.018~1.184
26	8.0	4.5	40	350	22.5	1~9	1.175~1.434
27	5.5	4.5	40	350	30.0	1~9	1.246~1.516
28	5.5	4.5	60	350	22.5	1~9	1.026~1.191
29	5.5	4.5	60	250	30.0	1~9	1.158~1.428
30	3.0	4.5	60	450	22.5	1~9	1.00卜1.015
31	5.5	4.5	60	450	30.0	1~9	1.002~1.112
32	5.5	4.5	60	450	15.0	1~9	1.003~1.008
33	8.0	8.0	60	350	22.5	1~9	1.007~1.150
34	5.5	8.0	60	350	15.0	1~9	1.009~1.027
35	8.0	4.5	60	450	22.5	1~9	1.002~1.105
36	3.0	4.5	60	250	22.5	1~9	1.080~1.278
37	5.5	4.5	60	350	22.5	1~9	1.026~1.191
38	5.5	1.5	60	350	15.0	1~9	1.034~1.198
39	8.0	4.5	60	350	30.0	1~9	1.078~1.315
40	8.0	4.5	60	250	22.5	1~9	1.109~1.368
41	8.0	4.5	60	350	15.0	1~9	1.003~1.158
42	3.0	8.0	60	350	22.5	1~9	1.005~1.060
43	5.5	1.5	40	350	22.5	1~9	1.262~1.531
44	3.0	1.5	60	350	22.5	1~9	1.057~1.232
45	5.5	8.0	60	450	22.5	1~9	1.003~1.006
46	5.5	4.5	40	250	22.5	1~9	1.275~1.568

下载CSV 表 1 响应面方案设计及计算结果 Table 1 Response surface scheme design and calculation results

2.4 基于逐步回归法建立预测模型

逐步回归法的基本思想是将变量逐个引入模型，每引入一个解释变量后都要进行F检验，并对已经选入的解释变量逐个进行t检验，当原先引入的解释变量由于后期解释变量的引入变得不再显著时，则将其删除，以确保每次引入新的变量之前回归方程中只包含显著性变量。这是一个反复的过程，直到既没有显著的解释变量被选入回归方程，也没有不显著的解释变量从回归方程中被剔除为止，以保证最后所得到的解释变量集是最优的^[20-22]。

2.4.1 样本数据处理

根据响应面设计，须建立相应方案下所给定油藏条件的数值模型，并根据相应方案下的油藏含水率进行井网加密，因此，共须统计92个油藏模型。油藏模型中井网形式为正方形反九点，加密形式为小井距正方形反九点，与油田实际保持一致。经过模型计算以及数据统计加密调整1 a后、3 a后、5 a后、7 a后以及9 a后的油藏平均单井累计产量增幅如表 1所列。

2.4.2 预测模型初步建立

逐步回归法选择变量的过程包含2个基本步骤：一是从回归模型中剔除经检验不显著的变量，二是引入新变量到回归模型中。常用的逐步型选元法有向前法和向后法，本次研究将采用向前法进行逐步回归，步骤如下：

（1）对p个回归自变量X₁，X₂，…，X_p分别同因变量Y建立一元回归模型，即

$ Y = {\beta _0} + {\beta _i}{X_i} + \in \;\;\;\left( {i = 1, 2, \cdots , p} \right) $

(5)

计算与变量X_i相应的回归系数的F检验统计量的值，记为F₁^（1），F₂^（1），…，F_p^（1），取其中的最大值F_i₁⁽¹⁾，即F_i₁⁽¹⁾=max{F₁⁽¹⁾, F₁⁽²⁾, …, F_p⁽¹⁾}，对给定的显著性水平α，记相应的临界值为F⁽¹⁾, F_i₁⁽¹⁾≥F⁽¹⁾，则将X_i₁引入回归模型，记I₁为选入变量指标集合。

（2）建立因变量Y与自变量子集{X_i₁, X₁}，{X_i₁, X₂}，…，{X_i₁, X_i₁-1}，{X_i₁, X_i₁+1}，{X_i₁, X_i₁+2}，…，{X_i₁, X_p}的二元回归模型，共有p-1个。计算变量的回归系数F检验的统计量值，记为($F_k^{\left( 2 \right)}\left( {k \notin {I_1}} \right)$)，选其中最大者，记为F_i₂⁽²⁾，对应自变量下角标记为i₂，即

$ F_{{i_2}}^{\left( 2 \right)} = \max \left\{ {F_1^{\left( 2 \right)}, F_2^{\left( 2 \right)} \cdots , F_{{i_1} - 1}^{\left( 2 \right)}, F_{{i_1} + 1}^{\left( 2 \right)}, F_{{i_1} + 2}^{\left( 2 \right)}, \cdots , F_p^{\left( 2 \right)}} \right\} $

(6)

对给定的显著性水平α，记相应的临界值为F⁽²⁾，F_i₂⁽²⁾≥F⁽²⁾，将变量X_i₂引入回归模型，否则，终止变量引入过程。

（3）考虑因变量对变量子集{X_i₁, X_i₂, X_k}的回归，并重复步骤（2）。依此方法重复进行，每次从未引入回归模型的自变量中选取1个，直到经检验没有变量引入为止。

将试验方案数据及统计结果的2/3数据集用于模型训练，在二次多项式回归模型的基础上，经过13步多元回归，得到增幅倍数y与诸多因素之间的二次多项式回归方程为

$ \begin{array}{*{20}{l}} {\mathit{y}{\rm{ = 1}}.{\rm{83 + 0}}.{\rm{004}}\;{\rm{4}}{x_{\rm{1}}}{\rm{ - 0}}.{\rm{06}}{x_{\rm{2}}}{\rm{ - 0}}.{\rm{024}}{x_{\rm{3}}}{\rm{ - }}}\\ {{\rm{0}}.{\rm{001}}\;{\rm{2}}{x_{\rm{4}}}{\rm{ + 0}}.{\rm{036}}{x_{\rm{5}}}{\rm{ + 0}}.{\rm{069}}{x_{\rm{6}}}{\rm{ + 0}}.{\rm{001}}\;{\rm{5}}{x_{\rm{1}}}{x_{\rm{6}}}{\rm{ - }}}\\ {{\rm{0}}.{\rm{001}}\;{\rm{4}}{x_{\rm{2}}}{x_{\rm{6}}}{\rm{ - 0}}.{\rm{000}}\;{\rm{4}}{x_{\rm{3}}}{x_{\rm{6}}}{\rm{ - 0}}.{\rm{000}}\;{\rm{07}}{x_{\rm{4}}}{x_{\rm{6}}}{\rm{ + }}}\\ {{\rm{0}}.{\rm{000}}\;{\rm{68}}{x_{\rm{5}}}{x_{\rm{6}}}{\rm{ + 0}}.{\rm{000}}\;{\rm{8}}{x_{\rm{2}}}{x_{\rm{3}}}{\rm{ + 0}}.{\rm{000}}\;{\rm{02}}{x_{\rm{3}}}{x_{\rm{4}}}{\rm{ - }}}\\ {{\rm{0}}.{\rm{0003}}{x_{\rm{3}}}{x_{\rm{5}}}{\rm{ - 0}}.{\rm{000}}\;{\rm{035}}{x_{\rm{4}}}{x_{\rm{5}}}{\rm{ + 0}}.{\rm{00013}}x_{\rm{3}}^{\rm{2}}{\rm{ - }}}\\ {{\rm{0}}.{\rm{001}}\;{\rm{4}}x_{\rm{6}}^{\rm{2}}} \end{array} $

(7)

式中：x₁为渗透率级差；x₂为原油黏度，mPa·s；x₃为井网井距，m；x₄为油层厚度，m；x₅为含水率（井网调整时机），%；x₆为井网加密后的时间，a。

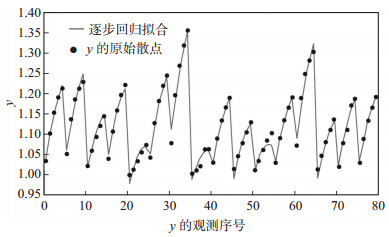
对回归方程进行显著性检验的p值（1.07×10^-47）远小于0.01，说明在显著性水平0.01下，y关于x₁，x₂，…，x₆的完全二次多项式是显著的，图 3为拟合效果。

下载原图图 3 逐步回归拟合效果 Fig. 3 Stepwise regression fitting effect

2.4.3 完善预测模型

（1）查找异常点和强影响点

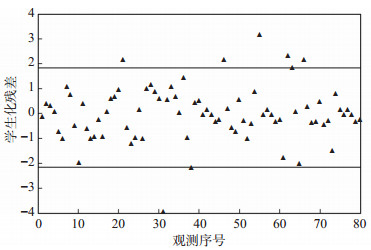
数据集中的异常点是指远离数据集中心的观测点，又称离群点；强影响点是指数据集中对回归方程参数估计结果有较大影响的观测点。通过剔除异常点和强影响点，可改进模型。本次研究将采用学生化残差值来判别异常点，并借助回归诊断图（图 4）直观地查找异常点和强影响点。

下载原图图 4 模型回归诊断图 Fig. 4 Model regression diagnosis chart

从图 4可以看出，有8组数据出现异常，它们的异常点分别是21，31，38，46，55，62，65和66。

（2）模型改进下面将检测的8组异常数据剔除后重新进行逐步回归，对模型进行改进，剔除异常点之后的完全二次多项式为

$ \begin{array}{l} \mathit{\widehat y}{\rm{ = 2}}{\rm{.069 + 0}}{\rm{.003}}{\mathit{x}_{\rm{1}}}{\rm{ - 0}}{\rm{.06}}{\mathit{x}_{\rm{2}}}{\rm{ - 0}}{\rm{.027}}{\mathit{x}_{\rm{3}}}{\rm{ - }}\\ {\rm{0}}{\rm{.0023}}{\mathit{x}_{\rm{4}}}{\rm{ + 0}}{\rm{.04}}{\mathit{x}_{\rm{5}}}{\rm{ + 0}}{\rm{.07}}{\mathit{x}_{\rm{6}}}{\rm{ + 0}}{\rm{.001}}\;{\rm{5}}{\mathit{x}_{\rm{1}}}{\mathit{x}_{\rm{6}}}{\rm{ - }}\\ {\rm{0}}{\rm{.001}}\;{\rm{5}}{\mathit{x}_{\rm{2}}}{\mathit{x}_{\rm{6}}}{\rm{ - 0}}{\rm{.000 4}}{\mathit{x}_{\rm{3}}}{\mathit{x}_{\rm{6}}}{\rm{ - 0}}{\rm{.000}}\;{\rm{07}}{\mathit{x}_{\rm{4}}}{\mathit{x}_{\rm{6}}}{\rm{ + }}\\ {\rm{0}}{\rm{.000 62}}{\mathit{x}_{\rm{5}}}{\mathit{x}_{\rm{6}}}{\rm{ + 0}}{\rm{.000 8}}{\mathit{x}_{\rm{2}}}{\mathit{x}_{\rm{3}}}{\rm{ + 0}}{\rm{.000}}\;{\rm{03}}{\mathit{x}_{\rm{3}}}{\mathit{x}_{\rm{4}}}{\rm{ - }}\\ {\rm{0}}{\rm{.000 3}}{\mathit{x}_{\rm{3}}}{\mathit{x}_{\rm{5}}}{\rm{ - 0}}{\rm{.000}}\;{\rm{035}}{\mathit{x}_{\rm{4}}}{\mathit{x}_{\rm{5}}}{\rm{ + 0}}{\rm{.000 14}}\mathit{x}_{\rm{3}}^{\rm{2}}{\rm{ + }}\\ {\rm{0}}{\rm{.000}}\;{\rm{001}}\mathit{x}_{\rm{4}}^{\rm{2}}{\rm{ - 0}}{\rm{.001 5}}\mathit{x}_{\rm{6}}^2 \end{array} $

(8)

改进后的模型（8）对回归方程进行显著性检验的$\mathit{\widehat p}$值（2.09×10^-49）小于未改进模型的p值（1.07×10^-47），说明在显著性水平0.01下，$\mathit{\widehat y}$关于x₁，x₂，…，x₆的关系更加显著。

（3）残差分析

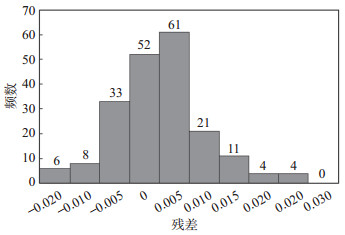
在回归诊断中，常借助残差图来验证模型的基本假定是否成立。本次研究通过绘制残差直方图（图 5）来对模型进行检验和分析。残差直方图反映了残差的分布，从图 5可以看出，该模型的残差具有明显的正态性。

下载原图图 5 模型回归诊断残差直方图 Fig. 5 Model regression diagnosis residual histogram

3 模型预测效果分析

将未参加模型运算的剩余1/3测试集代入改进后的数学模型中，经过模型计算得到预测结果，再计算产油量实际增幅与预测增幅之间的相对误差。表 2为预测模型的部分检验结果。

表 2 预测模型部分检验结果 Table 2 Partial test results of the prediction model

渗透率级差	原油黏度/(mPa·s)	含水率(井网调整时机）%	井网井距/m	油藏厚度/m	时间/a	产油量实际增幅/%	产油量预测增幅/%	相对误差/%
5.5	1.0	60	450	22.5	1	1.03	1.01	1.65
5.5	1.0	60	450	22.5	3	1.08	1.07	1.17
5.5	1.0	60	450	22.5	5	1.12	1.11	0.98
5.5	1.0	60	450	22.5	7	1.16	1.14	1.20
5.5	1.0	60	450	22.5	9	1.17	1.15	1.49
3.0	4.5	60	350	30.0	1	1.04	1.06	1.57
3.0	4.5	60	350	30.0	3	1.11	1.12	0.82
3.0	4.5	60	350	30.0	5	1.16	1.17	0.59
3.0	4.5	60	350	30.0	7	1.20	1.21	0.56
3.0	4.5	60	350	30.0	9	1.23	1.23	0.17
5.5	4.5	60	350	22.5	1	1.03	1.02	0.32
5.5	4.5	60	350	22.5	3	1.09	1.08	0.36
5.5	4.5	60	350	22.5	5	1.13	1.13	0.01
5.5	4.5	60	350	22.5	7	1.13	1.17	0.29
5.5	4.5	60	350	22.5	9	1.19	1.19	0.07
5.5	4.5	80	450	22.5	1	1.00	1.00	0.58
5.5	4.5	80	450	22.5	3	1.01	1.03	1.17
5.5	4.5	80	450	22.5	5	1.03	1.04	1.43
5.5	4.5	80	450	22.5	7	1.04	1.05	0.50
5.5	4.5	80	450	22.5	9	1.05	1.04	1.53

下载CSV 表 2 预测模型部分检验结果 Table 2 Partial test results of the prediction model

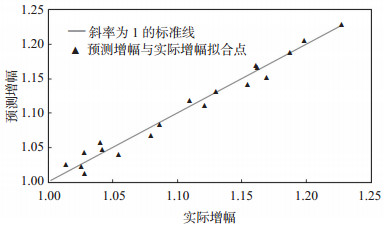
从表 2可以看出，相对误差更多集中在1%以下，最高不超过2%，说明预测值与实测值的符合率较高，应用逐步回归分析所建立的模型能较好地反映产油量增幅与渗透率级差、原油黏度等油藏参数之间的关系。图 6为对模型的拟合精度进行检验的结果，即响应面回归方程综合指标预测产油量增幅与油田实际产油量增幅的对比。从图 6可以看出，回归方程产油量预测增幅与实际增幅几乎同在倾角为45°的直线上，表明回归方程拟合精度较高。

下载原图图 6 模型预测产油量增幅与油田实际产油量增幅的关系 Fig. 6 Relationship between oil production increment predicted by model and actual oil production increment in oilfield

4 结论

（1）基于实际油藏开发动态分析，确定影响油藏加密效果的主要因素，提出用“增产倍数”来表征油藏加密调整后的增产效果。实际应用效果表明，“增产倍数”可以反映实际油藏关键动态参数的变化规律，为油藏产量规划提供可靠的依据。

（2）综合响应面设计、数值模拟方法和数学分析方法，建立了考虑受不同因素影响的“增产倍数”预测模型。该模型可以预测油藏在不同阶段、不同条件下的加密调整增产效果。

（3）X油田特低渗透油藏实际应用表明，本文建立的井网加密预测模型精度较高，并具有很强的针对性和实用性，可以为此类油藏的井网加密调整效果预测提供技术支持。

参考文献

[1]	聂光华, 高纯福. 油藏数值模拟在油田开发调整中的应用:八面河油田面4区面3块开发调整方案研究. 石油天然气学报(江汉石油学院学报), 2006, 28(4): 324-326. NIE G H, GAO C F. Application of reservoir numerical simulation in oilfield development and adjustment:Study on the development and adjustment plan of the block 4 area of the Bamianhe Oilfield. Journal of Oil and Gas Technology(Journal of Jianghan Petroleum Institute), 2006, 28(4): 324-326.
[2]	于天忠. 水平井化学驱物理模拟及数值模拟研究. 岩性油气藏, 2013, 25(5): 104-108. YU T Z. Study on physical simulation and numerical simulation of chemical flooding in horizontal wells. Lithologic Reservoirs, 2013, 25(5): 104-108. DOI:10.3969/j.issn.1673-8926.2013.05.019
[3]	张运来, 廖新武, 胡勇, 等. 海上稠油油田高含水期开发模式研究. 岩性油气藏, 2018, 30(4): 120-126. ZHANG Y L, LIAO X W, HU Y, et al. Development models for offshore heavy oil field in high water cut stage. Lithologic Reservoirs, 2018, 30(4): 120-126.
[4]	李淑霞, 盖英杰, 张俨彬. 油藏数值模拟效果的定量评价方法. 石油大学学报(自然科学版), 2001, 25(6): 58-60. LI S X, GAI Y J, ZHANG Y B. Quantitative evaluation method for numerical simulation effects of reservoirs. Journal of the University of Petroleum, China(Natural Science Edition), 2001, 25(6): 58-60.
[5]	周游, 李治平, 景成, 等. 基于"岩石物理相-流动单元"测井响应定量评价特低渗透油藏优质储层:以延长油田东部油区长6油层组为例. 岩性油气藏, 2017, 29(1): 116-123. ZHOU Y, LI Z P, JING C, et al. Quantitative evaluation of favorable reservoir in ultra-low permeable reservoir based on "petrophysical facies-flow unit" log response:a case study of Chang 6 oil reservoir set in Yanchang Oilfield. Lithologic Reservoirs, 2017, 29(1): 116-123. DOI:10.3969/j.issn.1673-8926.2017.01.015
[6]	沈瑞, 李兆国, 段宝江, 等. 王窑油田西部低渗透油藏正方形反九点井网加密调整物理模拟. 油气地质与采收率, 2014, 21(3): 89-91. SHEN R, LI Z G, DUAN B J, et al. Physical simulation of square anti-nine point well network in low permeability reservoirs in western Wangyao Oilfield. Petroleum Geology and Recovery, 2014, 21(3): 89-91. DOI:10.3969/j.issn.1009-9603.2014.03.023
[7]	向泽均, 李书静, 李新春, 等. 长庆油田加密调整提高采收率技术. 中国石油石化, 2017(3): 43-44. XIANG Z J, LI S J, LI X C, et al. Encryption adjustment and enhanced oil recovery technology in Changqing Oilfield. China Petroleum & Petrochemical Corporation, 2017(3): 43-44.
[8]	毕岐. 安塞油田王窑井网加密区水驱规律及改善开发效果研究. 西安: 西北大学, 2013. BI Q. Study on water flooding law and improvement effect of encryption area of Wangyao well in Ansai Oilfield. Xi'an: Northwest University, 2013.
[9]	常广涛. 长庆特低渗油藏典型区块水驱波及规律研究. 北京: 中国石油大学, 2017. CHANG G T. Study on the law of water flooding in typical blocks of Changqing ultra-low permeability reservoir. Beijing: China University of Petroleum, 2017.
[10]	胡建国, 陈元千. 预测油气田产量的简单模型. 中国海上油气(地质), 1995, 9(1): 53-59. HU J G, CHEN Y Q. A simple model for predicting oil and gas field production. China Offshore Oil and Gas(Geology), 1995, 9(1): 53-59.
[11]	王俊魁, 李发印. 预测油气田产量的一种新模型. 新疆石油地质, 2001, 22(1): 48-52. WANG J K, LI F Y. A new model for predicting oil and gas field production. Xinjiang Petroleum Geology, 2001, 22(1): 48-52. DOI:10.3969/j.issn.1001-3873.2001.01.013
[12]	黄全华, 付云辉, 陆云, 等. 应用改进无偏灰色模型预测油气田产量. 岩性油气藏, 2016, 28(5): 117-122. HUANG Q H, FU Y H, LU Y, et al. Application of improved unbiased grey model to predict oil and gas field production. Lithologic Reservoirs, 2016, 28(5): 117-122. DOI:10.3969/j.issn.1673-8926.2016.05.015
[13]	刘传喜, 王树平, 刘延庆. 油气田产量预测模型应用新方法. 石油与天然气地质, 2009, 30(3): 384-387. LIU C X, WANG S P, LIU Y Q. Application of new method for oil and gas field production prediction model. Oil & Gas Geology, 2009, 30(3): 384-387. DOI:10.3321/j.issn:0253-9985.2009.03.020
[14]	金拴联, 蒋远征, 杨秋莲, 等. 安塞油田注水开发技术研究. 西北地质, 2008, 41(1): 115-120. JIN S L, JIANG Y Z, YANG Q L, et al. Water injection development technology research in Ansai Oilfield. Northwest Geology, 2008, 41(1): 115-120. DOI:10.3969/j.issn.1009-6248.2008.01.014
[15]	靳星, 姬智贤, 关冲, 等. 安塞油田长6储层四性关系及有效厚度下限研究. 内蒙古石油化工, 2018(3): 109-112. JIN X, JI Z X, GUAN C, et al. Study on the four-sex relationship and the effective thickness lower limit of the Chang 6 reservoir in Ansai Oilfield. Inner Mongolia Petrochemical, 2018(3): 109-112. DOI:10.3969/j.issn.1006-7981.2018.03.039
[16]	韩星. 安塞油田H区延长组长4+5、长6油层组沉积相展布及石油聚集规律. 国外测井技术, 2019, 40(3): 50-56. HAN X. Sedimentary facies distribution and oil accumulation regularity of Chang 4+5 and Chang 6 oil-bearing formations in the Yanchang Formation of Ansai Oilfield. Foreign Well Logging Technology, 2019, 40(3): 50-56.
[17]	王磊. 长庆油田王窑南地区延安组储层研究. 大庆: 东北石油大学, 2015. WANG L. Reservoir study of Yan'an Formation in Wangyao south area, Changqing Oilfield. Daqing: Northeast Petroleum University, 2015.
[18]	罗宪波, 李金宜. 基于响应面设计方法的海上油田注聚段塞优化研究. 重庆科技学院学报(自然科学版), 2016, 18(6): 49-52. LUO X B, LI J Y. Based on the response surface design method for the optimization of the offshore oilfield segmentation stage. Journal of Chongqing University of Science and Technology (Natural Science Edition), 2016, 18(6): 49-52. DOI:10.3969/j.issn.1673-1980.2016.06.013
[19]	耿站立, 姜汉桥, 李杰, 等. 正交试验设计法在优化注聚参数研究中的应用. 西南石油大学学报, 2007, 29(5): 119-121. GENG Z L, JIANG H Q, LI J, et al. Application of orthogonal experimental design method in the study of optimization of injection parameters. Journal of Southwest Petroleum University, 2007, 29(5): 119-121. DOI:10.3863/j.issn.1674-5086.2007.05.033
[20]	游士兵, 严研. 逐步回归分析法及其应用. 统计与决策, 2017(14): 31-35. YOU S B, YAN Y. Stepwise regression analysis and its application. Statistics and Decision, 2017(14): 31-35.
[21]	付云, 尹洪超, 段林林, 等. 基于逐步回归分析的海上原油反相点预测方法研究. 广东石油化工学院学报, 2012, 22(6): 69-72. FU Y, YIN H C, DUAN L L, et al. Research on prediction method of reverse point of offshore oil based on stepwise regression analysis. Journal of Guangdong Institute of Petrochemical Technology, 2012, 22(6): 69-72. DOI:10.3969/j.issn.2095-2562.2012.06.020
[22]	顾伟欣, 周红. 基于逐步回归分析的孔隙度预测方法. 石油地质与工程, 2008, 22(1): 37-39. GU W X, ZHOU H. Porosity prediction method based on stepwise regression analysis. Petroleum Geology and Engineering, 2008, 22(1): 37-39. DOI:10.3969/j.issn.1673-8217.2008.01.012


岩性油气藏 2020, Vol. 32 Issue (1): 144-151	PDF