0 引言

近年来，川西盆地雷口坡组天然气勘探取得了重大突破，该区钻探的3口预探直井酸压后产能测试显示为（48.50~121.05）万m³/d，雷口坡组气藏有望成为继普光、元坝后又一大型海相碳酸盐岩气田^[1-3]。川西雷口坡组储层为潮坪相碳酸盐岩沉积环境，经历了多期白云化作用、溶蚀及构造作用，天然裂缝发育；纵向上多层叠置、单层厚度薄，呈薄互层状^[4-6]。雷口坡组储层属于典型的多层状裂缝型低渗透碳酸盐岩，分层酸压改造后的储层渗流特征更加复杂^[7]。

目前的碳酸盐岩储层渗流模型主要集中在天然裂缝表征^[8]、多重孔隙和多重渗透率储层渗流刻画^[9]、缝洞单元或（填充）溶洞的模拟^[10-11]等几个方面。对于复杂储层渗流特征的描述，国内外学者开展了大量的研究工作^[12-16]。在层状油气藏方面，Ehilg-Economides等^[12]分析了多层油藏系统，论证了井底压力和分层流量的组合信息能够全面地描述层状储层特征；Tariq等^[13]指出：当层状储层的层数大于2层时，渗流模型求解困难，且适用性差。在复合油气藏方面，Gomes等^[14]建立了考虑层间拟稳态窜流的N层复合模型，并总结了1960—1993年的59个层状油藏模型，其中只有5位学者考虑了储层的复合特征；曾杨等^[15]考虑油井注水后转聚合物驱替过程中流体性质的差异，采用数值有限差分的方法建立了多层窜流的复合油藏试井解释模型，但其模型认为各层的复合半径相等且未曾考虑储层裂缝特征。史文洋等^[16]归纳了1985—2018年国内学者关于低渗透裂缝型储层渗流模型的求解方法，建立了考虑储层介质变形和流体低速非达西流的裂缝性低渗透碳酸盐岩酸压改造油井动态压力响应模型，但未考虑到分层酸压改造，因此不适用于潮坪相裂缝型碳酸盐岩储层。

现存的复杂储层渗流模型不能全面地刻画川西潮坪相裂缝型碳酸盐岩分层酸压改造储层的渗流特征。为明确川西潮坪相裂缝型碳酸盐岩分层酸压储层渗流特征，厘清分层酸压改造对压力响应的影响规律，建立考虑层间窜流的裂缝型碳酸盐岩储层分层酸压改造井压力响应模型，开展分层酸压改造对压力响应影响规律的研究。实际矿场应用方面，识别雷口坡组气藏酸压气井的流动阶段，分析评价分层酸压改造程度和整体酸压的改造效果，以期为该区潮坪相裂缝型碳酸盐岩分层酸压井压力动态分析提供依据。

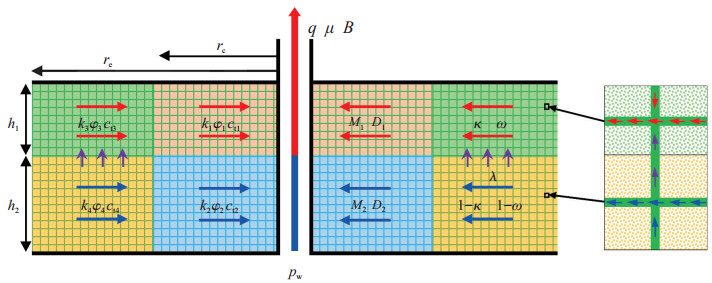
1 模型建立及求解 1.1 物理模型

潮坪相裂缝型碳酸盐岩储层基质致密，发育的天然裂缝是流体主要的渗流通道。图 1为该区潮坪相裂缝型碳酸盐岩储层中的一口分层酸压改造井物理模型，其基本假设如下：①井筒半径为r_w，井底压力为p_w，井筒储集系数为C，储层近井表皮系数为S，生产井产量为q，开井前各区压力p_j（j={1，2，3，4}）相等且为原始地层压p_i；②储层各层等厚且各向同性，顶层厚度为h₁，底层厚度为h₂，各区渗透率为k_j（j={1，2，3，4}），孔隙度为φ_j（j={1，2，3，4}），储层岩石为微可压缩介质，综合压缩系数为c_tj（j={1，2，3，4}）；③未改造区外边界为r_e，层间存在拟稳态窜流，窜流系数为λ，顶层未改造区地层系数比为κ，储容比为ω，底层未改造区地层系数比为1-κ，储容比为1-ω；④各层酸压改造范围均为r_c，改造后的层间天然裂缝沟通，不考虑改造区的层间窜流现象，顶层改造流度比为M₁，储容比为D₁，底层改造流度比为M₂，储容比为D₂；⑤储层充满单相微可压缩流体，黏度为μ，体积系数为B，裂缝系统为渗流通道，基质与裂缝系统之间无流体交换，各区流动均为达西径向渗流，忽略毛细管力、重力和温度对渗流的影响。

1.2 数学模型

定义无量纲参数如下：

（1）平均渗透率

$ {k_{\rm{a}}} = \frac{{{k_3}{h_1} + {k_4}{h_2}}}{{{h_1} + {h_2}}} $

(1)

式中：k为储层渗透率，mD；h为储层厚度，m；下标1，2，3，4表示区域1，2，3，4；下标a表示参数的平均值。

（2）平均储容系数

$ {\left( {\varphi {c_{\rm{t}}}} \right)_{\rm{a}}} = \frac{{{\varphi _3}{c_{{\rm{t}}3}}{h_1} + {\varphi _4}{c_{{\rm{t}}4}}{h_2}}}{{{h_1} + {h_2}}} $

(2)

式中：φ为储层孔隙度，%；c_t为储层综合压缩系数，MPa^-1。

（3）平均导压系数

$ {\eta _{\rm{a}}} = \frac{{{k_{\rm{a}}}}}{{\mu {{\left( {\varphi {c_{\rm{t}}}} \right)}_{\rm{a}}}}} $

(3)

式中：μ为流体黏度，mPa·s。

（4）无量纲时间

$ {t_{\rm{D}}} = \frac{{3.6{\eta _{\rm{a}}}t}}{{r_{\rm{w}}^2}} $

(4)

式中：t为生产时间，h；r_w为井筒半径，m；下标D表示参数的无量纲形式。

（5）无量纲距离

$ {r_{\rm{D}}} = \frac{r}{{{r_{\rm{w}}}}} $

(5)

式中：r为径向距离，m。

（6）无量纲压力

$ {p_{j{\rm{D}}}} = \frac{{{k_{\rm{a}}}{h_{\rm{t}}}\left( {{p_{\rm{i}}} - {p_j}} \right)}}{{1.842 \times {{10}^{ - 3}}q\mu B}} $

(6)

式中：h_t为储层总厚度，m；p_i为原始地层压力，MPa；q为生产井产量，m³/d；B为流体体积系数，m³/m³；下标j={1，2，3，4，w}，表示区域1，2，3，4，井底。

（7）无量纲井储系数

$ {C_{\rm{D}}} = \frac{{0.1592C}}{{{{\left( {\varphi {c_{\rm{t}}}} \right)}_{\rm{a}}}{h_{\rm{t}}}r_{\rm{w}}^2}} $

(7)

式中：C为井筒储集系数，m³/MPa。

（8）窜流系数

$ \lambda = \frac{{\alpha r_{\rm{w}}^2{k_4}{h_2}}}{{{k_{\rm{a}}}\left( {{h_1} + {h_2}} \right)}} $

(8)

式中：α为基质形状因子，m^-2。

（9）地层系数比

$ {\kappa _j} = \frac{{{k_j}{h_j}}}{{{k_{\rm{a}}}\left( {{h_1} + {h_2}} \right)}} $

(9)

式中：j={1，2，3，4}。

（10）储容系数比

$ {\omega _j} = \frac{{{{\left( {\varphi {c_{\rm{t}}}h} \right)}_j}}}{{{{\left( {\varphi {c_{\rm{t}}}} \right)}_{\rm{a}}}\left( {{h_1} + {h_2}} \right)}} $

(10)

式中：j={1，2，3，4}。

（11）流度比

$ {M_j} = \frac{{{k_j}}}{{{k_{j + 2}}}} $

(11)

式中：j={1，2}。

（12）扩散比

$ {D_j} = \frac{{{{\left( {\varphi {c_{\rm{t}}}h} \right)}_j}}}{{{{\left( {\varphi {c_{\rm{t}}}h} \right)}_{j + 2}}}} $

(12)

式中：j={1，2}。

潮坪相裂缝型碳酸盐岩分层酸压改造储层物理模型在拉氏空间下对应的无量纲渗流方程为

$ \left\{ \begin{array}{l} {\mathit{\boldsymbol{\kappa }}_1}\frac{\partial }{{{r_{\rm{D}}}\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{1{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right) = {\omega _1}u{{\bar p}_{1{\rm{D}}}}\\ {\mathit{\boldsymbol{\kappa }}_2}\frac{\partial }{{{r_{\rm{D}}}\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{2{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right) = {\omega _2}u{{\bar p}_{2{\rm{D}}}}\\ {\mathit{\boldsymbol{\kappa }}_3}\frac{\partial }{{{r_{\rm{D}}}\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{3{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right) + \lambda \left( {{{\bar p}_{4{\rm{D}}}} - {{\bar p}_{3{\rm{D}}}}} \right) = {\omega _3}u{{\bar p}_{3{\rm{D}}}}\\ {\mathit{\boldsymbol{\kappa }}_4}\frac{\partial }{{{r_{\rm{D}}}\partial {r_{\rm{D}}}}}\left( {{r_{\rm{D}}}\frac{{\partial {{\bar p}_{4{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right) + \lambda \left( {{{\bar p}_{4{\rm{D}}}} - {{\bar p}_{3{\rm{D}}}}} \right) = {\omega _4}u{{\bar p}_{4{\rm{D}}}} \end{array} \right. $

(13)

式中：κ1，κ2，κ3，κ4分别为区域1，2，3，4的地层系数比；r_D为无量纲距离；p_1D，p_2D，p_3D，p_4D为拉氏空间下区域1，2，3，4的无量纲压力；ω₁，ω₂，ω₃，ω₄为区域1，2，3，4的储容系数比；u为拉氏空间变量；λ为层间窜流系数。

拉氏空间下无量纲的渗流方程对应的初始条件和边界条件为

$ \left\{ \begin{array}{l} {\left. {{{\bar p}_{j{\rm{D}}}}} \right|_{{t_{\rm{D}}} \to 0}} = 0,\;\;\;\;j = \left\{ {1,2,3,4} \right\}\\ {\left. {{{\bar p}_{j{\rm{D}}}}} \right|_{{r_{\rm{D}}} = 1}} = {{\bar p}_{{\rm{wD}}}},\;\;\;\;j = \left\{ {1,2} \right\}\\ \sum\limits_{j = 1}^2 {{{\left[ {{\kappa _j}{r_{\rm{D}}}\frac{{\partial {{\bar p}_{j{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right]}_{{r_{\rm{D}}} = 1}}} = - \frac{1}{u}\\ {\left. {{{\bar p}_{j{\rm{D}}}}} \right|_{{r_{\rm{D}}} = {r_{{\rm{cD}}}}}} = {\left. {{{\bar p}_{\left( {j + 2} \right){\rm{D}}}}} \right|_{{r_{\rm{D}}} = {r_{{\rm{cD}}}}}},\;\;\;\;j = \left\{ {1,2} \right\}\\ {\left. {{M_j}\frac{{\partial {{\bar p}_{1{\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}} \right|_{{r_{\rm{D}}} = {r_{{\rm{cD}}}}}} = \frac{{\partial {p_{\left( {j + 2} \right){\rm{D}}}}}}{{\partial {r_{\rm{D}}}}}\left| {{r_{\rm{D}}} = {r_{{\rm{cD}}}},j = \left\{ {1,2} \right\}} \right.\\ {\left. {{p_{j{\rm{D}}}}} \right|_{{r_{{\rm{eD}}}} \to \infty }} = 0,\;\;\;j = \left\{ {3,4} \right\} \end{array} \right. $

(14)

式中：t_D为无量纲时间；p_wD为拉氏空间下无量纲井底压力；r_cD为内区无量纲距离；M为流度比；r_eD为无量纲边界距离。

采用拟压力函数和拟时间函数将油、气统一成相同的渗流方程^[17-19]，即

$ \left\{ {\begin{array}{*{20}{l}} {\psi = \int_0^p {\frac{{2p}}{{Z{\mu _g}}}{\rm{d}}p} }\\ {{t_{\rm{c}}} = {\mu _{{\rm{gi}}}}{c_{{\rm{gi}}}}\int_0^t {\frac{{{\rm{d}}t}}{{{\mu _{\rm{g}}}{c_{\rm{g}}}}}} } \end{array}} \right. $

(15)

式中：ψ为气体拟压力，MPa²/mPa·s；Z为气体偏差因子，m³/m³；μ_g为气体黏度，mPa·s；μ_gi为储层温度压力条件下的气体黏度，mPa·s；t_c为气体拟时间，h；c_g为气体等温压缩系数，MPa^-1；c_gi为储层温度压力条件下的气体等温压缩系数，MPa^-1。以下不再区分渗流方程中流体类型。压力和拟压力统一用压力符号p表示，时间和拟时间统一用时间符号t表示。

1.3 模型求解

各区渗流方程为Bessel方程，内区和外区渗流方程解的形式为

$ \left\{ {\begin{array}{*{20}{l}} {{{\bar p}_{j{\rm{D}}}} = {A_j}{I_0}\left( {{r_{\rm{D}}}\sqrt {{\sigma _j}} } \right) + {B_j}{K_0}\left( {{r_{\rm{D}}}\sqrt {{\sigma _j}} } \right),j = \left\{ {1,2} \right\}}\\ {{{\bar p}_{j{\rm{D}}}} = {B_j}{K_0}\left( {{r_{\rm{D}}}\sqrt \sigma } \right),j = \left\{ {3,4} \right\}} \end{array}} \right. $

(16)

式中：A，B为未知系数；${\sigma _1} = u\frac{{{\omega _1}}}{{{k_1}}}$和${\sigma _2} = u\frac{{{\omega _2}}}{{{k_2}}}$均为内区已知核函数；σ为外区未知核函数；I₀为0阶第一类修正Bessel函数；K₀为0阶第二类修正Bessel函数。对式（16）中外区渗流方程解求导，代入式（14）外区渗流方程中，得到外区渗流方程解中的未知核函数σ为一对共轭根，即

$ \left\{ {\begin{array}{*{20}{l}} {{\sigma ^ + } = \frac{{ - b + \sqrt {{b^2} - 4ac} }}{{2a}}}\\ {{\sigma ^ - } = \frac{{ - b - \sqrt {{b^2} - 4ac} }}{{2a}}} \end{array}} \right. $

(17)

式中：σ⁺，σ^-分别为未知核函数σ的2个共轭根；系数a=κ³κ⁴；系数b=-[κ₃(ω₄u+λ)+κ₄(ω₃u+λ)]；系数c=(ω₃u+λ)(ω₄u+λ)-λ²。

则外区渗流方程解表示为

$ {{\bar p}_{j{\rm{D}}}} = B_j^ + {K_0}\left( {{r_{\rm{D}}}\sqrt {{\sigma ^ + }} } \right) + B_j^ - {K_0}\left( {{r_{\rm{D}}}\sqrt {{\sigma ^ - }} } \right),j = \left\{ {3,4} \right\} $

(18)

式中：B⁺，B^-分别为未知系数B的2个共轭根。

联立外区顶层渗流方程和外区底层渗流方程得到

$ \left\{ \begin{array}{l} {X^ + } = \frac{{B_4^ + }}{{B_3^ + }} = \frac{{ - \lambda }}{{{\kappa _4}{\sigma ^ + } - {\omega _4}u - \lambda }}\\ {X^ - } = \frac{{B_4^ - }}{{B_3^ - }} = \frac{{ - \lambda }}{{{\kappa _4}{\sigma ^ - } - {\omega _4}u - \lambda }} \end{array} \right. $

(19)

式中：X⁺为未知系数B₄⁺与B₃⁺的比值；X^-为未知系数B₄^-与B₃^-的比值。

将内区和外区渗流方程的解代入初始条件及边界条件，得到关于未知系数A和B的方程组

$ \left[ {\begin{array}{*{20}{l}} {{\kappa _1}{a_{11}}}&{{\kappa _1}{a_{12}}}&{{\kappa _1}{a_{13}}}&{{\kappa _1}{a_{14}}}&0&0\\ {{a_{21}}}&{{a_{22}}}&{{a_{23}}}&{{a_{24}}}&0&0\\ {{a_{31}}}&{{a_{32}}}&0&0&{{a_{35}}}&{{a_{36}}}\\ {{M_1}{a_{41}}}&{{M_1}{a_{42}}}&0&0&{{a_{45}}}&{{a_{46}}}\\ 0&0&{{a_{53}}}&{{a_{54}}}&{{X^ + }{a_{35}}}&{{X^ + }{a_{36}}}\\ 0&0&{{M_2}{a_{63}}}&{{M_2}{a_{64}}}&{{X^ - }{a_{45}}}&{{X^ + }{a_{46}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{A_1}}\\ {{B_1}}\\ {{A_2}}\\ {{B_2}}\\ {{B_3}}\\ {B_3^ - } \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - \frac{1}{u}}\\ 0\\ 0\\ 0\\ 0\\ 0 \end{array}} \right] $

(20)

式中：${{a_{11{\rm{ = }}}}\sqrt {{\sigma _1}} {I_1}\left( {\sqrt {{\sigma _1}} } \right);}$${{a_{12}}{\rm{ = }} - \sqrt {{\sigma _1}} {K_1}\left( {\sqrt {{\sigma _1}} } \right);}$${{a_{13}} = \sqrt {{\sigma _2}} {I_0}\left( {\sqrt {{\sigma _2}} } \right);}$${{a_{14}}{\rm{ = }} - \sqrt {{\sigma _2}} {K_0}\left( {\sqrt {{\sigma _2}} } \right);}$${{a_{21}}{\rm{ = }}{I_0}\left( {\sqrt {{\sigma _1}} } \right);}$${{a_{22}} = {K_0}\left( {\sqrt {{\sigma _1}} } \right);}$${{a_{23}}{\rm{ = }} - {I_0}\left( {\sqrt {{\sigma _2}} } \right);}$${{a_{24}} = - {K_0}\left( {\sqrt {{\sigma _2}} } \right);}$${{a_{31}} = {I_0}\left( {\sqrt {{\sigma _1}} {r_{eD}}} \right);}$${{a_{32}}{\rm{ = }}{K_0}\left( {{r_{eD}}\sqrt {{\sigma _1}} } \right);}$${{a_{35}}{\rm{ = }} - {K_0}\left( {{r_{eD}}\sqrt {{\sigma ^ + }} } \right);}$${{a_{36}}{\rm{ = }} - {K_0}\left( {{r_{eD}}\sqrt {{\sigma ^ - }} } \right);}$${{a_{41}} = \sqrt {{\sigma _1}} {I_1}\left( {{r_{eD}}\sqrt {{\sigma _1}} } \right);}$${{a_{42}} = - \sqrt {{\sigma _1}} \cdot {K_1}\left( {{r_{eD}}\sqrt {{\sigma _1}} } \right);}$${{a_{45}} = \sqrt {{\sigma ^ + }} {K_1}\left( {{r_{eD}}\sqrt {{\sigma ^ + }} } \right);}$${{a_{46}} = \sqrt {{\sigma ^ - }} {K_1} \cdot \left( {{r_{eD}}\sqrt {{\sigma ^ - }} } \right);}$${{a_{53}}{\rm{ = }}{I_0}\left( {{r_{eD}}\sqrt {{\sigma _2}} } \right);}$${{a_{54}} = {K_0}\left( {{r_{eD}}\sqrt {{\sigma _2}} } \right);}$${{a_{63}}{\rm{ = }}\sqrt {{\sigma _2}} {I_1}\left( {{r_{eD}}\sqrt {{\sigma _2}} } \right);}$${{a_{64}} = - \sqrt {{\sigma _2}} {K_1}\left( {{r_{eD}}\sqrt {{\sigma _2}} } \right)}$；κ₁，κ₂分别为区域1，2的地层系数比；M₁，M₂分别为顶层、底层的流度比；X⁺，X^-分别为未知系数B₄与B₃的共轭比值；I₀为0阶第一类修正Bessel函数；K₀为0阶第二类修正Bessel函数；I₁为1阶第一类修正Bessel函数；K₁为1阶第二类修正Bessel函数；σ₁，σ₂分别为内区已知核函数；σ⁺，σ^-分别为外区未知核函数共轭根。

根据克莱姆法则解方程式（20）得到系数A_j，B_j（j={1, 2}），代入式（16）内区渗流方程解得到拉氏空间下不考虑井储和表皮效应的无量纲井底压力解。利用杜哈美叠加原理可以得到拉氏空间下考虑井储和表皮的压力解^[20]，即

$ {{\bar p}_{{\rm{wD}}}}\left( {S,{C_{\rm{D}}}} \right) = \frac{{u{{\bar p}_{{\rm{wD}}}} + S}}{{u\left[ {1 + {C_{\rm{D}}}u\left( {u{{\bar p}_{{\rm{wD}}}} + S} \right)} \right]}} $

(21)

式中：S为表皮系数；C_D为无量纲井储系数；u为拉氏空间变量；p_wD为拉氏空间下不考虑井储与表皮系数的无量纲井底压力解。

采用Stehfest数值反演方法^[21]可以得到式（21）对应实空间下的无量纲井底压力解p_wD。双对数坐标下，无量纲井底压力导数为

$ {{p'}_{{\rm{wD}}}} = \frac{{{\rm{d}}{p_{{\rm{wD}}}}}}{{{\rm{d}}\ln {t_{\rm{D}}}}} = \frac{{{\rm{d}}{p_{{\rm{wD}}}}}}{{{\rm{d}}{t_{\rm{D}}}}}{t_{\rm{D}}} $

(22)

式中：p_wD为实空间下的无量纲井底压力；t_D为实空间下的无量纲时间。

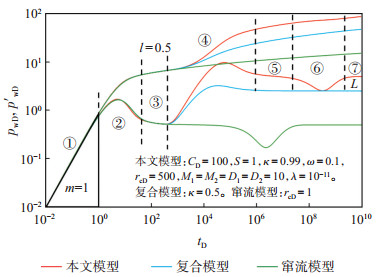
2 压力动态特征分析 2.1 模型验证

令外区各层间物性相同，层间窜流将会消失，模型退化为单层径向复合模型（图 2蓝线所示）；令复合半径等于井径，复合特征消失，模型退化为双层窜流模型（图 2绿线所示）。模型参数弱化表明，本文模型具有更广的适用性，复合模型和双层窜流模型是本文模型的特例。

2.2 典型曲线

如图 2红线所示，潮坪相裂缝型碳酸盐岩分层酸压改造后的储层存在7个流动阶段：①井筒续流阶段。由于井筒具有一定的储集能力，关井后储层流体仍向井筒续流，压力和压力导数斜率（m）均为1。②表皮过渡流阶段。该阶段的流动是由近井表皮引起的，是介于井筒续流和内区径向流之间的过渡流。③内区径向流阶段。内区储层流体径向地流入井筒，压力导数值（l）为0.5。④过渡流阶段。当压力传播到内区和外区交界面时，过渡流出现。流体在改造区的流动能力远大于未改造区，未改造区可视为储层变差的复合外区，压力和压力导数出现上升现象。⑤外区高渗层径向流阶段。压力传播到未改造区时，高渗层流体径向地流入改造区，压力导数曲线出现水平特征。⑥层间窜流阶段。压力传播到低渗层时，低渗层流体向高渗层发生层间窜流，压力导数曲线出现一个“凹子”。⑦外区总体径向流阶段。当压力传播到未改造区较远的地方时，未改造区储层流体径向地流入改造区，压力导数曲线出现水平特征（L）。

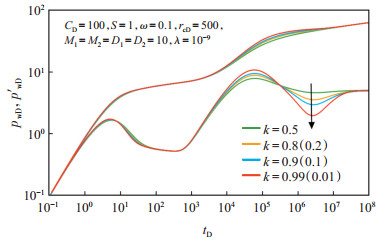
2.3 敏感性分析 2.3.1 层间物性差异

地层系数比是未改造区顶层地层系数与未改造区总地层系数的比值，表示酸压前原储层的层间物性差异程度，地层系数比越偏离0.5（0 < κ < 1），层间流动能力差异越大。当κ > 0.5表示顶层为高渗层，当κ < 0.5表示顶层为低渗层，当κ=0.5表示层间无物性差异。对于同一流体而言，地层系数比可表示为流动系数比。图 3揭示了地层系数比对层间窜流程度的影响：地层系数比等于0.5时窜流消失，压力导数曲线为水平线；地层系数比越偏离0.5，层间窜流越明显，压力导数曲线“凹子”越深。

2.3.2 改造范围

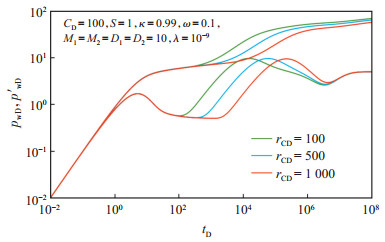
复合半径是改造区与未改造区的交界面位置，表示酸压改造范围。如图 4所示，改造范围影响过渡流出现的时间，改造范围越大过渡流越晚出现。值得注意的是：虽然改造范围只影响过渡流出现的时间，但是过渡流出现的时间不仅受改造范围的影响，还与改造程度有关（详见下文流度比、扩散比敏感性分析）。

2.3.3 分层流度比

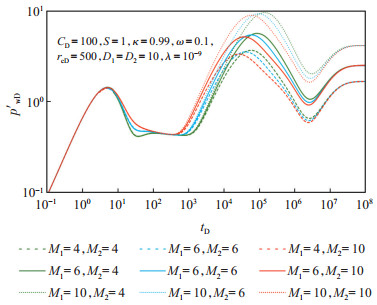
为了分析分层改造程度下的井底压力动态响应，设计了9组流度比组合（图 5）。从过渡流阶段来看：当高渗层流度比（M₁）一定时，低渗层流度比（M₂）越大，过渡流越早出现。从外区径向流阶段来看：M₁=4，L=2；M₁=6，L=3；M₁=10，L=5。也就是说，低渗层流度（M₂）比越大，过渡流越早出现；高渗层流度比（M₁）决定了外区径向流压力导数的特征：L=0.5M₁。

2.3.4 分层扩散比

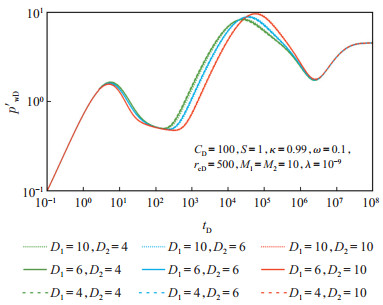
图 6为分层扩散比对压力响应的影响：当高渗层扩散比（D₁）一定时，低渗层扩散比（D₂）越大，过渡流越晚出现；当低渗层扩散比（D₂）一定时，高渗层扩散比（D₁）越大，过渡流也越晚出现，且这种差异性很小。也就是说，高渗层扩散比（D₁）对过渡流的影响可以忽略，低渗层扩散比（D₂）决定了过渡流出现的时间。

2.3.5 分层改造程度

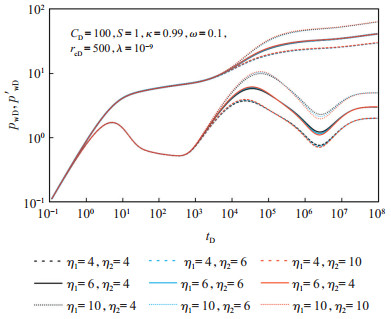
改造后储层储集流体的能力、流体的流动能力均发生了改变，储层储集能力的变化用扩散比（D）表示，流体流动能力的改变用流度比（M）表示。储层导压系数反映储层介质中压力波的传导速度，而导压系数比（η=M/D）表示改造前后压力波传导速度的比值。图 7显示了高渗层导压系数比（η₁）对压力响应的影响可以忽略，低渗层导压系数比（η₂）对压力响应的影响较大。

对比分层流度比（图 5）、分层扩散比（图 6）的分析结果可知：导压系数比能更为直观、简单地反映酸压改造对压力响应的影响，遵循流度比对压力响应的影响规律，消除流度比、扩散比对压力响应的交叉影响。因此，导压系数比综合了流度比、扩散比的影响，考虑了储层与流体改造前后的变化，更适合用来描述储层改造程度。

3 实例分析

川西雷口坡组气藏位于龙门山前构造带，被彭县断裂和关口断裂所夹持^{[5, 22-24]}，地层压力为64.26~ 66.61 MPa，温度为143.7~151.7 ℃。储层低孔低渗，天然裂缝发育^{[5, 22-24]}，测井解释孔隙度为2.9%~ 10.1 %，渗透率为0.08~6.22 mD。储层多层叠置结构明显，具有潮坪相碳酸盐岩沉积特征，属于常温、常压下的裂缝型低渗透碳酸盐岩气藏。

YS1井为雷口坡组气藏研究区块的一口预探直井，连井剖面显示YS1井具有2个沉积旋回：一是顶层以Ⅲ类储层为主的低渗层；二是底层以Ⅱ类储层为主的高渗层。YS1井射孔完井后进行酸压改造，酸压施工过程中施工曲线未显示地层破裂现象，说明酸压改造未形成高导流能力的压裂主缝。YS井未形成酸压主缝，且储层天然裂缝发育，这与物理模型的假设（4）一致。因此，认为YS1井近井改造的高渗区不存在层间窜流，而未改造区存在层间窜流。根据YS1井储层和流体参数，利用本文模型对压恢测试数据进行拟合并解释得到了储层物性参数（表 1），识别出了分层酸压改造储层的流动阶段（图 8）。

图 8显示YS1井酸压后气体流动阶段依次为：井筒续流阶段、表皮过渡流阶段、内区径向流阶段、过渡流阶段、层间窜流阶段（层间窜流由低渗的顶层流向高渗的底层）。解释参数表明：顶层流度比为6.15，扩散比为0.65，改造程度为9.46；底层流度比为15.83，扩散比为0.58，改造程度为27.29；酸压改造范围为50.30 m，分层及整体酸压程度较高。压恢历史拟合结果表明，压恢测试数据的解释结果是合理可靠的。

4 结论

（1）潮坪相裂缝型低渗透碳酸盐岩分层酸压改造储层存在7个流动阶段：①井储续流阶段；②表皮过渡流阶段；③改造区径向流阶段；④过渡流阶段；⑤未改造区高渗层径向流阶段；⑥未改造区窜流阶段；⑦总径向流阶段。

（2）改造范围、分层扩散比、分层流度比均影响过渡流。改造范围越大、低渗层扩散比越大、低渗层流度比越小，过渡流越晚出现；高渗层流度比越大，过渡流阶段压力导数上升越明显，最终压力导数值为高渗层流度比的一半；高渗层改造程度可根据未改造区径向流阶段的压力导数快速计算得到。

（3）导压系数比同时考虑了流度比和扩散比2个储层改造参数，消除了各层的流度比、扩散比对压力响应的交叉影响，遵循流度比对压力响应的影响规律，能够简单、直观地反映储层改造程度对压力响应的影响。

（4）本文模型提供了一种识别储层分层改造程度的方法，可用于评价多层裂缝型碳酸盐岩的酸压效果，确定储层分层酸压改造程度。川西雷口坡组气藏流动特征显示，酸压后储层天然裂缝沟通性良好，形成了近井高渗改造区，整体改造程度较高；压恢压力史拟合结果证明了本模型解释结果的合理性及适用性。