2. 中国石油长庆油田分公司 油气工艺研究院, 西安 710018;
3. 中国地质大学(武汉)资源学院, 武汉 430074
2. Research Institute of Oil and Gas Technology, PetroChina Changqing Oilfield Company, Xi'an 710018, China;
3. School of Earth Resources, China University of Geosciences(Wuhan), Wuhan 430074, China
非常规页岩气藏是当今世界主要的天然气资源。页岩气藏具有低孔、低渗性,体积压裂作为主要的增产措施能够改善油藏的渗流环境,增加储层的动用程度,并可大幅度提高单井产能[1]。在压裂过程中,裂缝从各个射孔簇处起裂并延伸,每条裂缝的张开都会挤压裂缝两边的地层,形成诱导应力,多条裂缝间的相互干扰则会形成更为复杂的网状裂缝[2]。对页岩储层来讲,由于天然裂缝系统和沉积层理较为发育,因而地下缝网是水力裂缝在延伸过程中遭遇天然裂缝网络发生路径延伸变化后形成的,裂缝扩展延伸不仅存在通过、偏转和终止[3]等3种模式,也可能因为压力增加而停止起裂,在遇到下一级天然裂缝处转向变得更为复杂[4-5],最终形成复杂裂缝网络。由于基质渗透率极低,裂缝网络则成为主要渗流通道,因此压后复杂裂缝系统的表征是产能模拟的核心环节[6]。
目前,将地下复杂缝网简化成平面缝、规则正交缝或分区表征均是裂缝建模的主要方法。如Xu等[7]建立了线网模型,模型中椭圆形改造区域内的2组裂缝在空间上呈三维正交分布;Chen等[8]的研究表明,地下裂缝网络的复杂性和连通性对生产过程有很大影响,这意味着双翼裂缝模型不适用于复杂裂缝网络的模拟。将裂缝网络假设为横向或正交的规则几何形态,对复杂缝网描述的信息十分有限,无法准确刻画多尺度缝网的结构特征。目前,分形理论已被广泛应用于表征致密油藏体积压裂后多孔介质的非均质性[9-11]。Wang等[12]提出了一种“分叉分形”模型来定量描述水力压裂裂缝网络的分布,实现了离散分形-裂缝网络模型(DFFN),分析了分形分叉裂缝网络中的流体流动特性,研究了分叉裂缝对复杂裂缝网络中流体流动的影响,并引入现场压裂水平井实例对流动模型的准确性进行了校准。Zhou等[13]引入分形几何系统(L-system)来描述复杂的裂缝网络,并进一步与其他模拟方法对比,发现分形裂缝网络不仅可以刻画出裂缝几何形状的分叉性,而且可以根据其分形特性来表示复杂裂缝网络的多层次特征。由此,本次研究基于随机分形几何理论,构建分形裂缝网络模型,实现裂缝网络分级、分叉特性的表征。以期为页岩气藏复杂缝网中注CO2开采模拟提供理论基础。
1 CO2注入对页岩气藏开发的影响页岩气藏基质渗透率极低,水驱开发并不可行,而页岩的总有机碳含量高,CO2和CH4在页岩有机质表面存在竞争吸附机制,使注CO2提高页岩气产量存在理论可行性。Yu等[14]采用了GEM软件开展了CO2驱替、CO2吞吐开采页岩气的数值模拟研究,结果发现CO2吞吐效果并不明显,而CO2驱替增产的原因是CO2注入维持了地层压力。Sun等[15]根据包括黏性流、克努森扩散在内的多种二元气体输运机制,建立了新双孔数学模型,并采用有限元仿真软件COMSOL研究了CO2注入对页岩气藏开发的影响,结果表明,利用CO2提高页岩气藏采收率的同时实现CO2的地质封存(CS-EGR技术),是实现页岩气藏CO2封存和提高CH4采收率的可行性方法。CO2驱油结合地质埋存技术既能有效提高原油采收率,又能实现CO2的地质封存,并可减少碳排放,是今后技术发展的重要方向[16-18]。梁凯强等[19]针对CO2驱油项目地质封存潜力评价难度大的问题,建立了一种适合延长油田低渗透油藏CO2驱油与封存的潜力评价模型。赵兴雷等[20]基于神华CO2封存项目采用的监测手段,开发了多维度CO2地质封存过程中的环境监测评估体系,采用该体系对某时典型监测数据进行评估,结果表明该封存项目属于非常安全的状态,未发现CO2泄漏风险。由此可见,常规气藏注CO2提高气体采收率的同时实现CO2埋存的技术(CO2-EGR)已经得到成功应用,而把CO2注入到非常规页岩气藏的技术(CO2-ESR)仍未成功应用到实际开发中去。
页岩气藏中的CO2埋存不仅提高了生产的经济效益,还满足了永久隔离CO2的要求,具有重大实际意义。为了更好地弄清楚CO2吞吐开采页岩气的可行性以及注入时机、注入量等参数对产量的影响,本次研究采用了Eclipse的组分模拟器模块,2020年周瑞等:随机分形体积压裂水平井CO2吞吐模拟163建立了耦合复杂分形裂缝的3 D页岩气双孔单渗模型,模拟了体积压裂情况下注CO2吞吐开采页岩气的过程。
2 页岩气藏随机分形缝网构建多数情况下,水力压裂产生的裂缝并非简单的单一双翼对称缝,而是具有复杂分叉、分支特征的网状形态[21]。由于页岩储层中的应力场具有各向异性,且存在大量天然裂缝,水力裂缝在扩展时可能不会按照传统的最小主应力方向,为满足最小能量损耗原则,裂缝的延伸扩展更具随机性,尖端可能出现许多分叉,最终在主裂缝周围产生许多次级裂缝[22]。不同尺度、不同类型的断裂裂缝均可用分形尺度模型表征,从大断裂面到微裂缝,不同尺度具有相似的分形特性,这符合分形理论基本原则[23-24]。传统的裂缝分析方法一般将裂缝等效为一个具有较高导流能力的单板裂缝,而现场实践表明,水力压裂形成并非单一裂缝,而是由主裂缝和次生裂缝结合形成的复杂网络,分叉特性与裂缝网络的连通性、复杂度息息相关,这2个特性往往是裂缝建模简化或忽略的条件,而分形几何系统中的裂缝网络具有天然的分叉特性,与天然、水力裂缝交错形成的复杂裂缝网络的分支、分叉特征相似。因此,分形几何在描述地下裂缝形态方面具有独特的优势。
L-system通过迭代函数系统(IFS),采用确定性的算法或者随机性的算法来绘制分形图[25],若L-system里面的符号服从一个以上的生成规则,且每个生成规则在每次迭代时按照一定的概率随机选取,称为随机L-system。L-system具有延伸和自我迭代的特性,由迭代特性产生的多级分支能够有效模拟和标识地下缝网的主次分级特征;随机L-system每次迭代可选择相同或不同的扩展规则,对应分形控制方程并不唯一,是多个控制方程根据不同扩展规则组合成的分形方程组,具有更高的适应度。具有多类生成组合规则的随机分形系统可保证分形裂缝形态的多样性,更能有效表征复杂裂缝网络形态。
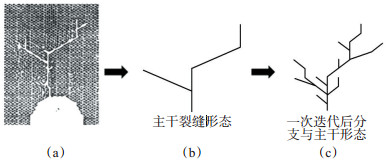
图 1中实验岩心周围的水平应力与垂直应力分别为20.8 MPa和11.3 MPa,垂向拉伸应力为27.4~41.8 MPa。观察裂缝形态抽提出其主干延伸规则[图 1(b)],将其主干形态作为生成规则代入分形几何生成系统,一次迭代后得到图 1(c)。若该裂缝为直井压裂后产生的单翼裂缝,则图 1(b)可等效为裂缝主干,而衍生后的图 1(c)则可等效为压裂后的主裂缝与次生裂缝形成的单簇裂缝或简单裂缝网络。
|
下载原图 图 1 实验裂缝切片照片[26]及其对应的分形裂缝形态 Fig. 1 Experimental fracture slice photograph and corresponding fracture fractal morphology |
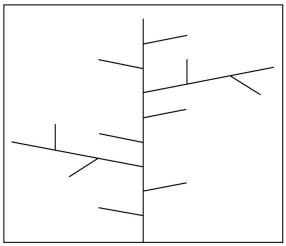
本次研究采用的是一种将L-system和随机因子结合而产生的一种随机分形模型,不涉及任何函数。根据3种基本生成规则生成裂缝,且次级裂缝生成遵循随机因子的分布。图 2是以MATLAB软件为实现平台的基于随机L-system思想的树状分形图,其生长规则为F[+F]F[-F]F[+F[+F]F[-F]F] F[+F]F[-F]F[-F[+F]F[-F]F]F[+F]F[-F]F。其中,“F”为裂缝延伸,“+”为逆时针旋转,“-”为顺指针旋转。
|
下载原图 图 2 随机分形树状图 Fig. 2 An example of random fractal tree |
分形裂缝网络作为一种分形几何系统,其形态主要受分形控制参数的影响,这些参数与几何形态的延伸和扩展相互关联,分形控制参数是研究裂缝网络特性的控制变量也是裂缝形态的拟合参数。控制分形裂缝几何形态的主要参数有4个:分形延伸长度,分形偏转角度,迭代扩展次数和预置的生成扩展规则等。分形延伸长度是控制裂缝生长扩展的主要参数,对应实际裂缝网络中的裂缝延伸长度,整体的等效裂缝半长通过压裂影响区域长度作为约束控制。分形偏转角度主要影响主裂缝产生分支分叉时改变的角度,对应岩石力学中裂缝扩展时遭遇天然裂缝的偏转角,它与整个压裂改造区的面积或体积直接相关。地下裂缝网络的连通性或裂缝的复杂程度是影响裂缝产能的主要原因之一,且裂缝级数的增加会在一定程度上影响单井产能,所以研究裂缝网络的连通性以及次生裂缝的属性和分布至关重要[27]。迭代次数是控制分形裂缝网络扩展程度以及复杂程度的主要参数,也是分形裂缝系统区别于其他裂缝网络的主要参数,每迭代一次,裂缝网络发生一次扩展和延伸,新一级裂缝会以上级裂缝为基础进行扩展、延伸和加密裂缝网络。
3 基于随机分形的页岩气藏数值模拟数值模拟模型是基于双孔介质模型建立的,双孔双渗模型不适合特低渗的页岩气藏,也就是说在基质处流体几乎是不流动的,只考虑气体扩散[28]。双孔介质模型(DP)相较于单孔介质模型(SP)可以考虑多组分的吸附模型,并可依据朗格缪等温吸附方程描述气体吸附,而且考虑到了基质部分流动的瞬态性[29]。
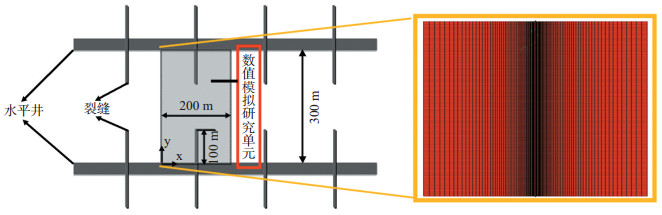
3.1 生成流程数值模拟模型包括2口平行的水平井,井距300 m,其中区域宽200 m,裂缝半长100 m(图 3)。垂直裂缝被假设为沿水平井均匀分布,同一口水平井相邻的裂缝间距约200 m,每条主裂缝半长为100 m。沿着X方向数值模拟研究单元左、右边界位于相邻主裂缝正中间处。由于裂缝分布的对称性,在不考虑流动边界条件的情况下,2条水平井即模拟区域的上下边界,由级数确定水平井的固定井底压力条件。
|
下载原图 图 3 数值模拟下的水平井区域 Fig. 3 Horizontal well area of numerical simulation |
在本次研究中,整个模型区域在X和Y方向上的长度分别为200 m和300 m,厚度为20 m,网格总数为113×145×2=32 770个。采用不规则的网格设计方法主要是为了在压力梯度大的地方,采用小尺寸网格,在其他地方,采用大尺寸网格,这样既能够得到较为精确的结果,又可以保证运行速度。基本参数详见表 1所列,在导入裂缝的参数中,裂缝开度为1.5 cm,裂缝有效渗透率为4 000 mD,模型中吸附气的解吸规律遵循Langmuir等温吸附定律。
|
|
下载CSV 表 1 页岩气藏基本参数 Table 1 Basic parameters of shale gas reservoir model |
分形裂缝导入模型的基本流程如图 4所示,具体可分解为表征复杂裂缝网络的分形几何形态生成、分形图节点坐标离散化和裂缝的属性赋值等3个部分。

|
下载原图 图 4 随机分形裂缝属性赋值流程 Fig. 4 Assignment flow chart of random fractal fracture attribute |
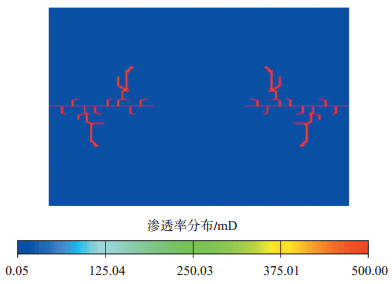
本次数值模拟通过E300模拟器CONDFRAC关键字来描述导流裂缝位置、裂缝开度(有效裂缝宽度)、裂缝渗透率、裂缝方向以及裂缝相对渗透率等参数。其中,导流裂缝位置与裂缝方向由随机分形缝网基本形态来决定,根据随机分形裂缝缝网的离散化节点坐标对数值模拟模型的网格进行等效化,本次数值模拟只考虑平面上裂缝形态产生的影响(图 5)。
|
下载原图 图 5 复杂分形裂缝模型基质及裂缝渗透率 Fig. 5 Permeability of matrix and fracture in complex fractal fracture models |
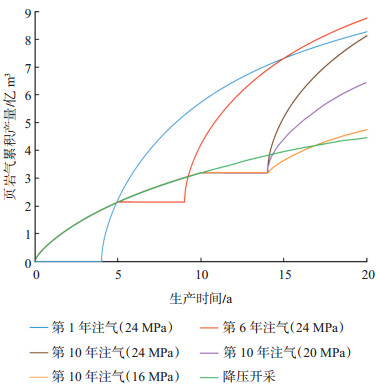
为了更好地研究CO2吞吐开采方式的可行性及CO2注入压力、注入时机、注入时间等对页岩气产量的影响,本次研究工作设计了5个对比方案。基于复杂分形裂缝页岩气藏模型进行注CO2吞吐开采页岩气的实验,采用页岩气的累积产气量及地层平均压力变化作为方案评价标准。首先,基于随机分形裂缝网络模型对比不同吞吐开采方式和衰竭开发下的页岩气产能变化规律来进行注CO2开采页岩气的可行性分析(图 6)。
|
下载原图 图 6 不同吞吐方式和衰竭开采方式下的页岩气产量 Fig. 6 Shale gas production under different modes of CO2 huff and puff and CO2 depletion |
由图 6可知,在整个生产周期内,衰竭开采方式下的累积产量并非一直最低,但最终累积产气量却最少。因为注气期间造成的产量损失导致注气开采页岩气的累积产量低于降压开采页岩气的累积产量,注气期后的1~3 a内即可成功将产量损失弥补回来,其中弥补时间主要和吞吐开采方式相关,因而页岩气的最终产量得到明显提高。综上所述,吞吐开采页岩气具有较好的效果。
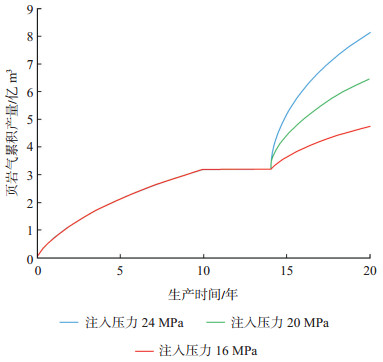
3.2.1 注入压力注入压力是影响吞吐效果的敏感参数,在定井底流压的情况下,注入压力越大,注入的CO2体积越大,气藏深部存在更多被置换出的页岩气。为研究不同注入压力对CO2埋存及页岩气产量的影响,本次研究模拟了在相同井底流压、注入时间和生产方式等条件下,以不同注气压力开发页岩气的生产过程。方案设计了3种注入压力:16 MPa,20 MPa和24 MPa等,后2种压力均小于地层的破裂压力,生产方式均为先生产10 a、注入4 a、再生产6 a,整个生产周期为20 a,页岩气累积产量如图 7所示。
|
下载原图 图 7 不同注入压力下的页岩气累积产量 Fig. 7 Cumulative production of shale gas under different injection pressures |
由图 7可看出,页岩气累积产量随着注入压力增加而提高。这是由于高的注入压力增加了地层中CO2的注入体积,有利于形成较大的CO2/CH4混合区。将CO2注入地层后进入裂缝,会由于其更强的吸附能力(3~5倍于CH4)而置换掉CH4,并将CH4从基质孔隙驱赶至裂缝。裂缝系统压力的升高会驱使CH4流向井筒,进而导致页岩气产量的增加。此外,滞留在储层的CO2以及从页岩有机质中置换出的大量页岩气可能产生增压力,进而产生较好的开采效果。降压生产时气藏压力逐渐减少,会导致生产速率变缓,而注入CO2不仅可以弥补压力损失来维持地层压力,随着越来越多的气体被生产出来,还能够将这些CO2埋存于地下。
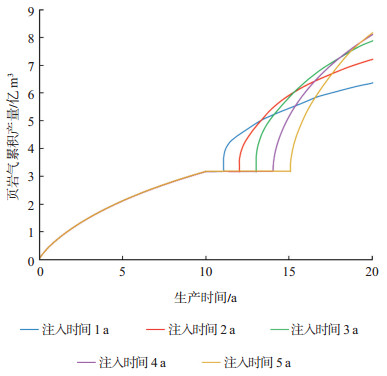
3.2.2 注入时间注入时间是影响吞吐效果的重要因素之一,注入时间直接影响注入的气体体积,进而影响到页岩气的累积产量和CO2的地质埋存。为研究不同注入时间对CO2埋存及页岩气产量的影响,本次研究模拟了在相同井底流压、注入压力、生产方式条件下,以不同注气时间开发页岩气的生产过程。实验设计了5种不同的注入时间:1 a,2 a,3 a,4 a,5 a。其中,注入压力选用24 MPa,均是生产10 a后注入。不同注入时间条件下得到的页岩气累积产量随时间的变化规律如图 8所示。
|
下载原图 图 8 不同注入时间下的页岩气累积产量 Fig. 8 Cumulative production of shale gas at different injection times |
从图 8可知,注入的CO2气体有效提高了页岩气累积产量,且页岩气最终累积产量与注入时间成正比。但注入5 a和注入4 a这2条曲线在第20 a对应的最终累积产量几乎是相同的,页岩气产量增加幅度较大的注入时间为3~4 a,若注入时长大于4 a,增加幅度将明显降低,说明注入时间并非越长越好。注气时间越长,注入地层中的气体量越大,意味着气藏深部存在更多被置换的页岩气,这将提高裂缝系统压力及页岩气浓度,进一步促使页岩气流向井筒。此外,由于注入量增加,地下缝网附近压力大幅增加,页岩气产量将大幅提升。
注入时间过长,同样无法达到理想的生产效果。随着注入时间增加,地层平均圧力增加,注气难度增加,注入气体的增加量会越来越少。同时,注入时间过长造成的产量损失需要较长生产时间去弥补,导致注气效果变差。
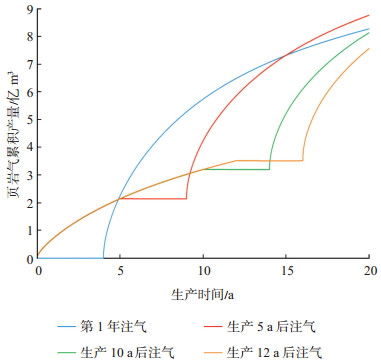
3.2.3 注入时机生产过程中随着页岩气藏压力的降低,不同的时间点注入CO2的难度也不同。注入时机会间接影响注入地下的气体总量,并进一步影响页岩气生产和CO2地质埋存。为研究不同注入时机对CO2埋存及页岩气产量的影响,本方案模拟了在相同井底流压、注入压力、注入时间等条件下,选择不同注气时间点开发页岩气的生产过程。为研究不同注入时机对CO2埋存以及页岩气产量的影响,实验设计4种不同的注入时间点:第1年(指0~1年)、第6年、第11年、第13年。此外,注入压力选用24 MPa,注气时间均为4 a。
从图 9可知,先生产5 a,再注气得到的最终累积产量最高,先注气再生产和先生产10 a再注气得到的产量相差不多,而先生产12 a再注气得到的最终累积产量最少。这说明,注入时机在注CO2提高页岩气采收率过程中存在一个最优值,注入太早或太晚的增产效果均不佳。注气过早会由于地层压力较高、注入难度较大,导致注入量减少,生产效果变差。此外,对比发现,生产5 a再注入CO2的增产效果明显好于前二者。注气过晚,气藏压力衰竭较大,相同注入期内注入气体总量虽然有所增加,但是不足以弥补生产造成的压力损耗,因此注气时间不是越晚越好。
|
下载原图 图 9 不同注气时机下的页岩气产量图 Fig. 9 Cumulative production of shale gas under different gas injection timings |
(1)在考虑页岩气的吸附-解吸特性和复杂裂缝网络模型分形特征的基础上,通过几何形态的构建、离散化和属性化,实现了随机分形网络和模型网格的等效化,建立了页岩气藏双重介质数值模型,进行了CO2吞吐开采页岩气藏的模拟研究。
(2)对比不同吞吐开采和衰竭开采方式下得到的页岩气产能发现,页岩储层中CO2更强的吸附作用使注入的CO2替换CH4,将CH4从基质孔隙驱赶至裂缝。裂缝系统的压力升高会驱使甲烷流向井筒,验证了吞吐开采的优越性。
(3)注CO2开采页岩气能提高页岩气的采收率,CO2的注入体积越大,页岩气的采收率越高,而注入量受到注气压力或注气时间的直接影响,注入压力和产量成正比。注入时间过长或者过短,无法得到预期效果,本文模拟的最佳时间是3~4 a。注入时间过短导致注气量不足,产量提升效果不明显。注气时间过长带来巨大的时间成本以及操作成本,需花更多时间弥补产量损失。
(4)注入CO2的时机也很重要,注气过早或过晚往往无法得到预期效果,应在压力降至一定范围内注气,一方面可以维持气藏压力,另一方面可以埋存大量CO2。因此,注入CO2的时机存在一个最佳值,有待进一步研究。
| [1] |
王文东, 苏玉亮, 慕立俊, 等. 致密油藏直井体积压裂储层改造体积的影响因素. 中国石油大学学报(自然科学版), 2013, 37(3): 93-97. WANG W D, SU Y L, MU L J, et al. Influencing factors of stimulated reservoir volume of vertical wells in tight oil reservoirs. Journal of China University of Petroleum(Science & Technology Edition), 2013, 37(3): 93-97. DOI:10.3969/j.issn.1673-5005.2013.03.016 |
| [2] |
DANIELS J L, WATERS G A, LE CALVEZ J H, et al. Contacting more of the Barnett Shale through an integration of real-time microseismic monitoring, petrophysics, and hydraulic fracture design. SPE 110562, 2007. |
| [3] |
GALE J F W, REED R M, HOLDER J. Natural fractures in the Barnett Shale and their importance for hydraulic fracture treatments. AAPG Bulletin, 2007, 91(4): 603-622. DOI:10.1306/11010606061 |
| [4] |
FISHER M K, WRIGHT C A, DAVIDSON B M, et al. Integrating fracture mapping technologies to improve stimulations in the Barnett shale. SPE Production & Facilities, 2005, 20(2): 85-93. |
| [5] |
HUANG J, SAFARI R, MUTLU U, et al. Natural-hydraulic fracture interaction:Microseismic observations and geomechanical predictions. Unconventional Resources Technology Conference, Denver, Colorado, 2014, 1684-1705. |
| [6] |
MAXWELL S C, STEINSBERGER N, ZINNO R. Microseismicimaging of hydraulic fracture complexity in the Barnett Shale. SPE 77440, 2002. |
| [7] |
XU W Y, WENG X W, SUN J C, et al. Wiremesh:a novel shale fracturing simulator. SPE 132218, 2010. |
| [8] |
CHEN Z M, LIAO X W, ZHAO X L, et al. A semianalytical approach for obtaining type curves of multiple-fractured horizontal wells with secondary-fracture networks. SPE Journal, 2016, 21(2): 538-549. DOI:10.2118/178913-PA |
| [9] |
陈明强, 王宁, 张阳, 等. 渭北油田浅层油藏产能预测方法. 岩性油气藏, 2017, 29(5): 134-139. CHEN M Q, WANG N, ZHANG Y, et al. Productivity prediction method of shallow reservoir in Weibei Oilfield. Lithologic Reservoirs, 2017, 29(5): 134-139. DOI:10.3969/j.issn.1673-8926.2017.05.016 |
| [10] |
ZHAO Y S, FENG Z C, LYU Z X, et al. Percolation laws of a fractal fracture-pore double medium. Fractals, 2016, 24(4): 1650053. DOI:10.1142/S0218348X16500535 |
| [11] |
WANG F Y, LIU Z C, JIAO L, et al. A fractal permeability model coupling boundary-layer effect for tight oil reservoirs. Fractals, 2017, 25(5): 1750042. DOI:10.1142/S0218348X17500426 |
| [12] |
WANG W D, SU Y L, YUAN B, et al. Numerical simulation of fluid flow through fractal-based discrete fractured network. Energies, 2018, 11(2): 286. DOI:10.3390/en11020286 |
| [13] |
ZHOU Z, SU Y, WANG W, et al. Application of the fractal geometry theory on fracture network simulation. Journal of Petroleum Exploration and Production Technology, 2017, 7(2): 487-496. DOI:10.1007/s13202-016-0268-0 |
| [14] |
YU W, AL-SHALABI E W, SEPEHRNOORI K. A sensitivity study of potential CO2 injection for enhanced gas recovery in Barnett shale reservoirs. SPE 169012, 2014. |
| [15] |
SUN H, YAO J, GAO S H, et al. Numerical study of CO2 ehanced natural gas recovery and sequestration in shale gas reservoirs. International Journal of Greenhouse Gas Control, 2013, 19: 406-419. DOI:10.1016/j.ijggc.2013.09.011 |
| [16] |
李士伦, 汤勇, 侯承希. 注CO2提高采收率技术现状及发展趋势. 油气藏评价与开发, 2019, 9(3): 1-8. LI S L, TANG Y, HOU C X. Present situation and development trend of CO2 injection enhanced oil recovery technology. Reservoir Evaluation and Development, 2019, 9(3): 1-8. DOI:10.3969/j.issn.2095-1426.2019.03.001 |
| [17] |
胡永乐, 郝明强, 陈国利, 等. 中国CO2驱油与埋存技术及实践. 石油勘探与开发, 2019, 46(4): 716-727. HU Y L, HAO M Q, CHEN G L, et al. Technologies and practice of CO2 flooding and sequestration in China. Petroleum Exploration and Development, 2019, 46(4): 716-727. |
| [18] |
陈兵, 白世星. 二氧化碳输送与封存方式利弊分析. 天然气化工(C1化学与化工), 2018, 43(2): 114-118. CHEN B, BAI S X. Analysis of the advantages and disadvantages of carbon dioxide transportation and storage. Natural Gas Chemical Industry(C1 Chemistry & Chemical Engineering), 2018, 43(2): 114-118. DOI:10.3969/j.issn.1001-9219.2018.02.023 |
| [19] |
梁凯强, 王宏, 杨红, 等. 延长油田CO2非混相驱地质封存潜力初步评价. 断块油气田, 2018, 25(1): 89-92. LIANG K Q, WANG H, YANG H, et al. Preliminary evaluation of CO2-EOR geological sequestration potential for Yanchang Oilfield. Fault-Block Oil & Gas Field, 2018, 25(1): 89-92. |
| [20] |
赵兴雷, 崔倩, 王保登, 等. CO2地质封存项目环境监测评估体系初步研究. 环境工程, 2018, 36(2): 15-20. ZHAO X L, CUI Q, WANG B D, et al. Preliminary study on environmental monitoring assessment system for CO2 storage projects. Environmental Engineering, 2018, 36(2): 15-20. |
| [21] |
STALGOROVA K, MATTAR L. Analytical model for unconventional multifractured composite systems. SPE Reservoir Evaluation & Engineering, 2013, 16(3): 246-256. |
| [22] |
TALEGHANI D A, OLSON J E. How natural fractures could affect hydraulic-fracture geometry. SPE Journal, 2013, 19(1): 161-171. DOI:10.2118/167608-PA |
| [23] |
徐光黎. 岩石结构面几何特征的分形与分维. 水文地质工程地质, 1993, 20(2): 20-22. XU G L. Fractal and fractal dimension of geometric features of rock structural planes. Hydrogeology and Engineering Geology, 1993, 20(2): 20-22. |
| [24] |
LA POINTE P R. A method to characterize fracture density and connectivity through fractal geometry. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1988, 25(6): 421-429. |
| [25] |
丁永胜, 堵秀凤, 张水胜. Matlab分形植物模拟. 齐齐哈尔大学学报(自然科学版), 2008, 24(3): 63-66. DING Y S, DU X F, ZHANG S S. fractal plant simulation based on Matlab. Journal of Qiqihar University(Natural Science Edition), 2008, 24(3): 63-66. DOI:10.3969/j.issn.1007-984X.2008.03.027 |
| [26] |
HUANG J I, KIM K. Fracture process zone development during hydraulic fracturing. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1993, 30(7): 1295-1298. |
| [27] |
JONES J R, VOLZ R, DJASMARI W. Fracture complexity impacts on pressure transient responses from horizontal wells completed with multiple hydraulic fracture stages. SPE 167120, 2013. |
| [28] |
VINCENT M C. Optimizing transverse fractures in liquid-rich formations. SPE 146376, 2011. |
| [29] |
GONG B, QIN G, TOWLER B F, et al. Discrete modeling of natural and hydraulic fractures in shale-gas reservoirs. SPE 146842, 2011. |
 2020, Vol. 32
2020, Vol. 32



