油井的初期产能预测是油田开发的重要环节,可为油藏的开发动态分析和调整提供依据,也常用于对新钻井的经济效益进行评估。关于产能预测模型,①根据油藏流体的渗流机理建立数学模型[1-5],其渗流微分方程组建立过程较为复杂,求解时需要多种假设条件,适用条件严格。②利用地质资料,建立地质模型,使用已有的开发资料进行历史拟合,然后用油藏数值模拟的方法预测目标井位的产能[6],但是地质模型和数值模型的建立需要较高的时间成本和计算成本[7]。另外现场上也常采用经验和类比的方法,其误差较大。
在油田开发过程中,积累了大量关于油藏的地质数据、生产数据和工程数据等,这些数据对于深度认识油藏具有极其重要的作用,机器学习算法可以帮助人们从这些已有的数据中挖掘出需要的信息。潘有军等[8]使用多元线性回归方法建立了火山岩压裂水平井的产能模型,但多因素对产能的影响规律,线性模型的表征仍不够完善。田冷等[9]使用改进的BP神经网络建立了长庆气田的产能预测模型,该模型只有较大的样本容量才能建立一个高精度的神经网络模型,而且容易产生过拟合现象。支持向量机(SVM)是以统计学习理论为基础的新的机器学习算法,其建模过程简单,耗时较少,能够很好地解决小样本、高维数的问题,而且可以表征多个特征与目标之间的非线性关系,预测结果也更加准确。王威[10]使用支持向量机方法对致密油藏的产能进行了研究,赵传峰等[11]使用支持向量机方法,采用不同的核函数对调剖后的增油量进行了预测,发现其精度比BP神经网络预测精度高出很多。张志英等[12]在油藏数值模拟的基础上,基于支持向量机形成了水平井的产能预测方法。
支持向量机的关键参数,惩罚因子、松弛因子等对模型的精确度、稳定性及泛化性能有较大的影响,这些参数的优化对能否形成一个高性能的模型型至关重要。目前用于支持向量回归机参数选择的方法主要有3种:①利用经验对参数进行选择,这对使用者和样本有较大的依赖性;②网格搜索寻优,它的不足之处在于步长的选择,步长小,计算量大、时间长,步长大,容易错失全局最优解;③利用优化算法对参数进行优选。灰狼算法具有良好的自组织学习性,而且参数简单、全局搜索能力强、收敛速度快、易于实现。因此,采用灰狼算法对支持向量机进行优化[13],以特低渗油藏为例,建立油井的产能预测模型,以期提高产能预测的效率和精度。
1 特征因素选取影响油藏初期产能的因素首先是地质因素,包括孔隙度、渗透率、含油饱和度、油层有效厚度和射孔段有效厚度等。其次是工程因素。对于特低渗透油藏来说,必须通过压裂产生高渗条带,形成基质孔隙与井筒的流动通道,从而建立产能,这里选用压裂加砂量、加砂强度和泵效来分析工程因素对初产的影响。最后是开发因素,包括能量保持状况以及井网井距等因素,能量的保持状况用动液面的高度来表征,动液面越高,地层能量保持越好,动液面越低,地层能量保持程度越低;井网井距用油井的初始饱和度来表示,初始含水饱和度越高,表示注采井网的井距越小,初始含水饱和度越低,表示注采井网的井距越大。基于某特低渗油田34口生产井,选取上面提到的10个特征参数作为分析产能的影响因素,建立产能预测模型的基础数据,如表 1所列。
|
|
下载CSV 表 1 某特低渗油藏单井产能影响因素及对应初产[14] Table 1 Initial productivity and influencing factors of an ultra-low permeability reservoir |
首先利用皮尔逊相关性分析各个因素之间的相关关系。皮尔逊相关关系是用来量度2个变量之间的线性相关性。相关系数从-1(负相关)到1(正相关)之间变化,相关系数为0时意味着这2个变量之间没有相关关系。计算方法[15]为
| $ {\rho _{X, Y}} = \frac{{{\mathop{\rm cov}} (X, Y)}}{{\sigma X\sigma Y}} $ | (1) |
式中:ρX, Y为参数X和参数Y之间的相关系数,cov为协方差,σ是标准差。
利用皮尔逊相关关系,计算了各参数之间,以及各参数与初产之间的相关系数,结果如图 1所示。可以看出,在特低渗油藏中,渗透率和孔隙度有较强的线性相关关系,孔隙度越大,渗透率越大。油层有效厚度、射孔段厚度以及压裂加砂量有一定相关性,油层厚度越大,射孔段厚度越大,相应的压裂加砂量也越大。另外,根据各个因素与初产的相关系数可以看出,射孔段厚度,压裂加砂量以及油层的有效厚度与初产的相关性较强。
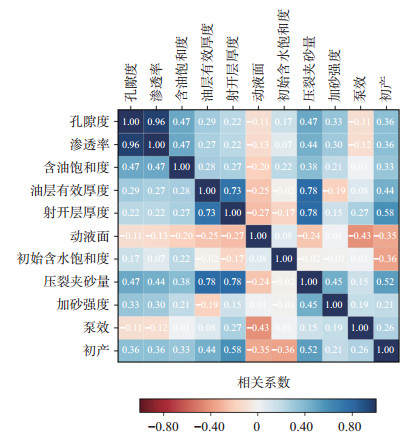
|
下载原图 图 1 初期产能影响因素相关关系矩阵 Fig. 1 Correlation matrix of influencing factors of initial productivity |
皮尔逊相关系数只能简单分析单因素对产能的线性影响关系,在油藏开发过程中,产能是在多个因素共同作用下的非线性结果。为了明确各个地质参数、工程参数和开发参数对初期产能的非线性影响程度,使用随机森林方法确定初期产能的主控因素。随机森林是一种集成机器学习方法,利用随机采样技术和节点随机分裂技术构造多棵决策树,通过投票得到最终结果,其用于特征排序时主要有2种方法,一种是对每个特征按照Gini不纯度进行排序,另一种是测量每种特征对模型准确率的影响,这里使用后一种方法[16]。
随机森林建模时随机采样未被抽到的数据称为袋外数据集,这些数据没有参与训练集模型的拟合,可以用来检验模型的泛化能力。在对模型进行重要性排序时,使用相应的袋外数据计算它的袋外误差r1,然后袋外数据中的某个特征的顺序被随机变换,再次计算袋外误差r2,假设随机森林有N棵树,那么某个特征的重要性I为
| $ I = \frac{{\sum\limits_{i = 1}^N {\left( {{r_1} - {r_2}} \right)} }}{N} $ | (2) |
根据上述原理,计算得到该特低渗油藏每个特征对初产的重要性如表 2所列。
|
|
下载CSV 表 2 产能影响因素重要性排序 Table 2 Importance order of influencing factors of productivity by Random Forest |
利用随机森林方法对产能影响因素重要性的排序结果表明,特低渗透油藏初期产能的5个主控因素为压裂加砂量、射孔段厚度、初始含水饱和度、油层有效厚度以及加砂强度,其重要性指标I均大于0.20。因此,在开发特低渗透油藏时,新井井位应选在油层有效厚度大的区域,完井时增大射孔段厚度,压裂施工时增大加砂量,提高加砂强度,从而提高初期产能。另外,开发因素中油井初始含水饱和度对初产的影响因素较大,其表征的是井网井距的影响。因此,在特低渗透油藏开发中,合理的井网井距对产能的提高和保持也有着重要的作用。
3 模型的建立 3.1 支持向量机(SVM)原理根据文献[7]报道,支持向量机算法最初是Vladimie等提出的,它是一种用来分析数据和模式识别的有监督学习方法,可以对数据进行分类和回归分析。这里所用到的是支持向量回归机,其原理如图 2所示,旨在寻找一个最优的超平面,使得所有样本离该最优超平面的距离最小。
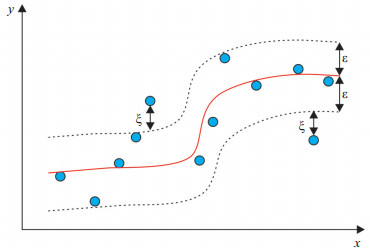
|
下载原图 图 2 支持向量机原理示意图 Fig. 2 Schematic diagram of support vector machine |
超平面可用式(3)表示,最优的回归超平面为所对应的凸二次规划问题,如(式4)所示[18]:
| $ f(x) = {w^T} \cdot x + b $ | (3) |
| $ \min \frac{1}{2}{\left\| w \right\|^2} + c\sum\limits_{i = 1}^l {\left( {{\xi _i} + \xi _i^*} \right)} $ | (4) |
| $ \mathit{s}{\rm{.}}\mathit{t}{\rm{. }}\left\{ {\begin{array}{*{20}{l}} {{y_i} - w\mathit{\Phi }\left( {{x_i}} \right) - {\rm{b}} \le \varepsilon + {\xi _i}}\\ { - {y_i} + w\mathit{\Phi }\left( {{x_i}} \right) + {\rm{b}} \le \varepsilon + \xi _i^*, i = 1, 2, \ldots , l}\\ {{\xi _i} \ge 0, \xi _i^* \ge 0} \end{array}} \right. $ |
式中:c为惩罚参数,其取值反映了对式中2个部分重要性的权衡;ξi和ξi*为松弛变量,以降低对超平面的要求;ε为不敏感参数,定义了不敏感带的宽度;Φ(x_i)为映射函数。
为了使式(4)容易求解,使用拉格朗日函数将目标函数转化为其对偶形式:
| $ \begin{array}{*{20}{c}} {\mathop {\max }\limits_{_{\alpha , {a^*}}} \left[ { - \frac{1}{2}\sum\limits_{i = 1}^l {\sum\limits_{j = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} } \left( {{\alpha _j} - \alpha _j^*} \right)K\left( {{x_i}, {x_j}} \right) - } \right.}\\ {\left. {\sum\limits_{i = 1}^l {\left( {{\alpha _i} + \alpha _i^*} \right)} \varepsilon + \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} {y_i}} \right]} \end{array} $ | (5) |
| $ {\bf{s}}{\bf{.t}}{\bf{.}}{\rm{ }}\left\{ {\begin{array}{*{20}{l}} {\sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} = 0}\\ {0 \le {\alpha _i} \le {\rm{c}}}\\ {0 \le \alpha _i^* \le {\rm{c}}} \end{array}} \right. $ |
式中:αi和αi*为拉格朗日乘子向量;K (xi, xj)为核函数,可以将高维空间的内积运算转换为低维空间的核函数运算。利用分块算法、Osuna、序列最小优化算法、或者增量学习法求得αi后,最优超平面回归函数可由式(6)确定
| $ \begin{array}{l} f(x) = {w^*} \cdot \mathit{\Phi }(x) + {b^*} = \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} \mathit{\Phi }\left( {{x_i}} \right)\mathit{\Phi }(x) + {b^*}\\ \;\;\;\;\;\;\;\; = \sum\limits_{i = 1}^l {\left( {{\alpha _i} - \alpha _i^*} \right)} K\left( {{x_i}, x} \right) + {b^*} \end{array} $ | (6) |
灰狼优化算法是通过模拟狼群的等级制度和捕食策略,以迭代的方式不断寻找最优值的一种群优化算法[19]。狼的生活习性以群居为主,每个群体中有7~12只狼,具有较为严格的等级制度,如图 3所示。
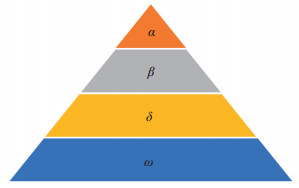
|
下载原图 图 3 狼群等级层次机制 Fig. 3 Hierarchy mechanism of grey wolf |
α是狼群中管理能力最强的,被奉为头狼,因此所有狼都听从它的指挥,其主要负责决策狼群的捕猎、驻地和休息时间等。β是α的顾问,帮助α制定决策及安排其他活动,也是狼群中秩序的维持者。当α去世或者年龄增大,β也是最好的α候选人。排在第3层的是δ狼,听从α和β的指示,并指挥ω,它们主要负责侦查、放哨、捕猎、看护等事务。年老的α和β也都会降级为δ。ω等级最低,必须服从其他等级狼的指挥和调度,也负责照顾幼狼,其数量可以平衡种群的内部关系。捕食活动由α带领,首先狼群以团队形式对猎物进行跟踪、追赶、靠近,然后从各个方向包围并恐吓猎物直到猎物停止运动,最后攻击猎物。
3.2.2 数学模型捕食过程中,狼群与猎物的距离D可用式(7)表示,狼群根据猎物位置和与猎物的距离更新其位置,用式(8)表示[20]:
| $ D = \left| {C \cdot {X_p}(t) - X(t)} \right| $ | (7) |
| $ X(t + 1) = {X_p}(t) - A \cdot D $ | (8) |
式中:X为狼的位置向量;Xp为猎物的位置向量;t为当前迭代步;A和C均为系数向量,通过调整这2个向量,狼可以到达猎物周围的不同位置,其计算方法可用式(9)—(10)表示:
| $ A=2 a r_{1}-a $ | (9) |
| $ C = 2 \cdot {r_2} $ | (10) |
式中:a在迭代过程中,从2到0线性减小;r1和r2为[0, 1]之间的随机向量。
假定α,β和δ对猎物的潜在逃窜位置有较好的洞察能力,整个捕食过程由α,β和δ主导,而且α狼的位置是最优的,其次是β,最后是δ。首先根据式(11)确定α,β和δ到猎物的距离,再根据式(12)移动到下一步的位置,ω则根据这3头位置最好的狼来更新自己的位置。根据上述方法,不断迭代,直到满足终止条件,便可得到优化目标的最优解、次优解等。
| $ {D_\alpha } = \left| {{C_1} \cdot {X_\alpha } - X} \right|, {D_\beta } = \left| {{C_2} \cdot {X_\beta } - X} \right|, {D_\delta } = \left| {{C_3} \cdot {X_\delta } - X} \right| $ | (11) |
| $ {X_1} = {X_\alpha } - {D_\alpha }{A_1}, {X_2} = {X_\beta } - {D_\beta }{A_2}, {X_3} = {X_\delta } - {D_\delta }{A_3} $ | (12) |
| $ X(t + 1) = \frac{{{X_1} + {X_2} + {X_3}}}{3} $ | (13) |
初期产能预测模型建立流程如图 4所示,首先将收集到的数据进行归一化处理,将其中80%作为训练集,20%作为测试集,然后使用训练集建立基于支持向量机的产能预测模型。整个过程使用MATLAB2016 b编程实现,支持向量机调用LIBSVM工具箱进行设计,选取径向基函数作为核函数,决定支持向量机性能的2个关键参数,惩罚参数c和核函数参数g使用上述灰狼算进行优化,直至满足迭代终止条件。最后使用测试集对模型的准确性进行评估。
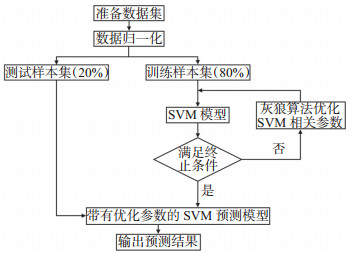
|
下载原图 图 4 GWO-SVM产能预测模型建模流程 Fig. 4 Workflow of GWO-SVM prediction model |
利用统计的某特低渗油藏34口生产井的初期产量以及影响初期产量的10种因素作为样本库,其中27口井数据作为训练集,7口井作为测试集,使用网格搜索寻优的支持向量机(GRID-SVM)和灰狼算法优化的支持向量机(GWO-SVM)建立初期产能的预测模型,其中灰狼算法优化得到的支持向量机参数分别为c = 52.40,g = 0.01。
多元线性回归模型[14],网格寻优的支持向量机模型(GRID-SVM)和灰狼算法优化的支持向量机模型(GWO-SVM)的预测结果如表 3所示,从表中可以看出,灰狼算法优化的支持向量机建立的产能预测模型比多元线性回归预测结果和网格寻优的支持向量机预测结果误差小得多,且均在12%以下。多元线性回归和网格寻优的支持向量机对油井初期产能预测结果的误差较大,对P43-841井预测结果的相对误差甚至超过了40%。3种方法的产能预测结果对比如图 5所示,可以清楚地看到,灰狼算法优化的支持向量机产能模型预测结果更准确。
|
|
下载CSV 表 3 不同方法单井初期产能预测结果 Table 3 Prediction results of different forecast models |
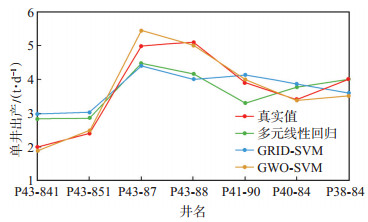
|
下载原图 图 5 不同方法单井初期产能预测结果 Fig. 5 Prediction results of initial productivity by different forecast model |
另外,在编程计算过程中发现,GWO-SVM比GRID-SVM更加高效。当GRID-SVM扩大网格搜索范围或减小搜索步长时,计算所需要的时间会超过几个小时。相反,GWO-SVM往往在几十秒之内便能得到结果,而且精度较高。
5 结论(1)油藏初期产能的影响因素包括地质、工程、开发方面的10种因素。皮尔逊相关性分析表明:射孔段厚度、压裂加砂量和油层有效厚度均与初期产能有较强的线性相关性。
(2)用随机森林方法表征特低渗油藏初期产能影响因素与初产之间的非线性关系,确定的初产主控因素为压裂加砂量、射孔段厚度、初始含水饱和度、油层有效厚度和加砂强度。
(3)基于灰狼算法优化的支持向量机产能预测模型,对测试集7口井的预测结果误差均小于12%,平均预测结果误差为5%,比多元线性回归和网格搜索优化的支持向量机预测结果准确度提高10%以上。该模型也可以推广到其他类型的油气藏初期产能预测。
| [1] |
刘海龙, 刘传喜, 孙建芳, 等. 致密砂岩油藏部分射开压裂直井产能分析. 辽宁石油化工大学学报, 2018, 38(1): 37-43. LIU H L, LIU C X, SUN J F, et al. The productivity analysis of vertical well with partial penetration fracture in tight sandstone reservoir. Journal of Liaoning Shihua University, 2018, 38(1): 37-43. DOI:10.3969/j.issn.1672-6952.2018.01.007 |
| [2] |
陈明强, 蒲春生, 赵继勇, 等. 变形介质低渗透油藏油井真实产能计算与分析. 西安石油大学学报(自然科学版), 2006, 21(2): 18-22. CHEN M Q, PU C S, ZHAO J Y, et al. Calculation and analysis of the true productivity of a well of low permeable reservoirs of a deformation medium. Journal of Xi'an Shiyou University(Natural Science Edition), 2006, 21(2): 18-22. DOI:10.3969/j.issn.1673-064X.2006.02.005 |
| [3] |
任俊杰, 郭平, 汪周华, 等. 非线性渗流条件的低渗油藏产能计算方法. 西安石油大学学报(自然科学版), 2013, 28(1): 57-60. REN J J, GUO P, WANG Z H, et al. A new method for productivity evaluation of low permeability reservoirs with nonlinear seepage characteristics. Journal of Xi'an Shiyou University (Natural Science Edition), 2013, 28(1): 57-60. DOI:10.3969/j.issn.1673-064X.2013.01.010 |
| [4] |
姬靖皓, 席家辉, 曾凤凰, 等. 致密油藏分段多簇压裂水平井非稳态产能模型. 岩性油气藏, 2019, 31(4): 157-164. JI J H, XI J H, ZENG F H, et al. Unsteady productivity model of segmented multi-cluster fractured horizontal wells in tight oil reservoir. Lithologic Reservoirs, 2019, 31(4): 157-164. |
| [5] |
李小龙, 许华儒, 刘晓强, 等. 径向井压裂裂缝形态及热采产能研究. 岩性油气藏, 2017, 29(6): 154-160. LI X L, XU H R, LIU X Q, et al. Fracture morphology and production performance of radial well fracturing. Lithologic Reservoirs, 2017, 29(6): 154-160. DOI:10.3969/j.issn.1673-8926.2017.06.020 |
| [6] |
安永生.复杂井产能动态预测数值模拟研究.北京: 中国石油大学(北京), 2008. AN Y S. Numerical simulation study on dynamic prediction of complex well productivity. Beijing: China University of Petroleum(Beijing), 2008. |
| [7] |
CAO Q, BANERJEE R, GUPTA S, et al. Data driven production forecasting using machine learning. SPE180984, 2016.
|
| [8] |
潘有军, 荆文波, 徐赢, 等. 火山岩油藏水平井体积压裂产能预测研究. 岩性油气藏, 2018, 30(3): 159-164. PAN Y J, JING W B, XU Y, et al. Productivity prediction of horizontal wells by volume fracturing in volcanic reservoirs. Lithologic Reservoirs, 2018, 30(3): 159-164. |
| [9] |
田冷, 何顺利, 顾岱鸿, 等. 改进BP神经网络模型在长庆气田产能预测中的应用. 石油天然气学报, 2008, 30(5): 106-109. TIAN L, HE S L, GU D H, et al. Application of neural network technique for productivity evaluation in Changqing gas field. Journal of Oil and Gas Technology, 2008, 30(5): 106-109. DOI:10.3969/j.issn.1000-9752.2008.05.025 |
| [10] |
王威. 致密油藏水平井体积压裂初期产能预测. 新疆石油地质, 2016, 37(5): 575-579. WANG W. Forecast of initial horizontal well productivity in tight reservoirs by volumetric fracturing process. Xinjiang Petroleum Geology, 2016, 37(5): 575-579. |
| [11] |
赵传峰, 姜汉桥, 郭新华. 支持向量机在小样本预测中的应用. 油气地面工程, 2009, 28(2): 21-23. ZHAO C F, JIANG H Q, GUO X H. Application of support vector machine in small sample prediction. Oil and gas ground engineering, 2009, 28(2): 21-23. |
| [12] |
张志英, 姜汉桥, 郭虎, 等. 基于支持向量机的水平井产能预测方法. 大庆石油地质与开发, 2010, 29(1): 78-80. ZHANG Z Y, JIANG H Q, GUO H, et al. Horizontal well productivity prediction based on SVM. Petroleum Geology and Oilfield Development in Daqing, 2010, 29(1): 78-80. DOI:10.3969/J.ISSN.1000-3754.2010.01.018 |
| [13] |
BIAN X Q, HUANG J H, WANG Y, et al. Prediction of wax disappearance temperature by intelligent models. Energy & Fuels, 2019, 33(4): 2934-2949. |
| [14] |
王建. 多元回归法在特低渗透油藏初期产量预测中的应用:以坪北油田为例. 江汉石油科技, 2017(4): 32-39. WANG J. Application of multiple regression method in early production prediction of ultra-low permeability reservoir. Jianghan Petroleum Technology, 2017(4): 32-39. |
| [15] |
翁永春, 祝一帆, 孟浪, 等. 基于多历史覆冰过程的输电线路覆冰增长预测. 三峡大学学报(自然科学版), 2019, 41(1): 75-79. WENG Y C, ZHU Y F, MENG L, et al. Prediction of icing growth of transmission line based on multi-history icing process. Journal of China Three Gorges University(Natural Science Edition), 2019, 41(1): 75-79. |
| [16] |
姚登举, 杨静, 詹晓娟. 基于随机森林的特征选择算法. 吉林大学学报(工学版), 2014, 44(1): 137-141. YAO D J, YANG J, ZHAN X J. Feature selection algorithm based on random forest. Journal of Jilin University(Engineering and Technology Edition), 2014, 44(1): 137-141. |
| [17] |
VAPNIK V, LEVIN E, CUN Y L. Measuring the VC-Dimension of a learning machine. Neural Computation, 1994, 6(5): 851-876. DOI:10.1162/neco.1994.6.5.851 |
| [18] |
郭振洲, 刘然, 拱长青, 等. 基于灰狼算法的改进研究. 计算机应用研究, 2017, 34(12): 89-92. GUO Z Z, LIU R, GONG C Q, et al. Study on improvement of gray wolf algorithm. Application Research of Computers, 2017, 34(12): 89-92. |
| [19] |
HELALEH, A H, ALIZADEH M. Performance prediction model of Miscible Surfactant-CO2 displacement in porous media using support vector machine regression with parameters selected by Ant colony optimization. Journal of Natural Gas Science and Engineering, 2016, 30(1): 388-404. |
| [20] |
MIRJALILI S, MIRJALILI S M, LEWIS A. Grey wolf optimizer. Advances in Engineering Software, 2014, 69(3): 46-61. |
 2020, Vol. 32
2020, Vol. 32




