2. 中国地质大学 (北京)数理学院, 北京 100083;
3. 中国石油长庆油田分公司 第三采气厂, 西安 710016;
4. 中国石油长庆油田分公司 第五采气厂, 西安 710016
2. School of Science, China University of Geosciences(Beijing), Beijing 100083, China;
3. No.3 Gas Production Plant, PetroChina Changqing Oilfield Company, Xi'an 710016, China;
4. No.5 Gas Production Plant, PetroChina Changqing Oilfield Company, Xi'an 710016, China
致密砂岩储层具有低孔、低渗、强非均质性的地质特征,AVO正演分析是其研究过程中的一项重要的技术[1-2]。叠前地震AVO技术以Zoeppritz方程为理论基础,广泛应用于复杂油气藏的岩性和裂缝识别、油气检测等油气勘探领域[3]。Zoeppritz方程理论研究表明,AVO响应特征取决于反射界面两侧的弹性参数,然而,不同类型的岩性或流体的弹性参数存在一定的重叠,与反射界面相关的弹性参数并不能准确地确定反射界面两侧的岩性或者流体类型。因此,AVO正演模拟具有一定的不确定性,进而导致地震储层预测的多解性[4-5]。
近年来,国内外众多学者针对储层不确定性问题开展了相关研究,Richard[6]采用贝叶斯估计方法,定量表征了不同岩性弹性参数之间存在重叠、地震数据估计地震反射系数等2种不确定性问题,在此基础上全面表征AVO的岩性解释中的不确定性问题;陈建江等[7]采用贝叶斯方法,采用解析式手段描述了叠前地震AVO反演过程中参数估计的不确定性问题;何涛等[8]结合实验室测量和测井解释,采用Gassmann流体替换方法和Monte-Carlo随机正演方法,建立了参数不固定的岩石物理模型与地震AVO响应的关系;更多文章围绕着地震反演、横波预测等解释过程的不确定性问题开展研究[9-12]。
前人针对AVO正演过程中参数不确定问题开展较少,为此,以苏里格致密砂岩气藏的岩性资料及其岩石物理参数为基础,开展致密砂岩储层的AVO正演模拟过程中的不确定性研究,以期为储层预测提供有效的认识,从而降低致密砂岩气藏的开发风险。
1 AVO不确定性的表征方法针对AVO分析中的不确定性问题,主要采用信息熵和马尔科夫链蒙特卡罗模拟方法(MCMC,Markov Chain Monte Carlo)进行表征。信息熵主要用来表征测井参数及AVO参数的不确定性,MCMC方法主要用来穷尽岩性组合样本,使得样本更加丰富,解决测井解释数据的不完备性问题。
1.1 信息熵据文献[13]报到,信息熵是香农在1948年从热力学的热熵借用而来的,用于表征信息度量过程中的不确定性,解决了信息量化的问题,为信息论奠定了基础。
假设X为连续随机变量,其信息熵定义为
| $ H(X) = - \int_{ - \infty }^{ + \infty } p (x)\log [p(x)]{\rm{d}}x $ | (1) |
式中:H (X)是连续随机变量X的信息熵;p(x)是X的概率密度函数。
相应地,针对2个连续随机变量X和Y的信息熵,其定义为
| $ H(X, Y) = - \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {} p} (x, y)\log [p(x, y)]{\rm{d}}x{\rm{d}}y $ | (2) |
式中:p(x, y)是连续随机变量X和Y的联合概率密度函数。
相比均值、方差等统计学特征而言,信息熵方法综合考虑了数据的整体分布特征,同时能够表征连续性随机变量和类型变量中的不确定性问题,为不确定性的刻画提供了一种有效的统计学手段。
1.2 MCMC随机抽样方法不确定性源于不完整的信息,在对原始测井数据进行分析过程中,岩性组合模式及反射界面两侧弹性参数的选取都具有局限性,不能完全覆盖所有地层岩性组合模式,得不到完备的AVO响应特征。为此,根据研究区的纵波速度、横波速度和密度等参数分布特征,采用马尔科夫蒙特卡罗抽样方法得到更为丰富的不同岩性下的岩石物理参数,从而减少AVO正演模拟过程中的不确定性。
Metropolis等[14]在研究粒子系统的平稳性质时,提出了基于马尔科夫链的蒙特卡罗方法,据文献[15]报到,随后Hastings对该抽样算法进行改进,提出了常用的Metropolis-Hastings(M-H)算法。该算法的基础是已知一个形式简单的分布函数,并据此分布函数进行采样,通过一定的概率确定样本作为目标分布函数的近似样本。假设离散马尔可夫链的转移矩阵每个元素为q(i, j),目标概率分布函数为p(x),其具体的算法步骤如下:
(1)初始化t=0时刻马氏链初始状态Xt=x0,迭代终止条件为t=T;
(2)令t=t+1,从条件概率分布q(x|xt-1)中生成候选样本
(3)计算接受率α(xt-1,
| $ \alpha \left( {{x_{t - 1}}, \hat x} \right) = \min \left\{ {1, \frac{{p(\hat x)}}{{p\left( {{x_{i - 1}}} \right)}}\frac{{q\left( {{x_{t - 1}}\mid \hat x} \right)}}{{q\left( {\hat x\mid {x_{t - 1}}} \right)}}} \right\} $ | (3) |
(4)根据均匀分布函数,随机生成0~1的数u*;
(5)若u*≤α(xt-1,
(6)若t=T,则停止迭代该过程,否则继续重复执行步骤(2)—(5)。
1.3 工作流程图 1为详细表征AVO正演模拟过程中不确定性的研究流程,从原始数据中岩石物理参数的不确定性问题出发,以概率和信息熵等方法为手段,从岩石物理参数、AVO反射特征、AVO属性响应特征等3个角度研究AVO正演过程中的不确定性。最后以苏里格气田苏西地区测井数据为基础,详细地剖析了AVO正演模拟过程中参数的不确定性问题,为地震数据的AVO分析和储层预测提供先验认识。

|
下载原图 图 1 AVO正演模拟过程不确定性研究流程 Fig. 1 Workflow of uncertainty analysis for AVO forward modeling |
AVO正演模拟的基础是岩石物理参数数据,为剖析AVO的不确定性问题,从其源头开始分析,根据实测的岩石物理数据,统计原始岩石物理参数中存在的不确定性。根据苏里格气田苏西地区实测测井参数数据,通过测井解释得到1 377个不同岩性及不同含气性的成果数据,其中泥岩、干层占比为64.1%,气水同层、差气层和气层等3种含气性样本点的占比为31.9%,而水层发育较少,仅占5%。因此,AVO分析过程中以泥岩、干层、气水同层、差气层、气层等为重点研究样本。通过概率密度函数和信息熵等2个角度分析AVO模型参数,即不同岩性的纵波速度、横波速度、密度的不确定性特征[16-17]。
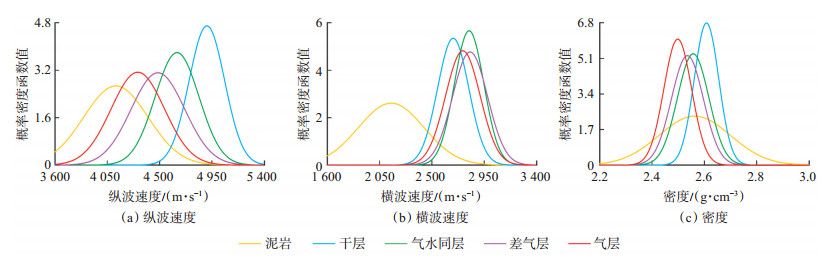
2.1 岩石物理参数概率密度函数根据岩石物理数据,对纵波速度、横波速度和密度参数进行统计分析,得到不同岩性的岩石物理参数的概率密度函数分布图。从图 2(a)中可以看出,纵波速度能够明显区分开砂岩和泥岩这2种岩性,砂岩的纵波速度多高于4 200 m/s,而泥岩的纵波速度多低于4 200 m/s,峰值集中分布在3 900~4 100 m/s。对于不同含气性的砂岩而言,随着含气饱和度的增加,其横波速度逐渐减小。虽然在不同含气性砂岩之间存在一定重叠,但其集中分布的区域有所差异,能够明显区分不同的含气砂岩;从图 2(b)中可以看出,横波速度对岩性的区分相对较好,泥岩的横波速度多低于2 500 m/s,集中分布为2 100~2 300 m/s,而砂岩的横波速度则多高于2 700 m/s,尽管砂泥岩在横波速度上表现出一定的重叠,但重叠样本数占比小于20%。横波速度概率密度函数图表明横波数据表征了岩石的基质特征,而这种现象带来的负面影响就是横波速度对砂岩含气性的区分度明显不如纵波速度[图 2(b)]。相对纵波速度图[图 2(a)]而言,气层、差气层和干层在横波速度上[图 2(b)]重叠度较高。从图 2(c)中可以看出,砂岩和泥岩在概率密度函数分布图上重合较多,泥岩的密度总体上略大于砂岩,且与干层的密度大小相当,其峰值和分布主体基本重叠,而含气砂岩的密度分布主体则略低于泥岩和干层。
|
下载原图 图 2 不同岩性岩石物理参数概率密度函数分布 Fig. 2 Distribution of probability density function of petrophysics parameters with different lithology |
分析表明,纵波速度、横波速度和密度等3种参数在不同岩性上具有差异性(图 2),尽管不同岩性或含气性之间存在一定的重叠,致使岩性和含气性的识别结果存在多解性,还是可以根据横波速度对岩性的敏感性和纵波速度对含气性的敏感性,计算纵横波速度比、泊松比、岩性和流体敏感因子等岩石物理参数,来降低岩石物理参数表征岩性、含气性的不确定及多解性。
2.2 岩石物理参数信息熵特征从信息论角度,采用信息熵的方法描述岩石物理参数的不确定性。根据岩石物理参数数据,计算不同岩性的纵波速度、横波速度和密度等参数的信息熵,得到不同岩性3种参数的信息熵变化趋势(图 3)。可以看出,当分割区间数<40时,不同岩性的岩石物理参数信息熵基本重叠,且随着区间划分段数的增加,各岩性纵波速度、横波速度和密度的信息熵快速增大,当区间数>40时,信息熵的值变化幅度减弱,当区间数达到120时变化微小,趋于平稳。

|
下载原图 图 3 不同岩性岩石物理参数信息熵变化趋势 Fig. 3 Variation trend of information entropy of petrophysics parameters with different lithology |
对于纵波速度而言[图 3(a)],在划分区间数较大时,泥岩的信息熵明显高于砂岩,对于不同含气性的砂岩而言,气层和差气层的信息熵趋势基本重叠,干层的信息熵高于其他3种不同含气性砂岩,气水同层的信息熵最低。所以,采用纵波速度识别不同岩性时,泥岩的不确定性大于砂岩,干层的不确定性高于其他3种含气砂岩。图 3(b)为横波速度信息熵变化趋势,其表现出和纵波速度相同的现象。相比纵波速度和横波速度而言,泥岩密度的信息熵低于气层和差气层,但大于干层和气水同层[图 3(c)]。
信息熵变化趋势表明,纵波速度、横波速度和密度等3种岩石物理参数对不同的岩性或含气性具有一定的指示作用,同时这种指示作用存在很大的不确定性。
3 AVO正演中的不确定性据文献[18]报到,AVO基础理论是Zoeppritz于1919年推导出的Zoeppritz方程,主要参数为纵波速度、横波速度和密度。上文从概率和信息熵等2个角度分析了纵波速度、横波速度和密度这3种岩石物理参数的不确定性及其进一步导致AVO正演的不确定性。为此,根据测井数据统计的不同岩性的反射界面,分析正演模型参数反射界面上下介质纵波速度比、横波速度比、密度比对正演模拟结果的影响。并采用MCMC随机抽样方法丰富研究目标不同的岩性组合,得到不同岩性反射界面下的AVO反射特征和AVO属性响应特征,从多个角度进一步分析AVO正演模拟过程中的不确定性问题。
3.1 AVO正演模型参数的不确定性Zoeppritz方程精确地表征了反射系数、透射系数和反射界面上下岩石物理参数与入射角变化之间的关系,反射界面上下层介质的纵波速度、横波速度和密度参数决定了界面纵波反射系数随入射角的变化特征[19-20]。以泥岩-气层的两层介质建立简化的AVO正演模型,上层介质和下层介质的岩石物理参数分别为Vp1,Vs1,ρ1和Vp2,Vs2,ρ2,分析上下层介质岩石物理参数Vp2/Vp1,Vs2/Vs1和ρ2/ρ1变化时对正演模拟结果的影响,以此分析AVO正演模拟过程中的不确定性。
(1)Vp2/Vp1的影响
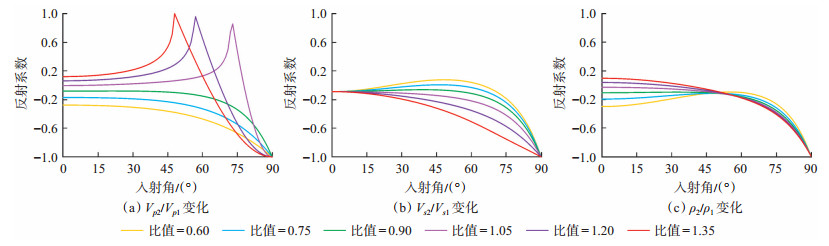
为了分析Vp2/Vp1对AVO正演的影响,通过改变反射界面上下层介质的纵波速度比值Vp2/Vp1,分析反射系数随入射角的变化特征。为此,设置6种AVO正演模型,采用Zoeppritz方程得到AVO反射系数随着入射角在Vp2/Vp1下增大的变化趋势[图 4(a)]。结果表明:AVO正演结果在Vp2/Vp1为1的前后出现2种明显不同的结果,当Vp2/Vp1<1时,纵波反射系数随着入射角的增加逐渐减小,反射系数表现为负梯度特征,且随着Vp2/Vp1的增加,其反射系数的变化梯度逐渐增大;Vp2/Vp1 ≥ 1时,纵波反射系数表现出突增或突减的现象,在临界角出现转折点,不同的Vp2/Vp1,临界角不一致,且随着Vp2/Vp1增加,其转折点向左平移。
|
下载原图 图 4 模型参数对AVO正演的影响 Fig. 4 Influence of model parameters on AVO forward modeling |
(2)Vs2/Vs1的影响
为了分析Vs2/Vs1对AVO正演的影响,通过改变反射界面上下层介质的横波速度比值Vs2/Vs1,分析反射系数随入射角的变化特征。为此,设置6种AVO正演模型,采用Zoeppritz方程得到AVO反射系数随着入射角在Vs2/Vs1的变化趋势[图 4(b)]。结果表明,横波速度比值的变化不会影响AVO截距,6种反射系数在入射角为0°时,对应的反射系数是相同的。随着入射角的增加,纵波反射系数与Vs2/Vs1成反比趋势。当Vs2/Vs1>1时,纵波反射系数基本上为负值,且随入射角增加表现为负梯度特征;当Vs2/Vs1<1时,纵波反射系数在小角度范围内呈现出正梯度,在大角度范围内呈现为负梯度特征,整体表现为减小的趋势。
(3)ρ2/ρ1的影响
为了分析ρ2/ρ1对AVO正演的影响,通过改变反射界面上下层介质的密度比值ρ2/ρ1,分析反射系数随入射角的变化特征。为此,设置6种AVO正演模型,采用Zoeppritz方程得到AVO反射系数随着入射角在ρ2/ρ1下增大的变化趋势[图 4(c)]。结果表明,6种模型的纵波反射系数随着入射角的增加向负梯度方向变化。在临界角度以内,纵波反射系数随着ρ2/ρ1的减小而减小;当大于临界角时,纵波反射系数随着ρ2/ρ1的减小而增大,反射系数的梯度逐渐增大。
3.2 AVO响应特征的不确定性分析为了进一步分析AVO的响应特征,根据苏里格气田苏西地区1 377个测井解释成果数据,统计得到1 289个不同岩性介质的反射界面,重点分析上层介质为泥岩,下层介质为干层、气水同层、差气层和气层等4种反射界面的岩石物理模型。为了对比上层介质发生变化时,AVO响应特征的变化,改变上层介质,建立了上层介质为干层,下层介质为不同含气性(气水同层、差气层、气层)砂岩的3种典型组合的反射界面。建立的反射界面涵盖了不同岩性、不同含气性的介质,涉及到不同储层厚度和不同含气饱和度的特征,包含了研究区所有可能存在的反射界面组合类型,统计结果能够更准确地分析AVO特征。
根据测井资料得到的不同岩性介质的反射界面的统计结果,不同岩性介质反射界面组合是有限的,不能真实反映研究区实际的AVO响应。为此,根据泥岩-干层、泥岩-气水同层、泥岩-差气层、泥岩-气层、干层-气水同层、干层-差气层和差气层的分布特征,采用MCMC随机抽样法模拟不同岩性反射界面的组合模式,并得到上下反射界面的岩石物理参数。
3.2.1 AVO反射系数特征根据统计得到的7种典型反射界面,采用Zoeppritz方程计算纵波反射系数随入射角增大的变化,并采用概率密度函数,分析不同入射角度下,储层内部岩性、含气性发生变化时,AVO响应特征及其不确定性[21]。图 5为计算得到的不同岩性、含气性介质反射界面组合模式下的AVO反射系数概率密度函数。

|
下载原图 图 5 不同岩性反射界面组合模式下的AVO反射系数概率密度函数 Fig. 5 Probability density function of AVO reflection coefficient with different lithology reflection interface |
[图 5(a)—(d)]是上层介质为泥岩时得到的AVO反射系数概率密度函数。结果表明,当上层介质为泥岩,下层介质变化时,入射角为25°~55°时,反射系数分布较为集中,且当下层介质不同时,其集中分布的区域也存在一定的差异,但不同含气性砂岩之间重叠范围较大,致使不同含气砂岩的AVO反射特性存在很大的不确定性。总体而言,AVO反射系数随着入射角的增大,其变化幅度增大,即在小角度范围内梯度变化较为缓慢,而大角度范围内,反射系数梯度表现为突降的特征。为了对比分析上层介质岩性不同时AVO反射系数的变化特征,设置了上层介质为干层,下层介质为气水同层、差气层和气层等3种反射界面,得到相应的AVO反射系数概率密度函数[图 5(e)—(g)]。结果显示,当上层介质为干层时,对于下层含水砂岩和含气砂岩的介质,反射系数基本上都在0值以下,具有负截距特征,且集中分布在-0.15~0。随着含气饱和度的增加,反射系数负向变化且梯度变化增大。
上层介质为泥岩或干层,下层介质为含气砂岩时,AVO响应特征明显,但与含水砂岩的响应特征存在大范围的重叠,对流体性质的预测精度较低,在实际应用中,很难达到有效识别烃类的目的。因此,单纯依据纵波反射系数与入射角度的变化关系开展储层岩性及含气性的预测具有多解性。
3.2.2 AVO属性特征截距(P)和梯度(G)均是AVO分析过程中的重要属性,对致密砂岩储层含气性特征具有一定的指示作用。截距反映了垂直入射时的反射系数,而梯度表征了振幅随入射角或炮检距变化的特征。通过分析不同组合界面下这2个参数的组合特征的变化,进而进行储层烃类的判识[22-24]。
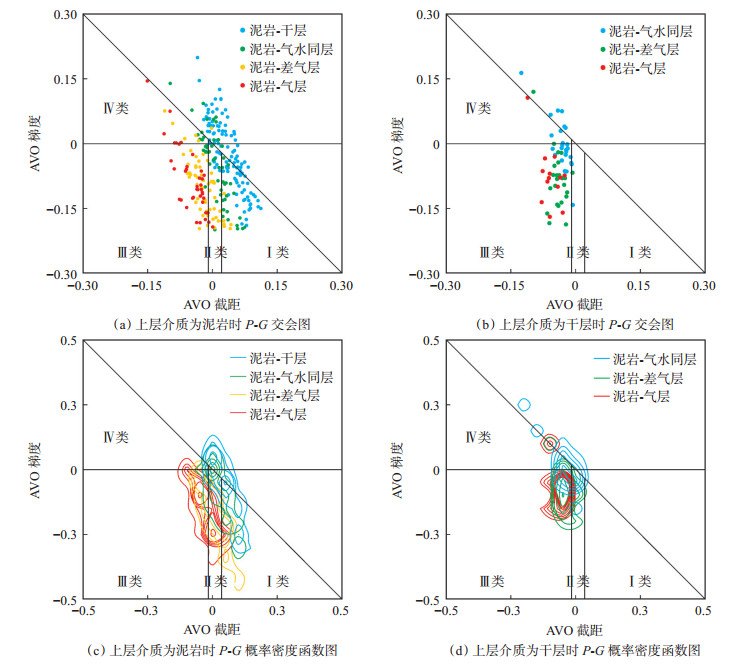
根据Zoeppritz近似方程计算AVO截距和梯度,得到上层介质分别为泥岩和干层时不同岩性组合界面的截距和梯度交会图[图 6(a)—(b)]。图 6(a)为上层介质为泥岩时,AVO截距和梯度的分布特征。从整体分布上看,不同岩性及含气性的截距和梯度属性分布范围较广,大部分样本点分布在背景趋势线以下。随着下层介质含气饱和度的增加,截距基本上为负值,梯度从正值向负值变化,截距和梯度交会点从第一象限过渡到第二象限,最终过渡到第三象限。部分泥岩-干层、少量泥岩-差气层的岩性界面组合模式落在第二类区域内,绝大部分泥岩-气层、泥岩-差气层岩性界面组合模式分布在第三象限内,具有第Ⅲ类AVO响应特征。图 6(b)为上层介质岩性变化时,不同含气性变化下的AVO截距和梯度特征。结果表明,当下层介质为含气流体时,91.89%的样本点分布表现出Ⅲ类AVO特征,落于第三象限内;当下层介质为气水混合流体时,同样以Ⅲ类AVO特征为主,存在7.69%的样本点落于第四象限内,整体上表现出Ⅲ类AVO特征。
|
下载原图 图 6 AVO截距和梯度特征分布 Fig. 6 Distribution of AVO intercept and gradient attribute |
为了进一步研究岩性发生变化时AVO的异常特征,根据MCMC抽样方法生成岩性序列以及对应的岩石物理参数,计算得到AVO截距和梯度,建立了截距和梯度的双变量概率密度函数图[图 6(c) —(d)],从图中可以看出,整体趋势与[图 6(a) —(b)]一致。当上层介质为泥岩时,气层、差气层与干层能够有效地区分开,但是与气水同层重叠度较高,多集中分布在第三象限内;当上层介质为干层时,3种岩性组合模式基本分布在第三象限,少量岩性组合模式表现出Ⅱ和Ⅳ类AVO特征。
根据得到的上层介质分别为泥岩和干层时的AVO截距和梯度属性,进一步从信息熵角度分析AVO截距和梯度参数的不确定性,采用式(2)计算截距和梯度属性的联合信息熵,计算结果如表 1所列。结果表明,对于上层介质为泥岩时,下层介质为砂岩的联合信息熵大于下层介质为泥岩,而对于上层介质为干层时,表现出相反的情况。下层介质为砂岩时,上层介质为干层的联合信息熵小于上层介质为泥岩的联合信息熵。根据信息熵的特征,当下层介质为砂岩时,上层介质为干层的AVO属性P,G的不确定性小于上层介质为泥岩时的不确定性。泥岩-干层界面AVO响应的不确定性最强,其次为干层-泥岩界面。
|
|
下载CSV 表 1 AVO截距和梯度不同岩性组合反射界面联合信息熵 Table 1 Joint information entropy of AVO intercept and gradient with different lithology reflecting interface |
上述过程中从定性、半定量角度分析了AVO正演模拟过程中的不确定性,下一步可以根据叠前地震资料提取的AVO截距和梯度属性,采用多参数概率融合方法得到目标区含气性概率信息,从定量角度量化AVO分析过程的不确定性。
4 结论(1)虽然AVO正演的不确定性导致地震储层的预测也具有很强的多解性,也导致对储层中流体的判识存在较大风险,但是AVO正演不确定的研究还是能够提供先验认识,有效降低这些风险,提高决策的优化度。
(2)以概率密度、信息熵等技术为手段表征测井原始数据中存在的不确定性因素,提供了岩石物理模型不确定性研究的数据基础。在用MCMC随机抽样方法丰富原始解释数据中不同的岩性组合模式下,分析各组合模式下不同岩石物理参数存在的不确定性,奠定了AVO响应判识岩性和流体的基础。
(3)岩石物理参数概率密度和信息熵的研究表明,纵波速度、横波速度、密度等3种岩石物理参数能够区分不同的岩性及含气性,但是均存在一定的重叠,对岩性和含气性的判识存在多解性。根据3种参数计算得到的纵横波速度比、泊松比等岩石物理参数,可有效降低多解性。
(4)AVO反射特征表明上下层介质Vp2/Vp1,Vs2/Vs1和ρ2/ρ1的变化导致AVO反射系数随入射角增大的变化特征存在差异,且上下层介质不同岩性组合反射界面下,其AVO反射特征之间存在重叠区域,都有相对的不确定性存在。AVO截距和梯度特征表明上层介质为干层或泥岩时AVO响应特征类似,且变化趋势一致,随着下层介质含气饱和度的增加,AVO截距和AVO梯度从第一象限过渡到第三象限。
| [1] |
杨华, 付金华. 苏里格大型致密砂岩气藏形成条件及勘探技术. 石油学报, 2012, 33(增刊1): 27-36. YANG H, FU J H. Formation conditions and exploration technology of large-scale tight sandstone gas reservoir in Sulige. Acta Petrolei Sinica, 2012, 33(Suppl 1): 27-36. |
| [2] |
郭艳琴, 何子琼, 郭彬程, 等. 苏里格气田东南部盒8段致密砂岩储层特征及评价. 岩性油气藏, 2019, 31(5): 1-11. GUO Y Q, HE Z Q, GUO B C, et al. Reservoir characteristics and evaluation of tight sandstone of He 8 member in southeastern Sulige Gas Field, Ordos Basin. Lithologic Reservoirs, 2019, 31(5): 1-11. |
| [3] |
潘仁芳, 赵玉华, 史松群. 苏里格庙气田盒8段砂岩AVO正演模型研究. 天然气工业, 2002, 22(5): 7-10. PAN R F, ZHAO Y H, SHI S Q. Study on the AVO forward modeling of sandstone He-8, Permian, Shuligemiao gas field. Natural Gas Industry, 2002, 22(5): 7-10. |
| [4] |
王家华, 赵巍. 基于统计岩石物理学的直接岩石物理反演. 复杂油气藏, 2010, 3(4): 6-8. WANG J H, ZHAO W. Direct rock physics inversion based on statistical rock physics. Complex Hydrocarbon Reservoirs, 2010, 3(4): 6-8. |
| [5] |
MICHAEL R, STAN E D, LAURENS B. Uncertainty estimation for amplitude variation with offset(AVO)inversion. Geophysics, 2003, 68(5): 1485-1496. DOI:10.1190/1.1620621 |
| [6] |
RICHARD T H. Quantifying the uncertainty in an AVO interpretation. Geophysics, 2002, 67(1): 117-125. |
| [7] |
陈建江, 朱兴卉. AVO反演的不确定性分析. 地球物理学进展, 2009, 24(4): 1461-1467. CHEN J J, ZHU X H. Uncertainty analysis for AVO inversion. Progress in Geophysics(in Chinese), 2009, 24(4): 1461-1467. |
| [8] |
何涛, 史謌, 邹长春, 等. 砂岩储层AVO特征影响因素的不确定性研究. 地球物理学报, 2011, 54(6): 1584-1591. HE T, SHI G, ZOU C C, et al. The uncertainty analysis of the key factors that affect the AVO attributes in sandstone reservoir. Chinese Journal of Geophysics, 2011, 54(6): 1584-1591. |
| [9] |
FERNANDEZ-MARTINEZ J L. Model reduction and uncertainty analysis in inverse problems. The Leading Edge, 2015, 34(9): 1006-1016. DOI:10.1190/tle34091006.1 |
| [10] |
BOSCH M, BERTORELLI G, ALVAREZ G, et al. Reservoir uncertainty description via petrophysical inversion of seismic data. The Leading Edge, 2015, 34(9): 1018-1026. DOI:10.1190/tle34091018.1 |
| [11] |
BALL V, LUIS T, CHRISTIAN S, et al. Uncertainty in inverted elastic properties resulting from uncertainty in the low-frequency model. The Leading Edge, 2015, 34(9): 1028-1035. DOI:10.1190/tle34091028.1 |
| [12] |
GORAIN S, SHALIVAHAN, PRABHAKAR T. Uncertainty in attribute-based inversion for quantification of the estimation of stock-tank oil initially in place in Kalol reservoir, Cambay Basin, India. The Leading Edge, 2015, 34(9): 1058-1063. DOI:10.1190/tle34091058.1 |
| [13] |
路大金. 随机过程及其应用. 北京: 清华大学出版社, 1986: 1-20. LU D J. Stochastic processes with applications. Beijing: Tsinghua University Press, 1986: 1-20. |
| [14] |
M ETROPOLIS N, ULAM S. The Monte Carlo method. Journal of the American Statistical Association, 1949, 44(247): 335-341. DOI:10.1080/01621459.1949.10483310 |
| [15] |
盛骤, 谢式千, 潘承毅. 概率论与数理统计. 北京: 高等教育出版社, 1979: 300-333. SHENG Z, XIE S Q, PAN C Y. Probability and statistics. Beijing: Higher Education Press, 1979: 300-333. |
| [16] |
高世臣, 张丹. 多参数概率融合法在叠前地震储层预测中的应用:以苏里格气田苏194区块为例. 油气地质与采收率, 2015, 22(6): 61-67. GAO S C, ZHANG D. Application of multi-parameter probability fusion method to pre-stack seismic reservoir prediction:a case study of Su194 block in Sulige Gas Field. Petroleum Geology and Recovery Efficiency, 2015, 22(6): 61-67. |
| [17] |
彭达, 肖富森, 冉崎, 等. 基于KT模型流体替换的岩石物理参数反演方法. 岩性油气藏, 2018, 30(5): 82-90. PENG D, XIAO F S, RAN Q, et al. Inversion of rock physics parameters based on KT model fluid substitution. Lithologic Reservoirs, 2018, 30(5): 82-90. |
| [18] |
王秀姣, 黄家强, 姜仁, 等. AVO不同含气砂岩的AVO响应类型及其近似式误差分析. 岩性油气藏, 2017, 29(5): 120-126. WANG X J, HUANG J Q, JIANG R, et al. AVO response of different types of gas-bearing sandstone and error analysis of approximate formulas. Lithologic Reservoirs, 2017, 29(5): 120-126. |
| [19] |
WANG X C, PAN D Y. Application of AVO attribute inversion technology to gas hydrate identification in the Shenhu area, South China Sea. Marine and Petroleum Geology, 2017, 80: 23-31. DOI:10.1016/j.marpetgeo.2016.11.015 |
| [20] |
郭强, 张宏兵, 曹呈浩, 等. Zoeppritz方程叠前多参数反演及密度敏感性分析. 石油地球物理勘探, 2017, 52(6): 105-112. GUO Q, ZHANG H B, CAO C H, et al. Density-sensitivity analysis about prestack multi-parameter inversion based on the exact Zoeppritz equation. Oil Geophysical Prospecting, 2017, 52(6): 105-112. |
| [21] |
周华建. 基于叠前OVT域偏移的河道砂体预测方法. 岩性油气藏, 2019, 31(4): 112-120. ZHOU H J. Prediction method of channel sand body based on prestack migration in OVT domain. Lithologic Reservoirs, 2019, 31(4): 112-120. |
| [22] |
张艳, 张春雷, 高世臣. 基于SOM和HSV染色技术的致密砂岩储层地震相分析. 天然气地球科学, 2018, 29(2): 259-267. ZHANG Y, ZHANG C L, GAO S C. Seismic facies analysis of tight sandstone reservoir based on SOM and HSV color technique. Natural Gas Geoscience, 2018, 29(2): 259-267. |
| [23] |
SHUEY R T. A simplification of the Zoeppritz equations. Geophysics, 1985, 50(4): 609-614. DOI:10.1190/1.1441936 |
| [24] |
HOSSEINI-SHOAR B, JAVAHERIAN A, KESHAVARZ-FARAJKHAH N, et al. Reflectivity template, a quantitative interceptgradient AVO analysis to study gas hydrate resources:a case study of Iranian deep sea sediments. Marine and Petroleum Geology, 2014, 51: 184-196. DOI:10.1016/j.marpetgeo.2013.12.007 |
 2020, Vol. 32
2020, Vol. 32



