2. 中国石油长庆油田分公司 千口气井评价挖潜工程项目组, 西安 710018;
3. 中国石油大学 (华东)地球科学与技术学院, 山东 青岛 266580;
4. 中国石油长庆油田分公司 勘探开发研究院, 西安 710018
2. Project Group for Evaluation and Excavation of Qiankou Gas Well, PetroChina Changqing Oilfield Company, Xi'an 710018, China;
3. School of Geosciences, China University of Petroleum(East China), Qingdao 266580, Shandong, China;
4. Research Institute of Exploration and Development, PetroChina Changqing Oilfield Company, Xi'an 710018, China
识别和评价储层含气性是测井解释工作的关键[1],致密砂岩含气储层岩性复杂、孔隙结构复杂,孔隙度较低、渗透性能较差、含气饱和度较低,常规测井资料易受岩石骨架影响[2-3],孔隙流体对其响应特征的贡献小,测井曲线难以有效突出反映孔隙流体的信息,导致气层识别难度较大[4-6]。通常,利用基于常规测井的三孔隙度重叠法、孔隙度背景值及声波时差等来识别气层,这些方法在应用上都具有局限性,而阵列声波测井能够提供反映地层骨架和流体特征的声学信息,如纵横波速度比等运动学参数,泊松比、体积模量等弹性力学参数以及频谱信息[7-9],这些声学信息对致密储层的含气性敏感程度很高,可用于判别储层的流体性质。
鄂尔多斯盆地东部横跨伊陕斜坡和晋西挠褶带两大构造单元,该地区上古生界致密砂岩储层属于典型的岩性气藏,受北部物源和沉积环境的影响,主要发育浅水海相三角洲或者浅水湖相三角洲砂体,岩石类型主要为石英砂岩、岩屑石英砂岩,储层物性差、孔隙结构复杂、岩石矿物组分多样、流体识别困难。针对这一难题,基于Xu-White模型,利用阵列声波测井资料提取的纵、横波速度数据,结合Biot-Gassmann方程和饱和度流体替换模型,通过获取能够反映地层流体的含气敏感参数纵横波速比差值、体积模量差值以及含气指示因子等指标,建立一种识别致密砂岩气层的新方法,以期能够有效地评价鄂尔多斯盆地东部上古生界致密砂岩储层的含气性。
1 理论基础 1.1 等效介质弹性模量估算模型 1.1.1 Hashin-Shtrikman界限在进行等效模量预测时,通常假设地层是均匀各向同性的,Hashin-Shtrikman界限(HS界限)能预测几种矿物所组成的岩样弹性模量范围[10],具体的值依赖于孔隙的几何形状,界限的大小也依赖于不同组分本身性质的差异,差异越大,预测结果就越差。当混合项为2种构成成分时,体积模量K与剪切模量μ的上下界分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{K^{{\rm{HS}} \pm }} = {K_1} + \frac{{{f_2}}}{{{{\left( {{K_2} - {K_1}} \right)}^{ - 1}} + {f_1}{{\left( {{K_1} + 4{\mu _1}/3} \right)}^{ - 1}}}}}\\ {{\mu ^{{\rm{HS}} \pm }} = {\mu _1} + \frac{{{f_2}}}{{{{\left( {{\mu _2} - {\mu _1}} \right)}^{ - 1}} + \frac{{2{f_1}\left( {{K_1} + 2{\mu _1}} \right)}}{{5{\mu _1}\left( {{K_1} + 4{\mu _1}/3} \right)}}}}} \end{array}} \right. $ | (1) |
式中:f为各构成成分的体积分数;HS ±分别为Hashin-Shtrikman界限的上界和下界。
当混合项构成成分超过2种时,则须要进行加权平均,Berryman[11]给出了一种适用于多种成分混合的计算公式
| $\left\{ {\begin{array}{*{20}{l}} {{K^{{\rm{HS}} + }} = \Lambda \left( {{\mu _{\max }}} \right),{K^{{\rm{HS}}-}} = \Lambda \left( {{\mu _{\min }}} \right)}\\ {{\mu ^{{\rm{HS}} + }} = \Gamma \left[ {\xi \left( {{K_{\max }},{\mu _{\max }}} \right)} \right],{\mu ^{{\rm{HS}}-}} = \Gamma \left[ {\xi \left( {{K_{\min }},{\mu _{\min }}} \right)} \right]} \end{array}} \right. $ | (2) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\Lambda (x) = < \frac{1}{{K(i) + \frac{{4x}}{3}}}{ > ^{ - 1}} - \frac{{4x}}{3}}\\ {\Gamma (x) = < \frac{1}{{\mu (i) + x}}{ > ^{ - 1}} - x}\\ {\xi (K, \mu ) = \frac{{\mu (9K + 8\mu )}}{{6(K + 2\mu )}}} \end{array}} \right. $ | (3) |
式中:<·>为各组分的平均值,即对各组分按其体积分数求加权平均;i为混合项超过2种时各构成成分的编号,分别取1,2,3…
1.1.2 Voigt和Reuss界限Voigt和Reuss界限[12]的理论计算方法比较简单,类似于电路中的串并联模型。N种成分的等效弹性模量的Voigt上限MV为
| $ {M_{\rm{v}}} = \sum\limits_{i = 1}^N {{f_i}} {M_i} $ | (4) |
Voigt平均也称等应变平均,它给出了当各构成成分假设有相等的应变时,平均应力和平均应变的比,而Reuss下限MR为
| $ \frac{1}{{{M_{\rm{R}}}}} = \sum\limits_{i = 1}^N {\frac{{{f_i}}}{{{M_i}}}} $ | (5) |
Reuss界限也称等应力平均,给出了当各构成成分假设有相等的应力时,平均应力和平均应变的比。
1.1.3 Voigt-Reuss-Hill平均模型Voigt平均和Reuss平均公式中的MV,MR可以表示任何弹性模量,但最有意义的是用来表示体积模量和剪切模量,然后再由这2个模量计算其他的弹性参数。
Voigt-Reuss-Hill平均(V-R-H平均)模型[13]是将Voigt上限和Reuss下限求取算术平均,从而确定混合介质的等效弹性模量,其表达式为
| $ {M_{{\rm{VRH}}}} = \frac{{{M_{\rm{V}}} + {M_{\rm{R}}}}}{2} $ | (6) |
当给定岩石的成分和孔隙空间时,V-R-H平均可以用来估算岩石的等效弹性模量,在实际中通常也是应用最广泛的一种等效弹性模量计算方法。
通过对不同的等效介质弹性模量估算模型与鄂尔多斯盆地东部上古生界致密砂岩储层的岩心实验数据进行对比与分析,可知当2种物质进行混合时,HS界限、Voigt界限和Reuss界限只是给出了不同物质混合时的上下限,在实际应用中混合物质是不可能达到极限状态的,而V-R-H平均模型给出了Voigt上限和Reuss下限的算术平均值,与实际情况更相符(图 1)。
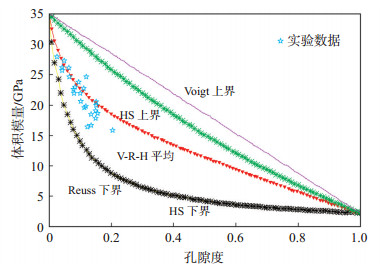
|
下载原图 图 1 等效介质弹性模量估算模型对比 Fig. 1 Comparison of elastic modulus estimating models of equivalent medium |
在有关岩石物理的研究中,绝大多数是以BiotGassmann理论为基础的,Biot[14]推导出用岩石骨架性质预测流体饱和岩石中的速度理论公式,该公式包含了岩石矿物骨架与孔隙流体之间的黏性和惯性相互作用机制。Gassmann[15]假设相同的矿物模量和孔隙空间各向同性,对孔隙的几何形体没有要求。在低频情况下,对于纵、横波速度的计算,Biot公式与Gassmann方程预测的结果相同。通常,利用Biot-Gassmann方程有2种假设:①假定饱和岩石和干岩石的剪切模量相同;②假定饱和岩石与干岩石的体积模量不同。该方程预测了岩石饱和流体后有效体积模量的增加,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{s}}} = {K_{\rm{d}}} + {\beta ^2}M}\\ {{\mu _{\rm{s}}} = {\mu _{\rm{d}}}} \end{array}} \right. $ | (7) |
其中
| $ \frac{1}{M} = \frac{{\beta - \mathit{\Phi }}}{{{K_{{\rm{ma}}}}}} + \frac{\mathit{\Phi }}{{{K_{\rm{n}}}}}, \beta = 1 - \frac{{{K_{\rm{d}}}}}{{{K_{\rm{m}}}}} $ | (8) |
将式(8)代入式(7)中,可以得到
| $ {K_{\rm{s}}} = {K_{\rm{d}}} + \frac{{{{\left( {1 - \frac{{{K_{\rm{d}}}}}{{{K_{\rm{m}}}}}} \right)}^2}}}{{\frac{\mathit{\Phi }}{{{K_{\rm{f}}}}} + \frac{{1 - \mathit{\Phi }}}{{{K_{\rm{m}}}}} - \frac{{{K_{\rm{d}}}}}{{K_{\rm{m}}^2}}}} $ | (9) |
相对应的纵、横波速度理论公式为
| $ {v_{\rm{p}}} = \sqrt {\frac{{{K_{\rm{s}}} + \frac{4}{3}{\mu _{\rm{s}}}}}{\rho } = } \sqrt {\frac{{{K_{\rm{d}}} + \frac{4}{3}{\mu _{\rm{s}}} + {\beta ^2}M}}{\rho }} , {v_{\rm{s}}} = \sqrt {\frac{{{\mu _{\rm{s}}}}}{\rho }} = \sqrt {\frac{{{\mu _{\rm{d}}}}}{\rho }} $ | (10) |
式中:Ks,Km,Kd,Kfl分别为岩石饱和流体、岩石基质、干岩石骨架、孔隙流体的体积模量,GPa;μs,μd分别为岩石饱和流体、干岩石骨架的剪切模量,GPa;β为Biot系数,表示水的压力为常数的条件下,流体体积变化与地层体积变化之比;M为模量,表示在地层体积保持不变的前提下,把流体压入地层时所需的压力,GPa;Φ为总孔隙度;ρ为地层岩石密度,g/cm3。
1.3 Xu-White模型Xu等[16-17]基于Kuster-Toksoz理论、Gassmann方程及有效差分介质(DEM)理论提出了一种利用孔隙度和泥质含量估算纵、横波速度的砂泥岩混合介质模型,即Xu-White模型。该模型假定岩石的总孔隙空间由与砂岩颗粒和泥岩颗粒(包含束缚水)相关的孔隙组成(图 2)。
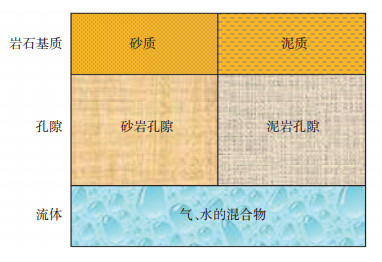
|
下载原图 图 2 Xu-White模型 Fig. 2 Xu-White model |
Xu-White模型综合考虑了岩石基质性质、孔隙大小、孔隙形状以及孔隙流体性质的影响,其基本特征是认为这2种孔隙空间的几何形状(孔隙纵横比)差异较大,砂岩孔隙纵横比较大,泥岩孔隙纵横比较小,因而对弹性模量的影响也不一样。孔隙空间按照砂岩、泥岩体积各自所占体积分数进行分配,即
| $ \mathit{\Phi } = {\mathit{\Phi }_{{\rm{sand }}}} + {\mathit{\Phi }_{{\rm{clay }}}}, {\mathit{\Phi }_{{\rm{sand }}}} = {\varphi _{{\rm{sand }}}}\frac{\mathit{\Phi }}{{1 - \mathit{\Phi }}}, {\mathit{\Phi }_{{\rm{clay }}}} = {\varphi _{{\rm{clay }}}}\frac{\mathit{\Phi }}{{1 - \mathit{\Phi }}} $ | (11) |
式中:Φ,Φsand,Φclay分别为总孔隙度,砂岩孔隙度和泥岩(黏土)孔隙度;φsand和φclay分别为砂岩和泥岩体积分数。
Kuster等[18]基于长波一阶散射理论,考虑夹杂体弹性性质、体积百分比和形状对介质弹性的影响,确定了两相介质的等效弹性模量。通过DEM理论,扩展了K-T理论中关于孔隙度远远小于孔隙纵横比的假设[19],从而求取某一确定孔隙度下干岩石骨架的体积模量和剪切模量为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{d}}} - {K_{\rm{m}}} = \frac{1}{3}\left( {{K^\prime } - {K_{\rm{m}}}} \right)\frac{{3{K_{\rm{d}}} + 4{\mu _{\rm{m}}}}}{{3{K_{\rm{m}}} + 4{\mu _{\rm{m}}}}}\sum\limits_{l = {\rm{ sand, clay }}} \quad {\mathit{\Phi }_l}{T_{iijj}}\left( {{\alpha _l}} \right)}\\ {{\mu _{\rm{d}}} - {\mu _{\rm{m}}} = \frac{{\left( {{\mu ^\prime } - {\mu _{\rm{m}}}} \right)}}{5}\frac{{6{\mu _{\rm{d}}}\left( {{K_{\rm{m}}} + 2{\mu _{\rm{m}}}} \right) + {\mu _{\rm{m}}}\left( {9{K_{\rm{m}}} + 8{\mu _{\rm{m}}}} \right)}}{{5{\mu _{\rm{m}}}\left( {3{K_{\rm{m}}} + 4{\mu _{\rm{m}}}} \right)}}\sum\limits_{l = {\rm{ sand, clay }}} {{\mathit{\Phi }_l}} F\left( {{\alpha _l}} \right)}\\ {F(\alpha ) = {T_{ijij}}(\alpha ) - \frac{{{T_{iijj}}(\alpha )}}{3}} \end{array}} \right. $ | (12) |
式中:Km,Kd,K′分别为岩石基质、干岩石骨架和孔隙介质的体积模量,GPa;μd,μm,μ′分别为岩石基质、干岩石骨架和孔隙介质的剪切模量,GPa。其中对于干岩石,K′和μ′等于0;αsand和αclay分别为砂岩和泥岩孔隙纵横比,通常情况下,对于纯砂岩孔隙αsand取0.12,泥岩孔隙αclay取0.035;Tijij (α)和F (α)是从Eshelby张量Tijkl中推导出的关于孔隙纵横比的函数[20-21]。
为了简化计算,Key等[22]假定干岩石骨架的泊松比不随孔隙度变化,将上述求解问题转换成一个线性常微分方程组的求解问题,干岩石骨架弹性模量表达为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{d}}} = {K_{\rm{m}}}{{(1 - \mathit{\Phi })}^p}}\\ {{\mu _{\rm{d}}} = {\mu _{\rm{m}}}{{(1 - \mathit{\Phi })}^q}} \end{array}} \right. $ | (13) |
式中:p和q为假设干岩石骨架泊松比为常数时的一组只与孔隙纵横比有关而与孔隙度无关的系数,且
含气饱和度声波岩石物理模型有很多,一直以来,流体替换大多数都是采用基于Wood方程的Gassmann流体替换方法的并联原理[23],即
| $ \frac{1}{{{K_{\rm{fl}}}}} = \frac{{{S_{\rm{w}}}}}{{{K_{\rm{w}}}}} + \frac{{1 - {S_{\rm{w}}}}}{{{K_{\rm{g}}}}} $ | (14) |
Brie等[24]利用Gassmann方程对含气储层声学特征进行分析和现场应用,提出来一个随含气饱和度变化的经验公式,即Brie公式
| $ {K_{\rm{fl}}} = \left( {{K_{\rm{w}}} - {K_{\rm{g}}}} \right)S_{\rm{w}}^e + {K_{\rm{g}}} $ | (15) |
式中:Kfl,Kg,Kw分别为地层孔隙流体、天然气和地层水的体积模量,GPa;Sw为地层含水饱和度,%;e为地区经验参数,通常为2~5,当e = 1时,上式可简化为串联模型;当e = 40时,上式近似等于并联模型,即Wood方程。
利用流体替换公式,考虑流体性质的影响,可以计算获得1-Sw作为指示气层的标志,1-Sw越大,气层显示越好。
2 评价方法 2.1 岩石骨架参数的确定(1)利用V-R-H平均模型计算岩石混合基质体积模量Km和剪切模量μm
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{\rm{m}}} = \frac{{{K_{\rm{V}}} + {K_{\rm{R}}}}}{2}}\\ {{\mu _{\rm{m}}} = \frac{{{\mu _{\rm{V}}} + {\mu _{\rm{R}}}}}{2}} \end{array}} \right. $ | (16) |
式中:
(2)利用简化的Xu-White模型[式(13)]计算干岩石骨架的体积模量Kd和剪切模量μd,模型中所选取的岩石基质和流体相关参数及取值如表 1所列。
|
|
下载CSV 表 1 鄂尔多斯盆地东部致密砂岩储层计算模型岩石基质和流体相关参数及取值 Table 1 Parameters of rock matrix and fluid in the calculation model for tight sandstone reservoir in eastern Ordos Basin |
(1)含气敏感参数的确定。利用上述方法确定的岩石骨架参数,通过Biot-Gassmann方程预测100%饱含水的地层的体积模量和剪切模量,即
| $ \left\{ {\begin{array}{*{20}{l}} {{K_{{\rm{sw}}}} = {K_{\rm{d}}} + \frac{{{{\left( {1 - \frac{{{K_{\rm{d}}}}}{{{K_{\rm{m}}}}}} \right)}^2}}}{{\frac{\mathit{\Phi }}{{{K_{\rm{w}}}}} + \frac{{1 - \mathit{\Phi }}}{{{K_{\rm{m}}}}} - \frac{{{K_{\rm{d}}}}}{{K_{\rm{m}}^2}}}}}\\ {{\mu _{{\rm{sw}}}} = {\mu _{\rm{d}}}} \end{array}} \right. $ | (17) |
利用体积模量与纵、横波速度的关系式[式(10)],结合式(17),预测100%饱含水地层的纵横波速度比为
| $ {R_{{\rm{sw}}}} = \frac{{{K_{{\rm{sw}}}}}}{{{\mu _{{\rm{sw}}}}}} + \frac{4}{3} = \frac{{{K_{{\rm{sw}}}}}}{{{\mu _{\rm{d}}}}} + \frac{4}{3} $ | (18) |
将100%饱含水地层的体积模量和纵横波速度比分别与实际测井资料获得的地层体积模量Ks和纵横波速度比Rs作差值,则
| $ {\Delta K = {K_{{\rm{sw}}}} - {K_{\rm{s}}} = {K_{\rm{d}}} + \frac{{{{\left( {1 - \frac{{{K_{\rm{d}}}}}{{{K_{\rm{m}}}}}} \right)}^2}}}{{\frac{\mathit{\Phi }}{{{K_{\rm{w}}}}} + \frac{{1 - \mathit{\Phi }}}{{{K_{\rm{m}}}}} - \frac{{{K_{\rm{d}}}}}{{K_{\rm{m}}^2}}}} - \rho \left( {v_{\rm{p}}^2 - \frac{4}{3}v_{\rm{s}}^2} \right)} $ | (19) |
| $ {\Delta R = {R_{{\rm{sw}}}} - {R_{\rm{s}}} = \frac{{{K_{{\rm{sw}}}}}}{{{\mu _{\rm{d}}}}} + \frac{4}{3} - \frac{{{v_{\rm{p}}}}}{{{v_{\rm{s}}}}}} $ | (20) |
若岩石体积模量差值ΔK和纵横波速度比差值ΔR均大于0,则判断为孔隙含气的影响,含气越多,影响越大。因此,可利用ΔK,ΔR作为气层识别的敏感参数指标。
(2)含气指示因子的确定。根据阵列声波测井资料计算获得的地层真实体积模量Ks,结合计算获得的干岩石骨架模量以及Biot-Gassmann方程[式(9)],可得地层孔隙流体体积模量Kfl为
| $ {K_{\rm{fl}}} = \frac{\mathit{\Phi }}{{\left[ {\frac{{{{\left( {1 - \frac{{{K_{\rm{d}}}}}{{{K_{\rm{m}}}}}} \right)}^2}}}{{{K_{\rm{s}}} - {K_{\rm{d}}}}} + \frac{{{K_{\rm{d}}}}}{{K_{\rm{m}}^2}} - \frac{{1 - \mathit{\Phi }}}{{{K_{\rm{m}}}}}} \right]}} $ | (21) |
将式(21)代入流体替换模型[式(15)],定义含气指示因子SI为
| $ SI = 1 - {\left( {\frac{{{K_{{\rm{fl}}}} - {K_{\rm{g}}}}}{{{K_{\rm{w}}} - {K_{\rm{g}}}}}} \right)^{\frac{1}{e}}} $ | (22) |
应用上述理论研究方法,结合鄂尔多斯盆地东部上古生界致密砂岩储层的实际情况,利用阵列声波测井资料提取的纵、横波数据,通过预测100%饱含水地层体积模量和纵横波速度比与实际测井资料计算获得的体积模量和纵横波速度比进行对比,并确定含气敏感参数和含气指示因子等指标对8口井23个气层段进行了含气性评价,总体应用效果良好。经统计分析可知,体积模量差值和含气指示因子符合层数分别为22和23个,符合率均高于95%;纵横波速度比差值符合层数17个,符合率高于70%。相对而言,纵横波速度比差值识别气层效果较差,而体积模量差值和含气指示因子识别气层准确度均较高,应用效果较好(表 2);气层厚度对该方法的识别效果影响不大,23个气层厚度为1.8~ 16.4 m,平均为4.2 m,综合这3项指标能较好地识别不同厚度的气层,然而,在实际应用中,纵横波速度比差值会与体积模量差值和含气指示因子在同一气层段出现一定程度的不吻合,此时,纵横波速度比差值识别指标不作为识别气层的依据。
|
|
下载CSV 表 2 鄂尔多斯盆地东部致密砂岩储层含气性评价指标效果统计 Table 2 Gas-bearing property evaluation indexes of tight sandstone reservoir in eastern Ordos Basin |
图 3为研究区X井2 340~2 365 m段致密砂岩储层含气性评价成果图,在气层B和C段,含气敏感参数体积模量差值ΔK>0,纵横波速度比差值ΔR>0,含气指示因子SI>0,该方法很好地验证了天然气的存在,能够准确地识别致密砂岩气层;在干层A段,ΔK<0,ΔR<0,SI<0,表明该井段不含天然气。其中,该井C段孔隙度为8.10%,渗透率为0.438 mD,含气饱和度为65.25%,综合解释为气层,经生产测试验证,该层压裂后试气日产气6.252 0万m3/d,解释结论与试气结果一致。
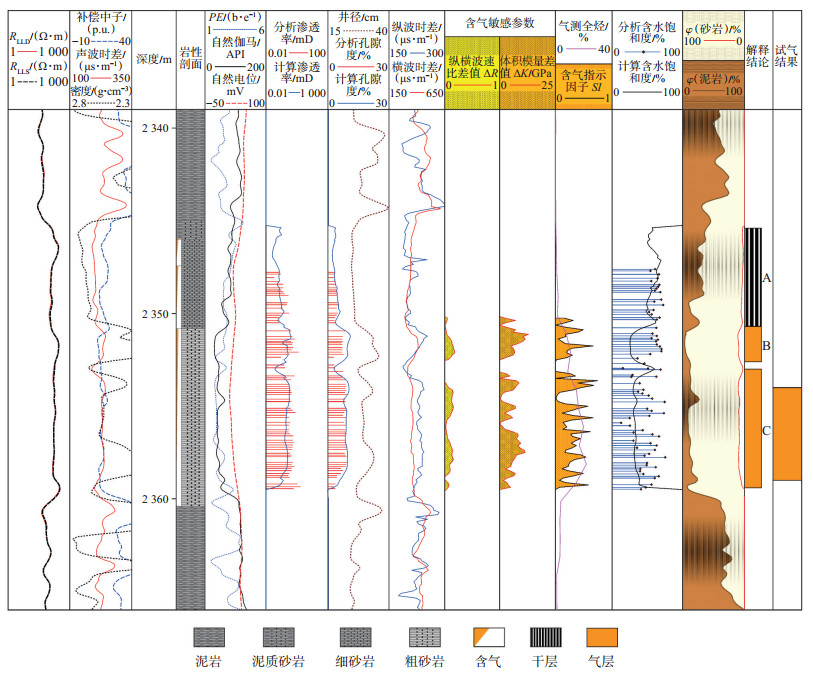
|
下载原图 图 3 鄂尔多斯盆地东部致密砂岩储层X井2 340~ 2 365 m段致密砂岩储层含气性评价成果图 Fig. 3 Gas-bearing property evaluation results of tight sandstone reservoir at 2 340-2 365 m of well X in eastern Ordos Basin |
图 4为研究区Y井2 530~2 570 m段致密砂岩储层含气性评价成果图。在气层A段和C段,ΔK>0,SI>0,能够很好地识别致密砂岩储层的含气性,而纵横波速度比差值ΔR仅在部分井段显示大于0,识别效果较差;在干层B段,ΔK<0,ΔR<0,SI<0,同样表明该井段不含天然气。其中,该井段A段与C段孔隙度分别为9.41%和9.68%,渗透率分别为0.691 mD和0.401 mD,含气饱和度分别为55.50%和59.47%,综合解释为气层。经生产测试验证,该井分层合试,压裂后试气日产气为5.267 7万m3/d,解释结论与试气结果一致。
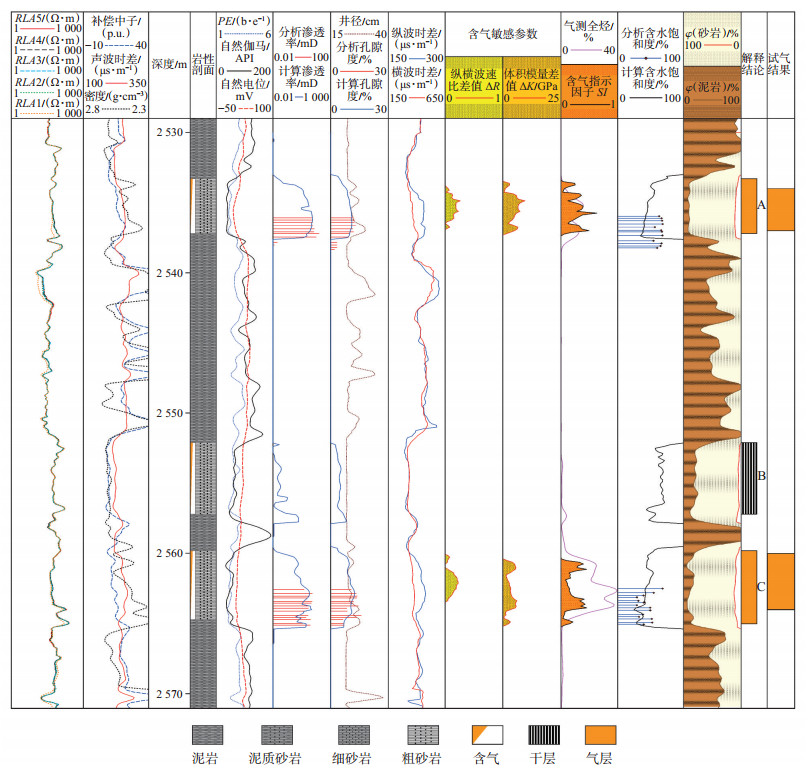
|
下载原图 图 4 鄂尔多斯盆地东部致密砂岩储层Y井2 530~2 570 m段致密砂岩储层含气性评价成果图 Fig. 4 Gas-bearing property evaluation results of tight sandstone reservoir at 2 530-2 570 m of well Y in eastern Ordos Basin |
在储层含气性评价成果图中,X井2 353~2 354 m段(C段)和Y井2 564~2 565 m段(C段)的纵横波速度比差值识别指标与体积模量差值和含气指示因子识别指标不吻合,此时以含气敏感参数体积模量差值和含气指示因子作为最终的判别依据。
这些井的成功解释,进一步印证了基于Xu-White模型,利用阵列声波测井资料,结合Biot-Gassmann方程和流体替换模型构建的含气敏感参数体积模量差值和含气指示因子在鄂尔多斯盆地东部致密砂岩气层识别中具有良好的适用性,同时为其他地区同类致密砂岩储层的含气性评价提供了一定的技术支持。
4 结论(1)致密砂岩气藏地质条件复杂,储层储集和渗透性能差,流体识别困难,阵列声波测井能够提供反映地层真实骨架和流体特征的声学信息,是致密砂岩储层非电法测井含气性评价的有效手段。
(2)地层弹性模量对天然气的敏感性很高,基于Xu-White模型,通过Biot-Gassmann方程预测100%饱含水地层的体积模量与阵列声波测井资料获取的地层真实体积模量差值作为含气敏感参数指标,评价致密储层含气性的方法效果较好。
(3)基于Xu-White模型,利用阵列声波测井资料提取的纵、横波速度数据,结合Biot-Gassmann方程和流体替换模型构建含气指示因子的方法,有效地评价了致密砂岩储层的含气性,通过生产测试资料验证,该方法识别气层准确度较高,在鄂尔多斯盆地东部致密砂岩气层含气性评价中应用效果良好。
| [1] |
董瑞霞, 范晓敏. 致密砂岩气层综合识别方法的改进. 世界地质, 2003, 22(3): 266-270. DONG R X, FAN X M. Improvement of method for distinguishing formation containing gas from compact sandstone. Global Geology, 2003, 22(3): 266-270. |
| [2] |
柳娜, 周兆华, 任大忠, 等. 致密砂岩气藏可动流体分布特征及其控制因素:以苏里格气田西区盒8段与山1段为例. 岩性油气藏, 2019, 31(6): 14-25. LIU N, ZHOU Z H, REN D Z, et al. Distribution characteristics and controlling factors of movable fluid in tight sandstone gas reservoir:a case study of the eighth member of Xiashihezi Formation and the first member of Shanxi Formation in western Sulige Gas Field. Lithologic Reservoirs, 2019, 31(6): 14-25. |
| [3] |
中国石油勘探与生产分公司. 低孔低渗油气藏测井评价技术及应用. 北京: 石油工业出版社, 2009. PetroChina Exploration & Production Company. Evaluation technology and application of well logging in low-porosity and lowpermeability oil and gas reservoirs. Beijing: Petroleum Industry Press, 2009. |
| [4] |
楚翠金, 夏志林, 杨志强. 延川南区块致密砂岩气测井识别与评价技术. 岩性油气藏, 2017, 29(2): 131-138. CHU C J, XIA Z L, YANG Z Q. Logging identification and evaluation of tight sandstone gas in the southern Yanchuan block. Lithologic Reservoirs, 2017, 29(2): 131-138. |
| [5] |
范宜仁, 邢东辉, 邓少贵, 等. 低渗透岩石声学特征及在含气性预测中的应用. 西南石油大学学报(自然科学版), 2015, 37(5): 64-70. FAN Y R, XING D H, DENG S G, et al. Acoustic properties of low permeability cores and its application to reservoir gas predication. Journal of Southwest Petroleum University(Science & Technology Edition), 2015, 37(5): 64-70. |
| [6] |
张永军, 顾定娜, 马肃滨, 等. 阵列声波测井资料在吐哈油田致密砂岩气层识别中的应用. 测井技术, 2012, 36(2): 175-178. ZHANG Y J, GU D N, MA S B, et al. The application of array acoustic wave data to tight sandstone gas reservoir in Tuha Oilfield. Well Logging Technology, 2012, 36(2): 175-178. |
| [7] |
张海涛, 石玉江, 张鹏, 等. 基于偶极横波测井的低渗透砂岩气层识别方法. 测井技术, 2015, 39(5): 591-595. ZHANG H T, SHI Y J, ZHANG P, et al. The identification of low permeability sandstone gas reservoir based on the DSI. Well Logging Technology, 2015, 39(5): 591-595. |
| [8] |
成志刚, 张蕾, 赵建武, 等. 利用岩石声学特性评价致密砂岩储层含气性. 测井技术, 2013, 37(3): 253-257. CHENG Z G, ZHANG L, ZHAO J W, et al. Gas evaluation in tight sand reservoir using acoustic characteristic of rock. Well Logging Technology, 2013, 37(3): 253-257. |
| [9] |
陈国文, 邓志文, 姜太亮, 等. 纵横波联合解释技术在气云区的应用. 岩性油气藏, 2019, 31(6): 79-87. CHEN G W, DENG Z W, JIANG T L, et al. Application of PPwave and SS-wave joint interpretation technology in gas cloud area. Lithologic Reservoirs, 2019, 31(6): 79-87. |
| [10] |
HASHIN Z, SHTRIKMAN S. A variational approach to the theory of the elastic behavior of multiphase materials. Journal of the Mechanics and Physics of Solids, 1963, 11(2): 127-140. DOI:10.1016/0022-5096(63)90060-7 |
| [11] |
BERRYMAN J G. Mixture theories for rock properties//Thomas J A. Rock physics and phase relations: a handbook of physical constants. Washington DC: American Geophysical Union, 1995: 205-228.
|
| [12] |
MAVKO G, MUKERJI T, DVORKIN J. The rock physics handbook(Tools for seismic analysis of porous media) Ⅱ. New York: Cambridge University Press, 2009: 110-115.
|
| [13] |
HILL R. The elastic behavior of crystalline aggregate. Proceedings of the Physical Society, 1952, 65(5): 349-354. DOI:10.1088/0370-1298/65/5/307 |
| [14] |
BIOT M A. Theory of propagation of elastic waves in a fluid-saturated porous solid. Ⅰ. Low-frequency range. Journal of Acoustical Society of America, 1956, 28(2): 168. DOI:10.1121/1.1908239 |
| [15] |
GASSMANN F. Elastic waves through a packing of spheres. Geophysics, 1951, 16(4): 673-685. |
| [16] |
XU S Y, WHITE R E. A new velocity model for clay-sand mixtures. Geophysical Prospecting, 1995, 43(1): 91-118. DOI:10.1111/j.1365-2478.1995.tb00126.x |
| [17] |
XU S Y, WHITE R E. A physical model for shear-wave velocity prediction. Geophysical Prospecting, 1996, 44(4): 687-717. DOI:10.1111/j.1365-2478.1996.tb00170.x |
| [18] |
KUSTER G T, TOKSOZ M N. Velocity and attenuation of seismic waves in two-phase media. Geophysics, 1974, 39(5): 587-618. DOI:10.1190/1.1440450 |
| [19] |
彭达, 肖富森, 冉崎, 等. 基于KT模型流体替换的岩石物理参数反演方法. 岩性油气藏, 2018, 30(5): 82-90. PENG D, XIAO F S, RAN Q, et al. Inversion of rock physics parameters based on KT model fluid substitution. Lithologic Reservoirs, 2018, 30(5): 82-90. |
| [20] |
ESHELBY J D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proceedings of the Royal Society a Mathematical Physical and Engineering Sciences, 1957, 241(1226): 376-396. |
| [21] |
WU T T. The effect of inclusion shape on the elastic moduli of a two-phase material. International Journal of Solids and Structures, 1966, 2(1): 1-8. DOI:10.1016/0020-7683(66)90002-3 |
| [22] |
KEY R G, XU S Y. An approximation for the Xu-White velocity model. Geophysics, 2002, 67(5): 1406-1414. DOI:10.1190/1.1512786 |
| [23] |
WOOD A W. A textbook of sound. New York: The MacMillam Company, 1955: 360.
|
| [24] |
BRIE A, PAMPURI F, MARSALA A F, et al. Shear sonic interpretation in gas-bearing sands. SPE 30595, 1995. |
 2020, Vol. 32
2020, Vol. 32



