0 引言

利用地表观测的地球物理资料来推断地下介质物理参数是一个地球物理反演问题。地震反演通过结合地震、测井、钻井资料及已知的地质规律来估计储层弹性参数，对岩性预测和流体识别具有重要的指导意义。常规的确定性反演只能提供一个最优解^[1-3]，无法对模型参数进行不确定性分析。而概率统计反演方法将反演结果以概率的形式表示，可以获得模型参数的多次实现，能够对反演结果进行不确定性分析。因此，概率统计反演在一定程度上可以避免反演结果不确定性导致的预测风险。概率统计反演分为贝叶斯反演和地质统计学反演两类方法。

在贝叶斯反演中，将模型参数的解表示为后验概论密度函数^[4-6]。后验概率密度函数的解析解通常无法求取，可利用马尔科夫蒙特卡洛（Markov chain Monte Carlo，McMC）方法进行抽样求解^[7-8]。张广智等^[9]将该算法应用于叠前地震反演，获得了纵横波阻抗和密度反射系数。王辉等^[10]利用该算法在叠前域反演了纵横波速度和密度。但对于高斯线性假设，即模型参数的先验概率密度函数是高斯分布并且正演算子可以线性化，则可以获得后验概率密度函数的解析解^[5]。Buland等^[11]通过线性高斯假设并利用叠前地震资料进行纵横波速度和密度参数反演。滕龙等^[12]通过线性高斯假设进行弹性参数与物性参数的联合反演。为表征离散岩性和流体对模型参数的分布影响，Grana等^[13-14]将模型参数的先验分布表示为混合高斯分布，通过线性假设得到混合高斯线性反演解。

在地质统计学反演中，通过序贯模拟或非序贯模拟算法来构建模型参数的先验信息，然后不断扰动模型参数来匹配观测数据，从而得到模型参数反演解，这种方法通常计算量非常大，且不能保证反演解收敛。Bortoli等^[15]和Haas等^[16]最早将序贯高斯模拟算法应用于地质统计学反演。余振等^[17]利用序贯高斯模拟和序贯指示模拟算法进行地质统计学反演，并实现了高分辨率的流体预测。由于序贯高斯模拟通常须要对模型参数进行正态变换，Soares等^[18]、Caetano等^[19]、Azevedo等^[20]利用直接序贯模拟算法进行地震随机反演。为快速构建模型参数的先验信息，孙瑞莹等^[21]、王保丽等^[22]、Yang等^[23]利用非序贯模拟的FFT-MA谱模拟算法进行随机反演。针对两点地质统计学的不足，González等^[24]和刘兴业等^[25]利用多点地质统计学进行地震随机反演。由于传统的序贯模拟算法通过求解克里金方程组来获得待模拟点的均值和方差^[26-29]，再利用蒙特卡洛的方法逐点随机模拟该点的值。当克里金方程组较大时，求解过程非常耗时。因此，Hansen等^[30]将线性高斯理论与序贯模拟相结合来求取待模拟点的后验均值和方差，避免求解大型协方差矩阵和扰动优化过程，直接获得模型参数的多次实现，但是该方法没有考虑离散岩性和流体对模型参数的先验分布影响，只能单一地反演连续变量的模型参数。

在Hansen等^[30]的研究基础上，将模型参数的先验分布表示为受离散岩性影响的混合高斯分布，并将线性混合高斯理论与序贯模拟相结合，同时获得声波阻抗与岩性的多次实现，以期反演结果具有较好的空间连续性和稳定性。

1 序贯模拟的线性混合高斯反演 1.1 混合高斯先验分布

由于离散岩性的影响，模型参数如弹性阻抗、孔隙度、含水饱和度等连续变量呈现多峰的混合高斯分布。模型参数服从多峰的混合高斯概率密度函数，可以表示为

$ m \sim \sum\nolimits_{l=1}^{L} p_{l} N\left(m ; \mu_{m}^{l}, \sum\nolimits_{m}^{l}\right) $

(1)

式中：L为高斯分量的个数，这里表示离散岩性的个数；p_l为第l个高斯分量的先验权值；$ N\left(m ; \mu_{m}^{l}, \sum_{m}^{l}\right)$为混合高斯的第l个高斯分量，表示为

$ N\left(m ; \mu_{m}^{l}, \sum\nolimits_{m}^{l}\right)=\frac{1}{(2 {\rm{ \mathsf{ π}}})^{\frac{n}{2}}} \frac{1}{\left|\sum\nolimits_{m}^{l}\right|^{\frac{1}{2}}} \cdot \exp \left[-\frac{1}{2}\left(m-\mu_{M}^{l}\right)^{T}\left(\sum\nolimits_{m}^{l}\right)^{-1}\left(m-\mu_{m}^{l}\right)\right] $

(2)

式中：μ_m^l和$ \sum_{m}^{l}$分别为第l个分量的先验均值和协方差矩阵，l = 1，2，…，L；T表示转置。

1.2 混合高斯线性反演解

假设观测数据d和模型参数m之间的正演关系可以用线性算子G表示，即d = Gm + ε，地震噪声ε服从高斯分布。如果模型参数m的先验信息服从混合高斯分布，那么模型参数m的后验条件分布也服从混合高斯分布^[13-14]，如下：

$ m \mid d \sim \sum\nolimits_{l=1}^{L} q_{m \mid d}^{l} N\left(m ; \mu_{m \mid d}^{l}, \sum\nolimits_{m \mid d}^{l}\right) $

(3)

式中：μ_m|d^l和$ \sum_{m \mid d}^{l} $分别为第l个分量的后验条件均值、协方差矩阵：

$ \mu_{m \mid d}^{l}=\mu_{m}^{l}+\sum\nolimits_{m}^{l} G^{T}\left(K_{m, \varepsilon}\right)-1\left(d-G \mu_{m}^{l}\right) $

(4)

$ \sum\nolimits_{m \mid d}^{l}=\sum\nolimits_{m}^{l}-\sum\nolimits_{m}^{l} G^{T}\left(K_{m, e}\right)^{-1} G \sum\nolimits_{m}^{l} $

(5)

式中：$ K_{m, \varepsilon}=G \sum_{m}^{l} G^{T}+\sum_{\varepsilon}, q_{m \mid d}^{l}$代表后验条件系数：

$ q_{m \mid d}^{l}=\frac{p_{l} N\left(d ; \mu_{d}^{l}, \sum\nolimits_{d}^{l}\right)}{\sum\limits_{i=1}^{L} p_{i} N\left(d ; \mu_{d}^{i}, \sum\nolimits_{d}^{i}\right)} $

(6)

式中：$ \mu_{d}^{i}=G \mu_{m}^{i}, \sum_{d}^{i}=\sum_{m}^{i} G^{T}+\sum_{\varepsilon}$。

1.3 线性混合高斯序贯采样

为了提高反演解的精度和稳定性，将低频模型d_f作为待采样点的条件数据，低频模型可以通过井插值或者其他方法获取。低频模型可以表示为^[31]：

$ d_{\mathrm{f}}=m+\varepsilon_{\mathrm{f}} $

(7)

式中：ε_f是一个协方差为$ \sum_{\mathrm{f}}$的噪声，描述了反演结果与模型参数的相似度。

将d = G m + ε和式（7）联合可以写成：

$ \left[\begin{array}{l} d \\ d_{\mathrm{f}} \end{array}\right]=\left[\begin{array}{l} G \\ E \end{array}\right] m+\left[\begin{array}{l} \varepsilon \\ \varepsilon_{\mathrm{f}} \end{array}\right] $

(8)

式中：E表示单位矩阵。

如果$d^{\prime}=\left[\begin{array}{c}d \\ d_{\mathrm{f}}\end{array}\right], G^{\prime}=\left[\begin{array}{l}G \\ E\end{array}\right], \varepsilon^{\prime}=\left[\begin{array}{l}\varepsilon \\ \varepsilon_{\mathrm{f}}\end{array}\right] $，则式（8）可以写成：

$ d^{\prime}=G^{\prime} m+\varepsilon^{\prime} $

(9)

根据Hansen等^[30]提出的线性高斯序贯采样理论，在线性混合高斯序贯采样过程中，须要估算待采样点m_x在三类条件数据（m_k，d及d_f）下的后验条件分布，这里的m_k表示已采样点的模型参数自身。该后验条件分布m_x| (m_k, d, d_f)也服从混合高斯分布，即m_x| (m_k, d^')服从混合高斯分布：

$ {m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right) \sim \sum\limits_{l = 1}^L {q_{GMM}^l} N\left[ {m;\mu _{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l, \sum\nolimits_{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l {} } \right]} \right. $

(10)

其均值和协方差分别变为：

$ \begin{array}{c} \mu _{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l = {A_x}m_m^l + \left[ {{A_x}\sum\nolimits_m^l {A_{\rm{k}}^T} {A_x}\sum\nolimits_m^l {{G^{\prime T}}} } \right] \cdot \\ {\left( {\sum\nolimits_{\left( {{m_{\rm{k}}}, {d^\prime }} \right)}^l {} } \right)^{ - 1}}\left[ {\begin{array}{*{20}{l}} {{m_{\rm{k}}} - {A_{\rm{k}}}\mu _m^l}\\ {{d^\prime } - {G^{\prime T}}\mu _m^l} \end{array}} \right] \end{array} $

(11)

$ \begin{array}{c} \sum\nolimits_{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l {} = {A_x}\sum\nolimits_m^l {A_x^T} - \left[ {{A_x}\sum\nolimits_m^l {A_{\rm{k}}^T} {A_x}\sum\nolimits_m^l {{G^T}} } \right] \cdot \\ {\left[ {\sum\nolimits_{\left( {{m_{\rm{k}}}, {d^\prime }} \right)}^l {} } \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{A_{\rm{k}}}\sum\nolimits_m^l {A_x^T} }\\ {{G^\prime }\sum\nolimits_m^l {A_x^T} } \end{array}} \right] \end{array} $

(12)

式中：$ \sum\nolimits_{\left( {{m_{\rm{k}}}, {d^\prime }} \right)}^l = \left[ {\begin{array}{*{20}{c}} {{A_{\rm{k}}}\sum\nolimits_m^l {A_x^T} }&{{A_{\rm{k}}}\sum\nolimits_m^l {{G^{\prime T}}} }\\ {{G^\prime }\sum\nolimits_m^l {A_{\rm{k}}^T} }&{{G^\prime }\sum\nolimits_m^l {{G^{\prime T}}} + \sum\nolimits_\varepsilon {} } \end{array}} \right]$，A_x和A_k分别表示将待采样点m_x和已知点m_k从模型参数m中提取出来的矩阵，则m_x和m_k分别可以成m_x = A_x m_k = A_k m。

后验条件权值变为：

$ q_{{\rm{GMM}}}^l = \frac{{{p_l}N\left\{ {\left[ {\begin{array}{*{20}{l}} {{m_{\rm{k}}}}\\ {{d^\prime }} \end{array}} \right];\left[ {\begin{array}{*{20}{l}} {{A_{\rm{k}}}\mu _m^l}\\ {{G^\prime }\mu _m^l} \end{array}} \right]\sum\nolimits_{\left( {{m_{\rm{k}}}d} \right)}^l {} } \right\}}}{{\sum\nolimits_{i = 1}^L {{p_i}} N\left\{ {\left[ {\begin{array}{*{20}{l}} {{m_{\rm{k}}}}\\ {{d^\prime }} \end{array}} \right];\left[ {\begin{array}{*{20}{l}} {{A_{\rm{k}}}\mu _m^i}\\ {{G^\prime }\mu _m^i} \end{array}} \right] \cdot \sum\nolimits_{\left( {{m_{\rm{k}}}d} \right)}^l {} } \right\}}} $

(13)

线性混合高斯序贯采样的步骤如下：

（1）定义模拟网格，利用随机种子随机访问模拟网格中的待采样点m_x。

（2）利用式（11）—（13）分别计算待采样点的后验条件均值$\mu _{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l $、协方差$\sum\nolimits_{{m_x}\left| {\left( {{m_{\rm{k}}}, {d^\prime }} \right)} \right.}^l {} $以及后验条件权值q_GMM^l。

（3）比较后验条件权值系数确定待采样点的离散岩性，即高斯分量，然后从确定的高斯分量中随机抽取一个值，作为当前待采样点的连续变量的模型参数值。

（4）随机访问下一个待采样点，并将上一次采样点的值作为该点的条件数据。

（5）重复步骤（1）—（4），直到访问完所有采样点。这种逐点序贯采样的方法，在反演每一个点的时候，由于考虑了模型参数、观测数据及低频模型等多类条件数据，实际上是对空间相关的后验分布进行采样，使得反演结果具有较好的空间连续性。通过选取合理的反演时窗和模拟邻域，可以避免大型协方差矩阵的计算，从而提高计算效率。

2 模型测试

为验证本文提出的方法的有效性，这里利用二维模型来验证本文提出方法的有效性。

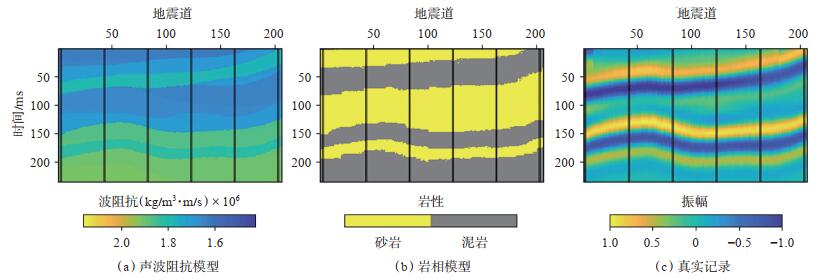
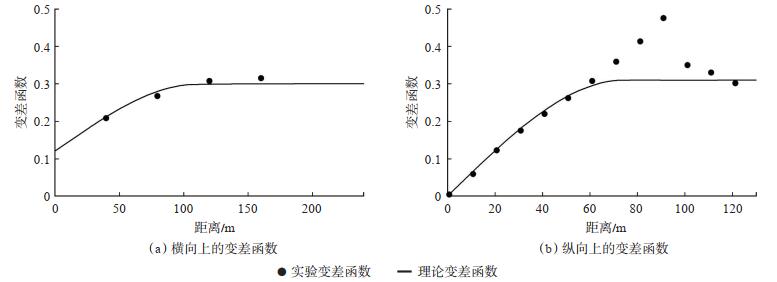
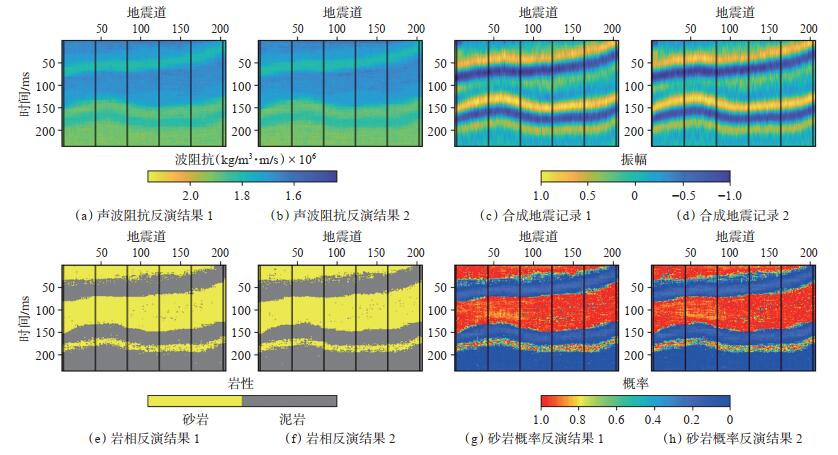
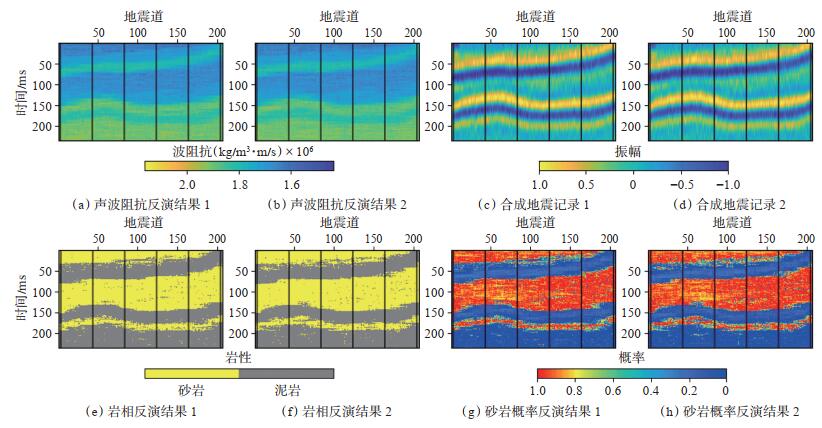
图 1（a）是声波阻抗模型，图 1（b）是岩相模型，图 1（c）是真实记录，一共206道，每道302个采样点，并假设每个网格大小为1 m×1 m。模型中的黑线表示抽取的伪井，伪井可以用来求取协方差矩阵，并在反演过程中充当条件数据。图 2是从抽取的伪井中统计的变差函数，利用球状理论变差函数来拟合实验变差函数，声波阻抗在横向上的变程为110 m，纵向上的变程为75 m。利用变差函数与协方差函数的关系：γ（h）= 1 - C（h），可以求取声波阻抗的空间协方差。首先进行无噪测试，反演结果如图 3所示。可以看到，反演的两次声波阻抗、岩性及合成记录与模型数据吻合较好。其中2次岩性反演结果的归类正确率分别为93.63% 和93.53%。图 3（g）和图 3（h）是2次反演的砂岩概率，可以用于岩性的不确定性分析，然后进行信噪比为4的加噪测试，反演结果如图 4所示。可以看到，2次的反演结果与合成记录的精度较图 3有所下降，但仍然与模型数据能够较好地吻合。其中，2次岩性反演结果的归类正确率分别为92.18% 和92.24%。图 4中砂岩概率的2次反演结果较图 3的结果出现了一定的波动性，这是加入的噪声所引起的，但这并没有对岩性的归类结果产生大的影响。

3 实际应用

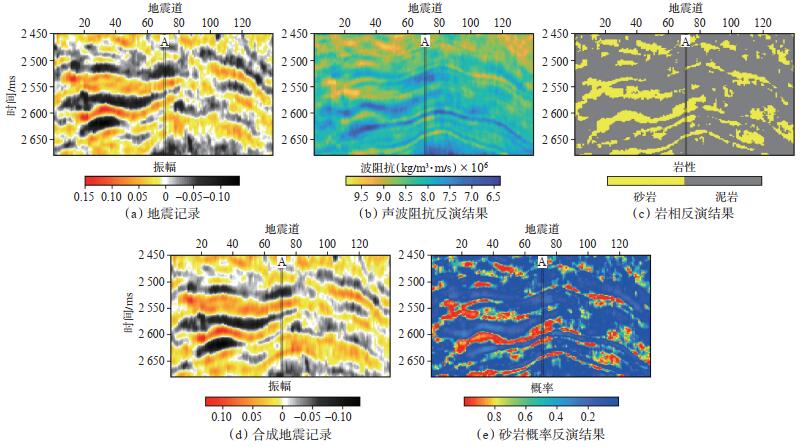
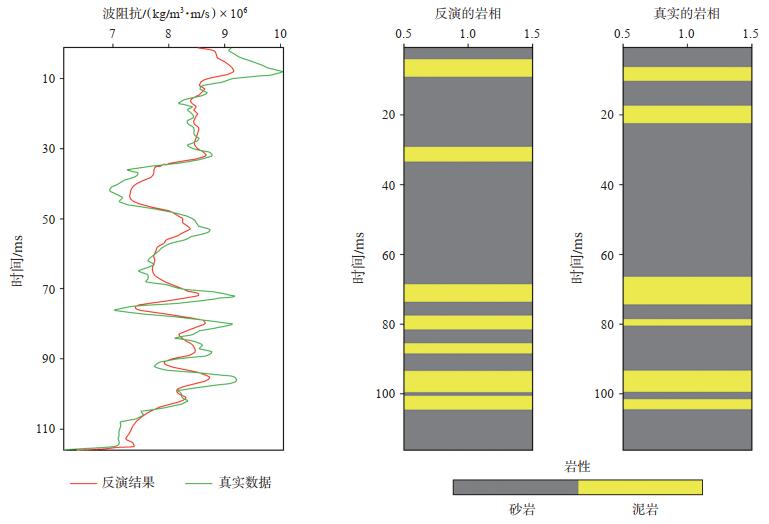
为了验证该方法的实际效果，以国内东部某油田的工区资料进行了应用。该工区以砂泥岩为主，且砂岩的阻抗较高，泥岩的阻抗较低。图 5（a）为原始的二维叠后地震记录，共有139道，反演时窗为2 450~2 680 ms，采样率为2 ms，其中A井用作验证井。图 5（b）和图 5（c）分别是声波阻抗和岩性的反演结果，可看到反演结果具有较好的横向展布，将反演的声波阻抗与子波合成的地震记录如图 5（d）所示，与真实的地震记录吻合较好。图 5（e）是砂岩概率的反演结果，可以预测有利储层的位置。为了验证本文提出的方法的可靠性，将A井位置处抽取的反演结果和A井数据对比，如图 6所示，可以看到声波阻抗吻合较好，岩性结果除了少数点被错误归类外，大部分与真实岩性吻合较好，归类正确率达82.76%。

4 结论

（1）混合高斯模型能够表征模型参数的多峰分布，将其与地质统计学的序贯模拟相结合可以同时反演连续变量和离散岩性。相比传统的地质统计学反演，这种方法在序贯采样的过程中，同时考虑了模型参数自身、观测数据及低频模型，属于边模拟边反演的过程，而不是先模拟再反演的过程。

（2）低频模型的加入能让反演结果更加稳定，不易受噪声的影响，空间相关的后验序贯采样使得反演结果具有较好地空间连续性。这种方法还可以用于弹性阻抗反演、叠前AVO反演。

（3）需要指出的是，这种边模拟边反演的方法由于直接以地震数据作为条件数据，缺少了模型参数的小尺度变化性，使得这种方法的垂向分辨率受到一定的影响。