2. 长江大学 地球物理与石油资源学院, 武汉 430100;
3. 长江大学 录井技术与工程研究院, 湖北 荆州 434023
2. School of Geophysics and Oil Resources, Yangtze University, Wuhan 430100, China;
3. Institute of Mud Logging Technology and Engineering, Yangtze University, Jingzhou 434023, Hubei, China
因地层吸收作用,地震波在地下介质传播中会发生振幅衰减和相位畸变,从而主频降低,频带变窄,地震资料的分辨率降低[1-4]。反Q滤波[5-7]、Gabor反褶积[8-9]和Q偏移[10-11]等方法通常被用来进行地震波的衰减补偿,以提高地震资料的分辨率。就反Q滤波而言,由于硬件存储精度的限制,为解决反Q滤波振幅补偿会出现的数值稳定性问题[5],学者们提出了一些稳定的反Q滤波方法,如稳定因子法、迭代法、正则化法[5, 12-13]、反演方法[14]、频域[15-16][3]方法[17]等。这些方法的振幅补偿函数是固定的,对于任何地震记录,其振幅补偿强度和频带补偿宽度均相同,但地震记录是非平稳信号,其振幅能量分布和有效频带范围都是随时间或深度变化而变化的。当地震记录含有噪声时,常规稳定的反Q滤波方法无法结合地震记录有效频带范围对其进行差别补偿,导致其在某些时刻会同时增强有效振幅和噪声能量,影响反Q滤波后地震记录的信噪比。Zhao等[18]结合地震记录的非平稳性,提出一种时频域信噪比的估算方法,并将其用于稳定因子法反Q滤波,该方法基于时频域信噪比估算的有效频带范围,所以只在有效频带范围内进行稳定的反Q滤波补偿,在一定程度上压制了噪声能量,但该方法振幅补偿函数的增益限未与有效频带范围相结合,对某些时刻的振幅能量也存在一定的压制。张固澜等[19]提出一种稳定的自适应增益限反Q滤波方法,其考虑了地震记录的有效频带宽度,并使增益限和稳定因子自适应于有效频带的截止频率,同时指出可通过分析地震资料的频谱来获取有效频带的截止频率。
在自适应增益限反Q滤波的基础上,结合时频域信噪比的概念,提出一种基于时频域信噪比的自适应增益限反Q滤波方法。首先,从地震记录相邻地震道中提取信号和噪声统计量,以多道平均的方式估算地震记录的时频域信噪比;然后,根据信噪比阈值确定有效频带截止频率;最后,结合自适应于截止频率的增益限反Q滤波方法对地震记录进行时变增益振幅补偿。
1 基本原理 1.1 稳定的反Q滤波方法反Q滤波以一维波动方程[5]为基础
| $ \frac{{{\partial ^{\rm{2}}}U\left( {z, \omega } \right)}}{{\partial {z^{\rm{2}}}}} + {k^{\rm{2}}}U(z, \omega ) = {\rm{0}} $ | (1) |
式(1)中:U (z, ω) 为传播距离为z时角频率为ω的平面波;k为波数,
| $ U(\tau + \Delta \tau ,\omega ) = U(\tau ,\omega ){\rm{exp}}\left[ { - i{{(\frac{\omega }{{{\omega _{\rm{h}}}}})}^{ - \gamma }}\omega \Delta \tau } \right]{\rm{exp}}( - \frac{{\omega \Delta \tau }}{{{\rm{2}}Q}}) $ | (2) |
式(2)中:τ为传播时间;Δτ为时间间隔;U (τ + Δτ, ω)和U (τ, ω) 分别是τ + Δτ和τ时刻的波场;
| $ U(\tau + \Delta \tau , \omega ) = U(\tau , \omega ){\rm{exp}}\left[ {i{{(\frac{\omega }{{{\omega _{\rm{h}}}}})}^{ - \gamma }}\omega \Delta \tau } \right]{\rm{exp}}(\frac{{\omega \Delta \tau }}{{{\rm{2}}Q}}) $ | (3) |
由于地震波衰减到一定程度时,环境噪声的能量会高于信号能量,因此,反Q滤波会对环境噪声进行放大,造成数值不稳定。这种不稳定主要是由式(3)中的振幅校正算子
| $ U(\tau , \omega ) = \tilde U(t, \omega )\Theta (t, \omega )\frac{{{A^{ - {\rm{1}}}}(t, \omega ) + {c^{\rm{2}}}}}{{{A^{ - {\rm{2}}}}(t, \omega ) + {c^{\rm{2}}}}} $ | (4) |
式(4)中:
自适应增益限反Q滤波方法[19]由以下公式实现
| $ U(t,\omega ) = \left\{ {\begin{array}{*{20}{l}} {\tilde U(t,\omega )A(t,\omega )}&{\omega \le {\omega _{\rm{d}}}(t)}\\ {2\tilde U(t,\omega )\Theta (t,\omega )\frac{{{A^{ - {\rm{1}}}}(t,\omega ) + {{[{c^{\rm{2}}}(t) - {\rm{2}}c(t)]}^{ - {\rm{1}}}}}}{{{A^{ - {\rm{2}}}}(t,\omega ) + {{[{c^{\rm{2}}}(t) - {\rm{2}}c(t)]}^{ - {\rm{1}}}}}}}&{\omega > {\omega _{\rm{d}}}(t)} \end{array}} \right. $ | (5) |
式(5)中:t为旅行时;ωd (t) 为有效频范围的截止角频率;A(t, ω) 是振幅补偿函数;c(t) 是振幅补偿函数U (t, ω) 的时变增益限,dB;其与地震波有效频范围的截止角频率相对应;[c2 (t)-2c (t)]-1是稳定因子,主要用于压制高频噪声和吉布斯效应,以解决反Q滤波的非稳定性问题;
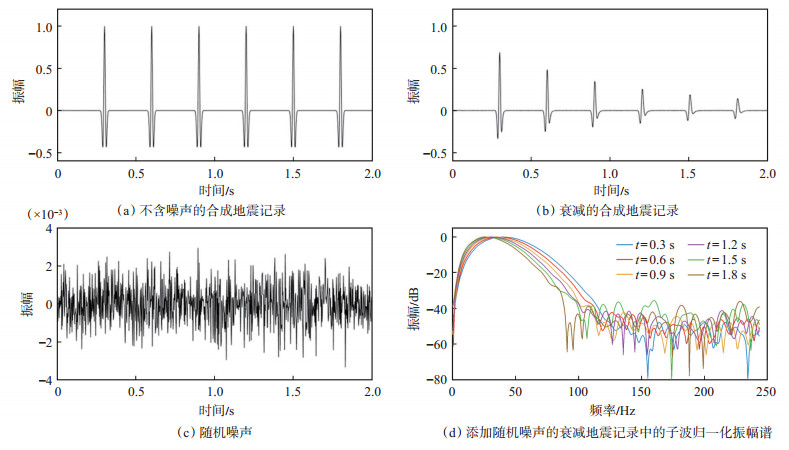
为了验证自适应增益限反Q滤波的有效性,分别利用常规稳定的反Q滤波方法和自适应增益限反Q滤波方法对含噪声合成地震记录进行振幅补偿。图 1(a)为不含噪声的合成地震记录,子波主频为35 Hz,采样间隔为2 ms。图 1(b)为对图 1(a)中的记录进行Q =100的衰减模拟结果,可以看到,随着旅行时的增加,子波振幅逐渐衰减,相位畸变,波形产生变化。图 1(c)为均值为0的随机噪声,其标准差为图 1(a)中记录的最大幅度的0.1%。将图 1(c)中的随机噪声添加到图 1(b)中的衰减地震记录中,得到含有噪声的衰减合成地震记录,分别在0.3 s,0.6 s,0.9 s,1.2 s,1.5 s和1.8 s处提取子波,计算其归一化对数振幅谱[图 1(d)],可以看到,随着旅行时的增加,子波振幅谱的高频成分逐渐减少,有效振幅频带逐渐“变窄”。
|
下载原图 图 1 合成地震记录 Fig. 1 Synthetic seismic records |
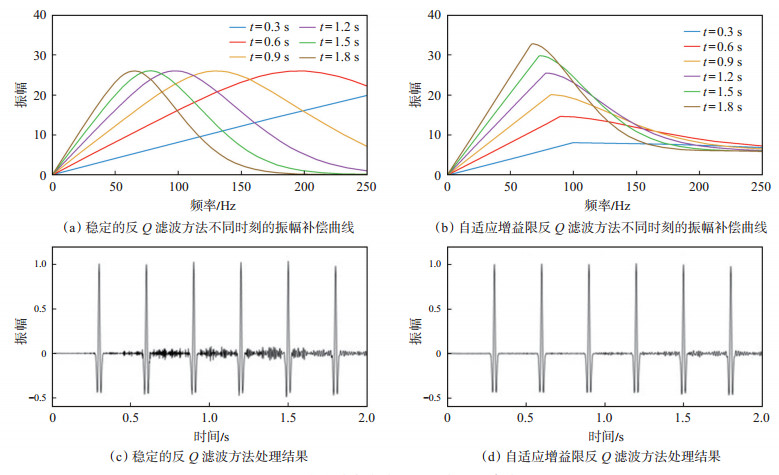
图 2(a)为t =0.3 s,0.6 s,0.9 s,1.2 s,1.5 s,1.8 s时稳定的反Q滤波振幅补偿曲线,增益限为20 dB,可以看到,虽然不同时刻的振幅补偿频带范围不同,但是其振幅补偿曲线的最大值是相同的。图 2(b)为t =0.3 s,0.6 s,0.9 s,1.2 s,1.5 s,1.8 s时自适应增益限的反Q滤波振幅补偿曲线,其增益限随着有效频带截止频率的变化而变化。从图 1(d)中可以读出上述6个时刻的截止角频率ωd分别为200π,180 π,164 π,156π,146 π和134 π,由图 2(b)可看到,不同时刻的振幅补偿频带范围不同,而且其振幅补偿曲线的最大值也是不同的,这体现了自适应增益限反Q滤波的优势所在。分别用稳定的反Q滤波和自适应增益限反Q滤波方法对图 1中的含噪声衰减记录进行反Q滤波,其结果分别如图 2(c)和图 2(d)所示。可以看到,稳定的反Q滤波方法可补偿子波的振幅能量,但也对噪声能量进行了放大,而自适应增益限反Q滤波方法既补偿了子波的振幅能量,同时也压制了大部分随机噪声能量。
|
下载原图 图 2 图 1中衰减合成地震记录的反Q滤波结果 Fig. 2 Inverse Q filtering results of the attenuated synthetic seismic records in Fig. 1 |
由式(5)可知,自适应增益限反Q滤波的振幅补偿结果依赖于地震记录的有效频带范围,即有效频带的截止角频率ωd (t)。因此,本次研究将时频域信噪比的概念和自适应增益限反Q滤波方法结合起来,提出一种基于时频域信噪比的自适应增益限反Q滤波方法。该方法首先在相关理论的基础上从地震记录相邻地震道中提取信号和噪声的平均瞬时功率谱,并采用多道平均的方式估算地震记录的时频域信噪比[18]
| $ SNR(t, \omega ) = \frac{{{P_s}(t, \omega )}}{{{P_n}(t, \omega )}} = \frac{{{P_s}(t, \omega )}}{{{P_x}(t, \omega ) - {P_s}(t, \omega )}} $ | (6) |
式(6)中:Px (t, ω),Ps (t, ω) 和Pn (t, ω) 分别是地震道、信号和噪声的平均瞬时功率谱。
然后,根据地震记录的信噪比特征及地震数据处理的实际需求,选择阈值C0,并利用SNR (t, ω) ≥ C0计算地震记录随旅行时t变化的有效频带范围[ωa (t), ωb (t)]
| $ [{\omega _{\rm{a}}}(t), {\omega _{\rm{b}}}(t)] = \omega [SNR(t, \omega ) \ge {C_{\rm{0}}}] $ | (7) |
从式(7)可看出,该频带范围会随阈值C0的变化而变化,当C0变大时,有效频带“变窄”,反之,有效频带“变宽”。最后,确定反Q滤波中有效频带的截止角频率ωd (t)
| $ {\omega _{\rm{d}}}(t) = {\omega _{\rm{b}}}(t) $ | (8) |
并利用式(5)进行自适应增益限反Q滤波。
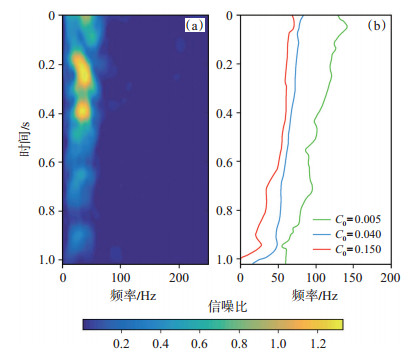
图 3中A为理论合成的不含衰减地震记录,共512个采样点,采样间隔为2 ms,在此作为参考道。B为对A中的地震记录进行Q =50的衰减模拟结果,同时添加随机噪声。C—E分别为阈值C0 =0.005,0.040和0.150情况下的基于时频域信噪比的自适应增益限反Q滤波结果。由图 3可以看到,不同的阈值C0,其反Q滤波结果具有明显差异。结合图 3和图 4可以看到,不同的阈值C0可得到不同的截止角频率ωd (t),进而得到不同的反Q滤波结果。以参考道为标准,当C0较小时,有效频带“过宽”,会出现过补偿,放大了噪声能量,如图 3中C所示;当C0较大时,有效频带“过窄”,深层地震记录振幅出现欠补偿,如图 3中E所示;当C0=0.04时,其反Q滤波结果最接近参考道,如图 3中D所示,此时阈值C0得到的有效频带截止频率较为合适。

|
下载原图 图 3 含噪声合成地震记录及不同阈值情况下的基于时频域信噪比的自适应增益限反Q滤波结果 Fig. 3 Noise-added synthetic seismic records and the re‐sults of self-adaptive gain-limit inverse Q filtering based on SNR in time-frequency domain under different thresholds |
|
下载原图 图 4 图 3中衰减地震记录B的时频域信噪比(a)及不同阈值情况下的有效频带截止频率曲线(b) Fig. 4 SNR in time-frequency domain of the attenuated seismic record B in Fig. 3 (a) and the cut-off frequency curves of effective band under different thresholds (b) |
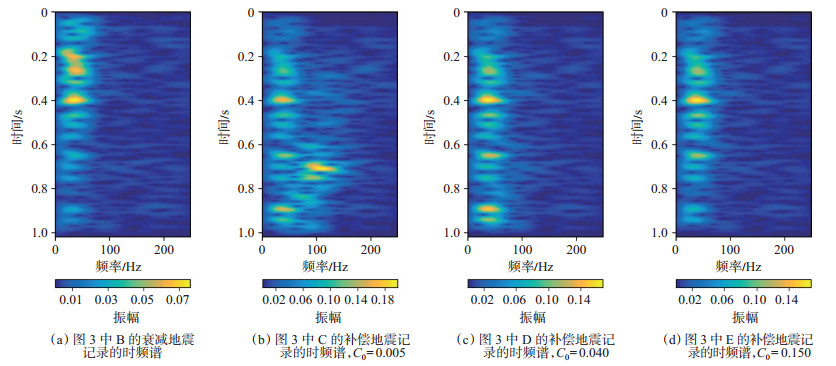
对于如何选取阈值C0,可以根据地震数据的时频域特征采用计算时频谱的方法定性分析,再结合图 3中的理论合成记录举例说明。计算图 3中B— E地震记录的时频谱(图 5)。由图 5(a)可看出,其浅层振幅能量较强,深层振幅能量较弱,噪声能量分布在整个频带范围内;由图 5(b)可看出,其深层出现异常强振幅能量,表现为高频噪声能量的增强;由图 5(c)可看出,补偿后的深层振幅能量与浅层基本一致,时频谱振幅能量比较均衡;把图 5(d)与图 5(a)相比,其深层振幅能量有所增强,但与图 5(c)相比,其振幅能量只得到部分补偿,表现为有效振幅能量相对较弱。由此可见,确定阈值C0 =0.04比较合适,对于实际地震数据,亦可采用上述方法优选合适的阈值。
|
下载原图 图 5 图 3中衰减地震记录在不同阈值情况下反Q滤波结果的时频谱 Fig. 5 Time-frequency spectra of the inverse Q filtering results of the attenuated seismic records in Fig. 3 under different thresholds |
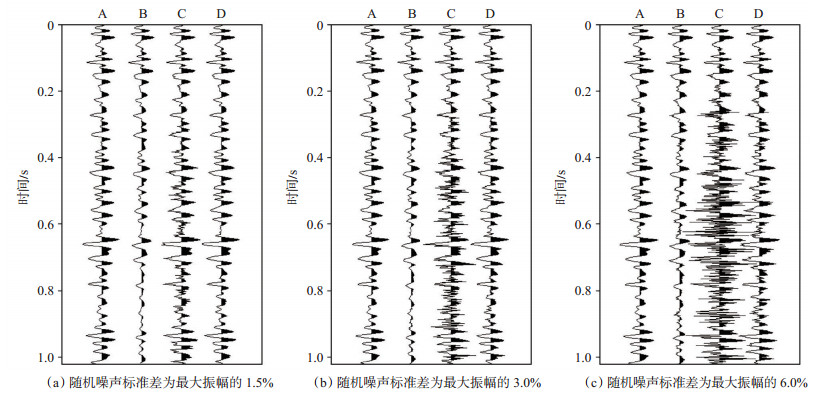
为进一步测试地震数据信噪比对研究方法的影响,采用3个不同信噪比的理论合成地震记录进行常规稳定的反Q滤波和基于时频域信噪比的自适应增益限反Q滤波,并对其结果进行对比分析(图 6)。图 6中的A为不含噪声的合成地震记录,共512个采样点,采样间隔为2 ms,在此作为参考道。对A中地震记录进行Q =100的衰减模拟,并分别添加标准差为A中地震记录最大幅度1.5%,3.0% 和6.0% 的随机噪声,分别如图 6中的B所示,可以看到,随着传播时间的增大,地震记录的有效振幅能量逐渐变弱,不同记录的噪声能量逐渐增强,信噪比逐渐降低。分别对3个不同信噪比的衰减地震记录进行常规稳定的反Q滤波,可以看到,随着信噪比的降低,常规稳定的反Q滤波对噪声能量的放大越来越明显,噪声能量越来越强,如图 6中的C所示。作为对比,分别对它们进行基于时频域信噪比的自适应增益限反Q滤波,如图 6中的D所示。由图 6可以看到,当原始衰减记录中的噪声能量较弱时,本文方法可以有效补偿振幅能量,并压制噪声能量,如图 6(a)和图 6(b)中的D所示。在噪声能量继续增强,信噪比继续降低的情况下,本文方法在补偿有效振幅能量的同时,亦会部分放大噪声能量,如图 6(c)中的D所示,但与常规稳定的反Q滤波结果相比,其对噪声能量的压制效果非常突出。
|
下载原图 图 6 基于时频域信噪比的自适应增益限反Q滤波 Fig. 6 Self-adaptive gain-limit inverse Q filtering based on SNR in time-frequency domain |
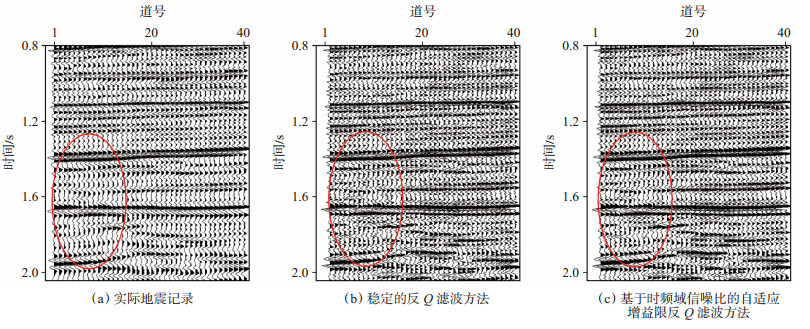
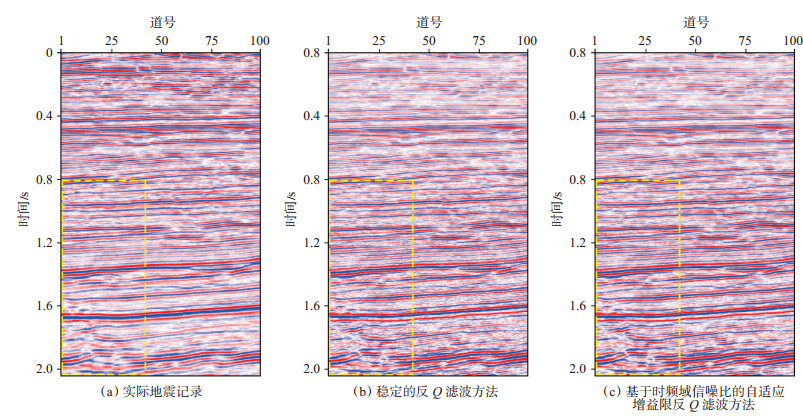
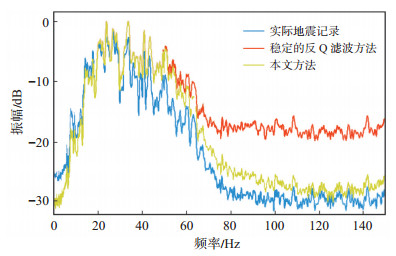
将本次研究方法用于实际地震记录,叠后地震记录如图 7(a)所示,虽然地震记录的整体信噪比较高,但仍有未被完全压制的随机干扰。图 7(b)为对图 7(a)中的地震剖面进行稳定的反Q滤波结果,其中Q值为150,增益限为10 dB。可以看到,深层地震记录的振幅能量增强,且分辨率有所提高,但地震记录也变得“粗糙”,这是因为反Q滤波也增强了随机噪声的能量。由图 7(c)可以看到,其分辨率明显得到改善,且地震剖面比图 7(b)“干净”,这是因为本次研究方法压制了部分随机噪声的能量。对图 7黄色虚线框内的地震剖面进行放大显示,如图 8所示。利用稳定的反Q滤波和本次研究方法处理得到的地震记录的分辨率都得到明显提高,但是稳定的反Q滤波方法处理后的剖面具有明显的“毛刺”,随机干扰能量较强;而利用本此研究方法处理得到的结果,明显改善了地震记录的分辨率,同时也压制了噪声能量。图 9为图 8中相应地震记录的归一化对数振幅谱,其中蓝线为原始地震记录,红线为稳定的反Q滤波结果,黄线为本次研究方法的处理结果。可以看到,与稳定的反Q滤波方法相比,基于时频域信噪比的自适应增益限反Q滤波方法在补偿高频振幅能量的同时,压制了部分高频带内的随机噪声,有效提高了地震记录的分辨率和信噪比。
|
下载原图 图 7 实际地震记录及不同反Q滤波方法处理结果 Fig. 7 Real seismic records and processing results of different inverse Q filtering methods |
|
下载原图 图 9 图 8中相应地震记录的归一化振幅谱 Fig. 9 Normalized amplitude spectra of the corresponding seismic records in Fig. 8 |
(1)基于时频域信噪比的自适应增益限反Q滤波方法利用时频域信噪比计算地震记录有效频带及相应的截止频率,对地震记录进行时变增益的振幅补偿,有效压制了部分高频噪声能量,明显改善了反Q滤波后地震记录的信噪比和分辨率。
(2)本次研究方法的关键在于如何有效选取时频域信噪比的阈值C0,进而估算有效频带和截止频率,其会直接影响自适应增益限反Q滤波的结果。
(3)本次研究方法在一定的信噪比限度内可取得较好的应用效果,随着信噪比的降低,其对噪声的压制效果逐渐变差。
| [1] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用. 石油物探, 2018, 57(3): 436-442. SONG J J, YU J Y, WANG C, et al. Q estimation for near-surface media and its application in the northern Tahe Oilfield, China. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. DOI:10.3969/j.issn.1000-1441.2018.03.013 |
| [2] |
REINE C, CLARK R, VAN DER BAAN M. Robust prestack Q -determination using surface seismic data: Part 1-Method and synthetic examples. Geophysics, 2012, 77(1): 45-56. DOI:10.1190/geo2011-0073.1 |
| [3] |
王本锋, 陈小宏, 李景叶, 等. 基于反演策略的数据自适应衰减补偿方法. 石油物探, 2014, 53(3): 304-312. WANG B F, CHEN X H, LI J Y, et al. Inversion based data-adaptive attenuation compensation method. Geophysical Prospecting for Petroleum, 2014, 53(3): 304-312. DOI:10.3969/j.issn.1000-1441.2014.03.008 |
| [4] |
刁瑞. 地震数据提高分辨率处理监控评价技术. 岩性油气藏, 2020, 32(1): 94-101. DIAO R. Monitoring and evaluation technology for high resolution processing of seismic data. Lithologic Reservoirs, 2020, 32(1): 94-101. |
| [5] |
WANG Y H. Inverse Q-filter for seismic resolution enhancement. Geophysics, 2006, 71(3): 51-60. DOI:10.1190/1.2192912 |
| [6] |
ZHAO Y, MAO N B. An inverse Q filtering approach based on a varying stabilization factor. Journal of Geophysics and Engineering, 2018, 15(4): 1269-1279. DOI:10.1088/1742-2140/aaae90 |
| [7] |
XUE Y J, CAO J X, WANG X J. Inverse Q filtering via synchro squeezed wavelet transform. Geophysics, 2019, 84(2): 121-132. |
| [8] |
MARGRAVE G F, LAMOUREUX M P, HENLEY D C. Gabor deconvolution: Estimating reflectivity by nonstationary deconvolution of seismic data. Geophysics, 2011, 76(3): 15-30. |
| [9] |
GHOLAMI A. Projected Gabor deconvolution. Geophysics, 2016, 81(2): 151-157. DOI:10.1190/geo2015-0412.1 |
| [10] |
ZHU T Y, HARRIS J M, BIONDI B. Q-compensated reversetime migration. Geophysics, 2014, 79(3): 77-87. DOI:10.1190/geo2013-0344.1 |
| [11] |
ZHAO Y, MAO N B, REN Z M. A stable and efficient approach of Q reverse-time migration. Geophysics, 2018, 83(6): 557-567. DOI:10.1190/geo2018-0022.1 |
| [12] |
WANG Y H. A stable and efficient approach of inverse Q filtering. Geophysics, 2002, 67(2): 657-663. DOI:10.1190/1.1468627 |
| [13] |
WANG Y H. Quantifying the effectiveness of stabilized inverse Q filtering. Geophysics, 2003, 68(1): 337-345. DOI:10.1190/1.1543219 |
| [14] |
刘财, 冯晅, 张瑾. 稳定的迭代法反Q滤波. 石油地球物理勘探, 2013, 48(6): 890-895. LIU C, FENG X, ZHANG J. A stable inverse Q filtering using the iterative filtering method. Oil Geophysical Prospecting, 2013, 48(6): 890-895. |
| [15] |
WANG S, CHEN X H. Absorption-compensation method by l1-norm regularization. Geophysics, 2014, 79(3): 107-114. |
| [16] |
张瑾, 刘财, 冯晅, 等. 波场延拓反Q滤波的正则化方法. 世界地质, 2013, 32(1): 123-129. ZHANG J, LIU C, FENG X, et al. Regularization method of inverse Q filtering based on wave field continuation. Global Geology, 2013, 32(1): 123-129. DOI:10.3969/j.issn.1004-5589.2013.01.016 |
| [17] |
李雪英, 沈加雪, 于生云, 等. 频域反Q滤波稳定性控制方法. 地球物理学进展, 2016, 31(4): 1608-1613. LI X Y, SHEN J X, YU S Y, et al. Stability control method of inverse Q filtering in frequency domain. Progress in Geophysics, 2016, 31(4): 1608-1613. |
| [18] |
ZHAO Y, LIU Y, LI X X, et al. Time-frequency domain SNR estimation and its application in seismic data processing. Journal of Applied Geophysics, 2014, 107: 25-35. DOI:10.1016/j.jappgeo.2014.05.002 |
| [19] |
张固澜, 林进, 王熙明, 等. 一种自适应增益限的反Q滤波. 地球物理学报, 2015, 58(7): 2525-2535. ZHANG G L, LIN J, WANG X M, et al. A self-adaptive approach for inverse Q-filtering. Chinese Journal of Geophysics, 2015, 58(7): 2525-2535. |
 2021, Vol. 33
2021, Vol. 33