2. 北京师范大学 统计学院, 北京, 100875;
3. 北京中地润德石油科技有限公司, 北京, 100083
2. School of Statistics, Beijing Normal University, Beijing 100875, China;
3. Beijing Zhongdirunde Petroleum Technology Co., Ltd., Beijing 100083, China
横波速度[1]是储层岩石物理分析、AVO正演、AVO属性分析以及叠前反演等[2-4]工作必不可少的基础信息,通过纵横波速度信息的结合可以有效地提高储层(气层、差气层、干层等)流体预测精度,减少地震振幅解释的多解性。横波速度一般是通过偶极子声波得到,测试费用较高且技术不完善[5-7],导致在多数地区的实际生产中横波速度测井资料十分匮乏或者数据质量较差。因此,如何解决横波速度的精确预测问题成为油气勘探的重要研究内容之一。
目前研究人员针对岩性油气藏的横波波速预测已经开展了大量的研究[8-10],主要分为经验公式法、理论公式法和基于机器学习的模型拟合等3种方法。其中经验公式容易实现,计算效率高,但拟合关系式反映了大量测井数据的统计规律,在实际应用时存在较大误差;理论公式法中,Xu等[11]提出了Xu-White模型与Xu -Payne模型,其利用岩石物理建模法预测横波速度精度较高,但是算法复杂、所需参数较多,导致计算效率较低。地震岩石物理学的主要研究方向是研究岩石弹性参数(如速度、密度、波阻抗、纵横波速度比等)与储层参数(如孔隙度、孔隙储层类型、储层饱和度等)的关系,因此可以通过建立横波速度和储层参数之间的高精度机器学习拟合模型对横波速度进行预测。随着人工智能等技术的发展,基于测井参数,采用机器学习算法开展横波速度预测的方法引起众多学者关注[12-13],其中目前已经有使用提升树[14]、XGBoost[15-16]与支撑向量机[17]等方法预测相关参数。但考虑到测井参数是对不同地层沉积特征的不同响应,整体具有一定的空间时序特征,而多数传统机器学习方法中没有结合空间时序信息,对于其整体预测结果不全面。2006年,Hinton等[18]提出了深度学习概念后其方法已经应用于多种领域[18-19]。对于地球物理领域,Eskandair等[20]率先使用神经网络预测地球物理参数,孙宇航等[21]利用GRU网络预测横波速度。基于卷积运算的深度神经网络对于包含邻域空间信息的数据有良好的表达能力。
根据卷积神经网络对空间时序特征表征的优势以及测井参数的一维时序特征,提出了基于测井参数的一维卷积神经网络(1D-CNN)的横波速度预测方法。先通过测井参数分析,选择对横波速度较为敏感的测井参数;再基于测井参数开展1D-CNN的应用效果分析,并开展了与传统岩石物理模型(Xu-White模型)、常规机器学习方法(人工神经网络、支持向量机、随机森林、XGB、LightGBM)的对比分析研究,最后结合测井参数相关性与地质学含义,分析了不同测井参数组合、不同岩性储层下横波速度预测效果。
1 数据背景研究区位于内蒙古自治区乌审旗境内,南部临近陕西省靖边县,东部紧邻横山县。区域构造处于鄂尔多斯盆地伊陕斜坡北部,目的层段为上古盒8段—山西组的水下三角洲前缘沉积的碎屑岩储层。经过筛选,选择W1井中一段连续的共计140 m的测井段作为研究对象,其采样间隔为0.125 m,共计1 376个样本点。盲井选择Li2井中一段续的共计150 m的测井段作为测试对象,其采样间隔为0.125 m,共计1 201个样本点。
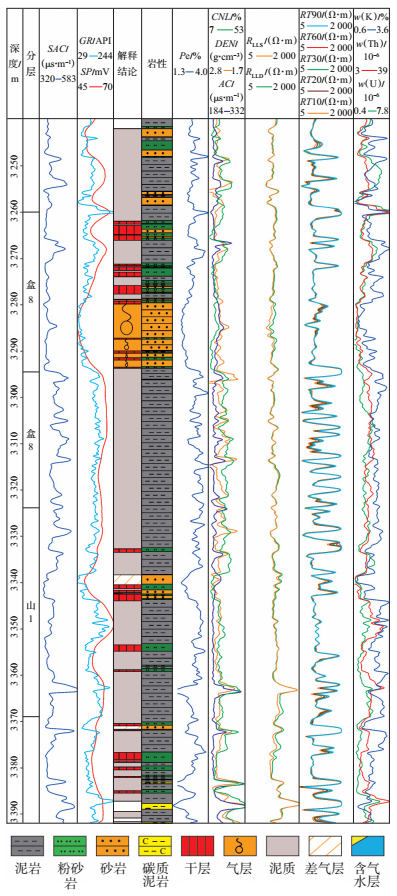
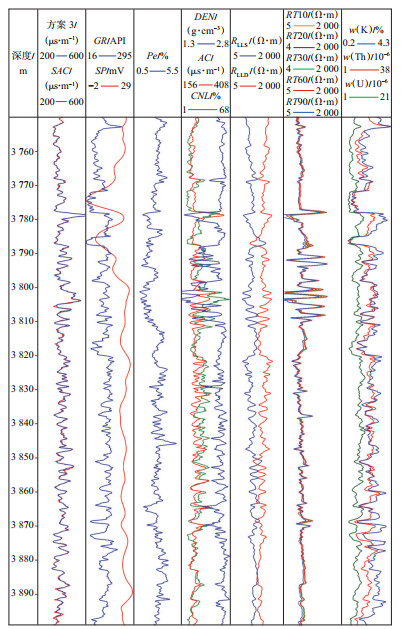
图 1为目的层段的碎屑岩层测井综合解释成果图,包含常规测井数据、阵列感应测井、放射性测井、测录井岩性及测井解释成果等。该井段包含砂岩、粉砂岩、泥岩以及少量的碳质泥岩等多种岩石类型,储层类型分为干层、含气层和气层等。
|
下载原图 图 1 苏里格气田W1上古生界碎屑岩储层井综合柱状图 Fig. 1 Comprehensive histogram of W1 Upper Paleozoic clastic reservoir of Sulige gas field |
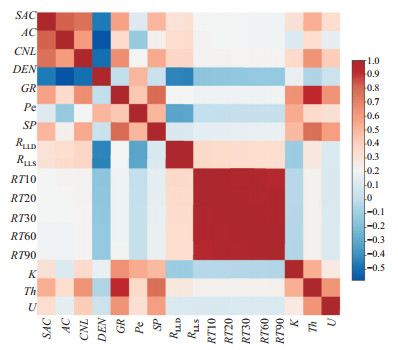
测井参数是对地层沉积、成岩、储集空间及其所含储层特征的综合响应,不同的测井参数能够反应地层的岩性、储集性、渗透性和含油气特征等,尽管在敏感性上存在差异,但基于对同一地层探测的不同测井参数之间必然存在着必然的联系。测井参数之间的相关性分析(图 2)也表明了这种内在联系的存在,但同时不同测井参数之间的相关性存在较大的差异,说明不同测井参数是从不同机理、不同特征或不同角度对地层的响应,测井参数包含了丰富多样的信息,这是利用测井参数进行横波速度预测的数据基础。纵、横波速度测井主要反应储层岩性、孔隙度特征,同时受储层的岩石骨架和孔隙储层性质的影响,因此纵、横波速度之间存在较强的正相关关系,但纵波波速受地层储集空间及其储层性质的影响更为显著,而横波速度与储层基质特征之间的关系更为密切,所以在孔隙度较高的含气层层段,纵横波速度之间相关性要明显低于较为致密的岩性段;密度参数直接参与储层体积模量和剪切模量的计算,间接参与横波速度的计算,密度与横波速度具有负相关性;补偿中子可以给出不同岩性中孔隙度较为准确的解释,可以确定地层孔隙度、矿物含量,与密度曲线重叠可以大致判断出气层,与横波速度具有一定相关性;伽马能谱反映了储层骨架中的泥质含量,可以判断储层岩性,与横波速度具有正相关关系;储层的岩石骨架通常不导电,电阻率主要反映储层的孔隙储层特征,因此也能在一定程度反映横波速度在储集性地层中的特征。
|
下载原图 图 2 苏里格气田W1上古生界储层测井参数相关性 Fig. 2 Correlation of logging parameters of W1 Upper Paleozoic reservoir in Sulige gas field |
测井参数在测量时每个点收集的数据都有一个承载范围,横波速度在收集过程中需要依靠不同距离的触发器提供地层改变部分的测量结果,代表该测量点周围一个深度范围的整体数据。因此在对横波速度进行预测时需要结合测井参数的数据承载考虑空间信息。
传统机器学习方法对于数据特征的学习多为点对点的方式,无法学习到数据的空间特征。卷积神经网络通过深度上的逐层卷积的方式,可以有效提取数据的空间特征
2.1 卷积神经网络卷积神经网络是机器学习方法中的一种深度前馈人工神经网络。卷积神经网络的基本结构一般由输入层、卷积层(Convolutional Layer)、池化层(Pooling Layer)、全连接层和判别器组成。网络迭代分为正向传播与反向传播两部分[22-23]。
正向传播中,网络中的一组卷积核对前一层输出的所有特征图进行卷积运算后得到新的特征图。网络使用权重共享机制,使用多组卷积核用于检测输入数据中的不同特征。对每个卷积核的运算结果使用连续可导的非线性激活函数,将输出值限制在一个合适的阈值区间,可以有效增加网络运算效率。
| $ {x^l} = f({W^l}{x^{l - {\rm{1}}}} + {b^l}) $ | (1) |
式中:xl为第l层的输出;W l为第l层的权重(卷积核);bl为第l层的偏移量;激活函数f(x)一般使用ReLU或sigmoid函数。
网络通过反向传播更新权重,从而优化特征提取效果,最终获得较优的预测效果。反向传播时,网络判别器计算网络预测值与真实值之间的损失值传播进入网络,从后向前逐层更新网络中的权重,使网络进入最优区间,下一次正向传播的损失值减小,形成迭代学习。
| $ E = Loss(t, y) $ | (2) |
| $ {\delta ^l} = {({W^{l + {\rm{1}}}})^T}{\delta ^l}^{ + 1}f'({u^l}) $ | (3) |
| $ \frac{{\partial E}}{{\partial {W^l}}} = {x^{l - {\rm{1}}}}{({\delta ^l})^T} $ | (4) |
| $ \Delta {W^l} = - \eta \frac{{\partial E}}{{\partial {W^l}}} $ | (5) |
式中:E为真实值与预测值之间的误差;t,y分别为样本真值与预测值;Loss(t)为网络的损失函数;δl为第l层的敏感度;ΔW l为第l层的权重变化量。
卷积神经网络通过局部连接、权值共享等操作特性使之可以有效地降低网络的复杂度,减少训练参数的数目,并使算法具有较强鲁棒性,且易于训练。
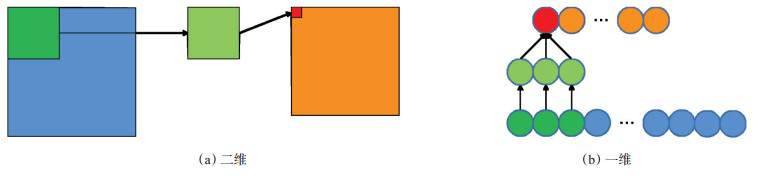
2.2 一维卷积神经网络本文研究的测井参数属于一维序列数据,因而采用一维卷积方法根据原数据深度截取上下邻域。对每一种测井参数做一维卷积运算提取相邻深度的特征信息。最后网络将提取得到的特征向量拼接,传入全连接层进行预测,图 3为其卷积结构图。
|
下载原图 图 3 卷积运算过程示意图 Fig. 3 Convolution operation process diagram |
基于1D-CNN的横波速度预测过程描述如下:首先将模型样本数据分为训练数据集和测试数据集。然后将训练数据集输入到1D-CNN结构中,网络结构中的卷积层与全连接层相连,得到横波速度预测值,并与实际的横波速度数据对比计算误差函数。基于误差进行反向传播训练网络权重得到最优结果。最后将测试数据集输入到最优的网络模型中,得到测试集对应的横波预测序列。试验程中,网络结构涉及的参数包括网络隐藏层数、卷积尺度大小与数量、批尺寸(每次训练时训练数据的样本点数),通过训练过程选择最优的参数。
网络使用Adam(Adaptive moment estimation)优化算法。Adam算法是一种自适应参数更新算法,通过更新和计算影响模型训练和输出的网络参数,使其逼近最优解,从而最小化损失值。其更新参数方法为
| $ {m_{\rm{t}}} = {\beta _{\rm{1}}}{m_{{\rm{t}} - {\rm{1}}}} + ({\rm{1}} - {\beta _{\rm{1}}}){g_{\rm{t}}} $ | (6) |
| $ {\nu _{\rm{t}}} = {\beta _{\rm{2}}}{\nu _{{\rm{t}} - {\rm{1}}}} + ({\rm{1}} - {\beta _{\rm{2}}})g_{\rm{t}}^{\rm{2}} $ | (7) |
| $ {\hat m_{\rm{t}}} = \frac{{{m_{\rm{t}}}}}{{{\rm{1}} - \beta _{\rm{1}}^t}} $ | (8) |
| $ {\hat \nu _{\rm{t}}} = \frac{{{\nu _{\rm{t}}}}}{{{\rm{1}} - \beta _2^t}} $ | (9) |
| $ {\theta _{{\rm{t}} + {\rm{1}}}} = {\theta _{\rm{t}}} - \frac{\eta }{{\sqrt {{{\hat \nu }_{\rm{t}}} + \varepsilon } }}{\hat m_{\rm{t}}} $ | (10) |
式中:β1,β2为指数衰减率;mt,νt分别为梯度的移动均值和平方梯度;
为对比模型的预测效果,使用均方根误差、可决系数和相关系数表达实际值与预测值之间的偏差。均方误差(mean-square error,MSE)是反映估计量与被估计量之间差异程度的一种度量,通常在应用中均方误差越小说明模型的预测值与真实数据越接近,模型对数据分布的表达能力越强。可决系数(R2)表示一个随机变量与多个随机变量关系的数字特征,是用来反映回归模型中因变量变化可靠程度的一个统计指标。可决系数越接近于1,说明模型的预测效果越好。相关系数(ρ)反映两个变量间每个单位变化的相似程度,越接近于1说明变量变化趋势越一致。
| $ RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^n {{{\left( {{y_i} - {{\hat y}_i}} \right)}^2}} } $ | (11) |
| $ {R^2} = 1 - \frac{{MSE({y_i},{{\hat y}_i})}}{{\frac{1}{n}\sum\nolimits_{i = 1}^n {{{({y_i} - \bar y)}^2}} }} $ | (12) |
| $ \rho = \frac{{Cov(y,\hat y)}}{{{\sigma _{\rm{y}}}{\sigma _{{\rm{\hat y}}}}}} $ | (13) |
式中:y为真实数据;ŷ为预测结果;m,n为样本数量。
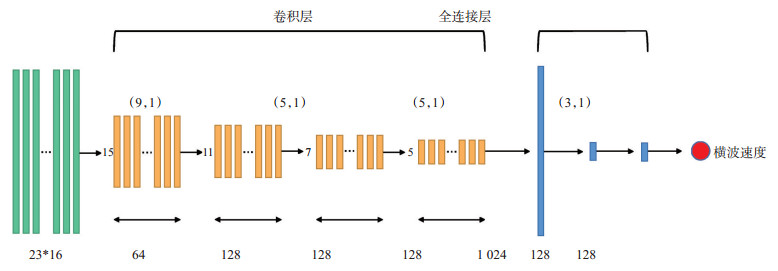
2.3 1D-CNN横波速度预测网络架构图 4为试验所使用的1D-CNN模型,模型使用4个卷积层和3个全1连接层,卷积层的节点个数为64,128,128,128,全连接层节点个数为1 024,128,128。经过试验对比分析,1D-CNN在网络浅层部分使用较大卷积核提取更大范围的邻域信息效果更好,之后再向深层推进的过程中减小卷积核的大小,每层一维卷积的大小为9,5,5,3。对于1DCNN,考虑到数据在经过卷积操作后进入ReLU与sigmoid激活函数,数据进行归一化处理,保持数据在经过激活函数映射的敏感区间能够保留更多特征信息,使预测效果更加精准。采用Adam算法进行优化,考虑到预测过程中的过拟合问题,模型采用了dropout,丢失概率为25%。
|
下载原图 图 4 一维卷积神经网络结构 Fig. 4 1D-CNN structure |
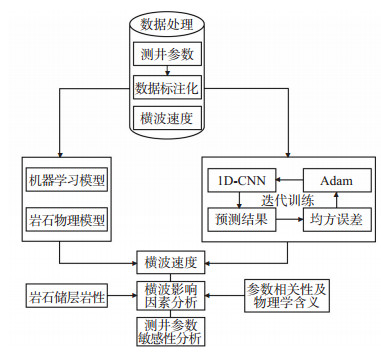
图 5为整个研究的工作流程图。由于各测井参数的取值范围不一样,直接使用原始测井参数进行预测对于一些算法影响较大,在进行预测前需要对数据进行预处理将数据标准化到一定的范围中。并分析横波速度与测井参数之间的相关性;其次使用1D-CNN算法对横波速度进行预测,并使用岩石物理模型、机器学习算法对预测结果进行对比分析;最后分析预测过程中不同测井参数的组合对不同岩性、不同储层预测结果的影响。
|
下载原图 图 5 一维卷积神经网络模型工作流程 Fig. 5 Workflow of 1D-CNN model |
试验在Intel(R)Core(TM)i5-9 400 CPU @ 2.90 GHz,NVIDIA GeForce RTX 2 060环境上运行,使用Python3.7编译环境,版本为1.3.0的Py-Torch深度平台。共计1 376个样本点,采用声波时差(AC)、自然伽马(GR)、补偿中子测井(CNL)、密度测井(DEN)、光电吸收截面指数(Pe)、深测向电阻率(RLLD)、浅侧向电阻率(RLLS)、阵列感应电阻率(RT10,RT20,RT30,RT60,RT90)和放射性元素(K,U,Th)等16种测井参数。按照1∶1的比例随机将数据划分为训练集和测试集进行试验。对于1D-CNN的输入数据,取该采样点上下1.375 m(即23个采样点)作为局部空间信息。
3.2 不同横波速度预测方法对比基于传统的岩石物理模型方法的横波预测过程:研究使用Xu-White模型开展了横波速度的预测。通过上述地质背景分析该地区碎屑岩储层岩石物理模型。首先通过测井解释得到储层孔隙度、含气饱和度,同时根据已知的纵波速度、密度,采用Xu-White模型进行了横波预测。通过测井解释方法确定Xu-White模型中每种矿物及储层组分。
基于机器学习算法的横波预测过程:根据测井参数中的16种测井参数结合人工神经网络(BP)、支持向量机(SVR)、随机森林(RF)、XGB、LightGBM等模型对横波速度进行回归预测、对比均方根误差。[20-22]
储层基于1D-CNN的横波预测过程:根据测井参数中的深度信息提取测井参数相邻深度的数据信息,将测井参数组合成16组一维数据;然后建立1D-CNN预测模型,进而得到预测横波速度。
表 1中计算不同方法实测横波速度与预测横波速度均方根误差,可以看出相比基于岩石理论公式、支持向量机、决策树的算法,基于1D-CNN的回归算法的均方根误差较小(0.741 μs/m),预测效果较好。其预测结果与真实结果整体趋势一致,可决系数达到0.96,相关系数达到0.98。
|
|
下载CSV 表 1 不同算法预测横波结果 Table 1 Different algorithms predict shear wave results |
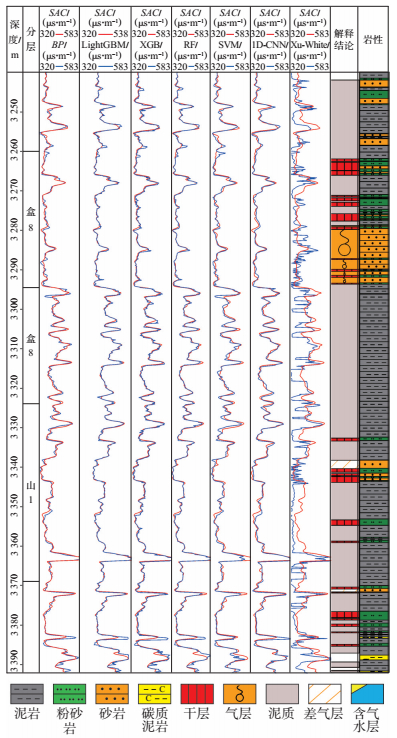
图 6中为不同方法预测结果,从图中可以看出,基于1D-CNN算法的预测结果与实际结果之间的误差相比于其他算法更小,曲线重合度更高,说明1D-CNN对于具有空间特征的数据预测具有更明显的优势。
|
下载原图 图 6 苏里格气田W1上古生界储层横波预测结果对比 Fig. 6 Comparison of shear wave prediction results of W1 Upper Paleozoic reservoir in Sulige gas field |
测井参数与横波速度间关系较为复杂,导致某些测井参数对于某种指示作用影响过大,降低横波速度预测精度。为解决测井参数的选择问题,根据不同测井参数在地质分析中的相关性与获取的难易程度设计为10种试验方案设计。通过不同的实验方案得到的预测结果,分析测井参数对碎屑岩储层不同岩石、储层结构中横波预测的影响,具体方案设计如下:储层
方案1:使用16种测井参数:AC,CNL,DEN,GR,Pe,SP,RLLD,RLLS,RT10,RT20,RT30,RT60,RT90,K,Th,U;
方案2:使用13种测井参数:AC,CNL,DEN,GR,Pe,SP,RLLD,RLLS,RT10,RT20,RT30,RT60,RT90;
方案3:使用8种测井参数:AC,CNL,DEN,GR,Pe,SP,RLLD,RLLS;
方案4:使用7种测井参数:AC,CNL,DEN,GR,Pe,RLLD,RLLS;
方案5:使用7种测井参数:AC,CNL,DEN,GR,SP,RLLD,RLLS;
方案6:使用6种测井参数:AC,CNL,DEN,GR,Pe,SP;
方案7:使用5种测井参数:AC,CNL,DEN,GR,Pe;
方案8:使用5种测井参数:AC,CNL,DEN,GR,SP;
方案9:使用3种测井参数:AC,GR,Pe;
方案10:使用3种测井参数:AC,GR,SP。
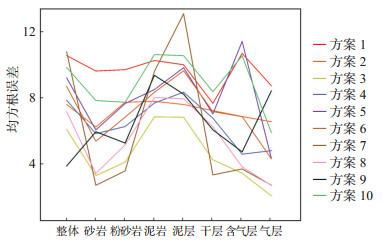
如图 7所示,从实测数据和预测结果对比,在使用8种测井参数时效果最好,均方根误差较小,经过计算可决系数达到0.98。结合测井参数实际含义,在加入或移除一些测井参数后,由于卷积运算造成的数据特征平均化,测井参数的指示作用发生偏移,使模型过于重视或忽略其它解释方向,对于某些岩性段、不同储层类型储层段的横波预测结果会发生较大偏移,整体预测效果变差。
|
下载原图 图 7 苏里格气田W1上古生界储层不同参数组合预测横波结果 Fig. 7 S-wave prediction results of different parameters combination of W1 Upper Paleozoic reservoir in Sulige gas field |
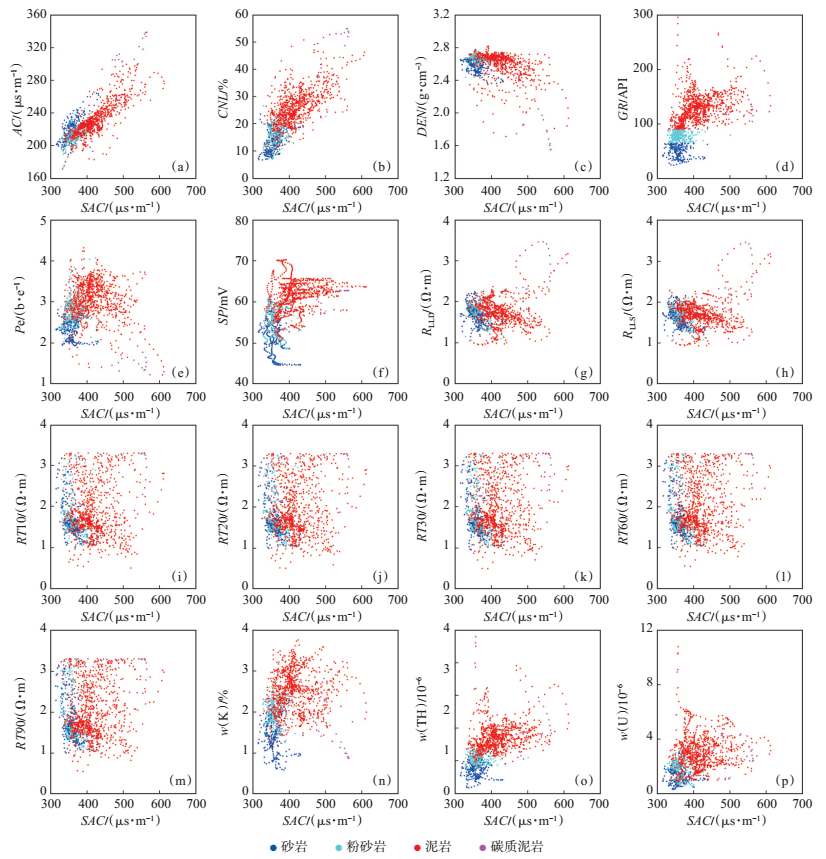
通过对不同的岩性及储层类型储层的横波速度与测井参数之间的交会图(图 8),可以分析不同测井参数与横波速度之间的相关性,并指示其在横波速度预测中的重要性。
|
下载原图 图 8 苏里格气田W1上古生界储层测井参数与横波速度交会图 Fig. 8 Cross plot of logging parameters and shear wave velocity of W1 Upper Paleozoic reservoir in Sulige gas field |
(1)泥质含量较高的粉砂岩和泥岩其横波速度与伽马能谱呈现正相关关系,且相关性较强。说明伽马能谱参数(K,U,Th)主要在指示泥质成分的含量。
(2)电阻率参数主要反映储层孔隙中的储层电性特征,对储层类型及其饱和度储层较为敏感。从整体上看,横波速度和电阻率之间的相关性在砂岩、粉砂岩及泥岩中相对较弱。说明电阻率参数对于横波预测的指示作用主要表现在储层性质上,对于储集性较好、孔隙度较高的含气层段指示作用较大。
(3)自然电位参数主要反映储层中的水与泥浆的相对矿化度,主要反应储层的渗透性,对于横波速度的预测指示作用相对较小。
(4)补偿中子在测井解释常与密度曲线重叠判断储层的含气性,主要指示地层孔隙度和矿物含量信息,因而对横波速度预测有一定的作用。
表 2为不同预测方案对不同岩性及储层类型的横波预测误差。对比方案1,2可知,GR与K,U,Th参数均反应岩石的泥质含量信息,过多同质参数的加入会造成维度的增高及信息冗余,会在一定程度上降低模型的学习效果,进而降低横波速度预测的效果,去掉K,U,Th参数后,预测效果整体变好。同样,阵列感应电阻率与深、浅侧向电阻率包含类似的信息,去掉阵列感应电阻率,而加入深、浅侧向电阻率参数时,不仅保留了对储层信息的指示信息,而且降低了参数维度,因此横波速度预测精度整体变好(方案3,6),反之,预测效果变差。
|
|
下载CSV 表 2 不同方案预测均方根误差 Table 2 RMSE of different schemes |
方案9和方案10表明,仅纵波速度和反应岩性的曲线如GR,Pe,SP等为基础,1D-CNN依然可以一定精度的横波速度预测结果,两个方案预测误差分别问8.423 μs/m和9.846 μs/m,明显优于Xu-White模型。与方案3到方案8对比,当测井参数比较齐全时,Pe,SP加入或缺失,对横波速度预测结果的影响并不十分显著,说明不同测井参数之间在反应岩性特征方面存在一定的重叠,同时又在储层类型和储层特征的表达上存在互补性。
所以适合的测井参数选择及组合,对于横波速度预测而言极为重要。针对不同的岩石类型和储层类型需要选择对其敏感的测井参数才能取得预期目标,而过多的信息冗余会影响1D-CNN模型学习效果,进而降低横波预测的精度。对于研究区碎屑岩储层而言,常规测井与深浅电阻率等8种测井参数的组合横波预测精度最高,仅为7.56μs/m。
3.4 盲井预测结果图 9为盲井测试结果,可以看到在使用方案3进行测试时预测的横波速度,均方根误差为8.024,可决系数为0.962,相关系数为0.981,结果较为合理,说明该模型泛化能力较好,可以在不同地区中应用。
|
下载原图 图 9 苏里格气田上古生界储层盲井预测结果 Fig. 9 Blind well prediction results of Upper Paleozoic reservoir in Sulige gas field |
(1)一维卷积神经网络是一种可行的、适用于测井参数预测的深度学习方法,对比岩石物理参数预测的理论模型和常规机器学习模型,一维卷积神经网络在提取测井参数空间时序特征方面具有先天的优势,因此该模型更适用于横波速度的预测。
(2)相比传统Xu-White模型及机器学习方法,1D-CNN方法是横波预测提供一种更有效的方法,其预测结果与实际横波速度之间的误差较小、可决系数和相关系数较高。
(3)岩石物理学理论研究表明测井参数反映了不同地质时间的岩性、沉积特征,因此不同测井参数对横波速度都有一定的指示作用,同时这种指示作用与岩性、物性及含气性有很大的关系。在通过10组试验说明过多同质参数的加入会造成维度的增高及信息冗余,不同测井参数之间在反应岩性特征方面存在一定的重叠,同时又在储层类型和储层特征的表达上存在互补性。常规测井与深浅电阻率等8种测井参数的组合预测精度最高。
(4)基于一维卷积的深度学习算法是一种以数据为驱动,挖掘数据中内在的、深度关系的机器学习模型,其预测精度依赖于训练样本的精度与样本数据分布,对原始数据要求高,同时深度学习模型在专业领域的应用还需要增强在专业理论层面的可解释性,以推广智能学习模型在专业领域的应用。
| [1] |
谢冰, 白利, 赵艾琳, 等. Sonic Scanner声波扫描测井在碳酸盐岩储层裂缝有效性评价中的应用: 以四川盆地震旦系为例. 岩性油气藏, 2017, 29(4): 117-123. XIE B, BAI L, ZHAO A L, et al. Application of sonic scanner logging to fracture effectiveness evaluation of carbonate reservoir: A case from Sinian in Sichuan Basin. Lithologic Reservoirs, 2017, 29(4): 117-123. |
| [2] |
丁燕, 杜启振, 刘力辉, 等. 基于纵横波同步联合的孔隙模量三参数AVO反演方法. 岩性油气藏, 2020, 32(1): 111-119. DING Y, DU Q Z, LIU L H, et al. Three-parameter AVO inversion method of pore modulus based on PP and PS wave simultaneous joint inversion. Lithologic Reservoirs, 2020, 32(1): 111-119. |
| [3] |
张艳, 高世臣, 孟婉莹, 等. 致密砂岩储层AVO正演模拟过程中的不确定性分析. 岩性油气藏, 2020, 32(6): 120-128. ZHANG Y, GAO S C, MENG W Y, et al. Uncertainty analysis in AVO forward modeling for tight sandstone reservoirs simultaneous joint inversion. Lithologic Reservoirs, 2020, 32(6): 120-128. |
| [4] |
CASTAGNA J P, BATZLE M L, KAN T K, et al. Offset-dependent reflectivity-theory and practice of AVO analysis Investigations in Geophysics, 1993, 8: 135-171.
|
| [5] |
RØGEN B, GOMMESEN L, FABRICIUS I L. Methods of velocity prediction tested for North Sea chalk: A review of fluid substitution and S estimates. Journal of Petroleum Science & Engineering, 2004, 45(1-2): 129-139. |
| [6] |
BERRYMAN J G. Poroelastic shear modulus dependence on pore-fluid properties arising in a model of thin isotropic layers. Geophysical Journal International, 2004, 157(1): 415-425. DOI:10.1111/j.1365-246X.2004.02184.x |
| [7] |
CASTAGNA J P, BATZLE M L, EASTWOOD R L. Relationships between compressional-wave and shear wave velocities in clastic silicate rocks. Geophysics, 1985, 50: 571-581. DOI:10.1190/1.1441933 |
| [8] |
MA X H, YANG Y, WEN L, et al. Distribution and exploration direction of medium-and large-sized marine carbonate gas fields in Sichuan Basin, SW China. Petroleum Exploration and Development, 2019, 46(1): 1-13. DOI:10.1016/S1876-3804(19)30001-1 |
| [9] |
LI Y, KANG Z J, XUE Z J, et al. Theories and practices of carbonate reservoirs development in China. Petroleum Exploration and Development, 2018, 45(4): 669-678. |
| [10] |
张录录. 典型油气藏岩石物理特征分析及应用研究. 青岛: 中国石油大学(华东), 2013. ZHANG L L. Analysis of rock physics characteristics of typical reservoir and applied research. Qingdao: China University of Petroleum (East China), 2013. |
| [11] |
XU J, TAN M, WANG X, et al. Predicting acoustic-wave velocities and fluid sensitivity to elastic properties in fractured carbonate formation. Interpretation, 2017, 5(1): SB69-SB80. DOI:10.1190/INT-2016-0067.1 |
| [12] |
ZHANG Y, ZHONG H R, WU Z Y, et al. Improvement of petrophysical workflow for shear wave velocity prediction based on machine learning methods for complex carbonate reservoirs. Journal of Petroleum Science and Engineering, 2020, 192: 107234. DOI:10.1016/j.petrol.2020.107234 |
| [13] |
张炜, 唐宇, 余迎. 机器学习在地球物理测井中的应用进展. 测井技术, 2020(2): 185. ZHANG W, TANG Y, YU Y. Application progress of machine learning in geophysical logging. Well Logging Technology, 2020(2): 185. |
| [14] |
江凯, 王守东, 胡永静, 等. 基于Boosting Tree算法的测井岩性识别模型. 测井技术, 2018, 42(4): 395-400. JIANG K, WANG S D, HU Y J, et al. Lithology identification model by well logging based on boosting tree algorithm. Well Logging Technology, 2018, 42(4): 395-400. |
| [15] |
CHEN T Q, GUESTRIN C. XGBoost: A scalable tree boosting system. Proceedings of the 22nd ACM sigkdd international conference on knowledge discovery and data mining. San Francisco, 2016: 785-794.
|
| [16] |
孙予舒, 黄芸, 梁婷, 等. 基于XGBoost算法的复杂碳酸盐岩岩性测井识别. 岩性油气藏, 2020, 32(4): 98-106. SUN Y S, HUANG Y, LIANG T, et al. Identification of complex carbonate lithology by logging based on XGBoost algorithm. Lithologic Reservoirs, 2020, 32(4): 98-106. |
| [17] |
倪维军, 李琪, 郭文惠, 等. 基于支持向量机的页岩储层横波速度预测. 西安石油大学学报(自然科学版), 2017, 32(4): 46-49. NI W J, LI Q, GUO W H, et al. Prediction of shear wave velocity in shale reservoir based on support vector machine. Journal of Xi'an Shiyou University(Natural Science), 2017, 32(4): 46-49. DOI:10.3969/j.issn.1673-064X.2017.04.007 |
| [18] |
HINTON G E, SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks. Science, 2006, 313(5786): 504-507. DOI:10.1126/science.1127647 |
| [19] |
赵军龙, 李纲, 麻平社, 等. 神经网络在石油测井解释中的应用综述. 地球物理学进展, 2010, 25(5): 1744-1751. ZHAO J L, LI G, MA P S, et al. The application of network technology to petroleum logging interpretation. Progress in Geophysics, 2010, 25(5): 1744-1751. |
| [20] |
ESKANDARI H, REZAEE M, MOHAMMADNIA M. Application of multiple regression and artificial neural network techniques to predict shear wave velocity from wireline log data for a carbonate reservoir, South-West Iran. CSEG Recorder, 2004, 29(7): 40-48. |
| [21] |
孙宇航, 刘洋. 利用GRU神经网络预测横波速度. 石油地球物理勘探, 2020, 55(3): 484-492. SUN Y H, LIU Y. Prediction of S-wave velocity based on GRU neural network. Oil Geophysical Prospecting, 2020, 55(3): 484-492. |
| [22] |
SUYKENS J A K, VANDEWALLE J. Least squares support vector machine classifiers. Neural Processing Letters, 1999, 9(3): 293-300. DOI:10.1023/A:1018628609742 |
| [23] |
GOODFELLOW I, BENGIO Y, COURVILLE A, et al. Deep learning. Cambridge: Massachusetts Institute of Technology Press, 2016.
|
 2021, Vol. 33
2021, Vol. 33




