2. 中国石油大学 (北京) 石油工程学院, 北京 102249
2. College of Petroleum Engineering, China University of Petroleum(Beijing), Beijing 102249, China
渤海目前开发的主力油田为高孔高渗的普通稠油油藏。初期一般采取大井距的反九点基础井网,较高的采油速度进行开发。在进入高含水期前后,为提高油田开发效果,常采用转注或加密等调整方式对基础井网进行调整。对于一些条件适宜的油藏和层位,常考虑在反九点井网的基础上,整体加密水平井构成组合井网进行深度开发[1-3]。
将水平井加密到基础直井井网形成组合井网,可充分利用基础井网以节约成本,同时可增强区域的生产能力,有利于水驱均衡驱替。加密水平井的方式主要有两大类。一类采取局部、不规则的井网加密方式,在潜力富集区挖掘剩余油潜力,对原注采井网的驱替状况影响较小;另一类采取整体加密的方式,与原注采井网形成组合井网,以”直井注-水平井采”的形式构建新的注采系统,可以整体改变或调整原直井井网的驱替方向及驱替效果,较大地提高原井网储量的动用程度[4-8]。
关于加密水平井的可行性和部署策略的理论研究,大部分学者主要分析油井的产能、含水等指标变化[9-14],而针对水平井加密后井间储量动用效果的评价较少。对于水平井部署界限,大多利用数值模拟软件,以采出程度、含水率等指标作为水平井加密参数的选择依据[15-20],少有通过分析渗流场研究平面驱替规律,从井间动用程度来评价开发效果的研究[21],而海上油田开发风险性高,投资成本大,须全面、深入研究以确定井网合理调整技术策略。本文基于渤海实际油田,考虑油田特点建立渗流模型,研究水平井部署后注采单元渗流场变化,以及注采单元储量有效动用规律,分析不同因素对提高储量动用效果的影响,进而确定水平井合理加密技术界限,为后期结合油藏实际模型的数值模拟等相关研究奠定理论基础。
1 渤海水驱稠油油田注采井网调整设想渤海HD油田的产层为河流相沉积的高孔高砂岩储层,平均孔隙度为30%,平均渗透率为2 330 mD,地下原油黏度为52 mPa·s,主力层有效厚度超过20 m。初期采用350 m×350 m的反九点基础井网进行注水开发。受井网密度较低、注采井距较大和水驱稠油渗流阻力大等影响,在开发过程中逐渐表现出主渗流方向水驱见效快,存在一定的各向异性,导致油藏水驱有效单元程度低、油井水驱受效弱等问题。在进入中高含水阶段后,油田产量难以满足海上油田高效开发的要求,迫切需要在主力油层上进行针对性地注采井网调整,提高水驱开发效果。
根据油田地质特点、开发状况和开发需求,拟基于目前的350 m×350 m的反九点基础井网[图 1(a)],在直井井排之间整体加密水平井,原直井井网中的油井全部转注,形成“直井注-水平井采”的交错排状组合井网[图 1(b)]。

|
下载原图 图 1 注采井网加密水平井基本形式 Fig. 1 Fundamental form of combined well pattern |
在原直井反九点注采井网中,由于对角线方向注采井距大,该方向上水驱稠油驱替效果较差。另外注水井偏少,整体水驱波及系数较小,注采速度受到限制。在原井网井排之间的弱动用区加密水平井,可以利用水平井的优势,强化该区域的动用效果;另一方面,将原油井转注,使得注采井数比达到1∶1,可以增加水平井的受效方向,增大水平井的水驱受效面积,提高水驱效果,同时可以满足开发后期提液强化水驱开发的需要。
2 加密水平井注采井网单元渗流模型的建立及求解基于典型井网形式,根据井网调整设想,建立组合井网渗流模型,研究加密水平井后对基础反九点井网渗流场的影响。
2.1 加密水平井基础注采井组中势的求解 2.1.1 基本渗流模型及变换关系加密水平井注采井网条件下的渗流模型基本假设条件为:①油藏中流体为单相流体。②油藏中流动为稳定渗流。③刚性渗流,不考虑岩石及流体压缩性。④地层中流体的渗流符合达西定律。
根据渗流力学理论,为求解方便,将物平面Z中的渗流问题,通过保角变换转换至像平面W中进行求解,再将解析解通过逆变换到物平面Z中即可。
在物平面Z中,基于图 1所示的井间内部加密水平井的完整注采单元,由对称性原则,选取其中加密水平井基础注采井组(即“直井注-水平井采”的直接对应区域)进行渗流模型的建立与研究。该注采井组由“水平采油井与四角直井注水井”组成(图 2)。

|
下载原图 图 2 加密水平井基础注采井组物平面Z示意图 Fig. 2 Schematic diagram of Z object plane of basic injec‐ tion-production well group of infilled horizontal wells |
在加密水平井基础注采井组中,以水平井中心为原点建立平面直角坐标系,其中水平井长度为2 L,井网排距与井距均为d。
根据组合井网基本注采对应关系,利用渗流力学中保角变换对物平面Z进行映射、转换。取保角变换函数
| $ z = L{\rm{ch}}w $ | (1) |
其中:z = x + yi; w = ξ + ηi。
根据式(1)得到物平面Z与像平面W平面坐标对应关系为
| $ \{ _{y = L{\rm{sh}}\xi \sin \eta }^{x = L{\rm{ch}}\xi \cos \eta } $ | (2) |
由式(2)可得
| $ \frac{{{x^2}}}{{{L^2}{\rm{ch}}{\xi ^2}}} + \frac{{{y^2}}}{{{L^2}{\rm{sh}}{\xi ^2}}} = {\cos ^2}\eta + {\sin ^2}\eta = 1 $ | (3) |
根据公式(3)可以解得物平面Z上相应的(x,y)与像平面W的位置对应关系为
| $ \begin{array}{l} {\rm{c}}{{\rm{h}}^2}\xi {\rm{ = }}\frac{1}{{2{L^2}}}[{x^2} + {y^2} + {L^2} + \sqrt {{{({x^2} + {y^2} + {L^2})}^2} - 4{x^2}{L^2}} ]\\ {\rm{s}}{{\rm{h}}^2}\xi {\rm{ = }}\frac{1}{{2{L^2}}}[{x^2} + {y^2} - {L^2} + \sqrt {{{({x^2} + {y^2} + {L^2})}^2} - 4{x^2}{L^2}} ]\\ {\cos ^2}\eta {\rm{ = }}\frac{1}{{2{L^2}}}[{x^2} + {y^2} + {L^2} - \sqrt {{{({x^2} + {y^2} + {L^2})}^2} - 4{x^2}{L^2}} ]\\ {\sin ^2}\eta {\rm{ = }}\frac{1}{{2{L^2}}}[ - {x^2} - {y^2} + {L^2} + \sqrt {{{({x^2} + {y^2} + {L^2})}^2} - 4{x^2}{L^2}} ] \end{array} $ | (4) |
由式(4)映射后,上半物平面Z变为像平面W上宽度为π的区域,水平井位于η轴0到π之间,为排油坑道。直井坐标为
| $ \{ _{{\eta _0} = \arctan (\sqrt {{B_0}} + \sqrt {1 - {B_0}} )}^{{\xi _0} = \ln \sqrt {{A_0}} + \sqrt {{A_0} - 1} } $ | (5) |
其中:A0 =
物平面Z上相应的(x,y)通过式(4)可反映形成像平面W(图 3)。

|
下载原图 图 3 加密水平井基础注采井组像平面W示意图 Fig. 3 Schematic diagram of W image plane of basic injec‐ tion-production well group of infilled horizontal wells |
以像平面W上φ(ξ0, η0) 处的直井注水井为例(其余井同理可得),由镜像反映法,可以映射形成一列注水井、一列生产井共同生产的情形(图 4)。

|
下载原图 图 4 镜像反映法示意图 Fig. 4 Schematic diagram of mirror reflection method |
(ξ0, η0)处注水井在像平面W上由镜像反映法映射出的无限注水井排,其坐标可归纳为
第1类:(ξ0, η0 + 2nπ),n = 0,±1,±2…。
第2类:(ξ0, -η0 + 2nπ),n = 0,±1,±2…。
映射出的无限采油井排坐标依次归纳为
第1类:(-ξ0, η0 + 2nπ),n = 0,±1,±2…。
第2类:(-ξ0, -η0 + 2nπ),n = 0,±1,±2…。
2.1.2 像平面W中势的求解根据无限大地层平面中任一点势的表达式
| $ \varphi = \frac{q}{{2\pi }}\ln \sqrt {{{(x - {x_0})}^2} + {{(y - {y_0})}^2}} + C $ | (6) |
其中:
式中:x0,y0表示点源或点汇的坐标;Q为点源的注入量或点汇的产出量,m3/d;h为储层厚度,m。
通过式(6)及势的叠加原理,将平面上各点源或点汇产生的势进行叠加,可得(ξ0, η0)处注水井在任一点产生的势为
| $ \begin{array}{*{20}{c}} {\varphi = \frac{q}{{4\pi }}\sum\limits_{ - \infty }^{ + \infty } {\left\{ {\ln \frac{{{{(\xi + {\xi _0})}^2} + {{[\eta - ({\eta _0} + 2n\pi )]}^2}}}{{{{(\xi - {\xi _0})}^2} + {{[\eta - ({\eta _0} + 2n\pi )]}^2}}} + } \right.} }\\ {\left. {\ln \frac{{{{(\xi + {\xi _0})}^2} + {{[\eta - ( - {\eta _0} + 2n\pi )]}^2}}}{{{{(\xi - {\xi _0})}^2} + {{[\eta - ( - {\eta _0} + 2n\pi )]}^2}}}} \right\}} \end{array} $ | (7) |
利用贝塞尔公式,得到下式
| $ \begin{array}{*{20}{c}} {\sum\limits_{ - \infty }^{ + \infty } {\ln [{{(x - {x_1})}^2} + {{(y - nh - {y_1})}^2}] = } }\\ {\ln [{\rm{ch}}\frac{{2\pi (x - {x_1})}}{h} - \cos \frac{{2\pi (y - {y_1})}}{h}]} \end{array} $ | (8) |
可将式(7)无穷和的式化简为
| $ \begin{array}{*{20}{c}} {{\varphi _{\rm I}} = \frac{q}{{4\pi }}[\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) - \cos (\eta - {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) - \cos (\eta - {\eta _0})}} + }\\ {\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) - \cos (\eta + {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) - \cos (\eta + {\eta _0})}}]} \end{array} $ | (9) |
根据上述方法,同理可得像平面W上(ξ0, π - η0)处注水井的势为
| $ \begin{array}{*{20}{c}} {{\varphi _\parallel } = \frac{q}{{4\pi }}[\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) + \cos (\eta + {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) + \cos (\eta + {\eta _0})}} + }\\ {\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) + \cos (\eta - {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) + \cos (\eta - {\eta _0})}}]} \end{array} $ | (10) |
由式(9)和式(10)通过势叠加可以得到该注采单元在像平面W中任一点产生的势为
| $ \begin{array}{*{20}{c}} {\varphi = \frac{q}{{4\pi }}[\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) - \cos (\eta - {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) - \cos (\eta - {\eta _0})}} \bullet \frac{{{\rm{ch}}(\xi - {\xi _0}) - \cos (\eta + {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) - \cos (\eta + {\eta _0})}}] + }\\ {\frac{q}{{4\pi }}[\ln \frac{{{\rm{ch}}(\xi - {\xi _0}) + \cos (\eta + {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) + \cos (\eta + {\eta _0})}} \bullet \frac{{{\rm{ch}}(\xi - {\xi _0}) + \cos (\eta - {\eta _0})}}{{{\rm{ch}}(\xi + {\xi _0}) + \cos (\eta - {\eta _0})}}]} \end{array} $ | (11) |
基于式(11),根据物平面Z与像平面W之间的坐标对应关系,将像平面W上的位置反演到物平面Z上,即可得到该注采井组在物平面Z上任一点产生的势。
2.2 注采单元中流函数的求解
基于任一点的势函数(式11),结合柯西-黎曼条件(
| $ \psi = \frac{q}{{4\pi }}\left\{ {\begin{array}{*{20}{c}} {\frac{{2{\rm{sh}}(\xi + {\xi _0})\arctan [\frac{{\tan \frac{{\eta - {\eta _0}}}{2}\left| {{\rm{sh(}}\xi {\rm{ + }}{\xi _0})} \right|}}{{{\rm{ch(}}\xi {\rm{ + }}{\xi _{\rm{0}}}{\rm{) + 1}}}}]}}{{\left| {{\rm{sh}}(\xi + {\xi _0})} \right|}} + \frac{{2{\rm{sh}}(\xi + {\xi _0})\arctan [\frac{{\tan \frac{{\eta - {\eta _0}}}{2}\left| {{\rm{sh(}}\xi {\rm{ + }}{\xi _0})} \right|}}{{{\rm{ch(}}\xi {\rm{ + }}{\xi _{\rm{0}}}{\rm{) - 1}}}}]}}{{\left| {{\rm{sh}}(\xi + {\xi _0})} \right|}}}\\ { + \frac{{2{\rm{sh}}(\xi + {\xi _0})\arctan [\frac{{\tan \frac{{\eta + {\eta _0}}}{2}\left| {{\rm{sh(}}\xi {\rm{ + }}{\xi _0})} \right|}}{{{\rm{ch(}}\xi {\rm{ + }}{\xi _{\rm{0}}}{\rm{) + 1}}}}]}}{{\left| {{\rm{sh}}(\xi + {\xi _0})} \right|}} + \frac{{2{\rm{sh}}(\xi + {\xi _0})\arctan [\frac{{\tan \frac{{\eta - {\eta _0}}}{2}\left| {{\rm{sh(}}\xi {\rm{ + }}{\xi _0})} \right|}}{{{\rm{ch(}}\xi {\rm{ + }}{\xi _{\rm{0}}}{\rm{) - 1}}}}]}}{{\left| {{\rm{sh}}(\xi + {\xi _0})} \right|}}}\\ { - \frac{{2{\rm{sh}}(\xi - {\xi _0})\arctan [\frac{{\tan \frac{{\eta - {\eta _0}}}{2}\left| {{\rm{sh(}}\xi - {\xi _0})} \right|}}{{{\rm{ch(}}\xi - {\xi _{\rm{0}}}{\rm{) + 1}}}}]}}{{\left| {{\rm{sh}}(\xi - {\xi _0})} \right|}} - \frac{{2{\rm{sh}}(\xi - {\xi _0})\arctan [\frac{{\tan \frac{{\eta - {\eta _0}}}{2}\left| {{\rm{sh(}}\xi - {\xi _0})} \right|}}{{{\rm{ch(}}\xi - {\xi _{\rm{0}}}{\rm{) - 1}}}}]}}{{\left| {{\rm{sh}}(\xi - {\xi _0})} \right|}}}\\ { - \frac{{2{\rm{sh}}(\xi - {\xi _0})\arctan [\frac{{\tan \frac{{\eta + {\eta _0}}}{2}\left| {{\rm{sh(}}\xi - {\xi _0})} \right|}}{{{\rm{ch(}}\xi - {\xi _{\rm{0}}}{\rm{) + 1}}}}]}}{{\left| {{\rm{sh}}(\xi - {\xi _0})} \right|}} - \frac{{2{\rm{sh}}(\xi - {\xi _0})\arctan [\frac{{\tan \frac{{\eta + {\eta _0}}}{2}\left| {{\rm{sh(}}\xi - {\xi _0})} \right|}}{{{\rm{ch(}}\xi - {\xi _{\rm{0}}}{\rm{) - 1}}}}]}}{{\left| {{\rm{sh}}(\xi - {\xi _0})} \right|}}} \end{array}} \right\} $ | (12) |
利用前述方法,可以计算典型注采井网中渗流场的分布,分析不同条件下注采单元储量单元规律,为确定合理调整方式奠定基础。
3 注采单元中渗流场变化规律分析方法 3.1 储量有效动用能力的表征方法通过渗流模型求解得到注采单元中势的分布(势函数φ),根据势与压力的关系,可求得平面任一点压力p(i,j),基本关系式为
| $ {\rm{d}}\varphi = \frac{K}{\mu }{\rm{d}}p $ | (13) |
定义平面x方向上、y方向上的压力梯度分别为∇px,∇py
| $ \nabla {P_x} = \frac{{p(i, j) - p(i, j - 1)}}{{dx}}, i = 1, 2, \cdots N;j = 2, 3, \cdots , N $ | (14) |
| $ \nabla {P_y} = \frac{{p(i, j) - p(i - 1, j)}}{{dy}}, i = 2, 3, \cdots N;j = 1, 2, \cdots , N $ | (15) |
∇px,∇py的大小由上式计算所得,方向分别为x轴方向与y轴方向。可以得到总驱动压力梯度∇p大小为
| $ \nabla P = \sqrt {\nabla {P_x}^2 + \nabla {P_y}^2} $ | (16) |
流体在均质、等厚地层水平面上任意点处的渗流速度为
| $ v = - \frac{K}{\mu }\nabla P $ | (17) |
流体渗流速度大小反映了该位置流体的流动能力和储量有效动用程度,流体渗流速度大于0,表示该位置储量得到动用;流动速度越大,储量动用程度就越高。由于流体渗流速度大小与该处流体的压力梯度大小成正比,因此可以用总驱动压力梯度大小来反映储层中储量的动用情况。某一位置的驱动压力梯度越大,该位置流体越易流动,储量动用能力越好。
3.2 储量动用效果的评价方法根据以上分析,可以用注采单元中驱动压力梯度分布和占有范围,来评价储量动用效果。
在图 1所示的整个注采单元中,设单元控制面积为Ao。驱动压力梯度大于等于某一值∇pk时,其等值线包络的动用范围为Apk。
为统一对比分析,定义“无因次动用范围D pk”表征储量有效动用程度,表达式为
| $ {D_{pk}} = \frac{{{A_{pk}}}}{{{A_0}}}, 0 < {D_{pk}} \le 1 $ | (18) |
无因次动用范围D pk值越大,表示大于该驱动条件下的储量动用范围越大,反映注采单元中的储量动用程度越好。可以根据注采井网单元的渗流场分布情况,绘制无因次动用范围与驱动压力梯度的关系曲线,分析注采井网的储量有效动用情况。
定义“无因次动用强度TD”表征注采井网单元中整体储量有效动用效果,表达式为
| $ {T_{\rm{D}}} = \sum {D_{pk}} \times \nabla {P_k} $ | (19) |
无因次动用强度TD值越大,表示该条件下单位无因次面积内的驱动力越大,注采单元中的储量动用效果越好。可以根据渗流场分布,绘制出不同条件下无因次动用强度TD的变化曲线,分析不同因素对储量有效动用效果的影响。
4 注采单元中渗流场分布变化规律基于渤海HD油田特点和开发状况,利用储量动用能力及动用效果评价指标,分析不同条件下注采井网渗流场分布变化,为确定注采井网合理加密调整策略奠定理论基础。
4.1 加密水平井对注采单元渗流场的影响基本参数取值为:350 m×350 m的反九点基础井网,水平井长度2 L=200 m(对比条件初值),储层中方向渗透率Kx/Ky=1,加密水平井的产液能力初定为原直井采油井的2.0倍,在注采井网单元中保持整体注采平衡。
基于前述方法,计算得到基础反九点注采单元渗流场分布[图 5(a)]、驱动压力梯度分布[图 5(b)] 及水平井加密后的组合井网注采单元渗流场分布[图 5(c)]、驱动压力梯度分布[图 5(d)]。
|
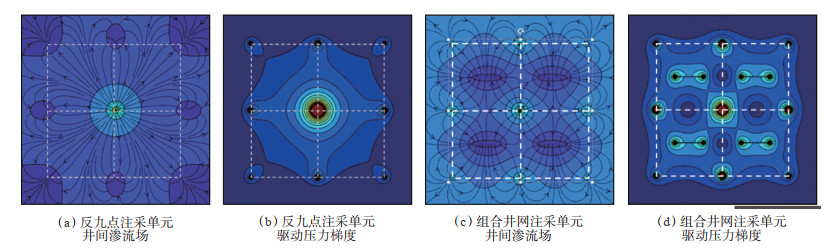
下载原图 图 5 加密水平井前后注采井网单元渗流场变化 Fig. 5 Seepage field changes of injection-production well pattern unit of infilled horizontal wells |
井间渗流场分布图中,蓝色越浅代表该位置势越大,蓝水越深,该处势越小;流线箭头方向为液流方向,流线密集程度越高,该处流速越大、流动能力越强;井间驱动压力梯度分布图中,蓝色越深反映该位置压力梯度越小,红色越深反映该位置压力梯度越大。
对比不同井网单元的渗流场及驱动压力梯度分布可见:①基础反九点直井井网在对角注采井连线上驱动相对较慢,井间储量动用较弱。②加密水平井部署后,流线由中心向四周发散,被“吸引”集中于井间对角区域,体现水平井对该区域的引流作用,注采实现了液流改向。③在加密水平井后的驱动压力梯度图中,水平井附近呈现出高驱动压力梯度条带,有效动用了原基础中弱动用的区域,同时整个井网单元注采强度也有显著提高。
4.2 储层各向异性对水平井加密效果的影响为分析加密水平井形成组合井网的适应性,在其它参数取值相同的条件下,计算对比不同储层各向异性注采单元渗流场,并统计分析储层各向异性对储量动用效果的影响。
对比图 5中Kx/Ky=1,在相同的注采条件下,分别计算:主渗流方向为Kx,且Kx/Ky=5;主渗流方向为Ky,且Kx/Ky=0.2。注采单元渗流场分布及驱动压力梯度图如图 6所示。
|
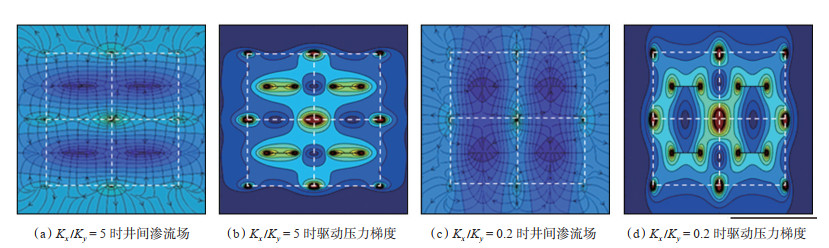
下载原图 图 6 不同储层非均质条件下渗流场变化 Fig. 6 Seepage field changes under different reservoir heterogeneity |
从图 6中可看出:与Kx/Ky=1各向同性下的驱动压力梯度分布相比,储层具有各向异性时井网驱动压力梯度分布范围明显增大,水平井加密井网具有较好的适应性;当Kx/Ky=5,水平井平行于主渗流Kx方向时,注采井间线性驱替范围更大,驱替效果更好。
不同条件下,注采井网单元中储量动用范围变化、储量动用效果变化曲线见图 7。
|
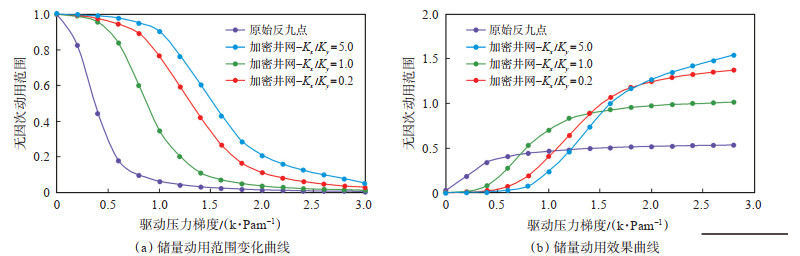
下载原图 图 7 渗透率各向异性对水平井加密效果的影响 Fig. 7 Influence of permeability anisotropy on the effect of horizontal well infilling |
由图 7可以看出:与反九点基础井网相比,水平井加密后,在相同驱动压力梯度范围内,组合井网注采单元中的无因次动用范围、无因次动用强度都明显增大,注采单元储量有效动用能力及效果都得到一定程度的提高。当存在渗透率各向异性,加密水平井的方位与主渗流方向Kx一致时,储量动用效果提高幅度最大。
5 渤海HD油田水平井加密合理技术策略 5.1 加密水平井合理长度基于以上建立的注采单元储量动用效果分析评价方法,定量研究基于典型反九点井网加密水平井方式下,注采加密调整的关键参数技术界限——合理水平井长度。
根据油田开发经验和相关理论认识,加密水平井长度需同时考虑油田产量、避免井间干扰和过早见水的要求。实际基础井网为350 m×350 m正方形反九点注采井网,加密水平井长度不应超过原始基础井网的井距。
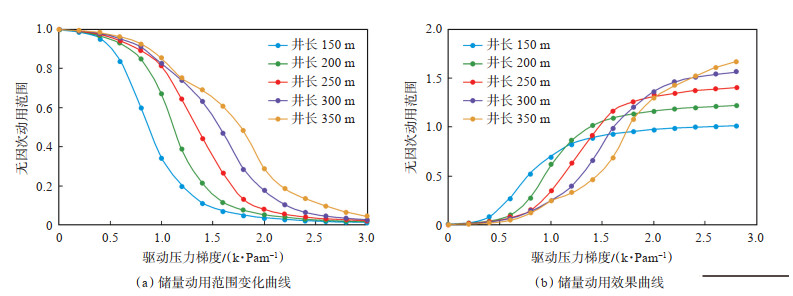
取水平井长度分别为150 m,200 m,250 m,300 m,350 m。在同样生产条件下,保持整体注采平衡,计算不同水平井长度下注采单元渗流场和储量动用变化。绘制不同水平井长度下的注采单元中驱动压力梯度图,以水平井长150 m,300 m为例进行对比(图 8);统计不同水平井长度下无因次动用范围[图 9(a)],计算无因次动用强度[图 9(b)],分析注采单元储量动用效果。
|
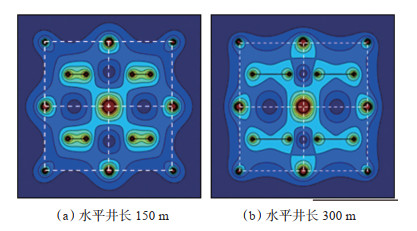
下载原图 图 8 不同水平井长度下驱动压力梯度分布图 Fig. 8 Driving pressure gradient distribution under different horizontal well lengths |
|
下载原图 图 9 水平井长度对水平井加密效果的影响 Fig. 9 Influence of horizontal well length on the effect of horizontal well infilling |
由图 8、图 9可以看出:①在注采井网单元渗流场中,水平井长度越长,原井间内部弱动用区域处提高储量动用能力的范围越大,显著增加注采井网单元的储量动用程度;随着水平井长度的增加,与周围直井的相互干扰程度相应增大。②随着水平井长度的增大,在相同驱动压力梯度下,无因次动用范围越大,当水平井长度超过250 m时,增加趋势减缓,综合考虑生产成本、产量需求及驱替效果,合理水平井长度为250~300 m,约为原井网井距的0.75倍。
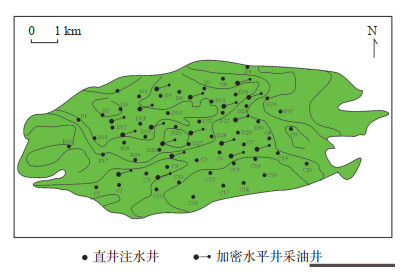
5.2 油田实际应用效果针对渤海HD油田,由基础反九点直井井网开发调整为”直井注-水平井采”的组合井网开发,在原直井基础上,整体加密水平井,通过直井转注等综合调整,形成交错的注采井数比约为1∶1的强化注采井网(图 10)。
|
下载原图 图 10 渤海HD油田开发井网调整部署图 Fig. 10 Well pattern adjustment and deployment for HD oilfield in Bohai Sea |
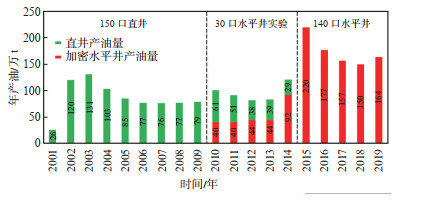
油田在2010年进行了30口水平井加密部署试验,注采井网整体调整效果较好,油田年产油量明显提升(图 11),2015年产量创历史新高,油田采油速度由0.8% 提高至1.8%,预测水驱采收率提高了10.1%,开发效果提升显著。
|
下载原图 图 11 渤海HD油田开发动态变化图 Fig. 11 Dynamic changes of HD oilfield development in Bohai Sea |
1)基于渤海HD油田基础参数及其典型反九点注采井网模式,建立了井间内部整体加密水平井的组合井网渗流模型,可以定量计算不同条件下组合井网注采单元的渗流场分布变化,直观反映井间储量动用情况。
(2)建立了注采井网单元储量动用效果的评价方法,深入认识加密水平井对改变直井反九点注采井网渗流场的作用及加密调整后注采井网单元中的储量动用变化规律。研究表明水平井加密后,储量有效动用能力及效果都得到一定程度提高;当存在渗透率各向异性,加密水平井的方位与主渗流方向Kx一致时,储量动用效果提高幅度最大。
(3)结合渤海HD油田实际,综合储量动用效果和开发实施条件,确定了基础反九点注采井网整体加密水平井的关键技术策略,合理水平井长度为250~300 m,约为原井网井距的0.75倍。
| [1] |
赵春森. 水平井与直井整体开发渗流理论研究. 大庆: 大庆石油学院, 2001. ZHAO C S. Theoretical study on seepage flow in horizontal and vertical wells. Daqing: Daqing Petroleum Institute, 2001. |
| [2] |
叶双江, 姜汉桥, 李俊键, 等. 混合井网条件下加密井产能计算模型及应用. 计算物理, 2011, 28(5): 693-697. YE S J, JIANG H Q, LI J J, et al. Model and application of infill well productivity calculation under mixed well pattern. Computational Physics, 2011, 28(5): 693-697. DOI:10.3969/j.issn.1001-246X.2011.05.008 |
| [3] |
付莹. 基于流管法平-直联合开发井网水平井开发规律研究. 大庆: 东北石油大学, 2016. FU Y. Research on the development law of horizontal wells based on the flow-pipe method flat-straight joint development well pattern. Daqing: Northeast Petroleum University, 2016. |
| [4] |
郎兆新, 张丽华, 程林松, 等. 水平井与直井联合开采问题: 五点法面积井网. 石油大学学报(自然科学版), 1993(6): 50-55. LANG Z X, ZHANG L H, CHENG L S, et al. Joint mining problem between horizontal well and vertical well: 5-point area well network. Journal of the University of Petroleum(Natural Science Edition), 1993(6): 50-55. |
| [5] |
葛家理, 王德民, 曲德斌. 水平井与直井联合面积布井的开发理论研究(二): 七点法面积井网. 石油勘探与开发, 1995(2): 47-50. GE J L, WANG D M, QU D B. Theoretical study on the development of combined wells with horizontal and vertical wells (2): Seven-point method area well pattern. Petroleum Exploration and Development, 1995(2): 47-50. DOI:10.3321/j.issn:1000-0747.1995.02.008 |
| [6] |
陈民锋, 王兆琪, 张琪琛, 等. 启动压力影响下注采井间有效驱替规律. 深圳大学学报(理工版), 2017, 34(1): 91-97. CHEN M F, WANG Z Q, ZHANG Q C, et al. Law of effective displacement between injection and production wells under the influence of starting pressure. Journal of Shenzhen University (Science and Technology Edition), 2017, 34(1): 91-97. |
| [7] |
COLLINS D A, NGHIEM L X, AGARWAL R K, et al. Field-scale simulation of horizontal wells with hybrid grids. SPE 21218, 1991. |
| [8] |
CHODZICKI J D. Horizontal well infill development of the Manor Spearfish Field. Journal of Canadian Petroleum Technology, 2005, 44(11): 51-55. |
| [9] |
刘月田. 水平井整体井网渗流解析解. 石油勘探与开发, 2001(3): 57-59. LIU Y T. Analytical solution of seepage flow in horizontal wells. Petroleum Exploration and Development, 2001(3): 57-59. DOI:10.3321/j.issn:1000-0747.2001.03.016 |
| [10] |
罗万静. 混合井网渗流理论及优化布井. 北京: 中国地质大学(北京), 2009. LUO W J. Theory of mixed well pattern seepage and optimization of well layout. Beijing: China University of Geosciences(Beijing), 2009. |
| [11] |
叶双江, 陈志海, 姜汉桥, 等. 水平井与直井混合注采井网的流场计算: 以五点法注采井网为例. 计算物理, 2017, 34(4): 437-444. YE S J, CHEN Z H, JIANG H Q, et al. Flow field calculation of the mixed injection-production well pattern of horizontal and vertical wells: Taking the five-point injection-production well pattern as an example. Computational Physics, 2017, 34(4): 437-444. DOI:10.3969/j.issn.1001-246X.2017.04.009 |
| [12] |
刘月田. 水平井整体井网渗流解析解. 石油勘探与开发, 2001(3): 57-59. LIU Y T. Analytical solution of seepage flow in horizontal well pattern. Petroleum Exploration and Development, 2001(3): 57-59. DOI:10.3321/j.issn:1000-0747.2001.03.016 |
| [13] |
李传亮, 朱苏阳, 柴改建, 等. 直井与水平井的产能对比. 岩性油气藏, 2018, 30(3): 12-16. LI C L, ZHU S Y, CHAI G J, et al. Comparison of production capacity between vertical and horizontal wells. Lithologic Reservoirs, 2018, 30(3): 12-16. |
| [14] |
陈民锋, 赵晶, 张贤松, 等. 低渗透稠油油藏水平井极限动用范围. 中国石油大学学报(自然科学版), 2014, 38(2): 103-108. CHEN M F, ZHAO J, ZHANG X S, et al. The limit production range of horizontal wells in low-permeability heavy oil reservoirs. Journal of China University of Petroleum(Edition of Natural Science), 2014, 38(2): 103-108. DOI:10.3969/j.issn.1673-5005.2014.02.016 |
| [15] |
范子菲, 方宏长, 俞国凡. 水平井水平段最优长度设计方法研究. 石油学报, 1997(1): 57-64. FAN Z F, FANG H C, YU G F. Study on the optimal length design method of horizontal well horizontal section. Acta Petrolei Sinica, 1997(1): 57-64. |
| [16] |
凌宗发, 胡永乐, 李保柱, 等. 水平井注采井网优化. 石油勘探与开发, 2007(1): 65-72. LING Z F, HU Y L, LI B Z, et al. Optimization of horizontal well injection and production wells. Petroleum Exploration and Development, 2007(1): 65-72. DOI:10.3321/j.issn:1000-0747.2007.01.013 |
| [17] |
刘明明, 王全, 马收, 等. 基于混合粒子群算法的煤层气井位优化方法. 岩性油气藏, 2020, 32(6): 164-171. LIU M M, WANG Q, MA S, et al. A method of coalbed methane well location optimization based on hybrid particle swarm optimization. Lithologic Reservoirs, 2020, 32(6): 164-171. |
| [18] |
陈元千, 邹存友. 考虑各向异性和偏心距影响的水平井产量公式推导、对比与应用. 新疆石油地质, 2009, 30(4): 486-489. CHEN Y Q, ZOU C Y. Derivation, comparison and application of horizontal well production formula considering the effects of anisotropy and eccentricity. Xinjiang Petroleum Geology, 2009, 30(4): 486-489. |
| [19] |
周洪亮, 尹洪军, 李美芳, 等. 各向异性油藏水平井井网渗流场分析. 特种油气藏, 2010, 17(1): 81-84. ZHOU H L, YIN H J, LI M F, et al. Analysis of seepage field of horizontal well pattern in anisotropic reservoir. Special Oil and Gas Reservoirs, 2010, 17(1): 81-84. DOI:10.3969/j.issn.1006-6535.2010.01.022 |
| [20] |
陈民锋, 盖建, 王敏, 等. 普通稠油油藏水驱开发有效注采井距的确定. 中国海上油气, 2014, 26(4): 50-53. CHEN M F, GAI J, WANG M, et al. Determination of effective injection-production well spacing for water drive development of ordinary heavy oil reservoirs. China Offshore Oil & Gas, 2014, 26(4): 50-53. |
| [21] |
陈民锋, 尹承哲, 王振鹏, 等. 直井-水平井组合井网平面井间动用规律. 深圳大学学报(理工版), 2018, 35(4): 368-376. CHEN M F, YIN C Z, WANG Z P, et al. Vertical well-horizontal well combination well pattern horizontal inter-well production law. Journal of Shenzhen University(Science and Technology Edition), 2018, 35(4): 368-376. |
 2021, Vol. 33
2021, Vol. 33




