曲流河砂体储层作为重要的陆相碎屑岩储层类型之一，具有“蚀凹增凸”的特点，横向变化快，非均质性强，采收率较低，在我国中新生代含油气盆地中占有较大的比例^[1-2]。点坝砂体是曲流河储层的重要研究对象，曲流河的几何形态演变特征与点坝砂体定量表征的研究一直备受关注，且逐渐由定性描述向多元定量化表征方向转变^[3]。早在20世纪60年代，Schumm^[4]对北美大平原上的50个单河道段进行划分，建立了曲率与河道宽深比的关系模式；Leopold^[5]探讨了河道宽度与河弯跨度间的关系模式。20世纪70 —80年代，Schumm^[6]对澳大利亚36条河流的点坝砂体进行了分析，讨论了河道深度、侧积体厚度、宽度以及曲率等参数的定量关系；Lorenz等^[7]总结出单一曲流带与河道宽度的关系模式。进入21世纪，Nicoll等^[8]的研究表明，在河湾平面几何形态上，限制性河湾与自由河湾较为一致，但在形态参数方面不同；岳大力等^[9]、李宇鹏等^[10]、石书缘等^[11]、范广娟等^[12]对点坝砂体规模与河流满岸宽度之间的关系进行了总结，针对不同地区河流点坝砂体规模进行了定量表征；王海峰等^[13]利用储层构型理论的分级表征思路，明确了不同级次的砂体或界面规模的定量关系。此外，石书缘等^[11]、Leeder^[14]、刘振坤等^[15]、乔辉等^[16]、王冬冬等^[17]针对不同曲率条件下点坝砂体规模的定量参数关系也进行了大量的研究，但对差异曲率范围下点坝砂体规模参数的定量关系研究结果尚不统一。就研究方法而言，曲流河砂体储层的研究通常使用密井网解剖、露头解剖与现代沉积解剖等方法^[18-23]。密井网解剖适用于井网密度较大的情况，露头解剖对露头出露的要求较高，现代沉积解剖局限于单剖面的建立。定量表征方法适用范围广，能对河流几何形态及沉积单元进行宏观的了解及定量化表征。总体上，对于河流砂体储层的表征已经成为研究热点，但对单体河流沉积单元进行划分的研究则较为缺乏。

选取黄河源区现代白河作为研究对象，基于ArcGIS 10.6软件对白河流域遥感影像进行预处理及矢量化，识别白河流域31个典型点坝砂体并进行测量，通过坡降、曲率等指标对白河进行分段和精细刻画，分析点坝砂体规模参数的基础测量数据，进而明确不同曲流段河道宽度与点坝砂体规模之间的关系，以期为合理建立曲流河点坝砂体储层和准确预测剩余油分布提供依据。

白河流域位于黄河源区的东南部，起源于巴颜喀拉山东端的查勒肯地区，由南向北流经安曲、邛溪、瓦切，至若尔盖县西南部的唐克镇附近汇入黄河（图 1）。白河源头海拔高程约4 460 m，沿岸沼泽泥炭发育较弱，河水较为清澈。干流全长约270 km，流域面积为5 488 km²，平均比降3.8‰，其中大部分河段在0.5‰以下，大于1‰的河段仅占1/5^[24]。白河是自然发育的曲流河，植被发育较好，河道几何形态呈蜿蜒曲折状，成为定量化研究弯曲河流点坝砂体规模的理想对象。白河地处特提斯—喜马拉雅构造域，故新构造运动十分强烈^[25]。上游两侧为丘陵地貌，中游地形趋缓，下游进入因青藏高原隆起而形成的若尔盖盆地^[26]，整体上，上游形成狭长的直线状河谷，中下游形成宽阔的线性河谷，白河冲积平原面积由小变大。

图 1

Fig. 1

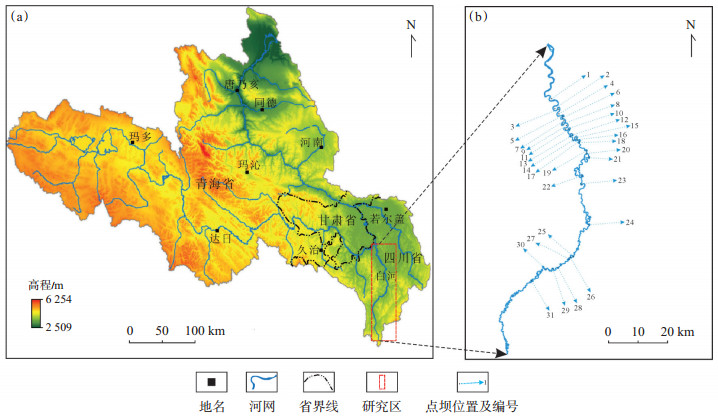
下载原图 图 1 黄河源区白河位置[27]（a）及点坝分布图（b） Fig. 1 Location of Baihe river(a)and distribution of point bars(b)in Yellow River source area

曲流河发育点坝（边滩）、牛轭湖、天然堤、决口扇、河漫滩等沉积单元。其中，点坝与牛轭湖对曲流河储层具有重要意义。白河有圆弧形、长条形、U形和微弯形点坝，沿程点坝形状趋于规则^[28]；有Ω型、U型和月牙型牛轭湖，其中月牙型牛轭湖数量最多，U型次之，Ω型数量最少，沿程牛轭湖数量呈现由多变少的趋势^[29-30]。从前人研究结果得知白河河道宽度与河谷宽度沿程具有正相关关系^[29]。

黄河源区白河流域遥感影像数据来源于91卫图助手，分辨率为2 m。ArcGIS软件具有地理信息处理能力强、数据存储空间大及平面展示效果佳等优点^[31]，在定量表征点坝砂体规模上，ArcGIS软件极大地提高了工作效率，且提升了成果质量。为了明确点坝砂体规模与不同曲率河道宽度的关系，此次研究基于高分辨率遥感影像，选择黄河源区白河流域单个分辨率较高的点坝砂体，通过ArcGIS 10.6软件进行矢量化，测量了31个典型点坝砂体相关参数（表 1），测量数据包括3个部分：①曲流段的曲率（曲率k =河道曲线长度L_c/河谷直线长度L_v）；②曲流段点坝长度（L_p）与点坝宽度（W_p）；③曲流段河道宽度（W_r）。从所得出的基础测量数据表可以看出，在进行最小二乘法拟合分析的基础上，可探究白河点坝长度与点坝宽度、点坝长度与河道宽度、点坝宽度与河道宽度的关系方程。

表 1(Table 1)

表 1 黄河源区白河点坝砂体的测量数据 Table 1 Measurement data of point bar sand bodies in Baihe river of Yellow River source area 点坝编号 Wr/m Lp/m Wp/m Lc/m Lv/m k 1 226 1 257 690 2 026 1 375 1.47 2 272 1 077 1 281 3 045 1 442 2.11 3 133 864 636 2 800 965 2.90 4 214 1 673 1 396 3 373 1 644 2.05 5 168 380 366 1 384 518 2.67 6 165 738 690 1 801 744 2.42 7 164 971 842 2 416 1 050 2.30 8 177 263 1 044 2 231 776 2.88 9 180 1 154 1 159 3 344 1 345 2.49 10 159 674 990 2 640 1 088 2.43 11 142 473 414 1 903 471 4.04 12 167 493 645 1 718 539 3.19 13 113 505 555 1 336 597 2.24 14 117 573 742 1 968 828 2.38 15 138 511 911 2 063 707 2.92 16 156 581 807 1 791 732 2.45 17 141 408 462 1 425 627 2.27 18 127 496 298 1 010 610 1.66 19 116 739 431 871 595 1.46 20 115 630 303 712 547 1.30 21 64 507 491 1 248 672 1.86 22 130 728 511 1 317 918 1.43 23 96 592 503 1 389 667 2.08 24 74 687 513 849 585 1.45 25 101 417 383 920 511 1.80 26 76 429 451 994 513 1.94 27 85 275 225 677 357 1.90 28 116 370 149 540 369 1.46 29 101 465 355 1 102 594 1.86 30 110 580 346 943 617 1.53 31 93 345 234 707 364 1.94

下载CSV 表 1 黄河源区白河点坝砂体的测量数据 Table 1 Measurement data of point bar sand bodies in Baihe river of Yellow River source area

在ArcGIS软件中，空间数据分析与处理可将遥感影像、航空相片、现有的地图等转成计算机可以识别处理的数字形式^[32]。对于现代曲流河的研究而言，可将河道单元参数矢量化并进行分析。在建立白河点坝砂体定量化测量数据表的过程中，此次研究采用的测量流程为：

（1）导入遥感卫星图。将分辨率为2 m的遥感影像导入ArcGIS 10.6，找出需要测量的点坝砂体。

（2）建立文件地理数据库。在ArcGIS 10.6数据视图状态下，找到ArcCatalog目标树，建立文件地理数据库。

（3）创建要素类。在新建的文件地理数据库上新建要素类，输入名称“点坝长度”，定义其类型为“线要素”，定义其坐标系统为WGS 1984 UTM Zone 48 N，XY容差设置为0.001，确定要素类字段名（“经度”、“纬度”与“点坝长度”）及其类型（“文本”）与属性（长度设置为20字节）。

（4）编辑参数。在编辑器菜单中选择开始编辑，在创建要素栏中选择“点坝长度”要素，沿着点坝长度进行刻画，编辑结束时在编辑器菜单中选择结束编辑。

（5）查看参数属性。在内容列表中，找到“点坝长度”图层，打开点坝长度的属性表，查看点坝长度属性。

根据上述方法，应用ArcGIS 10.6软件可以得到典型曲流段的河道宽度、点坝宽度、河道曲线长度、河谷直线长度等相关数据，形成白河测量数据表，成为白河点坝砂体定量化研究的基础源数据。

从白河的测量数据（表 1）可以看出，河道宽度为64~272 m，在河道宽度为110~120 m时，点坝的数量最多，为6个；点坝长度为263~1 673 m，当点坝长度为408~592 m时，点坝的数量有14个。由此可知，点坝长度集中在408~592 m，且变化幅度较大；点坝宽度为149~1 396 m，呈现波动变化趋势；点坝曲率为1.30~4.04，当曲率为1.30~2.00时，点坝的数量有14个（图 2）。

图 2

Fig. 2

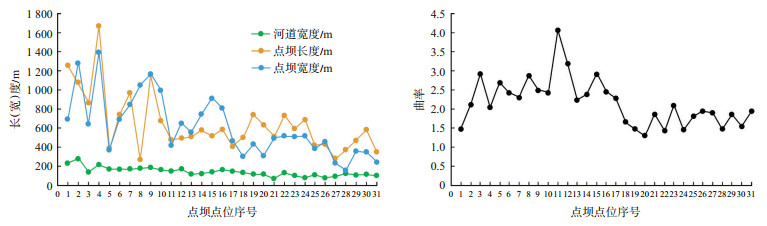
下载原图 图 2 黄河源区白河不同点坝砂体规模参数对比折线图 Fig. 2 Line chart showing parameters comparison of point bar sand body scale in Baihe river of Yellow River source area

通过对黄河源区白河沿程共31个点坝砂体[参见图 1（b）]样本进行对比分析，得出点坝1—10在31个点坝中规模较大，点坝11—24次之，点坝25—31规模最小。白河上游受两侧丘陵限制，河道宽度受地形影响，相对狭窄，水流速度相对较快，河曲弯曲程度较小，在河流凸岸形成规模相对较小的点坝砂体。进入若尔盖盆地后，水流速度降低，河道逐渐变宽，弯曲程度加剧，在河流凸岸形成大型点坝砂体。

在现代冲积河流中，构造条件、相对输沙率、植被条件、气候与沉积物组成等因素影响着河型的空间转化^[33-35]。曲率与坡降也是影响河型变化的因素。此次研究从坡降方面对白河沉积单元进行精细刻画，从曲率方面对白河点坝砂体规模进行定量表征。

河道坡降反映河道沿纵向势能的变化，能表征水动力强弱^[29]。河道坡降与河道宽度、曲流段曲率具有密切的联系。总体来看，坡降越大，则河道宽度越小，曲率越小（图 3）。通过对白河31个曲流段坡降的计算，以0.001为间隔，将坡降划分为0~0.001，0.001~0.002，0.002~0.003，0.003~0.004及0.006~0.007，其中坡降为0~0.001的有23个曲流段、坡降为0.001~0.002的有5个曲流段、坡降为0.002~0.003的有1个曲流段、坡降为0.003~0.004的有1个曲流段、坡降为0.006~0.007的有1个曲流段。在每个区间选择1~2个典型的曲流段进行精细解剖，探寻不同坡降下曲流段沉积单元特征。

图 3

Fig. 3

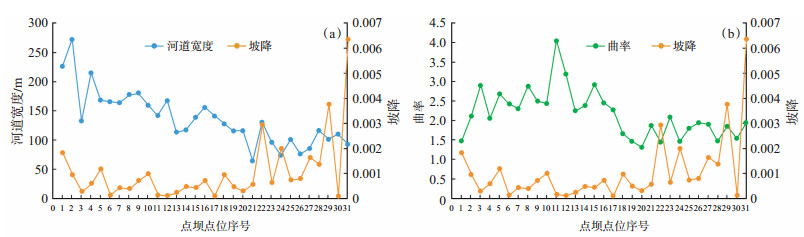
下载原图 图 3 黄河源区白河不同曲流段坡降与河道宽度（a）、曲率（b）关系对比 Fig. 3 Relationships of slope with river channel width(a)and curvature(b)at different meandering sections in Baihe river of Yellow River source area

在坡降为0~0.001的曲流段中，选择点坝2与点坝12所在曲流段进行刻画（图 4，参数如表 1所列）。点坝2所在曲流段的坡降为0.000 94，趋于0.001，河道宽度为272 m，说明河岸抗侵蚀能力较强，曲率为2.11，表明该曲流段的弯曲程度较大；可见呈U型废弃河道，且该废弃河道离主河道有一定距离，说明此处在河流发育较早阶段发生了截弯取直。点坝12所在曲流段的坡降为0.000 09，趋于0，河道宽度为167 m，说明坡降对河道宽度有一定的影响，曲率为3.19，表明该曲流段的弯曲程度大，有废弃河道。点坝2所在曲流段的曲率小于点坝12所在曲流段的曲率，说明坡降大小对曲率具有一定影响。

图 4

Fig. 4

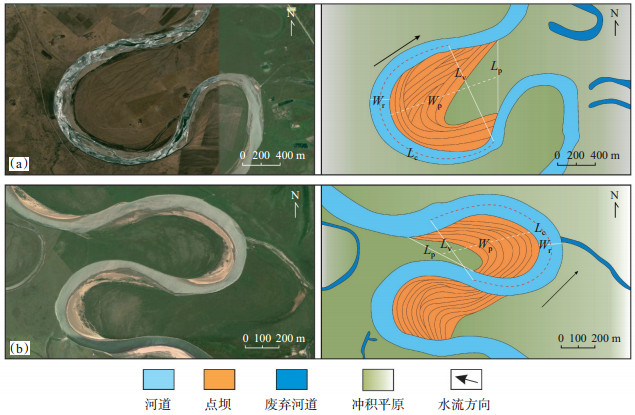
下载原图 图 4 黄河源区白河点坝2（a）和点坝12（b）所在曲流段沉积单元刻画图 Fig. 4 Sedimentary units of meandering sections at point bars 2(a)and 12(b)in Baihe river of Yellow River source area

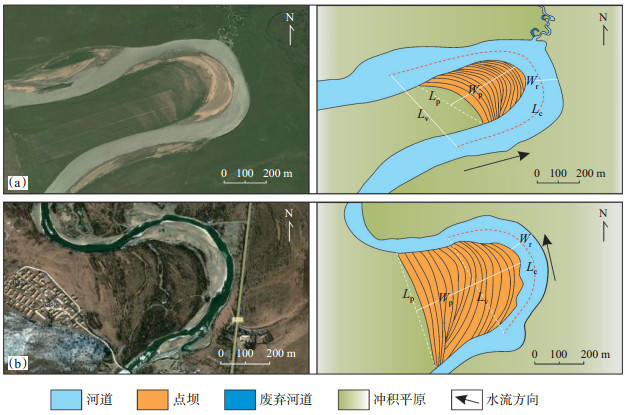
在坡降为0.001~0.002的曲流段中，选择点坝5所在曲流段和点坝24所在曲流段进行刻画（图 5，参数如表 1所列）。点坝5所在曲流段坡降为0.001 2，趋于0.001，河道宽度为168 m，曲率为2.67，说明该曲流段属于高弯曲流段，此外有支流汇入且支流上发育少量U型废弃河道。点坝24所在曲流段坡降为0.002 0，河道宽度为74 m，曲率为1.45，说明该曲流段弯曲程度较低。这2个曲流段的河道宽度差距较大且主河道皆无废弃河道。

图 5

Fig. 5

下载原图 图 5 黄河源区白河点坝5（a）和点坝24（b）所在曲流段沉积单元刻画图 Fig. 5 Sedimentary units of meandering sections at point bars 5(a)and 24(b)in Baihe river of Yellow River source area

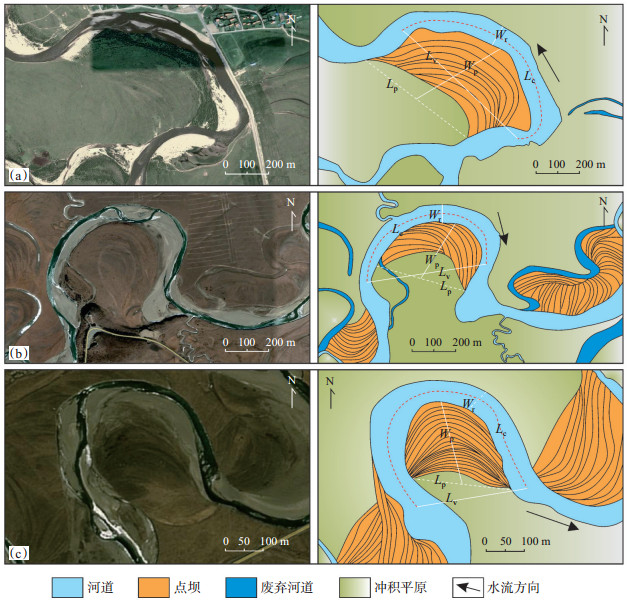
在坡降为0.002~0.003，0.003~0.004和0.006~0.007的曲流段中，分别选择点坝22、点坝29和点坝31所在曲流段进行刻画（图 6，参数如表 1所列）。这3个曲流段的曲率皆小于2.00，河道宽度在31个点坝所在曲流段中均偏小，坡降均偏大。点坝22和点坝29所在曲流段中均有废弃河道，且后者废弃河道数量较多。

图 6

Fig. 6

下载原图 图 6 黄河源区白河点坝22（a）、点坝29（b）、点坝31（c）所在曲流段沉积单元刻画图 Fig. 6 Sedimentary units of meandering sections at point bars 22(a), 29(b)and 31(c)in Baihe river of Yellow River source area

为了明确白河点坝砂体规模与河道宽度的定量关系，基于91卫图助手遥感影像选择并完成了31个点坝砂体规模相关参数的测量。在此基础上通过最小二乘法进行拟合分析，得到对应关系方程和相关系数（图 7）。

图 7

Fig. 7

下载原图 图 7 黄河源区白河点坝砂体规模参数之间的相关关系 Fig. 7 Correlation among parameters of point bar sand bodies in Baihe river of Yellow River source area

统计结果表明，白河的河道宽度与点坝长度、河道宽度与点坝宽度、点坝长度与点坝宽度均呈正相关关系。其中，点坝宽度与河道宽度的相关性最强，点坝长度比河道宽度对点坝宽度的影响小。

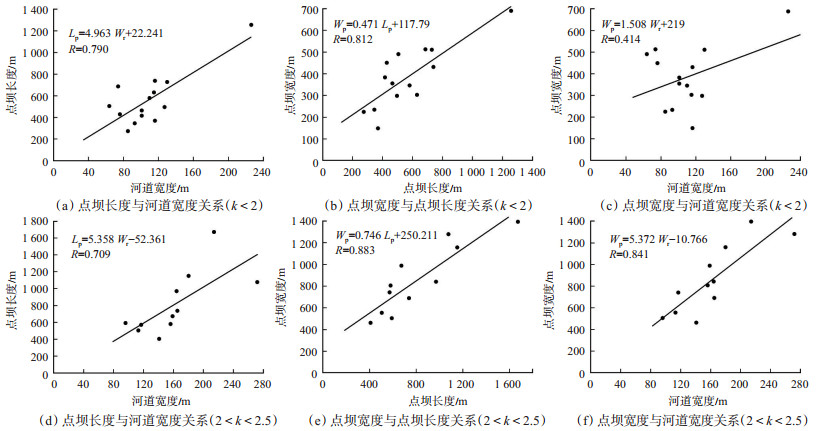
此次研究探讨了河道宽度和点坝砂体规模之间在差异曲率下的定量关系，按k＜2与2＜k＜2.5进行归类，对k＜2的14组数据与2＜k＜2.5的11组数据进行拟合分析，得到对应关系方程和相关系数（图 8）。

图 8

Fig. 8

下载原图 图 8 黄河源区不同曲率范围内白河点坝砂体规模参数之间的相关关系 Fig. 8 Correlation among parameters of point bar sand bodies at different curvature ranges in Baihe river of Yellow River source area

统计结果表明，不同曲率点坝砂体规模与河道宽度之间仍呈正相关关系。当k＜2时，点坝长度与河道宽度的相关系数为0.790，当2＜k＜2.5时，其相关系数为0.709。由此可知，随着曲率的增加，河道宽度与点坝长度相关性相对减弱，表明曲率大小影响点坝的发育程度。当k＜2时，点坝宽度与点坝长度的相关系数为0.812，当2＜k＜2.5时，相关系数为0.883，说明点坝宽度与点坝长度之间的关系受曲率影响相对较小。当k＜2时，点坝宽度与河道宽度的相关系数为0.414，当2＜k＜2.5时，相关系数为0.841，不同曲率下，点坝宽度与河道宽度相关性差异大，且曲率越高，点坝宽度与河道宽度的相关性越好。这也说明通过划分曲率进而研究点坝砂体规模与河道宽度之间的关系是必要的。

点坝砂体是由若干个周期性形成的侧积体叠加而成，在其形成过程中，侧向沉积起主导作用^[36-37]。侧向沉积受来水、来沙及河床边界抗侵蚀能力等因素影响，是由河道内部水流矛盾发展决定的。季节性的洪水事件会导致河道发生迁移或改道，进而形成多期次曲流河点坝砂体^[38]。平原型曲流河坡降相对较小，因此水流速度较小，河曲曲率较大，在河床上会形成规模较大的泥沙淤积体。此次研究选择的点坝1—17的河道宽度为113~272 m，点坝长度为263~1 673 m，点坝宽度为366~1 396 m，曲率为1.47~4.04；点坝18—31的河道宽度为64~130 m，点坝长度为275~739 m，点坝宽度为149~513 m，曲率为1.30~2.08。由此可见，点坝1—17的河道宽度较大，地形平缓，坡降较小，水流流速相对较缓，曲率较大，形成了规模相对较大的点坝砂体；点坝18—31由于受两侧丘陵限制，坡降较大，河宽较小，水流流速相对较急，曲率较小，形成了规模相对较小的点坝砂体。点坝砂体规模是曲流河储层构型研究的重要解剖对象，点坝砂体规模间的定量关系对地下曲流河点坝砂体规模定量表征具有重要作用。

黄河源区现代白河曲流段沉积单元与点坝砂体规模的影响因素多样，本次研究是从坡降划分探讨沉积单元、从曲率划分探讨点坝砂体规模，未从气候、河道深度、物源变化等因素进行深入探讨，可以考虑更多的因素加以深入佐证。

（1）黄河源区现代白河坡降变大，河道宽度趋小，曲率越小，点坝砂体规模趋小；坡降变小，河道宽度趋大，曲率越大，点坝砂体规模相对较大。

（2）黄河源区白河流域点坝长度、点坝宽度与河道宽度两两均成正相关关系，点坝宽度与河道宽度的相关性最强，点坝长度比河道宽度对点坝宽度的影响小。按曲率划分后，点坝长度与河道宽度、点坝宽度与点坝长度间的相关系数高于所有数据参数分析结果，且不同曲率条件下相关性差异较大，点坝的发育受河流弯曲程度的影响。