2. 中国石油大学(北京)非常规油气科学技术研究院,北京 102249;
3. 中国石油西南油气田公司 页岩气研究院,成都 610051;
4. 中国石油大学(北京)理学院,北京 102249
2. Research Institute of Unconventional Oil and Gas Science and Technology, China University of Petroleum(Beijing), Beijing 102249, China;
3. Shale Gas Research Institute, PetroChina Southwest Oil & Gas Field Company, Chengdu 610051, China;
4. College of Science, China University of Petroleum(Beijing), Beijing 102249, China
近年来,随着非常规油气领域探索的不断深入,页岩油气勘探开发已然成为全球油气资源勘探的热点方向。有机质碳含量(TOC)作为评价烃源岩生烃潜力及预测储层油气“甜点区”的关键性指标,对于页岩气勘探开发以及资源评价具有指导意义,但其值准确性受到地质条件复杂程度及测定方法差异等一系列因素的影响。目前,尽管地球化学方法被认为是测量TOC含量最受欢迎的方法,但有些缺陷可能会影响结果的可靠性,例如,不能覆盖大范围的深度,成本高且耗时。此外,由于样品长时间暴露在空气中,测量往往不准确,这增加了游离有机物被氧化和逸出的机会。利用测井资料预测TOC含量也是常用手段,其常规方法有多元回归法和ΔlogR法,但这2种方法都存在一定缺陷[1-3]。多元回归法将TOC含量与一系列测井参数之间建立多元回归关系,但因TOC含量往往受多种地质因素的影响,且与各因素间存在着复杂的非线性关系,常规的回归方法难以表达其内在联系,预测效果难以达到要求[4-7]。ΔlogR法通过将对数坐标的电阻率曲线与算术坐标的声波时差曲线叠加,以非烃源岩段调准基线计算幅度差ΔlogR[8-9],该方法需要设定有机碳背景值(泥岩普遍含有一定量的有机碳)、成熟度参数及人为对准多个非烃源岩基线,操作复杂、误差较大,对于异常点处理并没有系统的标准,人为主观性较强[10-11]。如今随着人工智能领域与各个学科相互交叉融合,机器学习方法在地质领域得到了一系列的应用,通过引用不同的人工智能算法实现对烃源岩TOC含量的准确预测[12-14]。常用的机器学习方法主要包括神经网络、支持向量机、极限学习等[15-17]。为了进一步提高预测精度,国内外学者通过结合具体研究区特点,不断优化算法,降低预测误差[18]。王贵文等[19]使用BP神经网络模型对塔里木盆地台盆区寒武系—奥陶系烃源岩进行了TOC含量预测,取得了较好的效果;蒋德鑫等[20]对珠江口盆地陆丰凹陷文昌组烃源岩与TOC含量建立多元回归模型、人工神经网络模型和曲线叠合模型,并分析了3种模型的预测效果及适用条件。Johnson等[21]使用改进的神经网络模型对澳大利亚坎宁盆地烃源岩TOC含量进行了预测并达到了基本精度要求。上述方法虽取得了一定效果,但预测精度还有待提高,且在不同地区适用性不同,针对四川盆地尚未提出有效预测方法。
以川南五峰组—龙马溪组为例,首先采集该地区多口井的测井曲线及实测TOC含量数据进行建模,然后利用主成分分析法对收集的测井资料进行预处理,建立并训练基于BP神经网络模型和基于梯度提升决策树(Gradient Boosting Decision Tree,GBDT)的预测模型,并将这2种模型应用于生产井的TOC含量预测中验证其准确性,以期为该区TOC含量预测提供新思路,为后续勘探开发提供依据。
1 地质概况四川盆地位于上扬子台地西北部,在龙门山—大巴山台缘坳陷和滇黔川鄂台褶带中间,是经历多期复杂构造运动后形成的叠合深层盆地。在奥陶纪晚期,受到南部黔中隆起、西部川中隆起以及东部雪峰古隆起的相互作用,四川盆地逐渐由早中奥陶世广阔海域逐渐转变为被东南西三面隆起包围的半局限性海域,沉积主体也演变为半局限浅海相和深水—半深水陆棚亚相[22-23]。
根据川南长宁、泸州等地区页岩气勘探开发资料显示,该地区下古生界海相黑色富有机质页岩广泛发育,4 500 m以浅的五峰龙马溪组成为黑色泥页岩具有分布范围广、有机质(TOC)含量高、成熟度高等一系列优点,已经成为了我国南方海相页岩气主力开发层系,2020年产量已达200亿m3,该层位页岩气资源量达到3.7万亿m3,可采资源量达200亿m3,具有极高的勘探开发价值。本次研究所涉及的区域主要为长宁和泸州地区,所涉及的地层主要为五峰组—龙马溪组页岩层系。
2 TOC含量预测模型本次研究中井径和地层电阻率等一系列测井数据、实测TOC含量数据均来源于中国石油西南油气田公司页岩气研究院,测试仪器为碳硫分析仪KLT-005,测试温度为16~18 ℃。为改进常规地球化学方法测定TOC含量时样品长时间暴露在空气中导致测量不准确的弊端,本次样品密闭取心,封闭保存,并通过调研前人对于研究区TOC含量的测定结果,与实测值进行比对,确保了测试的准确性。为了减弱个别参数不准确对模型精度的影响,采用主成分分析法对收集到的各项测井数据进行优选,得到新的输入变量,并分别代入BP和GBDT预测模型中进行训练,调整各项参数使模型均方根误差达到最小,利用建立的预测模型对不同页岩气井进行TOC含量的预测。
2.1 主成分分析主成分分析法的主要原理是利用降维的方法,以丢失较少的信息为前提,把多个相互关联的参数转化为几个综合性参数的一种多元统计方法。利用此方法转化、生成的综合性参数称为主成分,其中每个主成分都是原始变量的线性组合,且各个主成分之间互不相关,利用此方法得到的主成分相比初始变量数据具有更为简洁准确的性能[24-27]。
进行主成分分析,首先需要将原始数据进行标准化处理,以此来消除量纲所带来的影响。假设进行主成分分析的指标有m个:x1,x2,x3,…,xm,评价对象共有n个,其中第1个评价对象的第j个指标的取值为x1j,通过此方法可将原始数据排列为矩阵
将各个指标值xij转换为标准指标
| $ \tilde{x}_{i j}=\frac{x_{i j}-\bar{x}_{j}}{s_{j}}, (i=1, 2, \cdots, n ; i=1, 2, \cdots, m) $ | (1) |
其中
| $ \bar{x}_{j}=\frac{1}{n} \sum\limits_{i=1}^{n} x_{i j} $ | (2) |
| $ s_{j}=\frac{1}{n-1} \sum\limits_{i=1}^{n}\left(x_{i j}-\bar{x}_{j}\right)^{2}, \quad(j=1, 2, \cdots, m) $ | (3) |
| $ \tilde{x}_{i}=\frac{x_{i}-\bar{x}_{i}}{s_{i}}, \quad(i=1, 2, \cdots, m) $ | (4) |
式中:xj,sj,
其次建立变量之间的相关系数矩阵R,其中
| $ \boldsymbol{R}=\left(r_{i j}\right)_{m \times m} $ | (5) |
| $ r_{i j}=\frac{\sum\limits_{k=1}^{n} \tilde{x}_{k i} \times \tilde{x}_{k j}}{n-1}, \quad(i, j=1, 2, \cdots, m) $ | (6) |
式中:rij = 1,rij = rji,rij是第i个指标与第j个指标的相关系数。
计算相关系数矩阵R的特征值λ1 ≥ λ2… ≥ λm ≥ 0,及对应的特征向量u1,u2,um,其中
| $ u_{j}=\left(u_{1 j}, u_{2 j}, \cdots, u_{n j}\right)^{T} $ | (7) |
由特征向量组成m个新的指标变量。式中y1是第1主成分,y2是第2主成分,…ym是第m主成分。
| $ y_{1} =u_{11} \tilde{x}_{1}+u_{21} \tilde{x}_{2}+\cdots+u_{n 1} \tilde{x}_{n} $ | (8) |
| $ y_{2} =u_{12} \tilde{x}_{1}+u_{22} \tilde{x}_{2}+\cdots+u_{n 2} \tilde{x}_{n} $ | (9) |
| $ y_{m} =u_{1 m} \tilde{x}_{1}+u_{2 m} \tilde{x}_{2}+\cdots+u_{n m} \tilde{x}_{n} $ | (10) |
最后确定主成分个数:
| $ \alpha_{k}= \frac{\lambda_{k}}{\sum\limits_{k=1}^{m} \lambda_{k}} $ | (11) |
| $ \alpha_{P}= \frac{\sum\limits_{k=1}^{p} \lambda_{k}}{\sum\limits_{k=1}^{m} \lambda_{k}} $ | (12) |
式中:αk为各个主成分的贡献率;αP为主成分y1,y2,…,yp的累计贡献率。
当累计贡献率αP大于或等于80%~85% 时,选择其相对应的前p个指标变量作为主成分分析得到的主成分,用这p个主成分替代m个初始变量指标,更加简便准确。
收集川南长宁、泸州等地区多口井的测井曲线及龙马溪组17口井627组实测TOC含量数据,分别将一系列不同测井参数和其对应的TOC含量进行相关性分析,优选出相关性较高的7个测井参数:声波时差(AC)、井径(CAL)、补偿中子(CNL)、补偿密度(DEN)、自然伽马(GR)、无铀伽马(KTH)和地层深电阻率(RLLD),作为评价分析TOC含量的影响因子[28]。
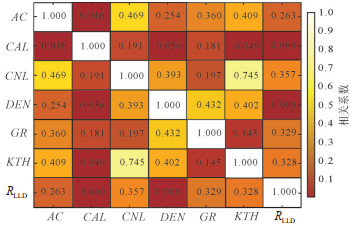
在创建预测模型时,仅使用任何单一测井参数均无法准确预测TOC含量,为了达到准确得到TOC含量与各个测井曲线间的非线性映射关系的目的,对以上7组测井参数进行主成分分析,计算相关系数矩阵,其中相关性系数越靠近1,则表明测井参数间的相关性越好,反之则相关性越差,结果如图 1所示。
|
下载原图 图 1 输入特征变量关联度分析表 Fig. 1 Correlation analysis of input characteristic variables |
分析计算得到各成分对于7个测井参数信息的贡献率和累计贡献率(表 1)。
|
|
下载CSV 表 1 主成分特征值及贡献率 Table 1 Eigenvalues and contribution rate of the principal components |
将贡献率从高至低排列,前4个主成分的累计贡献率达到了86.505%,依据累计贡献率大于85% 的原则,选取前4个主成分作为新的输入变量,应用于建立TOC含量计算模型中。表 2为主成分的因子载荷矩阵,反映各指标对主成分载荷的相对大小和作用方向。
|
|
下载CSV 表 2 主成分的因子载荷矩阵 Table 2 Factor loading matrix of the principal components |
利用表 2和4个主成分初始特征值,计算得到新的输入变量y1,y2,y3,y4公式:
| $ \begin{aligned} y_{1}=& 0.879 x_{1}+0.828 x_{2}+0.668 x_{3}+0.200 x_{4}+\\ & 0.441 x_{5}-0.159 x_{6}-0.600 x_{7} \end{aligned} $ | (13) |
| $ \begin{aligned} y_{2}=& 0.267 x_{1}+0.352 x_{2}-0.367 x_{3}+0.902 x_{4}-\\ & 0.710 x_{5}+0.221 x_{6}+0.188 x_{7} \end{aligned} $ | (14) |
| $ \begin{aligned} y_{3}=&-0.137 x_{1}+0.132 x_{2}+0.283 x_{3}-0.151 x_{4}-\\ & 0.039 x_{5}+0.941 x_{6}-0.032 x_{7} \end{aligned} $ | (15) |
| $ \begin{aligned} y_{4}=& 0.141 x_{1}+0.086 x_{2}+0.431 x_{3}-0.105 x_{4}-\\ & 0.105 x_{5}-0.118 x_{6}+0.724 x_{7} \end{aligned} $ | (16) |
经过主成分分析得到了新的4个综合变量y1,y2,y3,y4,各个综合变量之间相互独立,每个综合变量都包含前述7个测井参数信息,但各有侧重。根据各个系数大小可以看出,y1主要反映了AC和CAL的信息;y2主要反映了DEN和GR的信息;y3主要反映了KTH的信息;y4主要反映了CNL和RLLD的信息。
2.2 BP神经网络模型BP神经网络是一种按照反向误差进行传播的多层前馈网络,利用学习信号正向传播和误差逆向传播双重作用机制来对数据进行训练。BP算法是以网络误差平方为目标函数、采用梯度下降法来计算目标函数的最小值[29-30]。通过正向传播,隐含层可通过内部计算获取输入向量的输出值,输出层则会在隐含层的基础上进行计算,进而得到输出值。当进行反向传播时,首先需要计算出输出层所得到的输出值,若获得的输出值达不到预期效果,则会重新将数据导入输入层,再通过不断修改输入层与隐含层,隐含层与输出层的连接强度和阈值,直到使误差控制住预期范围内,训练则会停止[31]。经过此方法训练好的神经网络则具有很强的非线性映射能力和柔性的网络结构。
本文建立的BP神经网络主要包含输入层、隐含层和输出层三部分结构。模型借助Matlab软件编写模型程序,并使用工具箱中newff函数创建神经网络,再利用经过主成分分析法降维后得到的4个新的综合性参数y1,y2,y3,y4作为模型的输入变量,将实测得到的TOC含量作为模型的输出变量,隐含层的传递函数选择tansig函数,输出层传递函数则选择pureline线性函数,隐函数节点数计算公式如下:
| $ \sum\limits_{i=0}^{n} C_{M}^{i}>k $ | (17) |
式中:k为样本数,个;M为隐含层神经元的数量,个;n为输入层神经元的个数;i为取值0~n的正整数,当i > M,CMi = 0。
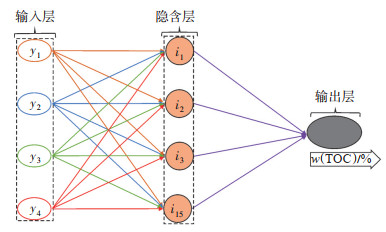
样本数为627,选取隐含层神经元个数M = 15,最终确立的网络结构为4×15×1的3层BP神经网络模型,为使算法达到较快的收敛速度和较高的训练精度,网络训练采用rainlm函数,神经网络模型具体相关参数如表 3所列。利用学习后的神经网络模型对测试集进行识别,通过计算误差率,分析训练模型准确率,具体拓扑图如图 2所示。
|
|
下载CSV 表 3 BP神经网络模型相关参数 Table 3 Relevant parameters of BP neural network model |
|
下载原图 图 2 BP神经网络模型拓扑图 Fig. 2 Topological diagram of BP neural network model |
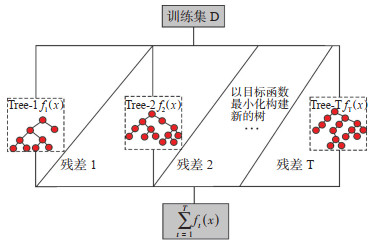
GBDT是一种具有出色预测能力的机器学习模型。通过回归树将计算值与目标值之间的残差进行快速归类分析,并利用逐步提升算法不断减小残差,使得计算值逐渐逼近目标值[32-34]。这种方法不仅能灵活处理各种类型的数据,还能在极短的调参时间下,达到较高的预测精度。由于回归树会对不同的残差值进行不同处理,即使样本中有错误样点,训练结果也不会受到太大影响。此外,模型还可通过调整参数和使用更多回归树来挖掘出数据之间的对应关系,使其具备较好的泛化能力。GBDT算法的核心是在多次基础模型中,利用损失函数的负梯度值作为该轮基础模型损失值的近似值,并通过这一近似值来构建下一轮的基础模型,能使目标函数的求解更为简便。GBDT算法的实现步骤如图 3所示。
|
下载原图 图 3 GBDT模型的实现框图 Fig. 3 Implementation block diagram of GBDT model |
此模型利用Python语言编写模型程序,并借助机器学习库内Sklearn模块来进行建模分析。模型主要调节参数为Boosting框架参数和弱学习器参数[35]。其中Boosting框架的重要参数主要包括:最大迭代次数、权重缩减系数、损失函数等;弱学习器的主要参数包括:最大特征数、决策树最大深度、叶子节点最少样本数等。为了使得预测模型取得较好的效果,在建立模型前,需对模型参数进行调整。选择参数时,迭代次数过小,容易出现欠拟合的情况;学习速率过小,则需要更为复杂的迭代过程和更大的计算量;过大的叶子节点深度会出现模型过拟合现象。因此,采用交叉验证的方法来确定合理的参数体系,参数选取原则主要是利用准确率判断模型拟合的好坏,通过不断调整合适的参数以达到较高的准确率,模型具体参数如表 4所列。
|
|
下载CSV 表 4 GBDT模型相关参数 Table 4 Relevant parameters of GBDT model |
具体建模操作流程如下:
(1)输入。
训练数据集:
| $ \boldsymbol{D}=\left[\left(y_{11}, \cdots, y_{14}, Y_{1}\right), \left(y_{627, 1}, \cdots, y_{627, 4}, Y_{627}\right)\right] $ | (18) |
损失函数:
| $ L[Y, f(y)]=\frac{1}{2}[Y-f(y)]^{2} $ | (19) |
式中:Y为实测TOC质量分数,%。
(2)初始化弱分类器。
对损失函数进行求导,令其导数为零,得到使损失函数达到极小值的常数c。因此初始化时,c值可取训练样本标签值的均值,即
| $ f(y)=c=\frac{\sum\limits_{i=0}^{627} Y_{i}}{627} $ | (20) |
计算损失函数的负梯度值,即:
| $ r_{m i}=-\left\{\frac{\partial L\left[Y_{i}, f\left(y_{i}\right)\right]}{\partial f\left(y_{i}\right)}\right\}_{f(y)=f_{m-1}(y)}=Y_{i}-f\left(y_{i}\right) $ | (21) |
式中:i为样本数,个,i = 1,2,…,627;m为迭代次数,即生成的基础模型的个数,m = 1,2,…,M。
利用上式得到的数据集(yi,rmi)来拟合下一轮的基础模型,训练得到模型的回归树ft(y),计算每个叶子节点Rmj,j表示叶子节点数,j = 1,2,…,J,并计算每个叶子节点Rmj的最佳拟合值rmj,使得其损失函数达到最小。
| $ r_{m j}=\frac{1}{M} \sum y_{i} \in R_{m j}\left[Y_{i}-f\left(y_{i}\right)\right] $ | (22) |
则
| $ f_{m}(y)=f_{m-1}(y)+\sum\limits_{j=1}^{J} r_{m j} I\left(y \in R_{m j}\right) $ | (23) |
结合前m - 1轮基础模型,可得到最终模型:
| $ \begin{aligned} f_{M}(y)=&\frac{\sum\limits_{i=0}^{627} Y_{i}}{627}+\sum\limits_{m=1}^{M} \sum\limits_{j=1}^{j} \frac{1}{M} \sum y_{i} \in R_{m j}\left[Y_{i}-f\left(y_{i}\right)\right] . \\ &I\left(y \in R_{m j}\right) \end{aligned} $ | (24) |
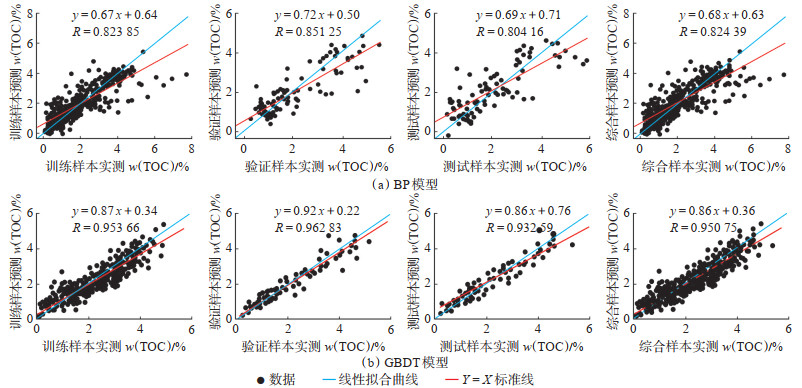
对川南五峰组—龙马溪组17口井627组实测数据分别按照训练样本70%、验证样本15%、测试样本15% 的比例进行划分,即439组数据作为训练样本,94组数据作为验证验本、94组数据作为测试样本。BP神经网络模型与GBDT模型对于TOC含量的预测结果如图 4所示,2种模型对于TOC含量的预测效果均较好,GBDT模型的综合效果要好于BP神经网络,其预测值整体偏离TOC含量实测值程度较小,相关性更高,达0.90以上。
|
下载原图 图 4 2种模型训练及预测结果 Fig. 4 Training and prediction results of two models |
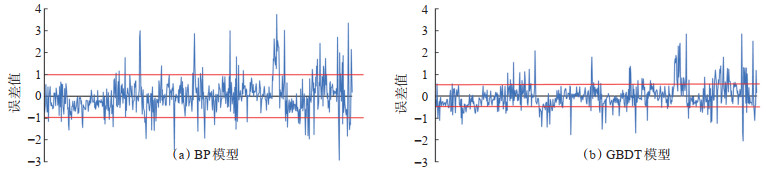
分别计算两者对于627组数据预测与真实TOC含量之间的误差(图 5),GBDT模型整体误差更小,绝大部分误差值均在0.5范围内,由此认为GBDT模型在预测TOC含量方面更具优越性。
|
下载原图 图 5 2种模型预测误差结果 Fig. 5 Prediction errors of two models |
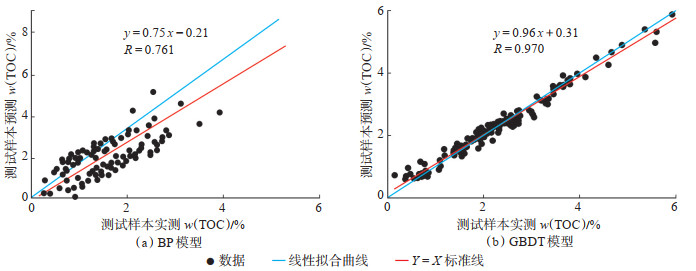
根据上述的2种TOC含量预测模型,利用川南长宁CNX202井五峰组—龙马溪组131组测井数据对页岩气TOC含量进行预测。将经过主成分分析的数据输入训练好的模型中,如图 6所示,BP模型测试样本的预测值与实测值相关性为0.761,GBDT模型测试样本的预测值与实测值相关性为0.970。
|
下载原图 图 6 2种模型预测预测结果 Fig. 6 Prediction results of two models |
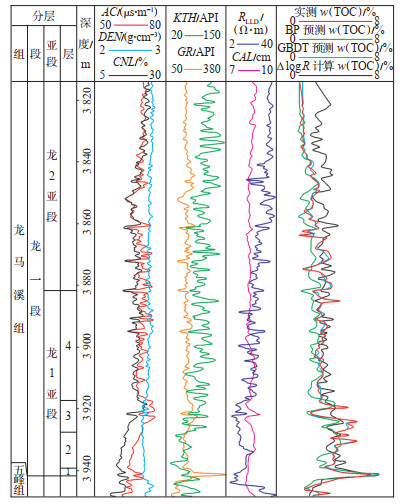
以长宁CNX202井为例,综合对比上述2种预测模型与传统ΔlogR法对于TOC含量的预测效果(图 7)可知,2种预测模型的预测精度均高于传统ΔlogR方法。
|
下载原图 图 7 川南长宁地区CNX202井五峰组—龙马溪组TOC含量综合对比图 Fig. 7 Comparison between predicted and measured TOC content of Wufeng-Longmaxi Formation of well CNX202 in Changning area, southern Sichuan Basin |
为了更加准确地评价3种预测方法的优劣,采用平均误差、平均误差率、均方根误差等3种误差指标进行对比(表 5)。根据对比结果显示,BP神经网络和GBDT预测模型各误差指标参数均小于传统ΔlogR法,GBDT预测模型表现出更高的准确度。
|
|
下载CSV 表 5 3种模型误差指标对比 Table 5 Comparison of error indexes of three models |
(1)优选出相关性较高的声波时差(AC)、井径(CAL)、补偿中子(CNL)、补偿密度(DEN)、自然伽马(GR)、无铀伽马(KTH)和地层深电阻率(RLLD)等7个测井参数作为评价TOC含量的重要影响因子,利用主成分分析方法,将这7个测井参数转化为4个综合指标,增加了计算精度和计算效率,减少计算冗余。
(2)在川南长宁地区五峰组—龙马溪组采用BP神经网络模型和GBDT模型预测TOC含量,训练样本与测试样本的预测值与实测值相关性均超过0.80,拟合效果均良好,GBDT模型预测精度更高,其预测值与真实TOC含量值的相关性达0.90以上,预测误差更小,627组样本数据中绝大多数的误差值在0.5以内,表现出更稳定的优势。
(3)BP神经网络模型和GBDT模型均能较好的预测川南长宁地区五峰组—龙马溪组TOC含量,预测效果均好于常规ΔlogR方法,其中GBDT模型预测结果与实际测试值偏差更小,该方法在泸州、长宁等地区有广阔的应用前景。
| [1] |
PASSEY Q R, CREANEY S, KULLA J B, et al. A practical model for organic richness from porosity and resistivity logs. AAPG Bulletin, 1990, 74(12): 1777-1794. |
| [2] |
赵万金, 高海燕, 闫国亮, 等. 基于最优化估算和贝叶斯统计的TOC预测技术. 岩性油气藏, 2020, 32(1): 86-93. ZHAO W J, GAO H Y, YAN G L, et al. TOC prediction technology based on optimal estimation and Bayesian statistics. Lithologic Reservoirs, 2020, 32(1): 86-93. |
| [3] |
严伟, 刘帅, 冯明刚, 等. 四川盆地丁山区块页岩气储层关键参数测井评价方法. 岩性油气藏, 2019, 31(3): 95-104. YAN W, LIU S, FENG M G, et al. Well logging evaluation methods of key parameters for shale gas reservoir in Dingshan block, Sichuan Basin. Lithologic Reservoirs, 2019, 31(3): 95-104. |
| [4] |
杜江民, 张小莉, 钟高润, 等. 致密油烃源岩有机碳含量测井评价方法优选及应用: 以鄂尔多斯盆地延长组长7段烃源岩为例. 地球物理学进展, 2016, 31(6): 2526-2533. DU J M, ZHANG X L, ZHONG G R, et al. Analysis on the optimization and application of well logs identification methods for organic carbon content in source rocks of the tight oil: Illustrated by the example of the source rocks of Chang 7 member of Yanchang Formation in Ordos Basin. Progress in Geophysics, 2016, 31(6): 2526-2533. |
| [5] |
SCHMOKER J W. Determination of organic-matter content of Appalachian Devonian Shales from gamma-ray logs. AAPG Bulletin, 1981, 65(7): 1285-1298. |
| [6] |
HESTER T C, SCHMOKER J W. Determination of organic content from formation-density logs, Devonian-Mississippian Woodford Shale, Anadarko Basin, Oklahoma. US Geological Survey, 1987. |
| [7] |
陈浩, 刘洛夫, 窦文超, 等. 银额盆地居延海坳陷烃源岩TOC测井预测方法优选及应用. 地球物理学进展, 2019, 34(3): 1017-1024. CHEN H, LIU L F, DOU W C, et al. Optimal selection and application of prediction methods for TOC of source rocks based on logging data in Juyanhai Depression, Yingen-Ejin Banner Basin. Progress in Geophysics, 2019, 34(3): 1017-1024. |
| [8] |
朱振宇, 刘洪, 李幼铭. ΔlogR技术在烃源岩识别中的应用与分析. 地球物理学进展, 2003, 18(4): 647-649. ZHU Z Y, LIU H, LI Y M. The analysis and application of ΔlogR method in the source rock's identification. Progress in Geophysics, 2003, 18(4): 647-649. DOI:10.3969/j.issn.1004-2903.2003.04.012 |
| [9] |
王祥, 马劲风, 张新涛, 等. 一种考虑密度因素的广义ΔlogR法预测总有机碳含量: 以渤中凹陷西南部陆相深层烃源岩为例. 地球物理学进展, 2020, 35(4): 1471-1480. WANG X, MA J F, ZHANG X T, et al. A generalized ΔlogR method for predicting total organic carbon content considering density factor: A case study of deep continental source rocks in southwest Bozhong Sag. Progress in Geophysics, 2020, 35(4): 1471-1480. |
| [10] |
郭泽清, 孙平, 刘卫红. 利用ΔlogR技术计算柴达木盆地三湖地区第四系有机碳. 地球物理学进展, 2012, 27(2): 626-633. GUO Z Q, SUN P, LIU W H. Calculation of quaternary organic carbon in Sanhu area of Qaidam Basin using ΔlogR technology. Progress in Geophysics, 2012, 27(2): 626-633. DOI:10.6038/j.issn.1004-2903.2012.02.027 |
| [11] |
刘超, 印长海, 卢双舫. 变系数ΔlogR烃源岩测井评价技术关键参数厘定方法及应用. 天然气地球科学, 2015, 26(10): 1925-1931. LIU C, YIN C H, LU S F. Predicting key parameters for variablecoefficient ΔlogR logging technique and its application in source rocks evaluation. Natural Gas Geoscience, 2015, 26(10): 1925-1931. DOI:10.11764/j.issn.1672-1926.2015.10.1925 |
| [12] |
叶绍泽, 曹俊兴, 吴施楷, 等. 基于深度置信网络的总有机碳含量预测方法. 地球物理学进展, 2018, 33(6): 304-311. YE S Z, CAO J X, WU S K, et al. Prediction method of total organic carbon content based on deep belief nets. Progress in Geophysics, 2018, 33(6): 304-311. |
| [13] |
杨洋, 石万忠, 张晓明, 等. 页岩岩相的测井曲线识别方法: 以焦石坝地区五峰组—龙马溪组为例. 岩性油气藏, 2021, 33(2): 135-146. YANG Y, SHI W Z, ZHANG X M, et al. Identification method of shale lithofacies by logging curves: A case study from WufengLongmaxi Formation in Jiaoshiba area, SW China. Lithologic Reservoirs, 2021, 33(2): 135-146. |
| [14] |
刘跃杰, 刘书强, 马强, 等. BP神经网络法在三塘湖盆地芦草沟组页岩岩相识别中的应用. 岩性油气藏, 2019, 31(4): 101-111. LIU Y J, LIU S Q, MA Q, et al. Application of BP neutral network method to identification of shale lithofacies of Lucaogou Formation in Santanghu Basin. Lithologic Reservoirs, 2019, 31(4): 101-111. |
| [15] |
朱振宇, 王贵文, 朱广宇. 人工神经网络法在烃源岩测井评价中的应用. 地球物理学进展, 2002, 17(1): 137-140. ZHU Z Y, WANG G W, ZHU G Y. The application of artificial neural network to the source rock's evaluation. Progress in Geophysics, 2002, 17(1): 137-140. DOI:10.3969/j.issn.1004-2903.2002.01.019 |
| [16] |
DE S, VIKRAM V K, SENGUPTA D. Application of support vector regression analysis to estimate total organic carbon content of Cambay shale in Cambay Basin, India: A case study. Petroleum Science and Technology, 2019, 37(10): 1155-1164. DOI:10.1080/10916466.2019.1578798 |
| [17] |
SHI X, WANG J, LIU G, et al. Application of extreme learning machine and neural networks in total organic carbon content prediction in organic shale with wire line logs. Journal of Natural Gas Science and Engineering, 2016, 33: 687-702. DOI:10.1016/j.jngse.2016.05.060 |
| [18] |
RUI J, ZHANG H, REN Q, et al. TOC content prediction based on a combined Gaussian process regression model. Marine and Petroleum Geology, 2020, 118: 104429. DOI:10.1016/j.marpetgeo.2020.104429 |
| [19] |
王贵文, 朱振宇, 朱广宇. 烃源岩测井识别与评价方法研究. 石油勘探与开发, 2002, 29(4): 50-52. WANG G W, ZHU Z Y, ZHU G Y. Logging identification and evaluation of Cambrian-Ordovician source rocks in syneclise of Tarim Basin. Petroleum Exploration and Development, 2002, 29(4): 50-52. DOI:10.3321/j.issn:1000-0747.2002.04.015 |
| [20] |
蒋德鑫, 姜正龙, 张贺, 等. 烃源岩总有机碳含量测井预测模型探讨: 以陆丰凹陷文昌组为例. 岩性油气藏, 2019, 31(6): 112-120. JIANG D X, JIANG Z L, ZHANG H, et al. Well logging prediction models of TOC content in source rocks: A case of Wenchang Formation in Lufeng Sag. Lithologic Reservoirs, 2019, 31(6): 112-120. |
| [21] |
JOHNSON L M, REZAEE R, KADKHODAIE A, et al. Geochemical property modelling of a potential shale reservoir in the Canning Basin(western Australia), using artificial neural networks and geostatistical tools. Computers & Geosciences, 2018, 120: 73-81. |
| [22] |
高乔, 王兴志, 朱逸青, 等. 川南地区龙马溪组元素地球化学特征及有机质富集主控因素. 岩性油气藏, 2019, 31(4): 72-84. GAO Q, WANG X Z, ZHU Y Q, et al. Elemental geochemical characteristics and main controlling factors of organic matter enrichment of Longmaxi Formation in southern Sichuan. Lithologic Reservoirs, 2019, 31(4): 72-84. |
| [23] |
刘文平, 周政, 吴娟, 等. 川南盆地长宁页岩气田五峰组—龙马溪组成藏动力学过程及其意义. 南京大学学报(自然科学), 2020, 56(3): 393-404. LIU W P, ZHOU Z, WU J, et al. Hydrocarbon generation and shale gas accumulation in the Wufeng-Longmaxi formations, Changning shale-gas field, southern Sichuan Basin. Journal of Nanjing University(Natural Science), 2020, 56(3): 393-404. |
| [24] |
黄利文. 基于理想点的主成分分析法在综合评价中的应用. 统计与决策, 2021, 37(10): 184-188. HUANG L W. Application of principal component analysis based on ideal point in comprehensive evaluation. Statistics and Decision, 2021, 37(10): 184-188. |
| [25] |
黄继盛, 姚康, 束洪春, 等. 基于主成分分析和SVM模型的配电网故障选线方法. 昆明理工大学学报(自然科学版), 2021, 46(4): 1-12. HUANG J S, YAO K, SHU H C, et al. Method of fault line selection in distribution network based on principal component analysis and SVM model. Journal of Kunming University of Science and Technology(Natural Science Edition), 2021, 46(4): 1-12. |
| [26] |
张继伟. 基于主成分分析的页岩油有利区评价: 以仪陇—平昌地区大安寨段为例. 断块油气田, 2021, 28(1): 28-32. ZHANG J W. Evaluation of favorable areas of shale oil based on principal component analysis: Taking Daanzhai member of Yilong-Pingchang area as an example. Fault Block Oil and Gas Field, 2021, 28(1): 28-32. |
| [27] |
周游, 张广智, 高刚, 等. 核主成分分析法在测井浊积岩岩性识别中的应用. 石油地球物理勘探, 2019, 54(3): 667-675. ZHOU Y, ZHANG G Z, GAO G, et al. Application of kernel principal component analysis in well logging turbidite lithology identification. Oil Geophysical Prospecting, 2019, 54(3): 667-675. |
| [28] |
曲彦胜, 钟宁宁, 刘岩, 等. 烃源岩有机质丰度的测井计算方法及影响因素探讨. 岩性油气藏, 2011, 23(2): 80-84. QU Y S, ZHONG N N, LIU Y, et al. Using logging methods to calculate organic matter abundance of source rocks and its influencing factors. Lithologic Reservoirs, 2011, 23(2): 80-84. DOI:10.3969/j.issn.1673-8926.2011.02.015 |
| [29] |
周瑾, 白洪溪, 崔健, 等. 基于电磁参数的BP神经网络模型在页岩气储层预测中的应用研究. 物探化探计算技术, 2020, 42(1): 76-83. ZHOU J, BAI H X, CUI J, et al. Application of BP neural network model based on electromagnetic parameters in shale gas reservoir prediction. Geophysical and Geochemical Calculation Technology, 2020, 42(1): 76-83. |
| [30] |
袁颖, 谭丁, 于少将, 等. 基于贝叶斯正则化改进BP神经网络的页岩气有机碳含量预测模型. 地质与勘探, 2019, 55(4): 1082-1091. YUAN Y, TAN D, YU S J, et al. A Prediction model for shale gas organic carbon content based on improved BP neural network using Bayesian regularization. Geology and Exploration, 2019, 55(4): 1082-1091. |
| [31] |
朱红, 孔德群, 钱旭. 基于ATD-BP神经网络的页岩气产量预测方法. 科学技术与工程, 2017, 17(31): 128-132. ZHU H, KONG D Q, QIAN X. Shale gas production prediction method based on adaptive threshold denoising BP Neural Network. Science Technology and Engineering, 2017, 17(31): 128-132. DOI:10.3969/j.issn.1671-1815.2017.31.020 |
| [32] |
谷宇峰, 张道勇, 鲍志东. PSO-GBDT识别致密砂岩储集层岩性研究: 以姬塬油田西部长4+5段为例. 矿物岩石地球化学通报, 2021, 40(3): 624-634. GU Y F, ZHANG D Y, BAO Z D. Lithology prediction of tight sandstone reservoirs using the PSO-GBDT: A case study of the Chang 4 + 5 members in the western Jiyuan Oilfield. Mineral and Petrochemical Bulletin, 2021, 40(3): 624-634. |
| [33] |
谷宇峰, 张道勇, 鲍志东, 等. 利用梯度提升决策树(GBDT) 预测渗透率: 以姬塬油田西部长4+5段致密砂岩储层为例. 地球物理学进展, 2021, 36(2): 585-594. GU Y F, ZHANG D Y, BAO Z D, et al. Permeability prediction using Gradient Boosting Decision Tree(GBDT): A case study of tight sandstone reservoirs of member of Chang 4+5 in western Jiyuan Oilfield. Progress in Geophysics, 2021, 36(2): 585-594. |
| [34] |
谷宇峰, 张道勇, 鲍志东, 等. 利用GBDT识别致密砂岩储层岩性. 地球物理学进展, 2021, 36(5): 1956-1965. GU Y F, ZHANG D Y, BAO Z D, et al. Identification of tight sandstone reservoir lithology using GBDT. Progress in Geophysics, 2021, 36(5): 1956-1965. |
| [35] |
尹超英, 邵春福, 黄兆国, 等. 基于梯度决策树的多尺度建成环境对小汽车拥有的影响. 吉林大学学报(工学版): 1-8[2021-11-02]. https://doi.org/10.13229/j.cnki.jdxbgxb20200844. YIN C Y, SHAO C F, HUANG Z G, et al. Investigating the influences of multi-scale built environment on car ownership behavior based on gradient boosting decision trees. Journal of Jilin University(Engineering Edition): 1-8[2021-11-02]. https://doi.org/10.13229/j.cnki.jdxbgxb20200844. |
 2022, Vol. 34
2022, Vol. 34




