传统的逆时偏移方法(RTM)具有无倾角限制的优点,能够处理纵、横向强变速问题,是目前业界公认的解决高陡复杂构造成像的较好方法[1-2]。然而,逆时偏移在浅层成像中存在较强的低频噪音,难以实现保幅成像。最小二乘偏移在反演框架下进行偏移成像,能很好地克服上述问题的影响[3-5]。最小二乘偏移技术经历了射线、单程波和双程波动理论等发展阶段[6-8]。其中,Kirchhoff积分法最小二乘偏移计算效率高,但是精度较低;基于单程波算子的最小二乘叠前深度偏移虽然解决了多路径、焦散等问题,且方便在频率空间域进行Q值补偿,但在复杂地质构造情况下,其计算精度依然无法满足实际生产需要。当前,基于双程波波动方程的最小二乘逆时偏移[9](LSRTM)已成为地球物理界的研究热点。传统的偏移算法大都是基于声波介质推导的,没有考虑地球介质的黏滞性,存在深部储层成像幅值弱的问题。基于黏声介质的偏移成像方法在计算过程中对道集进行校正处理,实现Q值补偿,可以达到保幅处理和提高成像分辨率的目的[10]。相对于声波最小二乘逆时偏移方法,黏声介质中的最小二乘逆时偏移技术在成像过程中考虑了地层的吸收衰减效应[11-13],在理论上具有更加明显的优势。前人在黏声最小二乘偏移技术方面做了大量的研究工作。Mulder等[14]和Hak等[15]在频率空间域分析了黏声介质中地震波偏移成像的多解性,并应用于线性及非线性反演;王雪君等[16]基于点扩散函数的分解与补偿,实现了黏声介质反演成像;李振春等[17]提出了黏声介质时间域最小平方逆时偏移,在对黏滞性吸收进行校正的同时,还克服了频率域方法不能应用于大规模模型的限制;还有学者通过low-rank近似将算法应用到Q补偿的RTM和LSRTM中,并指出了基于Q补偿的LSRTM方法的成像优势。黏声最小二乘偏移由于计算能力的限制,早期发展较缓慢。近年来,计算机技术飞速发展,特别是高性能CPU和GPU等机器设备的诞生,极大地推动了各种先进地球物理方法技术的实用化进程[18]。Micikevicius[19]研究了基于GPU的有限差分实现问题,给出了快速有限差分实现算法。Zhang等[20]实现了基于CPU/GPU异构平台的全波形反演,并在陆上数据进行了初步应用。黏声最小二乘逆时偏移技术在理论上具有明显优势,并已成功应用于海上数据,但在陆地数据应用的实例较少,在三维陆地资料的应用几乎没有成功案例。
本文基于广义标准线性固体(GSLS)模型,建立黏声介质波动方程,制定基于GPU加速的黏声介质中最小二乘逆时偏移实现流程,对理论模型进行测试,并将该方法应用于胜利油田某陆上探区三维地震资料处理,以期提升深层储层成像精度,为岩性油气藏的勘探开发提供依据。
1 基于黏声介质的最小二乘逆时偏移理论 1.1 黏声最小二乘逆时偏移基本原理最小二乘反演成像是一个线性化反问题,用于估计地下介质的高波数扰动量,目前主要是指速度扰动量。其核心是建立一个线性化的正问题,用数值模拟结果(炮道集)去逼近实测的波场扰动。在L2范数意义下,当逼近误差最小时,高波数扰动解就是所要的解。
基于广义标准线性固体(GSLS)模型的波动方程[21-23]表示为
| $ \begin{aligned} \frac{\partial^{2} p}{\partial t^{2}}=& \frac{\partial}{\partial t}\left[M_{\mathrm{R}}\left(1-\sum\nolimits_{i=1}^{I}\left(1-\frac{\tau_{\varepsilon i}}{\tau_{\sigma i}}\right) \mathrm{e}^{-t/t_{\sigma i}}\right) H(t)\right] * \\ & \nabla \cdot\left(\frac{1}{\rho} \nabla p\right)+f^{\prime} \end{aligned} $ | (1) |
式中:MR为松弛模量;τεi与τσi为松弛时间,ms;H(t) 为单位阶跃函数;I为标准线性体的个数;∇ 为梯度算子;∇∙为散度算子;*为时间上的卷积算子;ρ为密度,kg/m3;f'为震源项。
首先,当只有速度为变化量时的黏声介质波动方程为
| $ \begin{aligned} \frac{1}{v^{2}} \frac{\partial^{2} p}{\partial t^{2}}=& \frac{\partial}{\partial t}\left[\rho\left(1-\sum\nolimits_{i=1}^{I}\left(1-\frac{\tau_{\varepsilon i}}{\tau_{\sigma i}}\right) \mathrm{e}^{-t/t_{\sigma i}}\right) H(t)\right] * \\ & \nabla \cdot\left(\frac{1}{\rho} \nabla p\right)+f \end{aligned} $ | (2) |
式中:
然后,引入上述方程的Born近似线性化,其波动方程为
| $ \begin{gathered} \frac{1}{v_{0}^{2}} \frac{\partial^{2} p_{\mathrm{s}}}{\partial t^{2}}=\frac{\partial}{\partial t}\left[\rho\left(1-\sum\nolimits_{i=1}^{I}\left(1-\frac{\tau_{\varepsilon i}}{\tau_{\sigma i}}\right) \mathrm{e}^{-t/t_{\sigma i}}\right) H(t)\right] * \\ \nabla \cdot\left(\frac{1}{\rho} \nabla p_{\mathrm{s}}\right)-m(x) \frac{\partial^{2} p_{0}}{\partial t^{2}} \end{gathered} $ | (3) |
式中:ps为扰动波场;p0为背景波场;m(x) 为慢度扰动量。
上式对应一个线性化的正问题,可写为
| $ \delta {\mathit{\boldsymbol{d}}^{{\rm{cal}}}} = \mathit{\boldsymbol{L}}\delta \mathit{\boldsymbol{m}} $ | (4) |
式中:dcal为计算得到的地震数据;m是地球物理参数矢量,如速度、密度等;L描述了依赖于m的地震波场正传播过程。
最后,定义最小二乘偏移的目标函数为
| $ E(\mathit{\boldsymbol{m}}) = \frac{1}{2}{\left\| {\delta {\mathit{\boldsymbol{d}}^{{\rm{cal}}}} - \delta {\mathit{\boldsymbol{d}}^{{\rm{obs}}}}} \right\|^2} $ | (5) |
式中:dobs为观测到的地震数据;E(m) 为误差泛函。应用迭代算法求解上式,迭代公式为
| $ \delta \boldsymbol{m}^{k+1}=\delta \boldsymbol{m}^{k}+\mu_{k}(\Delta \delta \boldsymbol{m})^{k+1} $ | (6) |
式中:μ为迭代步长;k为迭代次数。
迭代算法的关键是计算(Δδm)k+1,该项实质上是目标泛函的梯度项。梯度项的计算是正传波场和逆时反传波场的相关。
1.2 基于GPU加速的黏声最小二乘逆时偏移流程GPU(图形处理器)是专为执行复杂的数学和几何计算而设计的处理器。在工程领域,通常采用CPU与GPU等2种计算设备协同运算的模式对算法进行加速:由CPU负责数据输入、输出以及逻辑判断,并将这些数据拷贝到GPU显存,在GPU进行核心算法运算,计算完成后,将计算结果从显存拷贝回CPU内存,最后通过CPU输出。
三维黏声最小二乘逆时偏移计算量巨大,应用传统的CPU设备计算耗时长。分析计算流程可知,其中Born正演和梯度计算这2步计算量大。考虑到GPU具有超强的计算性能,应用GPU计算黏声LSRTM中的Born正演模拟和梯度,其他的数据输入、输出及简单计算由CPU完成。基于GPU加速的黏声LSRTM的实现流程如图 1所示。
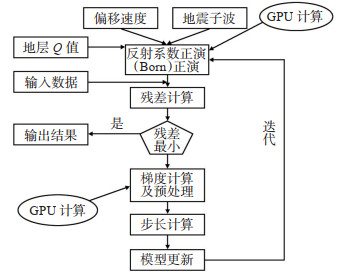
|
下载原图 图 1 基于GPU加速的黏声最小二乘逆时偏移流程 Fig. 1 Process of least-squares reverse time migration in visco-acoustic medium based on GPU acceleration |
理论测试模型采用国际标准的SEG/EAGE盐丘模型。该模型是由来自全球50多个石油公司、科研单位的地球物理学家、地质学家和计算机专家协同合作建立的,目前主要应用于叠前深度偏移成像算法、波动方程正演模拟、速度分析方法、观测系统设计、计算软硬件平台等的模型验证。本文数据的观测参数为:总炮数为4 781;50束线,炮线间距为160 m,炮点间距为80 m;检波线间距为40 m,道间距为40 m;每束线96炮,每炮65道;记录长度为5 s,时间采样间隔为8 ms;空间采样间隔为20 m;表层最小速度为1 500 m/s,盐丘最大速度为4 450 m/s。
地层Q值参数反演的方法有很多,有野外测量法、经验公式法、信号估算法和基于层析理论的估计方法等[24]。李庆忠[25]提出的经验公式所计算的Q值在胜利油田东部探区具有较好的对应关系,并在油田勘探开发中得到了广泛应用。其表达式为
| $ Q_{\mathrm{p}}=14 v_{\mathrm{p}}^{2.2} $ | (7) |
式中:Qp为品质因子;vp为纵波速度,km/s。
为了验证本文方法的有效性,首先进行正演模拟,获取用于偏移算法验证的理论数据。同时输入速度模型[图 2(a)]和用式(7)计算的Q值模型[图 2(b)]进行黏声波动方程正演模拟,生成模拟炮集记录,再分别进行声波最小二乘逆时偏移和黏声最小二乘逆时偏移计算,得到偏移剖面。结果显示,由于考虑了地震波传播过程中的吸收衰减效应,与声波LSRTM[图 2(c)]相比,黏声LSRTM[图 2(d)]偏移剖面地层层位更加清晰、断层刻画更加精细、准确,中、深层能量得到了有效补偿,成像质量明显改进。从这2个偏移剖面中红线处同一位置波形曲线[图 2(e)]可以看出,黏声LSRTM通过在偏移过程中对地震记录进行了Q补偿,其波形[图 2(e)中红线]相对于没有考虑吸收衰减的LSRTM的波形[图 2(e)中绿线],主瓣更窄,分辨率更高,达到了Q补偿提高分辨率的目的。同时,与对声波正演资料进行声波LSRTM偏移的结果[图 2(e)中黑线]相比,波形拟合程度很高,从另一个角度验证了本文方法的有效性和正确性。
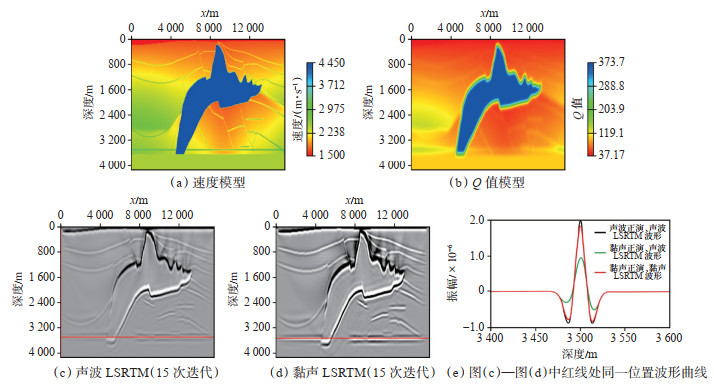
|
下载原图 图 2 理论测试中的速度模型、Q值模型和最小二乘逆时偏移结果 Fig. 2 Velocity model, Q model and least-squares reverse time migration results in theoretical test |
图 3为黏声LSRTM算法迭代的收敛曲线。分析全程30次迭代的收敛曲线可以看出,偏移算法在开始迭代时曲线下降较快,说明收敛速度较快,大约在10次迭代后,曲线变缓,说明迭代残差趋于稳定,达到了较好的收敛结果。
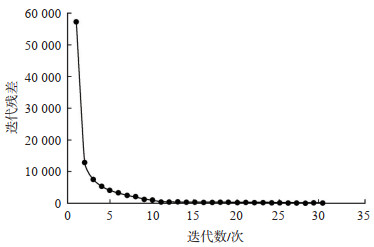
|
下载原图 图 3 黏声最小二乘逆时偏移收敛曲线 Fig. 3 Convergence curve of least-squares reverse time migration in visco-acoustic medium |
本次研究选取了胜利油田某探区三维实际资料进行黏声最小二乘逆时偏移试处理。工区位于东营凹陷东部,处于断裂带和中央隆起带,地下构造复杂,断裂发育,油气资源丰富,油气勘探潜力巨大,油藏类型以构造-岩性油藏为主。
在进行偏移前,首先对炮集数据进行了常规叠前预处理,包括静校正、能量均衡、去噪、直达波切除、面波剔除等,以保证处理后的炮集数据与模型正演的数据能够较好匹配。同时,为了获得准确的速度模型,需要在时间域进行常规的偏移速度分析以获得初始速度模型,然后应用DIX公式将时间域速度转换成深度域速度,最后通过射线层析反演,计算出精确的深度域速度模型。
该区的地层Q值是应用胜利经验公式估算的。胜利浅层Q值计算经验公式为
| $ Q_{\mathrm{p}}=4.93 v_{\mathrm{p}}^{4.45} $ | (8) |
中深层Q值计算经验公式为
| $ Q_{\mathrm{p}}=23.96 v_{\mathrm{p}}^{1.78} $ | (9) |
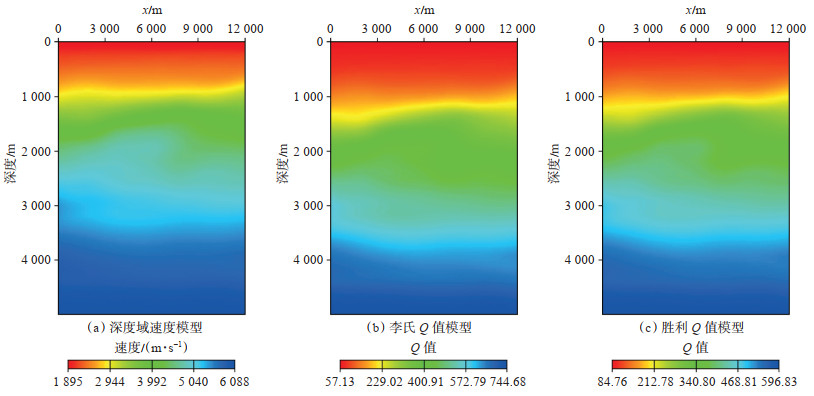
图 4为不同的Q值经验公式计算结果对比。胜利经验公式是对公式(7)的进一步细化和完善,由于该公式是针对胜利探区实际地质情况的经验总结,更符合胜利探区的实际,由这2种计算方法得出的Q值模型总体趋势是一致的[图 5]。
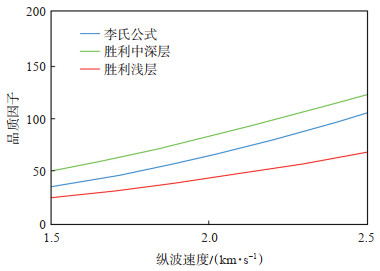
|
下载原图 图 4 不同的Q值经验公式计算结果对比 Fig. 4 Comparison of calculation results of empirical formulas with different Q values |
|
下载原图 图 5 胜利油田某探区速度模型和Q值模型 Fig. 5 Velocity model and Q model of an exploration area in Shengli Oilfield |
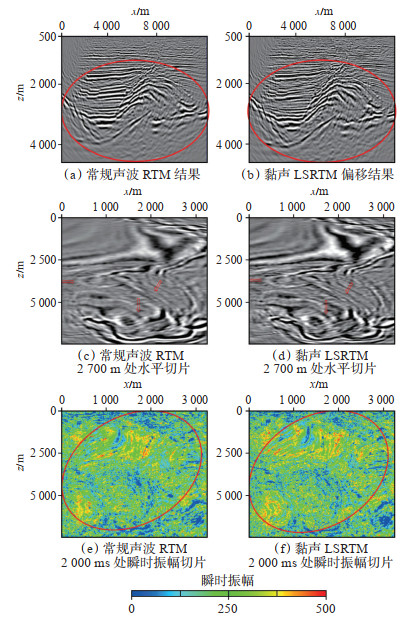
采用速度模型[图 5(a)]和应用胜利经验公式计算得到Q值模型[图 5(c)],分别进行常规声波逆时偏移和黏声最小二乘逆时偏移,其结果如图 6所示。应用黏声最小二乘逆时偏移对实际资料进行处理,共进行了10次偏移迭代,其成像质量较常规声波逆时偏移有一定的提升,在中、浅层同相轴的连续性增强,分辨率有所提升,断面信息更加丰富,成像精度有所提高,如图 6(a)和(b)中红色圈定部分所示。通过分析深度域水平切片,黏声最小二乘逆时偏移成像剖面能有效地刻画洼陷沉积区域砂砾岩边界,该方法处理的地震数据反映的内幕信息更加丰富,如图 6(c)和(d)中红色箭头所示。
|
下载原图 图 6 胜利油田某探区不同偏移结果及水平切片对比 Fig. 6 Comparison of different migration results and horizontal slices of an exploration area in Shengli Oilfield |
为了进一步分析其效果,将2种方法处理的深度域地震数据转换到时间域,然后分别求取了瞬时振幅,同时抽取瞬时振幅数据体的切片[图 6(e)—(f)],分析可知,黏声最小二乘逆时偏移比常规逆时偏移提取的瞬时振幅属性更加清晰,分辨率更高,这一结果将有助于后续岩性油气藏的有效识别。
为了分析计算效率,抽取实际资料中的某一单炮数据,分别应用基于CPU的程序和基于GPU并行加速的程序进行了黏声LSRTM处理(仅进行1次迭代),其计算效率如表 1所列。对比可见,单块TaslaK20 X相对于Xeon E5-2650中一个核加速比约为78.5。
|
|
下载CSV 表 1 CPU与GPU计算效率对比 Table 1 Comparison of CPU and GPU computing efficiency |
(1)吸收衰减补偿可以校正地震波的振幅和相位,对振幅的校正能够使中深层成像更加清楚,对相位的校正能够使成像分辨率得到提升,对分辨薄储层有利,这项技术是保幅处理的关键步骤之一。
(2)相对于常规逆时偏移(RTM),黏声最小二乘逆时偏移在衰减介质中进行黏性补偿,不仅能有效压制浅层噪音,而且能对地下弱照明区域进行照明补偿,提升了地震资料的分辨率,实现了真振幅成像,这对于岩性油气藏的勘探具有重要意义。
(3)基于GPU加速的黏声介质中最小二乘逆时偏移实现流程,相对于基于CPU的算法,效率大幅提升,解决了制约黏声最小二乘逆时偏移技术在实际生产中大规模实际应用的计算难题。
| [1] |
陈可洋. 逆时成像技术在大庆探区复杂构造成像中的应用. 岩性油气藏, 2017, 29(6): 91-100. CHEN K Y. Application of reverse-time migration technology to complex structural imaging in Daqing exploration area. Lithologic Reservoirs, 2017, 29(6): 91-100. |
| [2] |
陈可洋, 陈树民, 李来林, 等. 地震波动方程方向行波波场分离正演数值模拟与逆时成像. 岩性油气藏, 2014, 26(4): 130-136. CHEN K Y, CHEN S M, LI L L, et al. Directional one-way wave field separating numerical simulation of the seismic wave equation and reverse-time migration. Lithologic Reservoirs, 2014, 26(4): 130-136. |
| [3] |
TRAANTOLA A. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [4] |
TARANTOLA A. Theoretical background for the inversion of seismic waveforms, including elasticity and attenuation//AKI K, WU R S. Scattering and attenuation of seismic waves, Part Ⅰ. Basel: Birkhäuser, 1988: 365-399.
|
| [5] |
TARANTOLA A. Linearized inversion of seismic reflection data. Geophysical Prospecting, 1984, 32(6): 998-1015. DOI:10.1111/j.1365-2478.1984.tb00751.x |
| [6] |
BAMBERGER A, CHAVENT G, HEMON C, et al. Inversion of normal incidence seismograms. Geophysics, 1982, 47(5): 757-770. DOI:10.1190/1.1441345 |
| [7] |
NEMETH T, WU C, SCHUSTER G T. Least-squares migration of incomplete reflection data. Geophysics, 1999, 64(1): 208-221. DOI:10.1190/1.1444517 |
| [8] |
CHAVENT G, PLESSIX R. An optimal true-amplitude leastsquares pre-stack depth-migration operator. Geophysics, 1999, 64(2): 508-515. DOI:10.1190/1.1444557 |
| [9] |
刘梦丽, 徐兴荣, 王小卫, 等. 预条件弹性介质最小二乘逆时偏移. 岩性油气藏, 2020, 32(5): 133-142. LIU M L, XU X R, WANG X W, et al. Preconditioning elastic least-squares reverse time migration. Lithologic Reservoirs, 2020, 32(5): 133-142. |
| [10] |
刘桓, 苏勤, 曾华会, 等. 近地表Q补偿技术在川中地区致密气勘探中的应用. 岩性油气藏, 2021, 33(3): 104-112. LIU H, SU Q, ZENG H H, et al. Application of near-surface Q compensation technology in tight gas exploration in central Sichuan Basin. Lithologic Reservoirs, 2021, 33(3): 104-112. |
| [11] |
AKI K, RICHARDS P G. Quantitative seismology. San Francisco: W. H. Freeman & Co, 1980.
|
| [12] |
AKI K, BOUCHON M, REASENBERG P. Seismic source function for an underground nuclear explosion. Bulletin of the Seismological Society of America, 1974, 64(1): 131-148. DOI:10.1785/BSSA0640010131 |
| [13] |
AKI K. Analysis of the seismic coda of local earthquakes as scattered waves. Journal of Geophysical Research, 1969, 74(2): 615-631. DOI:10.1029/JB074i002p00615 |
| [14] |
MULDER W A, HAK B. An ambiguity in attenuation scattering imaging. Geophysical Journal International, 2009, 178(3): 1614-1624. DOI:10.1111/j.1365-246X.2009.04253.x |
| [15] |
HAK B, MULDER W A. Migration for velocity and attenuation perturbations. Geophysical Prospecting, 2010, 58(6): 939-951. |
| [16] |
王雪君, 任浩然, 江金生, 等. 基于点扩散函数的黏声介质反演成像. 石油物探, 2019, 58(1): 78-87. WANG X J, REN H R, JIANG J S, et al. Inversion imaging based on point spreading function for visco-acoustic medium. Geophysical Prospecting for Petroleum, 2019, 58(1): 78-87. |
| [17] |
李振春, 郭振波, 田坤. 黏声介质最小平方逆时偏移. 地球物理学报, 2014, 57(1): 214-228. LI Z C, GUO Z B, TIAN K. Least-squares reverse time migration in visco-acoustic medium. Chinese Journal of Geophysics, 2014, 57(1): 214-228. |
| [18] |
赵磊, 王华忠, 刘守伟. 逆时深度偏移成像方法及其在CPU/GPU异构平台上的实现. 岩性油气藏, 2010, 22. ZHAO L, WANG H Z, LIU S W. Reverse time migration method and its implementation on CPU/GPU heterogeneous platform. Lithologic Reservoirs, 2010, 22(Suppl 1): 36-41. |
| [19] |
MICIKEVICIUS P. 3D finite difference computation on GPUs using CUDA. Washington: Proceedings of 2nd Workshop on General Purpose Processing on Graphics Processing Units, GPGPU, 2009.
|
| [20] |
ZHANG M, SUI Z Q, WANG H Z, et al. Full waveform inversion on CPU/GPU heterogeneous platform and its application on land datasets. Beijing: 2014 International Geophysical Conference & Exposition, 2014.
|
| [21] |
郭振波, 李振春. 最小平方逆时偏移真振幅成像. 石油地球物理勘探, 2014, 49(1): 113-120. GUO Z B, LI Z C. True-amplitude imaging based on least-squares reverse time migration. Oil Geophysical Prospecting, 2014, 49(1): 113-120. |
| [22] |
CAUSSE E, URSIN B. Visco-acoustic reverse-time migration. Journal of Seismic Exploration, 2000, 9(2): 165-183. |
| [23] |
CHAVENT G, PLESSIX R E. An optimal true-amplitude leastsquares pre-stack depth-migration operator. Geophysics, 1999, 64(2): 508-515. |
| [24] |
崔宏良, 刘占军, 万学娟, 等. 拟合Q体建模技术及应用. 岩性油气藏, 2015, 27(3): 94-97. CUI H L, LIU Z J, WAN X J, et al. Application of fitting stereoscopic Q modeling technology. Lithologic Reservoirs, 2015, 27(3): 94-97. |
| [25] |
李庆忠. 走向精确勘探的道路. 北京: 石油工业出版社, 1993. LI Q Z. The way to precise exploration. Beijing: Petroleum Industry Press, 1993. |
 2022, Vol. 34
2022, Vol. 34



