2. 油气藏地质及开发工程 国家重点实验室(西南石油大学),成都 610599;
3. 中国石化西北油田分公司 油气开发管理部,乌鲁木齐 830001
2. State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610599, China;
3. Department of Oil and Gas Development Management, Sinopec Northwest Oilfield Company, Urumqi 830001, China
塔里木盆地顺托果勒低隆起上广泛发育有奥陶系碳酸盐岩断溶体油气藏,并显示出良好的开发潜力[1-4]。地质研究表明断溶体油藏储量较大,勘探开发前景较好[5-6]。断溶体油气藏无论在形态上,还是在储层特征上,都与常规砂岩油气藏和似层状的碳酸盐岩油气藏不同。在形态上,断溶体油气藏受多期次构造运动形成的走滑断裂控制,平面上沿断裂发育为长条形,纵向上有效厚度大,形态上呈“竖板”状;在储层性质上,有效储集空间为断裂形成的洞、缝系统且受应力控制具有明显的方向性,流体流动受储集空间的约束,也具有明显的方向性[7-9]。正因为这些特殊的油藏性质,目前通用的油藏工程方法直接在断溶体油藏中应用并不合适。为了弄清油藏的动态储量,通常采用流动物质平衡方法,通过结合产能方程,把物质平衡方程转化为利用流压数据来求取油藏的平均渗透率和动态储量[10-13],但该方法只适用于油气井位于正方形泄流区域中央的常规油藏[14-18],而断溶体油气藏的尺寸特征决定了井-藏位置关系发生了改变,必须探求适用于断溶体特征的流动物质平衡方法。
以充分的动、静态资料为基础,应用图示法分析断溶体油藏特殊的流动状态,并充分考虑其垂向流动的流态特征下不同井型对拟稳态产能的影响,建立流动物质平衡新方法,采用数值模拟方法验证新方法的适用性,最后将之应用于顺北油气田断溶体油气藏的现场实例,验证了新方法的实用性,以期为评价断溶体油藏动态储量提供依据。
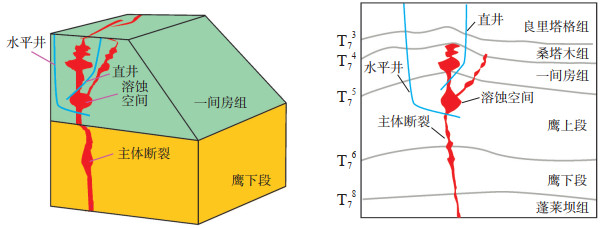
1 方法原理 1.1 油藏的几何模型断溶体油气藏受走滑断裂控制,在断裂带核部发育较大规模的洞穴,向两侧逐步发育裂缝-孔洞型、裂缝型储集体[19]。总体表现为纵向连通性较好,平面上沿断裂带呈不规则、断续状的条带分布,剖面上沿断裂带具有较明显的穿层性、不规则性以及不连续性,空间上呈“竖板”状特征[图 1(a)]。
|
下载原图 图 1 顺北油气田1号断裂带油藏模型(a)与典型油井纵向层位分布(b)[19] Fig. 1 Reservoir model(a)and vertical strata distribution of typical oil well(b)in No. 1 fault zone of Shunbei oil and gas field |
顺北油气田断溶体油藏含油区域宽度为100~ 400 m,井距为1 000~2 000 m,油藏的油柱高度为300~600 m[20]。直井WV通常布置在主断裂的核部,对油藏的高渗“甜点”区进行生产开发,“甜点”的同时生产开发[图 1(b)]。
1.2 流体的流动模式油藏的几何形态决定了断溶体油藏中不同生产井的特殊流动模式。对于普通砂岩层状油藏,直井的流动模式是平板内的常规径向流[图 2(a)],然而,在“竖板”状的断溶体油藏中[图 2(b)],直井位于核部,流动模式为“近井径向流+地层线性流”模式。从油藏侧视图也可以看出,断溶体油藏中的直井会出现较为明显的地层线性流模式[图 2(c)]。由此可知,断溶体油藏中直井流动模式与常规油藏中水平井的泄流模式接近。

|
下载原图 图 2 油藏内直井的流动特征示意图 Fig. 2 Sketch diagram showing flow regime of a vertical well in reservoirs |
同样地,对于普通砂岩层状油藏,水平井的流动模式主要为近井径向流+地层线性流[图 3(a)]。然而,断溶体油藏中的水平井横穿了断层的核部和翼部[图 3(b)],水平段的井筒在每个渗流体内的生产会出现较为明显的径向流[图 3(b)]。因此,断溶体油藏中水平井的流动方式反而更接近直井的泄流模式[图 3(b)]。在生产动态分析的时候,需要针对井的流动方式,选择对应的产能方程分析解释。

|
下载原图 图 3 油藏内水平井的流动特征示意图 Fig. 3 Sketch diagram showing flow regime of a horizontal well in reservoirs |
由于物质平衡方程使用时需要油藏的静压测试,而静压测试数据通常并不全面。因此,研究通常利用产能方程中井底流压、静压和产量的关系,将物质平衡方程中的静压用井底流压和产量替换,从而进行流动物质平衡的研究。由此可知,流动物质平衡方程的使用,需要油藏生产一定时间,油井进入稳态或是拟稳态流动阶段之后,方可使用。
油藏进入拟稳态生产阶段后,根据总压缩系数ceff的定义,总压缩系数可以通过储量、已采出量以及油藏压降(初始压力-油藏平均压力)表示为
| $ c_{\mathrm{eff}}=\frac{\mathrm{d} V_{\mathrm{fp}}}{V_{\mathrm{fp}} \mathrm{d} p_{R}}=\frac{N_{\mathrm{p}} B_{\mathrm{o}}}{N B_{\mathrm{oi}}\left(p_{\mathrm{i}}-p_{\mathrm{R}}\right)} $ | (1) |
式中:ceff为断溶体油藏的总压缩系数,10-4 MPa-1;Vfp为断溶体油藏的孔隙体积,m3;pi为油藏的初始压力,MPa;pR为油藏的平均压力,MPa;Np为断溶体油藏的累产油量,m3;N为断溶体油藏的动态储量,m3;Boi为初始条件下的油体积系数,m3/m3;Bo为压力pR的油体积系数,m3/m3。
因此,油藏的压降可以表示为
| $ p_{\mathrm{i}}-p_{\mathrm{R}}=\frac{B_{\mathrm{o}}}{c_{\mathrm{eff}} N B_{\mathrm{oi}}} N_{\mathrm{p}} $ | (2) |
而油藏平均压力与井底流压的差值可以通过产能公式表示为
| $ p_{\mathrm{R}}-p_{\mathrm{wf}}=q b_{\mathrm{pss}} $ | (3) |
式中:pwf为油井的井底流压,MPa;q为日产油量,m3/d;bpss为拟稳态流动条件下的系数,MPa·d/m3。
因此,油藏的初始压力与井底流压的差值为
| $ \Delta p=p_{\mathrm{i}}-p_{\mathrm{wf}}=p_{\mathrm{i}}-p_{\mathrm{R}}+p_{\mathrm{R}}-p_{\mathrm{wf}}=\frac{B_{\mathrm{o}}}{c_{\mathrm{t}} N B_{\mathrm{oi}}} N_{\mathrm{p}}+q b_{\mathrm{pss}} $ | (4) |
方程两边同除以Δpbpss,可以得到
| $ \frac{q}{\Delta p}=-\frac{B_{\mathrm{o}}}{c_{\mathrm{t}} N B_{\mathrm{oi}} b_{\mathrm{pss}}} \frac{N_{\mathrm{p}}}{\Delta p}+\frac{1}{b_{\mathrm{pss}}} $ | (5) |
根据式(5)可以通过回归
根据对流动特征的认识,断溶体油藏的直井需要对应常规油藏的水平井流动方式。因此,对于断溶体油藏的直井,流动物质平衡方法中bpss可以采用常规油藏水平井的拟稳态流动的产能方程。通过大量数据验证,直井的流动物质平衡方法推荐Chaudhry水平井产能模型,如式(6)所示:
| $ \frac{q_{\mathrm{o}}}{p_{\mathrm{R}}-p_{\mathrm{wf}}}=\frac{k h}{141.2 B_{\mathrm{o}} \mu_{\mathrm{o}}\left[\ln \left(\frac{r_{\mathrm{e}}}{r_{\mathrm{w}}}\right)-A C+s+s_{\mathrm{m}}+s_{\mathrm{CA}}-C^{\prime}\right]} $ | (6) |
式中:s为水平井或是增产导致的负压缩系数;sm为机械表皮,sCA是泄流形状导致的表皮因子;C'是形状转换常数;AC为泄流区域的形状参数;re为水平井的等效泄流半径,m,计算方法详见文献[21];rw为水平井的井径,m。对于AC的取值,0.75为原型泄流面积,0.738为长方形泄流面积。
Chaudhry模型中的参数具体取值可参考文献[21]中的详细叙述。断溶体油藏的水平井更接近于常规油藏中的直井流动。油井与油藏位置的配置关系符合直井位于正方形泄流区域中央的拟稳态产能方程
| $ b_{\mathrm{pss}}=\frac{141.2 B_{\mathrm{o}} \mu_{\mathrm{o}}}{k h}\left[\ln \left(\frac{r_{\mathrm{e}}}{r_{\mathrm{wa}}}\right)-\frac{3}{4}\right] $ | (7) |
式中:μo为原油的黏度,mPa·s;k为油藏的渗透率,mD;h为油藏厚度,m;re为油藏的泄流半径,m;rwa为等效井半径,m。等效半径是将酸化和压裂的增产作用等效为油井的负表皮,并等效为油井半径的处理方法。
由此可知,断溶体油藏流动物质平衡方法的理论基础可以表示为
| $ \left\{\begin{array}{l} \frac{q}{\Delta p}=-\frac{B_{\mathrm{o}}}{c_{\mathrm{t}} N B_{\mathrm{oi}} b_{\mathrm{ps}}} \frac{N_{\mathrm{p}}}{\Delta p}+\frac{1}{b_{\mathrm{pss}}} \\ b_{\mathrm{pss}}=\frac{141.2 B_{\mathrm{o}} \mu_{\mathrm{o}}}{k L}\left[\ln \left(\frac{r_{\mathrm{e}}}{r_{\mathrm{wa}}}\right)-\frac{3}{4}\right] \text { (水平井) } \\ b_{\mathrm{pss}}=\frac{141.2 B_{\mathrm{o}} \mu_{\mathrm{o}}}{k b}\left[\ln \left(\frac{r_{\mathrm{e}}}{r_{\mathrm{w}}}\right)-A C+S-C^{\prime}\right] \text { (直井) } \end{array}\right. $ | (8) |
式中:L为水平井水平段的长度,m;b为线性流宽度,m;S为3个表皮系数s,sm和sCA之和。
式(8)中直井、水平井的产能方程形态与常规油藏的水平井、直井产能方程一致,不同之处在于,针对断溶体特殊的“竖板”形状,对生产井的形状参数进了修正。水平井的拟稳态流动条件下的系数bpss里,常规方程中表示储层厚度h的部分,本文修正为断溶体中水平井的水平段长度L;而直井的拟稳态流动条件下的系数bpss表达式中,常规方程中储层厚度h被修正为断溶体油藏线性流的流动宽度b。
2 验证与讨论为了验证提出的断溶体直井和水平井的流动状态和流动物质平衡新方法中的渗透率计算公式,研究建立了反映断溶体油藏储层形态的数值模型,对生产井的流态和渗透率计算方法进行了研究,并对现场实例进行了分析讨论。
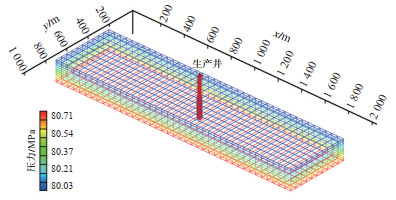
2.1 流态验证应用产量不稳定分析方法验证进入拟稳态前的流态特征。根据图 2(b)和图 3(b)的生产井特征,采用商用数值模拟器tNavigator,分别建立“竖板”状地层中央一口水平井、中央一口酸压水平井、中央一口直井,以及一口酸压直井4个数值模拟机理模型,模型参数如表 1所列。其中,断溶体的孔隙度为2%,水平井水平段长度200 m,直井生产段长度100 m,网格尺寸20 m×20 m×10 m,油藏机理模型如图 4所示。
|
|
下载CSV 表 1 模型参数设置 Table 1 Parameters setting in the model |
|
下载原图 图 4 机理模型网格系统示意图 Fig. 4 Sketch diagram showing grid system of mechanism model |
流体模型依据顺北1号断裂带中的流体PVT实验结果进行设置,油藏压力取88 MPa,油藏温度取150℃,原油黏度取0.25 mPa·s,原油初始体积系数取1.80 m3 / m3,油藏综合压缩系数ceff为40 × 10-4 MPa-1,为保障油井维持单相产出,井底流动压力限制为40 MPa。模拟十年生产动态历史,验证本文提出的断溶体油藏流动物质平衡方法的适用性和可靠性进行。
产量不稳定分析方法是一种基于压降试井模型的对油井生产历史的分析方法。该方法分为两部分,首先用产量修正压力(RNP)和物质平衡时间(tca)的关系绘制双对数诊断曲线,通过曲线的斜率判断油井处于的流动状态。特征斜率和压降试井中的斜率一致:径向流的斜率为0,线性流的斜率为1/2,边界控制流动的斜率为1。由于采用生产历史的时间间隔为天,因此产量不稳定分析中的流动诊断曲线并不能反映井储效应,仅能反映储层中的流动状态。在判断出油井的流动状态之后,选择油井进入边界流动之后的数据,进行流动物质平衡分析。
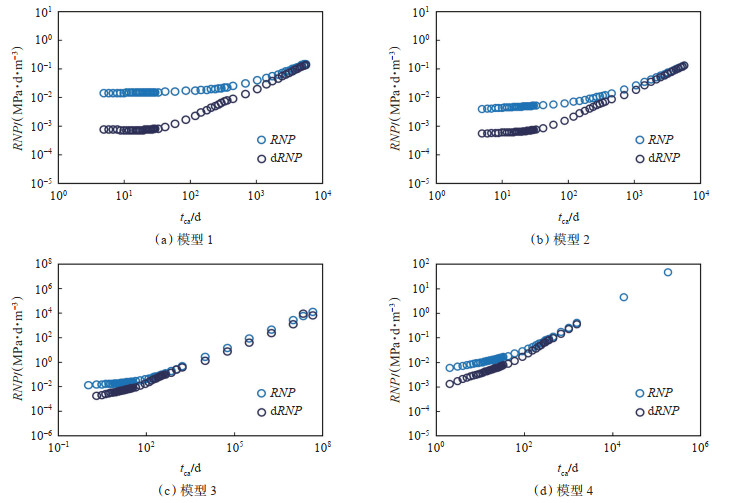
研究根据产量不稳定分析理论,计算数值模型生产历史的产量修正压力(RNP)和物质平衡时间(tca)的关系,绘制不稳定产量分析中的流动区域诊断图版(图 5),其中,RNP和tca的表达式为
| $ R N P=\frac{p_{\mathrm{i}}-p_{\mathrm{wf}}}{q_{\mathrm{o}}} $ | (9) |
| $ t_{\mathrm{ca}}=\frac{1}{B_{\mathrm{o}} q_{o}} \int B_{\mathrm{o}} q_{o} \mathrm{~d} t $ | (10) |
|
下载原图 图 5 机理模型流动曲线诊断曲线 Fig. 5 Diagnostic curves of mechanism models |
式中:RNP为产量修正压力,MPa·d/ m3;tca为物质平衡时间,d。
根据特征斜率可知,断溶体油藏水平井流动的前期以径向流(斜率为0)为主,后期转换为边界流动的特征(斜率为1);以日为计量单位的数据在不稳定产量诊断图版的RNP-tca和dRNP-tca关系图上并不能体现出酸压后的线性流特征[图 5(b)]。
其中,dRNP为RNP的导数曲线。
对于断溶体油藏直井,早期的流动显示以线性流(斜率为0.5)为主[图 5(c)],酸压会延迟边界流动的时间,但仍不能体现裂缝线性流特征[图 5(d)],最终转换为边界流动。
根据图 5可知,由于断溶体油藏特殊的“竖板”形状和井的位置关系,断溶体内的直井更加符合常规油藏水平井流动特征,而断溶体内的水平井更加接近于常规油藏直井的流动特征,数值模型的结果可以验证1.2节中提出的流动状态。
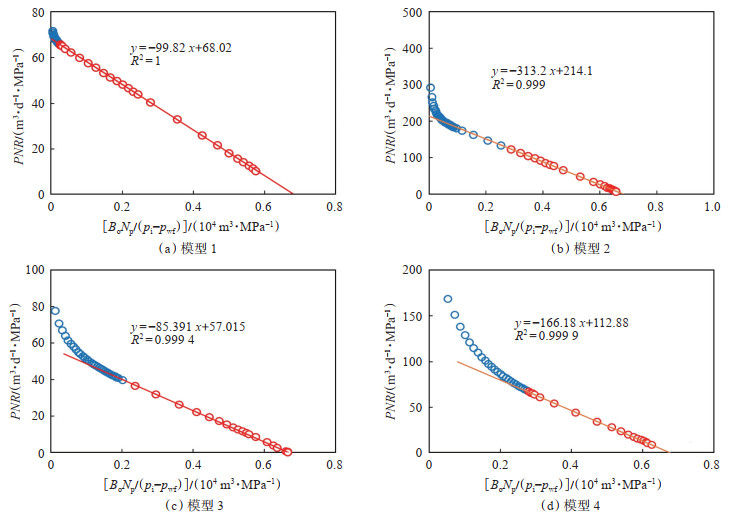
2.2 地层参数验证首先是应用3.1节所建机理模型的生产历史,对比流动物质平衡方法所计算的储量与物质平衡法计算储量的误差。根据式(8)得到的流动物质平衡计算方法,根据压力修正产量(PNR),做出流动物质平衡计算曲线(图 6),其中,PNR的表达式为
| $ P N R=\frac{q_{\mathrm{o}}}{p_{\mathrm{i}}-p_{\mathrm{wf}}} $ | (11) |
|
下载原图 图 6 机理模型流动物质平衡曲线 Fig. 6 Flowing material balance curves of mechanism models |
式中:PNR为压力修正产量,m3/(d·MPa)。
图 6中,对流动物质平衡曲线的直线段部分进行回归得到物质平衡方法[式(8)]中的斜率和截距,之后通过截距和斜率的表达式计算得到4个数值模拟机理模型的动态储量(表 2),与物质平衡方法计算结果分别相差0.34%,0.51%,3.0% 和1.3%,略小于物质平衡方法计算结果。其中,断溶体油藏物质平衡方法可以参考缝洞型油藏的物质平衡方法[22]。根据表 2可知,流动物质平衡方法对水平井的解释结果好于对直井的解释结果。
|
|
下载CSV 表 2 机理模型动态储量计算对比 Table 2 Comparison of dynamic reserve extracted from mechanism models |
根据式(8)中的bpss表达式,可以计算机理模型流动区域内的平均渗透率分别为9.72 mD,17.61 mD,9.33 mD和33.13 mD。对常规完井的水平井、直井机理模型,机理模型解释渗透率略小于模型设置的水平方向的渗透率(10 mD),这是由于模型的垂向厚度较大(100 m),垂向渗透率(2 mD)参与流动所致。而酸压后的机理模型解释渗透率大于机理模型设置值,这是因为流动物质平衡方法计算的是储层的平均渗透率,包含了储层的基准渗透率以及酸压带(水平100 mD和垂向20 mD)的高渗影响作用。
综上可知,本文建立的断溶体油藏流动物质平衡方法,在流动模式和参数提取精度上与数值模型计算的结果基本保持一致,数值模型验证了新方法对渗透率计算的可靠性。在完成流动状态和渗透率计算的验证之后,可以将本文的研究应用与现场数据的处理应用。
2.3 现场实例应用(1)SHB1-a井
SHB1-a是一口位于顺北1号断裂带上的直井。基于该井投产后的压力、产量数据,根据产量不稳定分析方法,做出流动曲线诊断图版(图 7)来判断流态。

|
下载原图 图 7 顺北油气田SHB1-a井流动物质平衡计算 Fig. 7 Flowing material balance calculation of well SHB1-a in Shunbei oil and gas field |
根据特征斜率可知,流动的前期为线性流,后期转为拟稳态边界流动。根据边界流动部分数值回归得到斜率、截距值[图 7(b)],应用本文推导的流动物质平衡方法计算有效渗透率32.66 mD,动态储量254.89万吨。
(2)SHB1-b井
SHB1-bH井是顺北1号断裂带上的一口水平井。应用产量不稳定分析方法处理压力、产量数据后得到流动曲线诊断图版,根据特征斜率可知,在进入拟稳态之前流体的流动为径向流特征[图 8(a)],与研究认识一致;按实际井位部署情况,该井所处断溶体长1 200 m,宽100 m,为了便于与试井结果比较,水平井地层厚度统一取为10 m。应用这套地层几何参数,对[图 8(a)]中的边界流动段应用本文提出的流动物质平衡方程[图 8(b)]计算储层参数,渗透率88.39 mD,动态储量459.52万t。渗透率与试井解释值66.3 mD基本一致。
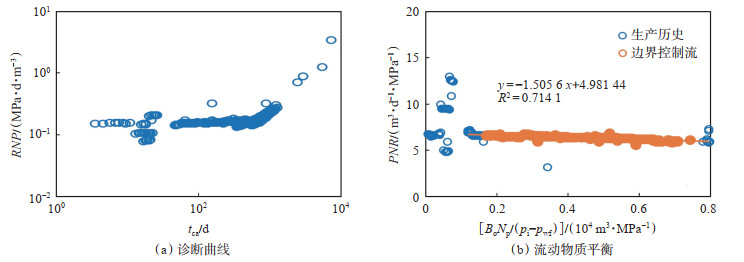
|
下载原图 图 8 顺北油气田SHB1-b井流动物质平衡计算 Fig. 8 Flowing material balance calculation of well SHB1-b in Shunbei oil and gas field |
SHB1-bH的流动物质平衡解释结果和其它油藏工程方法结果存在小幅差异(表 3)。动态储储方面,用于计算物质平衡的静压数据局限于投产后的36个月,而用于流动物质平衡的流压数据长达72个月,因而流动物质平衡得到的动态储量大于物质平衡方法得到的动态储量。
|
|
下载CSV 表 3 顺北油气田SHB1-b井流动物质平衡解释参数对比 Table 3 Comparison between flowing material balance method and other methods for well SHB1-b in Shunbei oil and gas field |
综合渗透率方面(表 2),流动物质平衡方法研究的对象是垂向上井筒径向流的平均渗透率[图 9(a)],即ky和kz的平均渗透率,试井渗透率则是按常规复合多区试井模型的水平方向渗透率的平均值,即kz和ky的平均值。
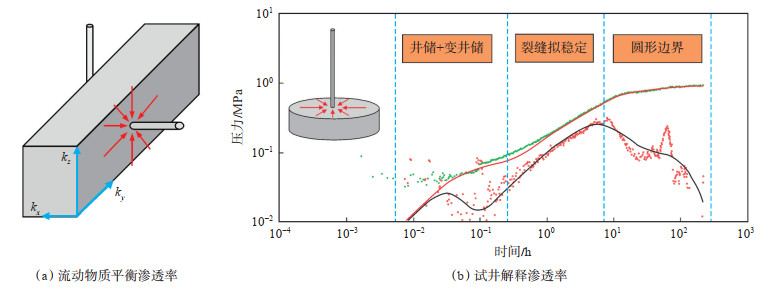
|
下载原图 图 9 顺北油气田流动物质平衡和试井渗透率对比 Fig. 9 Comparison of permeability between flowing material balance and well testing in Shunbei oil and gas field |
对于断溶体油藏,裂缝的垂向渗透率(kz)明显高于垂直于裂缝发育方向的渗透率(ky)。因此,流动物质平衡方法得到的储层渗透率大于试井解释得到渗透率。另外,流动物质平衡方法得到的储层渗透率,是流动区域内的平均渗透率,包括酸压增产带来的渗透率增加。本文研究对象是与断裂垂直或平行的水平井和直井,对于与断裂角度相交的斜井还需要进一步深化井藏位置与渗透率的校正关系。
3 结论(1)顺北油气田断溶体油藏直井的主要流动模式为地层线性流,水平井的流动模式更接近于径向流。建立的新方法对“竖板”状断溶体油藏的渗透率解释误差小于5%,动态储量的解释与物质平衡方法的解释结果较为接近。
(2)新方法采用拟稳态条件下水平井的产能方程来解决断溶体油藏直井的流动物质平衡渗透率提取问题,基于生产动态数据求解了顺北油气田断溶体油藏泄流范围内的平均渗透率和动态储量参数。
| [1] |
曹自成, 路清华, 顾忆, 等. 塔里木盆地顺北油气田1号和5号断裂带奥陶系油气藏特征. 石油与天然气地质, 2020, 41(5): 975-984. CAO Z C, LU Q H, GU Y, et al. Characteristics of Ordovician reservoirs in Shunbei 1 and 5 fault zones, Tarim Basin. Oil & Gas Geology, 2020, 41(5): 975-984. |
| [2] |
焦方正. 塔里木盆地顺托果勒地区北东向走滑断裂带的油气勘探意义. 石油与天然气地质, 2017, 38(5): 831-839. JIAO F Z. Significance of oil and gas exploration in NE strike-slip fault belts in Shuntuoguole area of Tarim Basin. Oil & Gas Geology, 2017, 38(5): 831-839. |
| [3] |
王素英, 张翔, 田景春, 等. 塔里木盆地顺北地区柯坪塔格组沉积演化及沉积分异模式. 岩性油气藏, 2021, 33(5): 81-94. WANG S Y, ZHANG X, TIAN J C, et al. Sedimentary evolution and sedimentary differentiation model of Silurian Kepingtage Formation in Shunbei area, Tarim Basin. Lithologic Reservoirs, 2021, 33(5): 81-94. |
| [4] |
王斌, 赵永强, 何生, 等. 塔里木盆地顺北5号断裂带北段奥陶系油气成藏期次及其控制因素. 石油与天然气地质, 2020, 41(5): 965-974. WANG B, ZHAO Y Q, HE S, et al. Hydrocarbon accumulation stages and their controlling factors in the northern Ordovician Shunbei 5 fault zone, Tarim Basin. Oil & Gas Geology, 2020, 41(5): 965-974. |
| [5] |
李红波, 王翠丽, 牛阁, 等. 有封闭水体的缝洞型油藏动态储量评价: 以塔里木盆地哈拉哈塘油田为例. 新疆石油地质, 2020, 41(3): 321-325. LI H B, WANG C L, NIU G, et al. Dynamic reserves evaluation of fractured-cavity reservoirs with closed water: A case from Halahatang Oilfield, Tarim Basin. Xinjiang Petroleum Geology, 2020, 41(3): 321-325. |
| [6] |
丛欣, 陈小凡, 乐平, 等. 油藏开发初期动态储量计算的生产指示曲线法研究. 重庆科技学院学报(自然科学版), 2019, 21(5): 11-14. CONG X, CHEN X F, YUE P, et al. Study on production indication curve method for dynamic reserve calculation in early stage of reservoir development. Journal of Chongqing University of Science and Technology(Natural Sciences Edition), 2019, 21(5): 11-14. DOI:10.3969/j.issn.1673-1980.2019.05.004 |
| [7] |
王建民, 张三, 杜伟, 等. 低幅度构造对特低渗透油藏油气水富集及开发动态的控制效应. 石油勘探与开发, 2019, 46(4): 728-738. WANG J M, ZHANG S, DU W, et al. The control effect of lowamplitude structure on oil-gas-water enrichment and development performance of ultra-low permeability reservoirs. Petroleum Exploration and Development, 2019, 46(4): 728-738. |
| [8] |
张晨朔, 韩征, 冯志刚, 等. 基于状态方程的溶解气回注油藏物质平衡计算方法. 科学技术与工程, 2020, 20(24): 9851-9855. ZHANG C S, HAN Z, FENG Z G, et al. Material balance equation calculations for solution gas reinjection reservoir with the equation of state. Science Technology and Engineering, 2020, 20(24): 9851-9855. DOI:10.3969/j.issn.1671-1815.2020.24.023 |
| [9] |
MATTAR L, ANDERSON D, STOTTS G. Dynamic material balance: Oil-or gas-in-place without shut-ins. The Journal of Canadian Petroleum Technology, 2006, 45(11): 7-10. |
| [10] |
YOU X T, JIA C S, LIU J Y, et al. A new production data analysis method of shale gas: Based on flowing material balance theory and considering the complex flow mechanisms of multiple pressure systems. Energy Procedia, 2019, 158: 3626-3632. DOI:10.1016/j.egypro.2019.01.900 |
| [11] |
HAN G F, LIU M, LI Q. Flowing material balance method with adsorbed phase volumes for unconventional gas reservoirs. Energy Exploration & Exploitation, 2019, 38(2): 519-532. |
| [12] |
XU Y M, ADEFIDIPE O, HASSAN D, et al. A flowing material balance equation for two-phase flowback analysis. Journal of Petroleum Science & Engineering, 2016, 142: 170-185. |
| [13] |
HE L, MEI H Y, HU X R, et al. Advanced flowing material balance to determine original gas in place of shale gas considering adsorption hysteresis. SPE Reservoir Evaluation & Engineering, 2019, 22(4): 1282-1292. |
| [14] |
蔡珺君, 唐青松, 欧家强, 等. 考虑水侵的异常高压气藏流动物质平衡. 断块油气田, 2019, 26(5): 596-600. CAI J J, TANG Q S, OU J Q, et al. Flow mass balance in overpressured gas reservoirs considering water influx. Fault-Block Oil & Gas Field, 2019, 26(5): 596-600. |
| [15] |
SUN Z, SHI J T, ZHANG T, et al. The modified gas-water two phase version flowing material balance equation for low permeability CBM reservoirs. Journal of Petroleum Science and Engineering, 2018, 165: 726-735. DOI:10.1016/j.petrol.2018.03.011 |
| [16] |
黄发木, 许明静. 流动物质平衡法在复杂气藏中的适用性研究. 重庆科技学院学报(自然科学版), 2016, 18(1): 25-27. HUANG F M, XU M J. Application of flowing material balance method in the calculation of reserves in complex gas reservoir. Journal of Chongqing University of Science and Technology (Natural Sciences Edition), 2016, 18(1): 25-27. |
| [17] |
吕心瑞, 刘中春, 朱桂良. 基于PDA方法的缝洞型油藏井控储量评价. 断块油气田, 2017, 24(2): 233-237. LYU X R, LIU Z C, ZHU G L. Well-controlled reserves evaluation of fracture vuggy reservoirs based on PDA method. Fault-Block Oil & Gas Field, 2017, 24(2): 233-237. |
| [18] |
朱桂良, 刘中春, 康志江. 缝洞型碳酸盐岩油藏大尺度试井新方法. 科学技术与工程, 2014, 14(13): 172-175. ZHU G L, LIU Z C, KANG Z J. The new method of large scale well test in fractured-vuggy carbonate reservoirs. Science Technology and Engineering, 2014, 14(13): 172-175. DOI:10.3969/j.issn.1671-1815.2014.13.033 |
| [19] |
刘哲. 顺北弱挥发性碳酸盐岩油藏合理开发方式研究. 成都: 成都理工大学, 2018. LIU Z. The reasonable development mode of weak volatile oil and carbonate reservoir in Shunbei zone. Chengdu: Chengdu University of Technology, 2018. |
| [20] |
黄鑫. 顺北地区中下奥陶统储层特征及成因研究. 成都: 成都理工大学, 2019. HUANG X. Characteristics and genesis of the Middle and Lower Ordovician reservoirs in the Shunbei area. Chengdu: Chengdu University of Technology, 2019 |
| [21] |
CHAUDHRY A U. Oil well testing handbook. Burlington: Gulf Professional Publishing, 2004: 44-84.
|
| [22] |
杨美华, 钟海全, 李颖川. 缝洞型碳酸盐岩油藏新型油藏生产指示曲线. 岩性油气藏, 2021, 33(2): 163-170. YANG M H, ZHONG H Q, LI Y C. New production index curve of fractured-vuggy carbonate reservoirs. Lithologic Reservoirs, 2021, 33(2): 163-170. |
 2022, Vol. 34
2022, Vol. 34




