低渗油气藏高效开发的基础在于对裂缝网络系统的研究和认识。裂缝不仅是流体的储集空间，还是流体渗流运移的通道^[1-2]。被裂缝沟通改造的基质网络渗流能力显著增强，极大地提高储层生产能力^[3-5]。裂缝发育的复杂性、极强的非均质性及各向异性使得裂缝表征和预测成为裂缝性油气藏勘探开发领域的世界性难题^[6]。20世纪80年代起，Baecher^[7]、Long等^[8]、Dershowitz等^[9]提出并完善的离散裂缝网络概念为裂缝的定量描述和建模提供了理论依据。在离散裂缝模型中，采用裂缝的几何特征，如裂缝产状、尺寸、开度、间距、发育密度等表征裂缝的三维空间特性。Ivanovai^[10]对于不同尺度的裂缝采取不确定性的方法来预测其分布。国内大多数裂缝分析还停留在单一因素对裂缝发育的影响上。许同海^[11]应用成像测井技术并辅以常规测井方法，计算裂缝的几何参数，进而评价裂缝的有效性；李志勇等^[12]应用主曲率法预测了江汉盆地王场地区裂缝发育情况；赵万金等^[13-14]则从地震资料出发，对小断裂和裂缝发育带进行了预测。部分学者对影响裂缝发育的多因素进行了分析。张亚春等^[15-16]结合成像测井、常规测井和地震资料建立了精细裂缝模型的思路和方法；黄辅琼等^[17]利用储层岩心裂缝进行定量观测与统计描述，结合测井，产能及构造分析，对储层双侧向测井中裂缝参数进行了标定；周新桂等^[18]探讨了在地质分析、储层裂缝数理统计、储层岩石参数实测和精细应力模拟等多学科基础上开展裂缝定量预测等；王建君等^[19]提出了基于地震几何属性的裂缝地震相识别和裂缝确定性提取及建模方法，综合应用地震倾角、曲率和非连续性等多属性，建立了高精度离散裂缝模型；王蓓等^[20]利用岩心照片、成像测井、叠前地震及动态监测等资料，定量表征了裂缝几何参数，并建立了多尺度非结构化的离散裂缝模型。从已有研究来看，不管是通过单因素还是利用多因素对裂缝进行分析，都存在未考虑不同尺度裂缝在开度、导流能力以及对油气运移的影响等方面的差异性，使得裂缝研究无法得出客观、全面的认识。

通过对塔里木盆地迪那2气田古近系裂缝的半定量描述，利用岩心分析、成像测井、地球物理、储层地质以及油藏动态等多学科资料，针对不同尺度裂缝的预测方法进行模拟，并以动态数据为依据优化静态裂缝模型，以期建立一套行之有效的裂缝预测新方法。

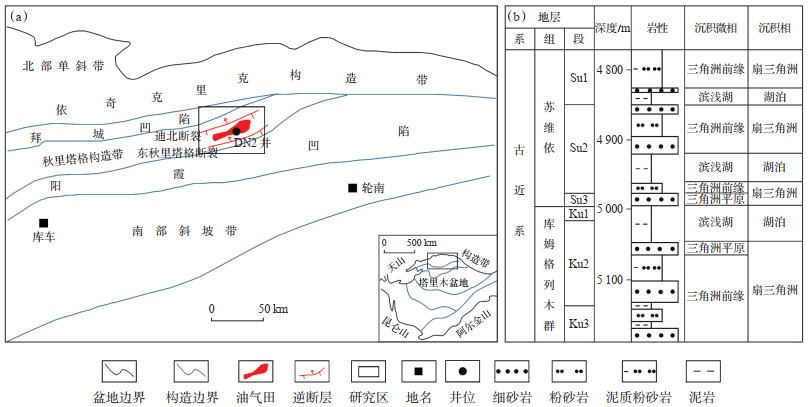
迪那2气田构造位于库车前陆盆地秋里塔格构造带东部迪那—东秋构造区带上（图 1），为一受南、北2条北东东走向的北倾逆冲断层所夹持的东西向展布的长轴背斜。该背斜南翼断层断距大、延伸长，北翼断层发育少，核部多发育小断距断层，且多为逆断层。由于应力作用，研究区同时发育了3个正断层带，分别为1条地堑带和2条单向正断层带（北翼正断层带和南翼正断层带）。该区主要含气层系为古近系，自下而上发育库姆格列木群组（Ek）和苏维依组（E₃s），厚度为334~408 m，主力产气层为Su1段和Su3段，次产气层为Su2段、Ku2段和Ku3段，Ku1段为区域隔夹层，厚度为10~90 m。迪那地区古近系沉积以扇三角洲前缘亚相为主，扇三角洲平原亚相发育较少，前缘亚相中以水下分流河道、分流河道间、河口坝微相为主，局部地区发育湖泊相，岩性为滨浅湖亚相的滨浅湖泥。储层岩性主要为褐色粉砂岩、中—细砂岩，次为杂色-褐色泥质粉砂岩、泥岩，少量砾岩。岩石类型以岩屑砂岩为主，其次为次长石岩屑砂岩。分选中—好，多为次棱—次圆状，颗粒以点-线接触为主，孔隙式胶结为常见胶结方式。迪那2气田为受背斜构造控制的异常高压块状底水凝析气藏，气水界面海拔为-3 712 m。

图 1

Fig. 1

下载原图 图 1 塔里木盆地迪那2气田构造位置（a）及古近系岩性地层柱状图（b） Fig. 1 Tectonic location(a)and stratigraphic column of Paleogene(b)in Dina-2 gas field, Tarim Basin

为了做好多信息离散裂缝表征，准确收集不同信息的裂缝数据是至关重要的一步。定量描述的裂缝信息越准确，所建立的离散裂缝模型就越能反映真实的地质情况^[21]。本次研究采用的多信息裂缝表征方法主要包括岩心分析、成像测井、地球物理、油藏动态等。

岩心分析是最直观、最可靠的研究裂缝的方法。依据岩心裂缝发育特征对地层裂缝进行分析，可以得出裂缝的几何特征（产状、长度、开度、密度、间距等）、充填情况、力学性质、裂缝成因及裂缝发育影响因素等重要认识^[22-23]。迪那2气田目的层段取心井5口，用于裂缝分析的岩心样品95块，薄片样品281块（表 1）。

表 1(Table 1)

表 1 塔里木盆地迪那2气田取心井岩心裂缝几何特征参数统计 Table 1 Geometric parameters of core fractures from coring wells in Dina-2 gas field, Tarim Basin 井名 样品数量/块 倾角统计/% 平均真开度/mm 平均线密度/（条·m-1） 平均面密度/（条·m-2） 填充情况/% 岩心 薄片 15°~45° 45°~75° 75°~90° 宏观 微观 全充填 半充填 未充填 宏观 微观 宏观 微观 宏观 微观 DN205H 25 45 0 22 78 0.48 0.035 0.85 0.029 44.1 0 18.5 4.5 37.4 95.5 DN204 18 66 0 0 100 0.50 0.029 0.63 0.035 78.6 0 20.3 5.6 1.1 94.4 DN202 9 70 0 41 59 0.41 0.045 0.65 0.031 48.3 24.8 36.5 11.5 15.2 63.7 DN201 30 56 8 58 34 0.39 0.044 0.47 0.027 28.6 5.8 35.5 16.3 35.9 77.9 DN22 13 44 3 24 73 0.53 0.032 1.05 0.032 52.3 7.8 32.6 6.9 15.1 85.3 合计 95 281 2 29 69 0.46 0.037 0.73 0.031 50.4 7.7 28.7 8.9 20.9 83.4

下载CSV 表 1 塔里木盆地迪那2气田取心井岩心裂缝几何特征参数统计 Table 1 Geometric parameters of core fractures from coring wells in Dina-2 gas field, Tarim Basin

（1）裂缝产状。裂缝产状是裂缝方向性的描述量，在三维空间中，裂缝产状通常由裂缝断面的走向（或倾向）和倾角来定义。裂缝按照倾角大小可分为水平缝（0°~15°）、低角度斜交缝（15°~45°）、高角度斜交缝（45°~75°）和垂直缝（75°~90°）等4类^[24]。从岩心观察来看，迪那2气田古近系发育有各种倾角的裂缝，但多数裂缝倾角为45°~90°，即以高角度斜交缝（占比为29%）和垂直缝（占比为69%）为主。由于部分岩心受破坏严重，裂缝倾向难以准确观测。

（2）裂缝长度。裂缝长度主要影响储层基质与裂缝之间的连通性。裂缝越长，越容易形成相互渗流的裂缝网络，从而构成油气的运移通道。目前还没有精确测量裂缝长度的有效方法，而岩心大多被裂缝切穿，因此也无法直观观测到裂缝的真实长度。

（3）裂缝开度。裂缝开度是表征裂缝张开程度的量，也是裂缝物性计算的重要参数，开度的大小反映裂缝发育的规模。在实际研究中，无论是通过岩心观察的宏观裂缝，还是镜下岩石薄片统计的微观裂缝，其裂缝开度都要比真实裂缝开度大，因此需要对观测的开度值进行必要的修正^[25]。经验修正公式为

式中：A_t为裂缝真开度，mm；A_a为裂缝视开度，mm；θ为测量面与裂缝面夹角，（º）。

从研究区岩心观察的统计结果来看（表 1），一半以上的宏观裂缝真开度小于0.460 mm，3/4的微观裂缝真开度小于0.037 mm。

（4）裂缝密度。裂缝密度是反映裂缝密集程度的值，是裂缝表征的重要参数之一，也是评价裂缝发育程度的重要指标之一，可定义为单位长度、单位面积或单位体积内裂缝的条数。根据裂缝维度的不同，裂缝密度可分为线密度（P₁₀）、面密度（P₂₁）和体密度（P₃₂）^[26-29]。在岩心分析和镜下岩石薄片研究中，裂缝密度的表征方法主要为计算P₁₀和P₂₁，其中，P₁₀的计算公式为

P₂₁的计算公式为

式中：N为裂缝总条数，条；L为统计裂缝总长度，m；A为测量区域横截面积，m²。

统计结果表明，研究区内裂缝总体较为发育，各井裂缝发育程度变化不大，岩心线密度均值为0.73条/m，薄片裂缝面密度均值为0.031条/m²。

（5）裂缝间距。裂缝间距指的是同一组系裂缝之间的垂直距离，和裂缝线密度成倒数关系。裂缝间距越小，裂缝密度越大，裂缝就越密集。本区的宏观裂缝间距较难直接观测和统计，只有极少数裂缝发育的密集段能测出裂缝间距。

（6）裂缝充填情况。裂缝充填程度可划分为全充填、半充填和未充填3类。岩心观察表明，目的层段充填程度较高，充填物以泥质、方解石和石膏最为常见。迪那2气田取心段宏观裂缝平均充填程度达79.1%，即多数为无效缝，其中全充填裂缝约占50.4%，半充填裂缝约占28.7%，未充填裂缝占20.9%。从镜下岩石薄片来看，目的层段充填程度较低，半充填裂缝平均约占83.4%，全充填缝和未充填缝相对不发育，仅占所有裂缝的16.6%。宏观裂缝与微观裂缝充填程度的差异表明，微裂缝在改善储层渗透性方面起主要作用。

（7）裂缝形态及成因。不同力学性质裂缝的形态具有较大差别。张性裂缝常呈不规则折线状，剪裂缝常呈规则的直线状，张扭性裂缝则呈较规则的直线、折线状或成组的斜列状。裂缝成因归纳起来主要有构造作用、剝蚀作用、成岩作用、古岩溶作用、溶蚀塌陷、压实作用、撞击作用等多种。通过岩心（图 2）观察，研究区内目的层段裂缝大多为剪裂缝，缝面平直规则且成组出现，可见擦痕和阶步，表明迪那地区裂缝成因主要与局部构造变形及断裂作用有关。

图 2

Fig. 2

下载原图 图 2 塔里木盆地迪那2气田古近系岩心照片 （a）剪切缝，缝面见擦痕，DN202，5 023.35 m；（b）剪切缝，缝面见擦痕，DN22，4 917.99 m；（c）共轭裂缝，DN205H，5 321.56 m Fig. 2 Core photos of Paleogene in Dina-2 gas field, Tarim Basin

测井资料具有信息丰富全面、垂向分辨率高等特点，是用于研究裂缝的主要基础资料之一。测井新技术，尤其是微电阻率成像测井的大规模应用，使得对裂缝的识别更加准确（图 3）。迪那2气田具有丰富的电阻率成像资料，共28口井目的层段具有成像裂缝解释数据。

图 3

Fig. 3

下载原图 图 3 塔里木盆地迪那2气田裂缝成像测井响应特征 （a）高角度共轭缝，DN205H，5 319~5 324 m；（b）高角度平行缝，DN204，5 017~5 020 m Fig. 3 Response characteristics of fracture imaging logging in Dina-2 gas field, Tarim Basin

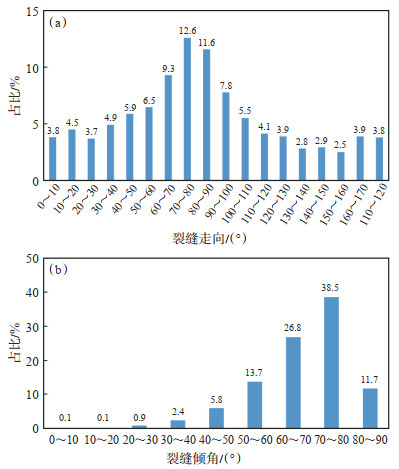
从统计结果来看，裂缝走向主要为60°~100°（近东西向，占比为41.3%）和0°~20°，150°~180°（近南北向，占比为18.5%）（图 4a），裂缝倾角特征较为明显，主要为50°~85°（图 4b）。总体上，迪那地区裂缝走向为近东西向，发育高角度斜交缝和垂直缝。

图 4

Fig. 4

下载原图 图 4 塔里木盆地迪那2气田取心井成像裂缝走向（a）和倾角（b）统计 Fig. 4 Histogram of imaging fracture strike(a)and dip angles(b)in Dina-2 gas field, Tarim Basin

鉴于裂缝的复杂性和特殊性，采用单一手段或从某一侧面来预测裂缝往往具有很大的局限性^[30]，因此想要得到准确、全面的裂缝认识，就需要开展多信息、分级次的综合裂缝预测研究。根据裂缝发育的规模和尺度，可将构造裂缝系统划分为3类，即大尺度裂缝、中等尺度裂缝和小尺度裂缝。大尺度裂缝为地震资料上直接识别的断层^[31]，中等尺度裂缝为次一级规模的断层，小尺度裂缝在地震资料上不能直接识别，只能通过岩心和成像测井资料分析得到。对于小尺度裂缝的井间预测，则需要综合应用多种研究手段，从地球物理、沉积储层到生产动态多信息综合分析。

天然构造裂缝会造成地层的各向异性，地震波在含裂缝的岩层中传播时，其运动学属性和动力学属性也会发生有一定规律的变化^[32]。通过对各类地震属性体的研究能挖掘出其中所携带的裂缝信息^[33]。针对裂缝预测，常用的地震属性众多，主要包括曲率、相干体、方位角和倾角、混沌体、方差体、蚂蚁体、AVO属性等，但不同地区的应用效果也存在差异。通过对各类反映裂缝分布规律的地震属性体的对比分析，发现塔里木盆地迪那2气田裂缝在曲率和蚂蚁体地震属性上有较好的响应。

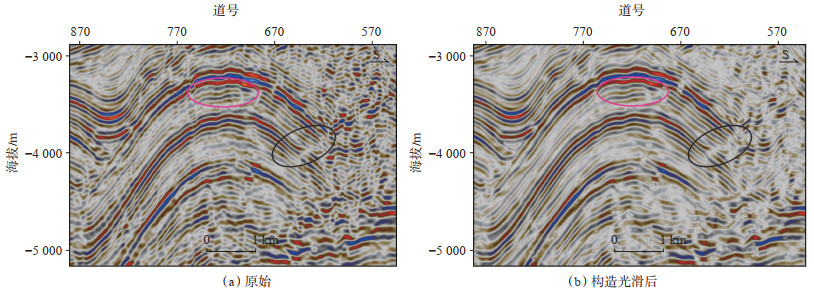
在利用地震属性体进行裂缝分布规律预测前，需要对原始地震数据体进行预处理，去除原始地震资料中的随机噪声，增强地震同相轴的横向连续性，并保留断层、裂缝等边界信息。本次研究选用构造光滑方法对原始地震数据体进行预处理，处理后的数据地层连续性变好，断裂信息更明显（图 5）

图 5

Fig. 5

下载原图 图 5 塔里木盆地迪那2气田三维地震资料预处理前后剖面对比 Fig. 5 Comparison of 3D seismic data before and after preprocessing in Dina-2 gas field, Tarim Basin

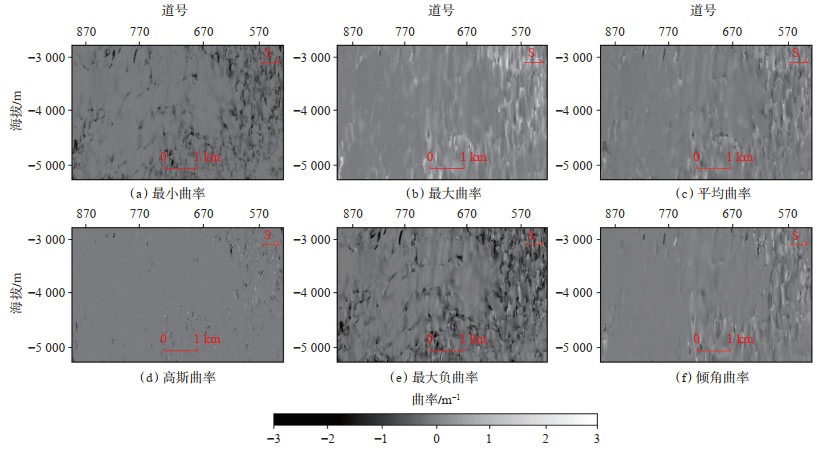
曲率是地震构造属性中的一种，对断裂和裂缝响应敏感。从构造应力角度出发，当地层发育断层或裂缝时，在地震数据体相应位置上会出现曲率异常。常用的曲率属性体有最大曲率、最小曲率、高斯曲率、平均曲率、倾角曲率、最大正曲率、最小负曲率等。从多种曲率模拟的结果（图 6）来看，最小曲率法在研究区的应用效果较好，最大曲率和平均曲率次之，最大负曲率噪声太多，倾角曲率分辨率低，高斯曲率效果最差。

图 6

Fig. 6

下载原图 图 6 塔里木盆地迪那2气田多种曲率地震属性 Fig. 6 Comparison of different curvatures in Dina-2 gas field, Tarim Basin

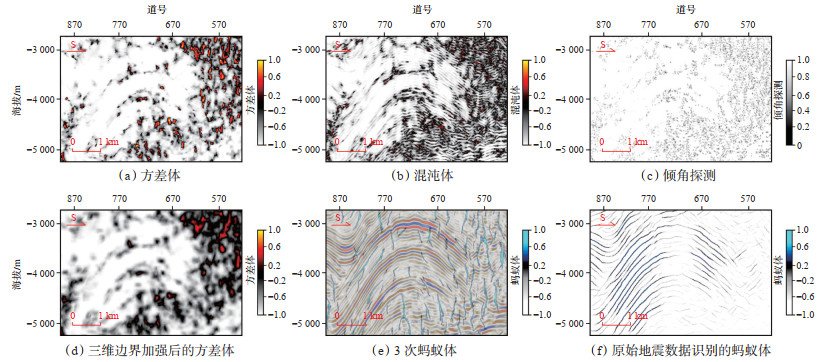
蚂蚁算法最早由Dorigo等^[34]于1996年提出，是利用“电子蚂蚁”间的信息交流求解组合优化目标的一种仿生算法。后来由Pedersen等^[35]首次将该算法应用于断层和裂缝的追踪识别。理论上任何地震数据体都可以作为蚂蚁追踪的输入，但是输出的质量千差万别。研究发现，采用经过边界探测处理的数据体作为输入可更好地展示断层带或裂缝带发育位置，从而提高蚂蚁体追踪的准确度。常用的边界探测方法有提取混沌体、方差体、倾角偏差体等。通过对比，利用方差体进行边界探测效果最好（图 7a），混沌体（图 7b）包含了太多地层信息，倾角探测（图 7c）识别断层连续性差。为了使后续断层及裂缝的识别更加精确，还需要利用三维边界增强技术进一步提高数据体的连续性、分离不同信号。三维边界增强后的方差体（图 7d）边界更突出、噪音更少，信噪比明显提高。在利用蚂蚁追踪进行裂缝和断层识别时，需要设定“电子蚂蚁”的搜索范围和方向来估算断层。采用运算3次蚂蚁体的方式，即积极蚂蚁-消极蚂蚁-积极蚂蚁，其结果（图 7e）与原始地震数据体（图 7f）相比，3次蚂蚁体对断层和裂缝的识别度明显提高，而直接使用原始数据体进行蚂蚁体属性提取的结果则非常糟糕，几乎无法识别断层和裂缝。

图 7

Fig. 7

下载原图 图 7 塔里木盆地迪那2气田蚂蚁体识别断层（裂缝）方法对比 Fig. 7 Comparison of fault (fracture) identification methods by ant-tracking technology in Dina-2 gas field, Tarim Basin

从岩心、薄片和成像测井解释的裂缝资料来看，不同层位的裂缝发育程度差异很大。为了弄清裂缝发育规律，需要对影响研究区裂缝发育的沉积储层因素进行分析。

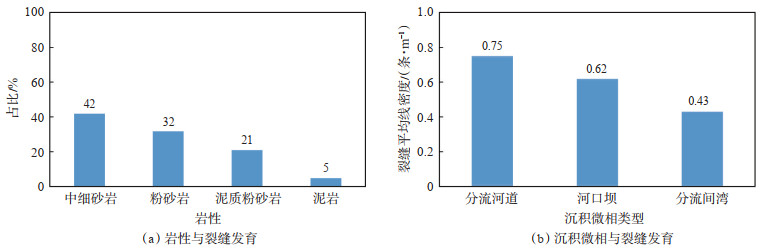
不同的岩石类型因其成分、结构和构造不同，力学性质各异，在相同的构造应力作用下，裂缝发育程度也存在差异。一般脆性强的岩石容易发生破裂且具有较高的裂缝密度。通过裂缝发育程度的统计发现，不同岩性裂缝发育程度具有明显差异。整体而言，中细砂岩中裂缝最发育，其次是粉砂岩、泥质粉砂岩，泥岩相对不容易形成裂缝（图 8a）。裂缝发育程度与沉积体系也存在相关性，统计结果表明，扇三角洲相中裂缝发育程度高于湖泊相中，而在相同沉积相中，各微相裂缝密度大小顺序为：分流河道＞河口坝＞分流间湾（图 8b）。

图 8

Fig. 8

下载原图 图 8 塔里木盆地迪那2气田沉积储层与裂缝发育关系 Fig. 8 Relationships of fracture development with lithologies and sedimentary microfacies in Dina-2 gas field, Tarim Basin

国内外诸多学者对构造裂缝的发育程度与单层厚度的关系进行了研究，普遍认为在一定的范围内，裂缝的线密度与单层厚度存在较明显的负相关。即当其他岩石参数和所受应力条件相同时，薄层岩石中的裂缝较发育^[36-39]。袁静等^[40]研究发现，迪那地区岩层厚度与其平均裂缝线密度关系整体上呈“座椅式”负相关，层厚为1~4 m时，裂缝密度下降较快；层厚为4~8 m时，裂缝密度下降幅度变小；层厚为8~12 m时，裂缝密度再次快速降低。

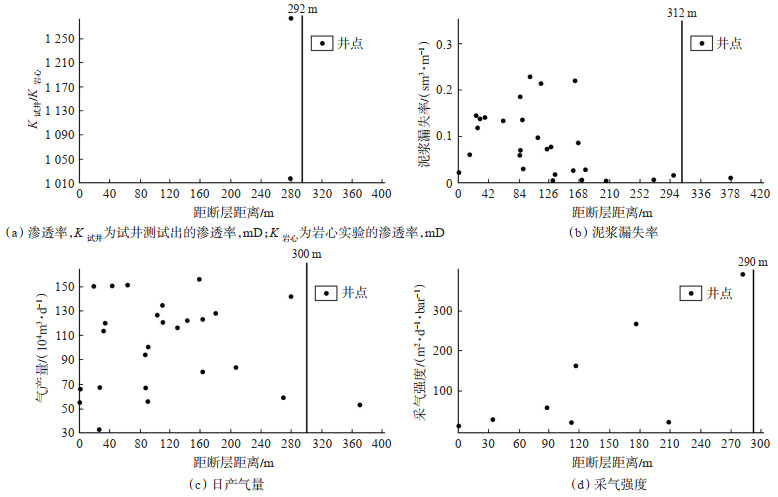
由于断层两盘地质体的相对运动，在断层附近会产生应力扰动，沿断层具有明显的应力集中现象，裂缝明显发育，随着与断层距离的增大，裂缝发育程度具有依次递减的趋势^[41-42]。动态分析就是通过对渗透率（K）、泥浆漏失、生产数据、采气强度等参数进行技术分析，计算得到断层影响周围裂缝发育的距离。在距断层290 m左右有2口井试井渗透率大（图 9a），泥浆漏失的井大多位于距断层小于310 m的范围内（图 9b），日产气高的井大部分位于距断层300 m以内的范围（图 9c），从采气强度和距断层距离关系来看，气井大多位于距断层小于290 m的范围内（图 9d），综合研究认为断层影响周围裂缝发育的最大距离为300 m左右。

图 9

Fig. 9

下载原图 图 9 塔里木盆地迪那2气田断层影响裂缝发育的距离分析 Fig. 9 Influence of distance from fault on fracture development in Dina-2 gas field, Tarim Basin

在综合各类动、静态信息基础上进行气藏地质建模工作，主要开展了构造建模、沉积相建模、孔隙度建模、渗透率建模及储量计算等研究工作。

构造模型反映储层的空间格架，是地层建模、沉积相建模以及储层物性建模的基础。为了最大限度提高网格质量，将边界设定为矩形，长轴方向为区域大断裂秋里塔格断裂和迪北断裂的走向（79°），总面积为124.3 km²，网格规模为191×28×271（I×J×K），共计1 449 308个网格点，主力层位Su1和Su3段垂向网格平均厚度为1 m左右，其余层位垂向厚度为10 m。根据模型网格质量标准，该构造模型网格质量高，不存在角度尖锐网格、负体积、负厚度以及扭曲网格（表 2），能够满足沉积微相建模和储层物性建模研究的各项需求。

表 2(Table 2)

表 2 塔里木盆地迪那2气田构造模型网格质量检查表 Table 2 Grid quality check list of construction model in Dina-2 gas field, Tarim Basin 网格参数 最小值 最大值 平均值 标准差 角度偏差/（°） 0 10.40 0.67 0.56 体积/m3 256.00 4 427 527.00 117 784.00 128 175.00 厚度/m 0.10 25.69 2.94 3.20 扭曲度/（°） 0 0 0 0

下载CSV 表 2 塔里木盆地迪那2气田构造模型网格质量检查表 Table 2 Grid quality check list of construction model in Dina-2 gas field, Tarim Basin

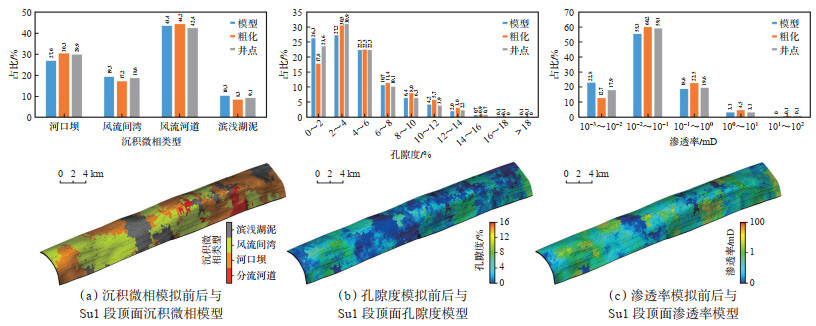
（1）沉积微相建模。迪那2气田优质储层主要发育于各层序的水侵体系域和高位体系域早期，以扇三角洲分流河道和河口坝砂体为主，储集性能相对较好，储层侧向分布较为稳定；席状砂次之；泛滥平原主要为区域隔夹层，储集性能差。本次研究首先粗化单井沉积微相数据，然后对沉积微相垂向比例进行控制，平面上利用沉积微相趋势图作为约束，采用序贯指示模拟方法，最后模拟得到沉积微相模型（图 10a）

图 10

Fig. 10

下载原图 图 10 塔里木盆地迪那2气田地质模型参数对比 Fig. 10 Comparison of geological model parameters in Dina-2 gas field, Tarim Basin

（2）相控储层物性建模。储层物性模拟前，需要对孔隙度和渗透率曲线进行粗化，单井孔隙度数据采用算术平均法，渗透率采用调和平均法，两者都以沉积微相作为权重约束。孔隙度属性模拟采用序贯高斯随机模拟方法，辅以沉积相属性作为第2变量进行约束，模拟得到孔隙度模型。由于渗透率与孔隙度存在一定的相关性，因此将模拟得到的孔隙度模型作为第2变量约束进行渗透率属性模拟。从物性模拟前后对比来看，孔隙度和渗透率数据基本保持一致（图 10b），整体上能客观反映迪那2气田地质特征（图 10c）。

本次储量计算采用容积法，孔隙度大于6%且渗透率大于0.05 mD时，网格为有效储层网格，气水界面海拔为-3 712 m，含气饱和度在气水界面之上平均为65%。容积法计算公式：

式中：N_g为天然气地质储量，108 m3；A为含气面积，km²；h为气层有效厚度，m；φ为气层孔隙度，%；S_g为含气饱和度，%；B_gi为气体体积系数。

本次模型计算天然气地质储量为1 600×10⁸ m³，与探明地质储量比相对误差仅为-1% 左右。

裂缝分析是对所有井上的裂缝进行分组分析，对每组裂缝分岩相进行数据统计，得到其裂缝产状及相关参数值，可以很好地显示裂缝组在每口井上分布的疏密程度。裂缝的形成基本上受控于地层应力场，天然构造裂缝的走向与主应力密切相关。对于构造运动复杂的区域，可能还会存在多种不同走向的裂缝，由于这些不同走向的裂缝在尺度、开度以及规模上都不一致，在裂缝分析时需要对裂缝进行分组。结合已分析的迪那2气田成像裂缝发育特征，将裂缝分为近东西走向和近南北走向2组。

裂缝的发育程度与岩性（相）或某种地层属性密切相关，而且对于不同期次、不同走向裂缝，相关性也不尽相同。相控（岩相）需要针对不同分组的裂缝进行分析，这与地质建模中进行属性建模时相控的原理一致。通过岩性与裂缝发育关系分析可知，中细砂岩和粉砂岩中裂缝最发育。本次裂缝密度计算分2种岩相进行，即中细砂岩和粉砂岩为一组（砂岩组），泥质粉砂岩和泥岩（泥岩组）为一组。从计算结果（表 3）可以看出，东西向裂缝组的裂缝明显比南北向裂缝组的更发育，同一走向的裂缝，砂岩组裂缝密度大于泥岩组。

表 3(Table 3)

表 3 塔里木盆地迪那2气田不同裂缝组裂缝发育程度对比 Table 3 Comparison of fracture development degree of different fracture groups in Dina-2 gas field, Tarim Basin 裂缝密度/（条·m-1） 东西向裂缝/条 南北向裂缝/条 泥岩组 砂岩组 合计 泥岩组 砂岩组 合计 0~0.1 838 5 367 6 205 390 898 1288 0.1~0.2 258 1 661 1 919 157 322 479 0.2~0.3 111 1 161 1 272 84 212 296 0.3~0.4 47 592 639 40 123 163 0.4~0.5 45 409 454 34 127 161 0.5~0.6 18 186 204 21 87 108 0.6~0.7 12 130 142 15 85 100 0.7~0.8 6 98 104 8 48 56 0.8~0.9 2 37 39 3 39 42 0.9~1.0 2 16 18 3 29 32 1.0~1.1 2 13 15 2 20 22 1.1~1.2 0 14 14 2 17 19 1.2~1.3 0 8 8 3 9 12 1.3~1.4 0 3 3 0 13 13 1.4~1.5 0 2 2 0 9 9 1.5~1.6 0 2 2 0 6 6 1.6~1.7 0 1 1 0 2 2 合计 1 341 9 700 11 041 762 2 046 2 808

下载CSV 表 3 塔里木盆地迪那2气田不同裂缝组裂缝发育程度对比 Table 3 Comparison of fracture development degree of different fracture groups in Dina-2 gas field, Tarim Basin

在对裂缝发育宏观认识的基础上，结合影响裂缝发育因素，如构造曲率、蚂蚁体、距断层距离等，分析不同属性体与裂缝发育的相关性，计算权重系数，并对不同权重的属性体进行体融合，最后通过融合后的属性体约束建立裂缝密度属性场。将不同属性体的值采样到单井上，与单井成像解释的裂缝密度曲线做线性判别分析，得到不同属性体的权重系数（表 4）。在东西走向的砂岩裂缝组中，距断层距离属性对融合属性体的影响最大，其次为最小曲率和蚂蚁体，而在泥岩组中影响最大的是孔隙度，其次为距断层距离，最小为蚂蚁体属性；在南北向裂缝组中，最小曲率和孔隙度分别对砂岩组和泥岩组融合属性体的贡献最大。

表 4(Table 4)

表 4 塔里木盆地迪那2气田融合属性体相关性分析权重系数统计表 Table 4 Weight coefficient statistics of correlation analysis of fusion attribute volume in Dina-2 gas field, Tarim Basin 裂缝组 岩性组 权重系数 岩相 最小曲率 距断层距离 孔隙度 蚂蚁体 东西走向裂缝 砂岩组 0.11 0.22 0.27 0.18 0.22 泥岩组 0.16 0.19 0.23 0.32 0.10 南北走向裂缝 砂岩组 0.09 0.32 0.1 0.27 0.22 泥岩组 0.13 0.20 0.26 0.32 0.09

下载CSV 表 4 塔里木盆地迪那2气田融合属性体相关性分析权重系数统计表 Table 4 Weight coefficient statistics of correlation analysis of fusion attribute volume in Dina-2 gas field, Tarim Basin

属性体融合计算公式为

式中：D_S为融合属性体；F_i为不同属性体权重系数；P_i(s)属性体值；P_i为属性体平均值；σ_Pi为属性体标准差。

将计算完成的融合体值采样到单井上，再次与单井成像解释的裂缝密度曲线做线性判别分析，得到融合体与单井裂缝的相关系数值r，最后计算裂缝密度属性场D。

式中：D为裂缝密度场；r为融合体与单井裂缝的相关系数；D_si为融合属性体值；D_si为融合属性体平均值；D_f为单井裂缝密度平均值。

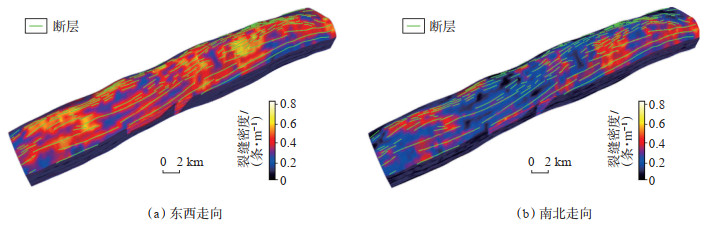
从计算得到的裂缝密度场可以看出，东西走向裂缝主要沿断层分布（图 11a），而南北走向的裂缝主要发育在断层附近，裂缝发育强度明显弱很多（图 11b）。

图 11

Fig. 11

下载原图 图 11 塔里木盆地迪那2气田古近系Su1顶面不同走向裂缝组密度场 Fig. 11 Density field of different fracture groups of Paleogene Su1 top surface in Dina-2 gas field, Tarim Basin

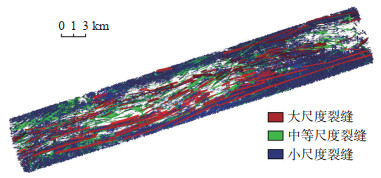
结合以上分析，优选适合的裂缝建模方法，对不同裂缝组设置相应的模型参数（表 5），包括裂缝产状、长度、开度、传导率及空间分布，建立离散裂缝模型，图 12为主力产气层Su1段第1~10层裂缝模拟后的三维空间的分布规律。

表 5(Table 5)

表 5 塔里木盆地迪那2气田离散裂缝建模参数 Table 5 Discrete fracture modeling parameters in Dina-2 gas field, Tarim Basin 裂缝级次 裂缝分组 建模方法 走向/（°） 倾向/（°） 长度/m 开度/mm 传导率/（mD·m） 分形维数 均值 方差 均值 方差 均值 方差 均值 方差 均值 方差 大尺度 区域逆断层 确定性 — — — — — — 0.40 0 680 0 — 中等尺度 正断层带 随机性 70 30 70 15 520 130 0.30 0.10 300 80 1.35 小尺度 东西向 离散性 80 15 70 15 350 70 0.15 0.05 100 25 — 南北向 离散性 2 15 70 15 300 50 1.10 0.03 50 10 —

下载CSV 表 5 塔里木盆地迪那2气田离散裂缝建模参数 Table 5 Discrete fracture modeling parameters in Dina-2 gas field, Tarim Basin

图 12

Fig. 12

下载原图 图 12 塔里木盆地迪那2气田ZOI离散裂缝三维空间分布 Fig. 12 Three-dimensional spatial distribution of ZOI discrete fractures in Dina-2 gas field, Tarim Basin

裂缝孔隙度和渗透率参数会影响数值模型的收敛程度和历史拟合率，而裂缝渗透率作为对流体渗流影响最大的参数，是裂缝研究最关注的属性。利用裂缝建模软件FracaFlow的动态验证功能，通过流量计模拟、试井解释模拟、动态自动校正、指导校正等手段优化已经建好的静态裂缝模型，模拟的Kh（地层系数）值与测量Kh值最大误差小于10%，总体误差小于5%（表 6），说明应用多信息裂缝表征、分级次裂缝建模、动态优化裂缝建模等一系列裂缝研究技术能更好地反映裂缝发育规律。

表 6(Table 6)

表 6 塔里木盆地迪那2气田动态优化后裂缝模型Kh值误差统计 Table 6 Error of Kh values of fracture model after dynamic optimization in Dina-2 gas field, Tarim Basin 井名 测量Kh/（mD·m） 模拟Kh/（mD·m） 绝对误差/（mD·m） 相对误差/% DN201 39.60 41.28 1.68 4.25 DN202 3307.91 3087.93 -219.98 -6.65 DN204 1755.10 1658.39 -96.71 -5.51 DN2-11 7922.77 8423.49 500.72 6.32 DN2-14 607.01 591.47 -15.54 -2.56 DN2-17 12.71 13.05 0.34 2.65 DN22 306.50 314.62 8.12 2.65 DN2-22 1890.22 1720.67 -169.55 -8.97 DN2-27 1216.62 1253.36 36.74 3.02 DN2-28 4381.80 4624.99 243.19 5.55 DN2-B2 312.33 293.22 -19.11 -6.12 DN2-J5 1733.31 1806.11 72.80 4.20

下载CSV 表 6 塔里木盆地迪那2气田动态优化后裂缝模型Kh值误差统计 Table 6 Error of Kh values of fracture model after dynamic optimization in Dina-2 gas field, Tarim Basin

（1）塔里木盆地迪那2气田古近系裂缝走向以近东西向为主，多发育高角度斜交缝和垂直缝，水平缝和低角度斜交缝基本不发育。宏观裂缝真开度普遍小于0.460 mm，线密度均值为0.730条/m，充填程度较高，充填物以泥质、方解石、石膏最为常见；微观裂缝真开度小于0.037 mm，面密度均值为0.031条/m²，充填程度低。裂缝多为与构造变形及断裂作用相关的剪裂缝。

（2）三维最小曲率地震属性对迪那2气田古近系断层和裂缝响应敏感，利用构造光滑、三维边界探测和边界加强联合技术识别的蚂蚁体能清楚地反映其断层或裂缝的分布。

（3）迪那2气田分流河道及河口坝中发育的中细砂岩、粉砂岩中裂缝密度最大，岩层厚度与其平均裂缝线密度呈“座椅式”负相关，断层影响周围裂缝发育的最大距断层距离为300 m左右。

（4）采用相控条件下的序贯高斯随机模拟方法对储层物性进行模拟，模拟前后数据对比显示，孔隙度和渗透率数据基本保持一致；计算模型地质储量较真实储量误差小，地质模型整体上能客观反映迪那2气藏的地质特征。

（5）以动态数据为依据优化静态裂缝模型的一整套预测裂缝分布的技术和方法在迪那2气田是行之有效、且真实可靠的，可为下一步数值模拟提供高质量地质模型。