2. 阿尔伯塔大学 石油工程学院,埃德蒙顿 T6 G1 H9
2. Faculty of Petroleum Engineering, University of Alberta, Edmonton T6 G1 H9, Canada
以往研究与矿场实践表明,SAGD(蒸汽辅助重力泄油)开发过程中,蒸汽腔覆盖层和底界的大量热损失会导致井组油汽比快速下降、效益变差[1-3],因此SAGD不适应于开发连续厚度小于15 m的超稠油。基于此,在SAGD产量预测方面考虑顶底盖层热损失和边界效应变得尤为重要。针对SAGD产油量预测解析理论模型,学者们已做了大量研究,Butler[1]提出了双水平井SAGD的经典泄油理论模型;王大为等[4]、孙新革[5]、秦明[6]等在此基础上进行了进一步研究,使得SAGD产油量预测准确度得到了提高。但由于未考虑在蒸汽腔向顶部、边部和底部推进过程中热扩散速度的非稳态传热特征,现有理论对SAGD顶底盖层热损失、油汽比、热利用率等关键参数的预测精度不够。
在稠油注蒸汽SAGD传热理论计算方面,国内开展的相关研究较少。吴永彬等[7-8]针对SAGD注汽井筒内的关键参数进行了解析求解和预测,并针对SAGD循环预热过程中的井间储层传热与升温解析算法进行了研究。在国外,Butler[9]推导了蒸汽驱的热损失计算理论模型,通过将恒速蒸汽驱蒸汽推进过程简化为全油层柱塞式推进模式,实现了恒速蒸汽驱上覆地层、下伏地层热损失和热效率的计算。但简化的蒸汽推进模式忽略了蒸汽超覆所产生的影响,且对于SAGD来说,蒸汽腔首先上升到油层顶部,然后横向扩展,最后下降,与蒸汽驱存在不同的蒸汽腔运移模式和开发阶段,因此蒸汽驱的热损失计算模型并不能直接用于SAGD开发过程的计算。
目前,针对SAGD顶底盖层热损失影响的计算主要依赖数值模拟软件。如Siavashi等[10]、Sivaram-krishnan等[11]、于天忠等[12]利用CMG-STARS数值模拟软件对SAGD的温度场分布、蒸汽腔扩展、油汽比、蒸汽热利用率等进行了研究。但数值模拟软件计算时涉及的因素复杂,运算时间长,无法满足油田矿场生产的快捷计算及应用的要求。
基于非稳态传热的SAGD开发关键指标的解析方法,需要首先明确顶底盖层与边界效应综合影响下的非稳态传热问题[13-14]。为此,从传热学角度出发,综合油藏工程、工程热物理等多学科理论,推导包含地质参数、热力学参数、流体参数及开发参数中的油汽比、蒸汽热利用率等指标的解析解,并以新疆风城油田重32井区齐古组油藏SAGD井组为例,开展模型的验证与应用。
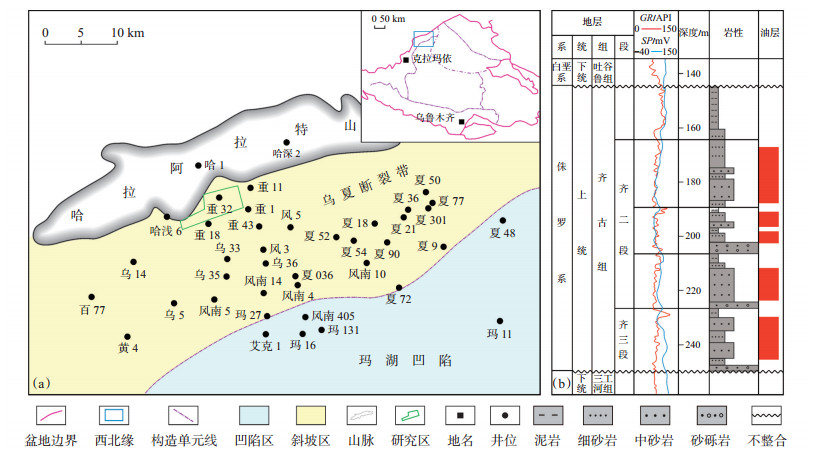
1 地质概况准噶尔盆地风城油田重32井区SAGD开发区油藏位于准噶尔盆地西北缘乌夏断裂带乌尔禾断鼻构造带[15],北以哈拉阿拉特山为界,南邻玛湖凹陷北部斜坡带(图 1a)。重32井区地层发育齐全,自下而上发育石炭系(C)、二叠系(P)、三叠系(T)、侏罗系三工河组(J1s)、齐古组(J3q)、白垩系吐谷鲁组(K1tg)等[16-17]。齐古组为SAGD开发的目的层,不整合覆盖于三工河组之上,整体为南倾的单斜构造,发育泥岩、细砂岩、中—细砂岩、砂砾岩,属辫状河沉积,发育河道、心滩、泛滥平原等沉积微相,储层岩性以中—细砂岩为主(图 1b)。SAGD井组位于齐二段(J3q2)、齐三段(J3q3),油层有效厚度为11~25 m,平均孔隙度为31.2%,平均渗透率为1 870 mD,原始含油饱和度为70.3%。油藏原始地层温度为19.6 ℃,原始地层压力系数为0.987,50 ℃原油黏度为8 000~28 000 mPa·s,黏温反应敏感,温度每升高10 ℃原油黏度降低50%~70%。研究区目前有31对SAGD井组,均处于蒸汽腔扩展或下压生产阶段。
|
下载原图 图 1 准噶尔盆地风城油田重32井区油藏位置(a)及岩性地层综合柱状图(b) Fig. 1 Reservoir location(a)and stratigraphic column(b)of Zhong 32 well area in Fengcheng oilfield, Junggar Basin |
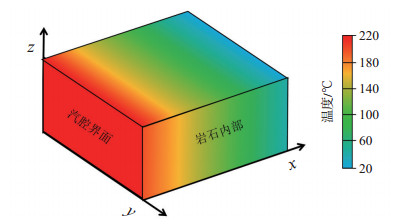
基于SAGD开发模式及蒸汽腔在地层中的传热特征,设定假设条件:①油层等厚且均质;②蒸汽腔扩展稳定;③地层热扩散以热传导为主;④SAGD井组规则分布;⑤忽略沿水平段两端的热传导。建立坐标体系:以蒸汽腔前缘界面建立坐标系,蒸汽腔界面指向岩石内部的法线方向为x,蒸汽腔界面走向线方向为y,沿蒸汽腔界面倾斜线方向为z(图 2)。
|
下载原图 图 2 蒸汽腔前缘界面坐标系示意 Fig. 2 Coordinate system diagram of steam chamber front interface |
以往学者们已推导了毕渥数(Bi)大于1的无限大地层的一维非稳态传热解析解,如Carslaw等[18]、杨世铭等[19]求得解析解为
| $ t(x, \tau ) = {t_{\rm{s}}} - 2\frac{{{t_{\rm{s}}} - {t_{\rm{R}}}}}{{\sqrt {\rm{ \mathsf{ π} }} }}\int_0^{\frac{x}{{2\sqrt {\alpha \tau } }}} {{{\rm{e}}^{ - {\xi ^2}}}} {\rm{d}}\xi \;\;\;x \ge 0 $ | (1) |
式中:t为温度,℃;x为传热距离,m;τ为时间,s;ts为蒸汽腔温度,℃;tR为原始地层温度,℃;α为热扩散率,m2/s。式(1)的局限性主要在于模型外边界不一致,Carslaw等[18]认为升温幅度小于1% 即近似等于原始温度时,热量传播深度为
| $ \frac{\partial^2 t}{\partial x^2}+\frac{\partial^2 t}{\partial y^2}+\frac{\partial^2 t}{\partial z^2}=\frac{1}{\alpha} \frac{\partial t}{\partial \tau} $ | (2) |
式中:x,y,z为3个方向的传热距离,m;当
| $ t(x, \tau)=C_0-C_1 \int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi $ | (3) |
式中:C0,C1均为一元二阶微分方程积分产生的系数。因蒸汽接触地层岩石后,发生相变,释放大量相变热焓,所以在蒸汽腔界面的蒸汽一侧可认为热阻为0,而蒸汽腔界面地层一侧以热传导为主并辅以少量热对流,且存在一定热阻,满足Bi > 1,则内边界条件为x = 0时,t = ts,相当于ξ =
| $ t(x, \tau)=t_{\mathrm{s}}-C_1 \int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi $ | (4) |
因积分部分为单调函数,引入变量C2,且满足
| $ C_2=\frac{x_1}{\sqrt{\alpha \tau_1}}=\frac{x_2}{\sqrt{\alpha \tau_2}} $ | (5) |
即温度场传播深度可表示为
| $ x=C_2 \sqrt{\alpha \tau} $ | (6) |
设原始地层温度为t,则外边界条件可表示为
| $ \left.t(x, \tau)\right|_{x=C_2 \sqrt{\alpha \tau}}=t_{\mathrm{R}} $ | (7) |
将式(7)的外边界条件,代入式(4),解得C1
| $ C_1=\frac{t_{\mathrm{s}}-t_{\mathrm{R}}}{\int_0^{C_2 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} $ | (8) |
将式(8)代入式(4),得到一维非稳态热传导温度场
| $ \begin{cases}t_{\mathrm{s}}-\frac{t_{\mathrm{s}}-t_{\mathrm{R}}}{\int_0^{C_2 \sqrt{a}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi, & 0 \leqslant x \leqslant C_2 \sqrt{\alpha \tau} \\ t_{\mathrm{R}} & x>C_2 \sqrt{\alpha \tau}\end{cases} $ | (9) |
式中:C2为计算过程中产生的系数。
与以往的非稳态传热温度场解析解进行对比表明,本次研究设定的温度传播深度为x = C2
| $ \frac{\partial t}{\partial x}(x, \tau)=-\frac{t_{\mathrm{s}}-t_{\mathrm{R}}}{\sqrt{\tau} \int_0^{C_2 \sqrt{a}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \mathrm{e}^{-\frac{x^2}{4 \alpha \tau}} $ | (10) |
在传热界面处(即x = 0),根据傅里叶定律,对时间域[0,τ]区间积分,得到单位面积蒸汽腔界面累积吸热与时间的关系为
| $ \psi=\frac{2 \lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{\int_0^{c_2 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \sqrt{\tau} $ | (11) |
式中:ψ为单位面积累积吸热量,J/m2;λ为导热系数,J/(m·d·℃)。根据式(9),在空间域[0,C2
| $ \psi^{\prime}=\int_0^{C_2 \sqrt{\alpha}}\left(t_{\mathrm{s}}-t_{\mathrm{R}}-\frac{t_{\mathrm{s}}-t_{\mathrm{R}}}{\int_0^{C_2 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi\right) C \rho \mathrm{d} x $ | (12) |
式中:ψ' 为单位面积累积存储热量,J/m2;C为地层比热容,J/(kg·℃);ρ为地层密度,kg/m3;根据能量守恒原理,式(11)与式(12)相等,化简得到
| $ 2 \alpha \sqrt{\tau}=\int_0^{c_2 \sqrt{\alpha \tau}}\left(\int_0^{c_2 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi-\int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi\right) \mathrm{d} x $ | (13) |
根据地层不同的热扩散率α,通过求解式(13),即可得到C2的值。以风城超稠油储层及下伏地层热扩散率均等于7.287×10-7 m2/s,上覆地层热扩散率等于4.828×10-7 m2 /s为例,在不同加热时间,C2取值如表 1所列。与以往的传热解析公式不同,本次研究中的取值不是一个定值。
|
|
下载CSV 表 1 准噶尔盆地风城油田重32井区SAGD上覆地层传热时间与系数C2取值关系 Table 1 Relationship of heat transfer time and calculated C2 value for SAGD overlying layers of Zhong 32 well area in Fengcheng oilfield, Junggar Basin |
不同油层厚度和泄油范围的SAGD开发时间不同,平均需要7~15 a,取值为5.4~5.6。将的值代入式(9),得到适用于SAGD开发的非稳态热传导储层温度场解析公式
| $ t(x, \tau) \begin{cases}t_s-\frac{t_{\mathrm{s}}-t_{\mathrm{R}}}{\int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \int_0^{\frac{x}{\sqrt{\tau}}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi, & 0 \leqslant x \leqslant 5.5 \sqrt{\alpha \tau} \\ t_{\mathrm{R}} & x>5.5 \sqrt{\alpha \tau}\end{cases} $ | (14) |
结合式(11),可建立传热深度与单位面积累积传热量的关系式
| $ \psi=\frac{2 \lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{\int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \frac{x}{5.5 \sqrt{\alpha}} $ | (15) |
因Butler考虑边界产量模型计算准确度较高[6],所以采用Butler考虑边界产量模型[20],蒸汽腔上升阶段产量计算公式为
| $ q_{\mathrm{o}}=5.32 L\left(\frac{k g \alpha_{\mathrm{o}} \rho_{\mathrm{o}}}{m \mu_{\mathrm{so}}}\right)^{\frac{2}{3}}\left(\varphi \Delta s_{\mathrm{o}} \tau\right)^{\frac{1}{3}} $ | (16) |
蒸汽腔横向扩展阶段产量计算公式为
| $ q_{\mathrm{o}}=L\left(\sqrt{\frac{6 k g \alpha_0 \varphi \Delta s_{\mathrm{o}} h \rho_{\mathrm{o}}}{m \mu_{\mathrm{so}}}}-\frac{\operatorname{kg} \alpha_{\mathrm{o}} \rho_{\mathrm{o}} \tau^2}{m \mu_{\mathrm{so}} A^2} \sqrt{\frac{8 k g \alpha_{\mathrm{o}} \rho_{\mathrm{o}}}{3 \varphi \Delta s_{\mathrm{o}} h m \mu_{\mathrm{so}}}}\right) $ | (17) |
式中:qo为每秒产油量,m3;L为水平段长度,m;k为油层垂向渗透率,mD;αo为油层热扩散率,m2 /s;φ为油层孔隙度,%;ρo为原油密度,kg/m3;Δso为汽腔内部含油饱和度下降量,%;h为油层厚度,m;μso蒸汽腔温度条件下的原油黏度,mPa·s;A为水平井到井组边界距离,m;g为重力加速度,m/s2;m为经验常数,一般为3~5。
3.2 产水量计算模型SAGD产水量主要源于加热油层冷凝水、上覆地层冷凝水、下伏地层冷凝水、一定干度蒸汽的自带液相等的量之和。
(1)加热油层蒸汽冷凝水量qw1
产出的原油体积由蒸汽腔占据,可得出加热油层蒸汽冷凝水量与产量的关系
| $ {{q}_{\text{w}1}}=\rho {{C}_{\text{o}}}\left( {{t}_{\text{s}}}-{{t}_{\text{R}}} \right)\frac{{{q}_{\text{o}}}}{\Delta {{s}_{\text{o}}}\varphi H{}^\backprime{}} $ | (18) |
式中:qw1为每秒蒸汽自带液相组分,m3;H` 为水蒸汽相变热焓,J/t;ρ为油层含流体岩石密度,kg/m3;Co为油层含流体岩石比热容,J/(kg·℃)。
(2)上覆地层散热形成蒸汽冷凝水量qw2
| $ q_{\mathrm{w} 2}=\frac{4 \lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right) L A}{H {{}^\backprime{}}\tau_2 \int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \sqrt{\tau} $ | (19) |
式中:qw2为上覆地层散热每秒形成蒸汽冷凝水量,m3;τ2为蒸汽腔扩展到边的时间,s。
(3)下伏地层散热形成的蒸汽冷凝水量qw3
在蒸汽腔下伏地层,热量同样以非稳态形式向下传导。与上覆地层不同的是,下伏地层温度场不断向下传播的同时,蒸汽腔界面也在向下移动,且满足蒸汽腔界面温度始终为ts,温度场外边界温度始终为tR,即通过刻画下伏地层剖面温度场传播深度,可计算出下伏地层每个微元面下方存储的热量。在τi时刻,横向距离为
| $ \max \left[x\left(\tau_i\right)\right]=5.5 \sqrt{\alpha\left(\tau-\tau_i\right)}-\left[1-\frac{N(\tau)}{N\left(\tau_i\right)}\right] h $ | (20) |
式中:N (τ) 为时刻的累积产油量,m3;N (τi) 为时刻的累积产油量,m3;max[x (τi)] 为τi时刻蒸汽腔横向扩展的位置在τ时刻的最大传热深度,m。
根据式(15)得到的任意τ时刻下伏地层的累积存热量,再除以蒸汽相变热焓,得到任意τ时刻下伏地层的累积产水量
| $ \int_0^\tau q_{\mathrm{w} 3} \mathrm{~d} \tau=\int_0^\tau \frac{2 L \lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{H^{\prime} \int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \frac{\max \left[x\left(\tau_i\right)\right]}{5.5 \sqrt{\alpha}} \frac{q_{\mathrm{o}}\left(\tau_i\right)}{\Delta s_{\rm{o}} \varphi h L} \mathrm{~d} \tau_i $ | (21) |
式中:qw3为下伏地层散热每秒形成的蒸汽冷凝水量,m3。对式(21)的时间求导,得到下伏地层产水量qw3,因该部分计算较为复杂,可以借助计算机编程实现。
(4)总产水量qw
蒸汽自带液相组分qw4只与蒸汽干度X相关,通过换算,得到总产水量
| $ q_{\mathrm{w}}=q_{\mathrm{w} 1}+q_{\mathrm{w} 2}+q_{\mathrm{w} 3}+q_{\mathrm{w} 4}=\frac{q_{\mathrm{w} 1}+q_{\mathrm{w} 2}+q_{\mathrm{w} 3}}{X} $ | (22) |
式中:qw4为每秒蒸汽自带液相组分,m3;qw为每秒总产水量,m3;X为蒸汽干度,是气相质量与湿蒸汽总质量的比值。
3.3 蒸汽热利用率与油汽比计算模型根据式(16)、式(17),可以求出蒸汽腔扩展至边界的时间为τ2,对产水量在时间[0,τ2] 区间积分,得到蒸汽腔横向扩展阶段累积产水量
| $ \begin{aligned} q_{\mathrm{w} \text { 横向 }}= & \frac{L\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{H {{}^\backprime{}}X}\left[\rho C_{\mathrm{o}} h A+\frac{8 \lambda A}{3 \int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \sqrt{\tau_2}+\right. \\ & \left.\int_0^{\tau_2} \frac{2 \lambda}{\int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \frac{\max \left[x\left(\tau_i\right)\right]}{5.5 \sqrt{\alpha}} \frac{q_{\mathrm{o}}\left(\tau_i\right)}{\Delta s_{\mathrm{o}} \varphi h L} \mathrm{~d} \tau_i\right] \end{aligned} $ | (23) |
式中:qw横向为蒸汽腔横向扩展阶段累积产水量,m3。则蒸汽腔上升及横向扩展阶段的蒸汽热利用率(加热油层热量与消耗蒸汽总热量的比值)为
| $ {{\eta }_{\text{横向}}}=\frac{\rho {{C}_{{\rm{o}}}}h}{\rho {{C}_{\text{o}}}h+\frac{8\lambda }{3\int_{0}^{5.5\sqrt{\alpha }}{{{\text{e}}^{-\frac{{{\xi }^{2}}}{4\alpha }}}}\text{d}\xi }\sqrt{{{\tau }^{2}}}+\int_{0}^{{{\tau }_{2}}}{\frac{2L\lambda }{\int_{0}^{5.5\sqrt{\alpha }}{{{\text{e}}^{-\frac{{{\xi }^{2}}}{4\alpha }}}}\text{d}\xi }}\frac{\max \left[ x\left( {{\tau }_{i}} \right) \right]}{5.5\sqrt{\alpha }}\frac{{{q}_{\text{o}}}\left( {{\tau }_{i}} \right)}{\Delta {{s}_{{\rm{o}}}}\varphi hL}~\text{d}{{\tau }_{i}}} $ | (24) |
式中:η横向为蒸汽腔横向扩展阶段蒸汽热利用率。SAGD蒸汽腔上升及横向扩展阶段,累积体积油汽比为
| $ R_{\mathrm{os} \text { 横向 }}=\frac{H {{}^\backprime{}}X \int_0^{\tau_2} q_{\mathrm{o}} \mathrm{d} \tau}{\frac{\int_0^{\tau_2} q_{\mathrm{o}} \mathrm{d} \tau}{\Delta s_{\rm{o}} \varphi} C_{\mathrm{o}} \rho\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)+\int_0^{\tau_2} q_{\mathrm{w} 2} \mathrm{~d} \tau+\int_0^{\tau_2} q_{\mathrm{w} 3} \mathrm{~d} \tau} $ | (25) |
式中:Ros横向为蒸汽腔下压阶段累积体积油汽比。
4 蒸汽腔下压阶段生产指标解析模型 4.1 产油量计算模型当生产时间大于τ2时,蒸汽腔下压,产量下降,产量计算仍然采用Butler(考虑边界)模型。
4.2 产水量计算模型(1)上覆地层热损失产生的蒸汽冷凝水量qw2
| $ q_{\mathrm{w} 2}=\frac{4 A L}{H{{}^\backprime{}} \tau_2} \frac{\lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{\int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi}\left(\sqrt{\tau}-\sqrt{\tau-\tau_2}\right) $ | (26) |
(2)下伏地层热损失产生的蒸汽冷凝水量qw3
| $ \int_0^\tau q_{\mathrm{w} 3} \mathrm{~d} \tau=\int_0^{\tau_2} \frac{2 L \lambda\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{H ^\backprime{}\int_0^{5.5 \sqrt{\alpha}} \mathrm{e}^{-\frac{\xi^2}{4 \alpha}} \mathrm{d} \xi} \frac{\max \left[x\left(\tau_i\right)\right]}{5.5 \sqrt{\alpha}} \frac{q_{\mathrm{o}}\left(\tau_i\right)}{\Delta s_{\mathrm{o}} \varphi h L} \mathrm{~d} \tau_i $ | (27) |
对式(27)的时间求导,可以得到下伏地层产水量变化qw3,同样这部分也需要借助计算机编程实现,总产水量计算方法同式(22)。
4.3 蒸汽热利用率与油汽比计算模型根据上文公式可得下压阶段的蒸汽热利用率为
| $ \eta_{\text {下压 }}=\frac{\frac{\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{o}} \mathrm{d} \tau}{\Delta s_{\rm{o}} \varphi} C_{\mathrm{o}} \rho\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)}{\frac{\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{o}} \mathrm{d} \tau}{\Delta s_{\mathrm{o}} \varphi} C_{\mathrm{o}} \rho\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)+\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{w} 2} \mathrm{~d} \tau+\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{w} 3} \mathrm{~d} \tau} $ | (28) |
式中:η下压为蒸汽腔下压阶段蒸汽热利用率;τc为达到废弃产量的时间,s。换算得到下压阶段的油汽比为
| $ R_{\mathrm{os} \text { 下压 }}=\frac{H {{}^\backprime{}}X \int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{o}} \mathrm{d} \tau}{\frac{\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{o}} \mathrm{d} \tau}{\Delta s_{\mathrm{o}} \varphi} C_{\mathrm{o}} \rho\left(t_{\mathrm{s}}-t_{\mathrm{R}}\right)+\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{w} 2} \mathrm{~d} \tau+\int_{\tau_2}^{\tau_{\mathrm{c}}} q_{\mathrm{w} 3} \mathrm{~d} \tau} $ | (29) |
式中:Ros下压为蒸汽腔下压阶段累积体积油汽比。
5 编程与实例应用 5.1 程序设计使用Visual Studio程序编程,实现了23种可变参数的输入,以及产油量、累积产油量、油层产水量、上覆地层产水量、下伏地层产水量、蒸汽自带液相水量、总产水量、含水率、体积油汽比、累积体积油汽比、累积采出程度以及下伏地层传热深度剖面共12项结果的输出。
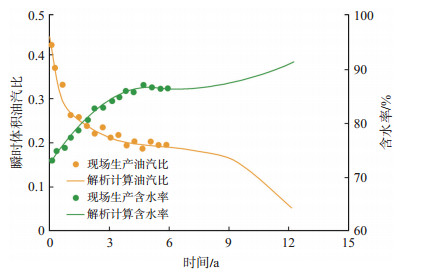
5.2 模型验证利用准噶尔盆地风城油田重32井区典型SAGD井组A进行验证,该井组注汽井上方油层有效厚度为11 m,于2015年10月进入SAGD生产阶段。将井组储层参数计算的瞬时油汽比、含水率曲线(图 3)与现场实际的瞬时油汽比、含水率数据对比可见,本模型的计算结果整体符合率大于95%;产油与产水的现场符合率均大于90%,表明模型计算精度可靠,可用于现场快速计算。
|
下载原图 图 3 准噶尔盆地风城油田重32井区SAGD井组A实测油汽比、含水率与解析计算结果对比 Fig. 3 Comparison betwen measured and analytical oil-steam ratio and water cut values of SAGD well group A of Zhong 32 well area in Fengcheng oilfield, Junggar Basin |
利用本文解析软件,对准噶尔盆地风城油田重32井区油藏SAGD开发区进行快速计算,油藏相关参数如表 2所列。
|
|
下载CSV 表 2 准噶尔盆地风城油田重32井区SAGD开发区油藏相关参数 Table 2 Reservoir parameters of SAGD deployment area of Zhong 32 well area in Fengcheng oilfield, Junggar Basin |
将以上参数输入该程序,设置废弃产量为5 m3/d,得到不同厚度油层下井组全生命周期上覆地层、下伏地层、油层热损失和累积蒸汽热利用率等关系曲线。
(1)不同厚度油层盖层热损失
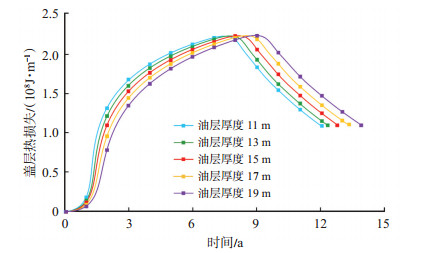
油层厚度越大,盖层热损失越小,热损失速率的上升时间越晚,表明厚度越大,蒸汽腔抬升并达到油层顶部的时间越长;同时,油层厚度越大,油层内的蓄热效应越明显,盖层的热损失相对量越小(图 4)。
|
下载原图 图 4 不同油层厚度的SAGD井组单位水平段长度的盖层热损失曲线 Fig. 4 Overburden heat loss curves per unit SAGD horizontal length under different net pay thickness |
(2)不同厚度油层的下伏地层热损失
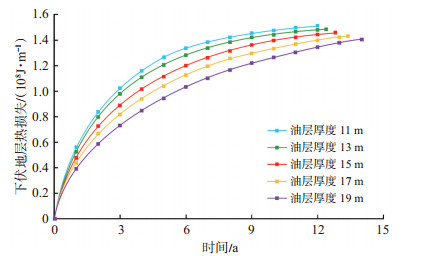
随着SAGD蒸汽腔热场的建立和不断拓展,下伏地层热损失也逐渐增大,当蒸汽腔横向扩展并逐渐下降时,油层厚度越大,下伏地层的热损失量越小,表明更多的蒸汽用于加热油层(图 5)。同时,与盖层热损失曲线相比,存在明显的区别,即下伏地层初期热损失上升较快,而盖层的热损失则经历了一段低值期,原因在于生产井位于油层底部,注汽井距离生产井仅5 m,因此初期的蒸汽腔热场对基底及下伏地层的热影响程度更大,随着蒸汽腔向上抬升,盖层的热损失逐渐大于底部。
|
下载原图 图 5 不同油层厚度的SAGD井组下伏地层热损失曲线 Fig. 5 Underburden heat loss curves per unit SAGD horizontal length under different net pay thickness |
(3)不同厚度油层的蒸汽热利用率(瞬时)
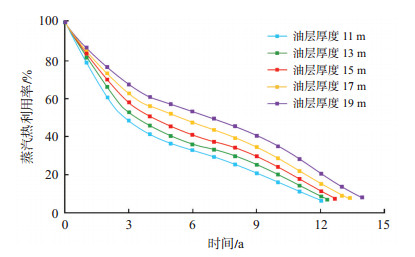
随着蒸汽前缘不断向顶底盖层推进,蒸汽向顶底盖层的热损失逐渐变大,注蒸汽SAGD越往后,蒸汽的热利用率越低。从瞬时热利用率曲线可见(图 6),在注蒸汽开发末期,热利用率下降到10% 以下,即注入蒸汽的热焓速率仅略大于向顶底盖层的热损失速率。且油层越薄,相同时刻蒸汽的热利用率越低,表明薄层注蒸汽向顶底盖层的热损失相对比例越大。
|
下载原图 图 6 不同油层厚度的SAGD井组蒸汽瞬时热利用率曲线 Fig. 6 Steam heat utilization ratio curves of SAGD well group under different net pay thickness |
(4)不同厚度油层的累积油汽比
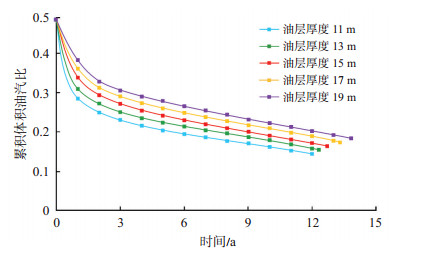
在SAGD注蒸汽早期,蒸汽腔主要处于上升阶段,顶底盖层的热损失并不明显,不同油层厚度的注蒸汽油汽比均超过0.4,即50 m3蒸汽能够采出20 m3以上原油,随着生产时间延长,薄层油汽比迅速下降,油层厚度11 m时对应最终油汽比仅为0.145,而厚度为19 m的油层油汽比能达到0.185,差异明显(图 7)。油汽比的差异主要原因在于蒸汽热利用率的差异,厚层蒸汽的热利用率高,更多的蒸汽用于加热和驱动原油,因此产量和油汽比也更高。
|
下载原图 图 7 不同油层厚度的SAGD井组累积油汽比曲线 Fig. 7 Cumulative oil-steam ratio curves of SAGD well group under different net pay thickness |
(5)不同厚度油层SAGD综合开发指标预测
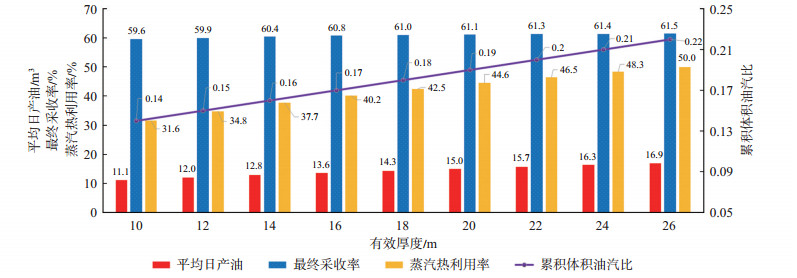
根据本文推导的SAGD关键开发指标参数计算模型,设定有效厚度为10~26 m,废弃产量为5 m3/d时,计算得到油层在不同有效厚度条件下的SAGD综合开发指标数据(图 8)。可以看出,在均质油藏条件下,尽管油层厚度对到达废弃产量时的最终采收率影响较小,但对平均产量、蒸汽热利用率、累积油汽比的影响较大。厚度从10 m提高到26 m,平均日产油从11.1 t提高到16.9 t,油汽比从0.14提高到0.22,蒸汽热利用率从31.6% 提高到50.0%。根据加拿大SAGD开发实践[21],SAGD开发技术经济效益对于蒸汽热利用率的下限为35%,对应到风城油藏条件下的有效厚度应大于12 m。
|
下载原图 图 8 不同厚度的SAGD井组综合开发指标预测 Fig. 8 Systematic SAGD production performance parameters prediction under different net pay thickness |
(1)在上覆与下伏地层非稳态热传导解析解基础上建立SAGD蒸汽腔上升及横向扩展阶段以及蒸汽腔下压阶段的油层蒸汽冷凝水量、上覆地层散热形成蒸汽冷凝水量、下伏地层散热形成的蒸汽冷凝水量解析解,并结合Butler产油量解析公式,推导建立了基于非稳态传热的产水量、蒸汽热利用率、油汽比等关键开发指标计算模型。
(2)克服了以往的非稳态传热解析求解难题,将共计23种地质参数、流体参数、热力学参数、开发参数集成输入,实现了对蒸汽热利用率、上覆地层热损失、下伏地层热损失、油汽比、采收率、日产油等关键指标参数的快速解析求解。此外,还实现了对饱和度、地层温度、油层导热系数、地层导热系数、水平段长度、水平井排距、蒸汽干度等19种参数的联合分析。
(3)利用准噶尔盆地风城油田重32井区典型SAGD井组A,进行了生产油汽比的实测与解析计算结果对比,生产6.4 a符合率达到95% 以上,表明本文解析算法精度较高,可用于生产预测。
(4)准噶尔盆地风城油田重32井区SAGD开发区不同油层厚度的计算结果表明,SAGD开发过程中,蒸汽腔接触上覆地层后形成非稳态热传导,在蒸汽腔横向扩展阶段上覆地层热损失逐渐增加,在汽腔下压阶段热损失逐渐减少;下伏地层具有随汽腔形态和位置变化而变化的非稳态热传导特征,下伏地层热损失在蒸汽腔扩展阶段随下伏地层与蒸汽腔的接触面积增加而持续增加。薄层油藏顶底盖层的热损失大,热利用率大于35% 的油层有效厚度应大于12 m。
| [1] |
BUTLER R M. A new approach to the modelling of steam-assisted gravity drainage. Journal of Canadian Petroleum Technology, 1985, 24(3): 42-51. DOI:10.2118/85-03-01 |
| [2] |
BULTER R M. Steam-assisted gravity drainage: Concept, development, performance and future. Journal of Canadian Petroleum Technology, 1994, 33(2): 44-50. DOI:10.2118/94-02-05 |
| [3] |
周明升. 超稠油蒸汽辅助重力泄油开发技术应用研究[D]. 大庆: 东北石油大学, 2010: 30-38. ZHOU Mingsheng. Study on the application of steam assisted gravity drainage technology in the development of super heavy oil[D]. Daqing: Northeast Petroleum University, 2010: 30-38. |
| [4] |
王大为, 刘小鸿, 张风义, 等. 各向异性稠油油藏SAGD产能公式校正. 岩性油气藏, 2014, 26(1): 123-126. WANG Dawei, LIU Xiaohong, ZHANG Fengyi, et al. Correction of SAGD productivity formula in anisotropic heavy oil reservoir. Lithologic Reservoirs, 2014, 26(1): 123-126. DOI:10.3969/j.issn.1673-8926.2014.01.021 |
| [5] |
孙新革. 浅层超稠油双水平井SAGD技术油藏工程优化研究与应用[D]. 南充: 西南石油大学, 2012: 4-127. SUN Xinge. Reservoir engineering optimization research and application of SAGD technology in shallow super heavy oil dual horizontal wells[D]. Nanchong: Southwest Petroleum University, 2012: 4-127. |
| [6] |
秦明. 蒸汽辅助重力泄油产量预测模型研究[D]. 成都: 西南石油大学, 2016: 14-21. QIN Ming. Study on the production prediction model of steam assisted gravity drainage[D]. Chengdu: Southwest Petroleum University, 2016: 14-21. |
| [7] |
吴永彬, 李秀峦, 孙新革, 等. 双水平井蒸汽辅助重力泄油注汽井筒关键参数预测模型. 石油勘探与开发, 2012, 39(4): 481-488. WU Yongbin, LI Xiuluan, SUN Xinge, et al. Key parameters forecast model for injector wellbores during the dual-well SAGD process. Petroleum Exploration and Development, 2012, 39(4): 481-488. |
| [8] |
吴永彬, 李秀峦, 赵睿, 等. 双水平井SAGD循环预热连通判断新解析模型. 西南石油大学学报(自然科学版), 2016, 38(1): 84-91. WU Yongbin, LI Xiuluan, ZHAO Rui, et al. A new analytical model of heat communication judgement during heat circulation phase of dual-horizontal SAGD. Journal of Southwest Petroleum University(Science & Technology Edition), 2016, 38(1): 84-91. |
| [9] |
BUTLER R M. 重油和沥青的热力开采工艺[M]. 王秉璋, 译. 北京: 石油工业出版社, 1994: 54-65. Butler R M. Thermal recovery of oil and bitumen[M]. WANG Bingzhang, trans. Beijing: Petroleum Industry Press, 1994: 54-65. |
| [10] |
SIAVASHI M, GARUSI H, DERAKHSHAN S. Numerical simulation and optimization of steam-assisted gravity drainage with temperature, rate, and well distance control using an efficient hybrid optimization technique. Numerical Heat Transfer Applications, 2017, 72(9): 1-24. |
| [11] |
SIVARAMKRISHNAN K, HUANG B, JANA A K. Predicting wellbore dynamics in a steam-assisted gravity drainage system: Numeric and semi-analytic model, and validation. Applied Thermal Engineering, 2015, 91: 679-686. DOI:10.1016/j.applthermaleng.2015.08.041 |
| [12] |
于天忠, 张建国, 叶双江, 等. 辽河油田曙一区杜84块超稠油油藏水平井热采开发技术研究. 岩性油气藏, 2011, 23(6): 114-119. YU Tianzhong, ZHANG Jianguo, YE Shuangjiang, et al. Development technology with thermal recovery for horizontal well of superheavy oil reservoir in Du 84 block in Shu 1 area, Liaohe Oilfield. Lithologic Reservoirs, 2011, 23(6): 114-119. DOI:10.3969/j.issn.1673-8926.2011.06.027 |
| [13] |
PANG Zhanxi, WU Zhengbin, ZHAO Meng. A novel method to calculate consumption of non-condensate gas during steam assistant gravity drainage in heavy oil reservoirs. Energy, 2017, 130: 76-85. DOI:10.1016/j.energy.2017.04.078 |
| [14] |
田杰, 刘慧卿, 庞占喜, 等. 高压环境双水平井SAGD三维物理模拟实验. 石油学报, 2017, 38(4): 95-102. TIAN Jie, LIU Huiqing, PANG Zhanxi, et al. Experiment of 3D physical simulation on dual horizontal well SAGD under high pressure condition. Acta Petrolei Sinica, 2017, 38(4): 95-102. |
| [15] |
宫博识, 文华国, 李丛林, 等. 准噶尔盆地乌尔禾地区风城组沉积环境分析. 岩性油气藏, 2014, 26(2): 59-66. GONG Boshi, WEN Huaguo, LI Conglin, et al. Sedimentary environment of Fengcheng Formation in Urho area, Junggar Basin. Lithologic Reservoirs, 2014, 26(2): 59-66. |
| [16] |
杨帆, 卞保力, 刘慧颖, 等. 玛湖凹陷二叠系夏子街组限制性湖盆扇三角洲沉积特征. 岩性油气藏, 2022, 34(5): 63-72. YANG Fan, BIAN Baoli, LIU Huiying, et al. Sedimentary characteristics of fan delta in restricted lacustrine basin of Permian Xiazijie Formation in Mahu Sag. Lithologic Reservoirs, 2022, 34(5): 63-72. |
| [17] |
冯有良, 胡素云, 李建忠, 等. 准噶尔盆地西北缘同沉积构造坡折对层序建造和岩性油气藏富集带的控制. 岩性油气藏, 2018, 30(4): 14-25. FENG Youliang, HU Suyun, LI Jianzhong, et al. Controls of syndepotitional structural slope-break zones on sequence architecture and enrichment zones of lithologic reservoirs in northwestern margin of Junggar Basin. Lithologic Reservoirs, 2018, 30(4): 14-25. |
| [18] |
CARSLAW H S, JAEGER J C. Conduction of heat in solids. Oxford: Oxford Science Publications, 1986.
|
| [19] |
杨世铭, 陶文铨. 传热学. 北京: 高等教育出版社, 2006: 133-137. YANG Shiming, TAO Wenquan. Heat transfer. Beijing: Higher Education Press, 2006: 133-137. |
| [20] |
BUTLER R M, MCNAB G S, LO H Y. Theoretical studies on the gravity drainage of heavy oil during in-situ steam heating. The Canadian Journal of Chemical Engineering, 1981, 59: 455-60. |
| [21] |
PINTO H, WANG X, GATES I. On the ratio of energy produced to energy injected in SAGD: Long-term consequences of early stage operational decisions. Journal of Petroleum Science and Engineering, 2021, 199: 108271. |
 2023, Vol. 35
2023, Vol. 35




