2. 中国石油大学 (北京), 北京 昌平 102249;
3. 中国石油大庆油田有限责任公司 采气分公司, 黑龙江 大庆 163000
2. China University of Petroleum(Beijing), Beijing 102249, China;
3. Gas Production Company, PetroChina Daqing Oilfield Company, Daqing 163000, Heilongjiang, China
随着油气资源的开发利用,勘探开发成本低、类型相对简单的构造型油气藏大多已被发现和开发,而复杂构造区往往是一些成藏质量较差的区域,地震成像复杂,勘探难度大,因此高精度地震成像需求越来越迫切。弹性波全波形反演(EFWI)是利用多分量地震记录的多种波场信息进行岩性参数反演,相比其他的建模方法具有更高的精度[1]。以全波形反演为代表的地震反演成像技术在地震地质建模综合研究中也扮演着越来越重要的角色[2],但是EFWI存在很强的非线性,初始模型的建立、低频数据的缺失等问题均可能导致反演陷入局部极小值,从而制约了EFWI在实际资料(尤其是陆上实际资料)中的推广应用。
全波形反演(FWI)需要直接求取目标函数对模型参数的导数从而进行速度更新,这将带来巨大的计算量和存储量。为克服大计算量问题,Lailly[3]提出了基于震源波场和残差波场的梯度求取方法,其具体做法是对2种波场进行一次互相关。该方法对于每个单独激发的震源只要正演2次就可进行1次更新,能够减少全波形反演的计算量,由于该方法是基于线性理论的,对模型的大尺度背景恢复起来很困难。Tarantola[4]基于时间域纵波方程将非线性原理应用到最小二乘反演中,并推导出了利用伴随方程法求取介质参数更新方向的公式。Taranto‐ la[5]基于弹性介质中的波动方程形式提出并实现了利用弹性波进行全波形反演的思路,并将FWI理论推广到了EFWI。任浩然等[6]利用多种地震信息进行建模,但多重因素的叠加加大了反演的非线性并降低了实用性。为降低EFWI的非线性程度,许多学者做了针对性的研究,最常用的是自地震数据低频成分到高频成分逐渐匹配的多尺度反演策略,该策略可以在时间域[7]、频率域[8]和拉普拉斯域[9]实现,但后2种域的计算过程复杂,对计算资源的硬件性能要求更高。在时间域可以通过对地震数据的滤波实现多尺度反演,由于地震数据本身就是时空域的,对地震数据进行时间和空间域相关处理更方便。从小炮检距数据到大炮检距数据的反演,通过限制参与反演数据的炮检距来实现。大炮检距可以有效重建低波数信息,小炮检距则对高波数成分具有很好的恢复作用[10-12]。另外,比较常用的降低EFWI非线性程度的方法是利用初至波进行近地表速度反演,因为EFWI的非线性大部分由反射波引起的,当初始速度精度不够时,反射点很难归位[13],因此,避免反射波参与反演可有效地降低反演的非线性。尽管很多学者针对EFWI的非线性问题进行了大量研究,并在理论模型上得到了验证,但对于实际资料(尤其是陆上资料)而言,EFWI的速度建模方法依然难以见到效果,这是因为陆上资料更容易受震源能量、激发响应、噪音污染、近地表传播方式等的影响[14],从而加剧EFWI的非线性程度。王华忠等[15]指出EFWI的非线性取决于介质模型的复杂性和描述地震波物理传播过程的正算子的复杂性,并在分析了陆上和海上地震数据特点的基础上,提出了全波形反演走向实用化的策略,即利用特征波场反演而不是全波场,同时增加相位信息,尽量充分考虑初始模型的先验信息。
EFWI的非线性很大部分来自于深层反射波,这将直接影响纵、横波速度场的反演精度。为提高速度反演的精度,提出一种分层反演策略:①利用时窗选取包含浅层速度信息的较早时间到达的地震数据,用小偏移距早至波数据,自低频到高频多尺度重建浅层速度场,以减少中深层反射波及噪声带来的强非线性影响,提高浅层速度的反演质量。早至波与初至波一样,并不是特指某一类型的波,而是包含了很多波的信息。小偏移距早至波主要包括浅层直达波、反射波及小折射波等。筛选的具体标准是根据反演浅层界面的深度以及相应深度的初始速度场,估算出地震记录时间,这样选择的偏移距范围内的地震记录时间能够约束地震波穿透深度,从而获得包含浅层速度场的波场记录。在EFWI中,浅层速度的反演精度将直接决定深层反演的好坏。在这个过程中用小尺度交错网格有限差分模拟浅层波场。②固定好浅层速度,用全波场、全偏移距数据对中深层速度进行从低频到高频的多尺度反演,用大尺度交错网格有限差分模拟中深层波场,在减少计算量的同时保证波场模拟的精度。③最后使用伴随波场法求取纵、横波速度梯度,引入深度学习优化器RMSprop[16]的梯度处理方式,提高反演的稳定性和收敛速率,进一步提高深层速度场的反演精度。将该分层反演策略应用到理论模型和陆上实际资料,以期有效提高浅层和中深层速度场的反演精度。
1 方法原理 1.1 时间域EFWI基本原理全波形反演的基本思想是用模拟数据不断地逼近观测获得的实际数据,使它们的误差最小化,此时拟合结果对应的模型参数最接近真实的模型参数。基于模拟和观测记录,全波形反演目标泛函往往可以被定义成多种不同的误差形式,不同形式的目标泛函采用不同的参考标准匹配模拟数据和观测数据。理论上如果目标泛函能够达到一定范围内的极小值,此时的模型参数就会更加接近实际情况。此次研究采用的EFWI目标函数表达式如下:
| $ \chi(m)=\frac{1}{2} \int_0^T \int_{\Omega}\left\|u(m ; x, t)-u^{\mathrm{dbs}}(x, t)\right\|^2 \mathrm{~d} \Omega \mathrm{d} t $ | (1) |
式中:uobs(x, t)为观测记录;u(m; x, t)为正演模拟记录,在分层反演方法中,模拟记录按照分层时窗大小进行调整;dΩ表示对检波点接收区域各道的积分求和;dt表示对记录时间的积分求和;x为地震道;m为模型参数,本文中指浅层及中深层的纵、横波速度;T表示地震记录的时间,s;Ω为检波点接收区域。
直接求取目标函数关于速度的梯度非常困难,比较常用的方法是通过伴随波场求取的伴随方法。Zhang等[17]从Lagrange乘子法原理出发,通过定义褶积型目标函数,得出了基于弹性波波动方程的伴随方程,并给出了相应模型参数的梯度公式,本文采用此种方法求取模型参数的梯度。二维弹性波波动方程通过伴随方程法得到的纵、横波速度场的梯度表达式如下:
| $ \begin{aligned} K_{v_{\mathrm{s}}}= & -2 \rho v_{\mathrm{s}} \int_0^T\left[2\left(\lambda_{x x} \frac{\partial \nu_x}{\partial x}+\lambda_{z z} \frac{\partial \nu_z}{\partial z}\right)+\right. \\ & \left.\lambda_{x z}\left(\frac{\partial \nu_z}{\partial x}+\frac{\partial \nu_x}{\partial z}\right)\right] \mathrm{d} t+4 \rho v_{\mathrm{s}} \int_0^T\left(\lambda_{x x}+\lambda_{z z}\right) \cdot \\ & \left.\left(\frac{\partial \nu_x}{\partial x}+\frac{\partial \nu_z}{\partial z}\right)\right] \mathrm{d} t \end{aligned} $ | (2) |
| $ K_{v_p}=-2 \rho v_{\mathrm{P}} \int_0^T\left(\lambda_{x x}+\lambda_{z z}\right)\left(\frac{\partial \nu_x}{\partial x}+\frac{\partial \nu_z}{\partial z}\right) \mathrm{d} t $ | (3) |
式中:ρ为密度,g/cm3,此次研究不涉及密度反演,因而为常数;vP,vS分别为纵、横波速度,m/s;λ为伴随波场值;v为震源波场值。
1.2 基于RMSProp的共轭梯度优化方法 1.2.1 基本理论EFWI主要利用非线性最优化方法最小化观测记录和理论记录之间的误差,以重建地下介质的物性参数。为了最小化目标函数,通常使用梯度类优化算法来解决非线性问题。牛顿法具有二阶收敛的优势,相较于一阶收敛的最速下降法和介于一阶与二阶收敛的共轭梯度法,它的收敛更快,但是需要直接求取目标函数的海森矩阵,难度较大,且需要巨大的计算量和巨大的内存资源成本,因此该方法在EFWI中很难推广应用。共轭梯度法(CG)的收敛速率介于一阶和二阶方法之间,可求解无约束二次规划问题,由于其表达式简单,实现起来容易,在大规模数据的无约束优化问题中具有独特的优势[18]。其主要逻辑是找到一组共轭正交的方向向量,对每个方向上的模型参数依次进行迭代更新,当每个方向上的误差达到或接近0时,迭代结束。该方法的收敛速度大于最速下降法等一阶的优化方法。它的模型参数更新方式可以用下式表示:
| $ \boldsymbol{d}_n=\left\{\begin{array}{l} -\boldsymbol{g}_n, n=1 \\ -\boldsymbol{g}_n+\frac{\boldsymbol{g}_n^T \boldsymbol{g}_n}{\boldsymbol{g}_{n-1}^T \boldsymbol{g}_{n-1}} \boldsymbol{d}_{n-1}, n \geqslant 2 \end{array}\right. $ | (4) |
式中:gn为公式(2)和(3)所计算的纵波和横波速度的梯度场;n为迭代次数;dn为通过共轭梯度法计算的更新方向,将其代入下式进行模型参数的更新
| $ \boldsymbol{m}_{n+1}=\boldsymbol{m}_n+\alpha \boldsymbol{d}_n $ | (5) |
式中:α为更新步长。RMSProp来源于深度学习,本文将这种优化理论应用到共轭梯度法中,相比于传统共轭梯度方法,新方法可使EFWI收敛更快、反演精度更高。优化后需对纵、横波速度场每个位置的梯度gn做如下处理:
| $ \widetilde{g}_{n, i}=\left\{\begin{array}{l} 0, n=1 \\ \eta \widetilde{g}_{n-1, i}+(1-\eta) g_{n, i}^2, n \geqslant 2 \end{array}\right. $ | (6) |
| $ g_{n, i}^{\mathrm{new}}= \begin{cases}g_{n, i}, & n=1 \\ g_{n, i} \times \frac{1}{\underset{g_{n, i}}{\sim \frac{1}{2}}}, & n \geqslant 2\end{cases} $ | (7) |
式中:gn, i为纵、横波速度梯度gn的第i个元素;
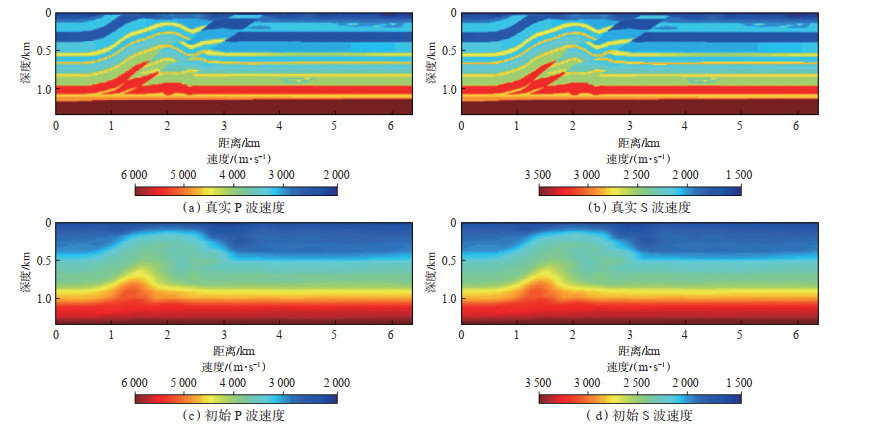
为验证基于RMSProp改进的CG方法对EFWI效果的提升,选择了二维Overthrust模型进行反演测试。在反演参数相同的情况下,分别用传统的CG法和改进后的CG法重建该模型(图 1)。
|
下载原图 图 1 Overthrust模型的真实速度和初始速度 Fig. 1 True and initial velocity of Overthrust model |
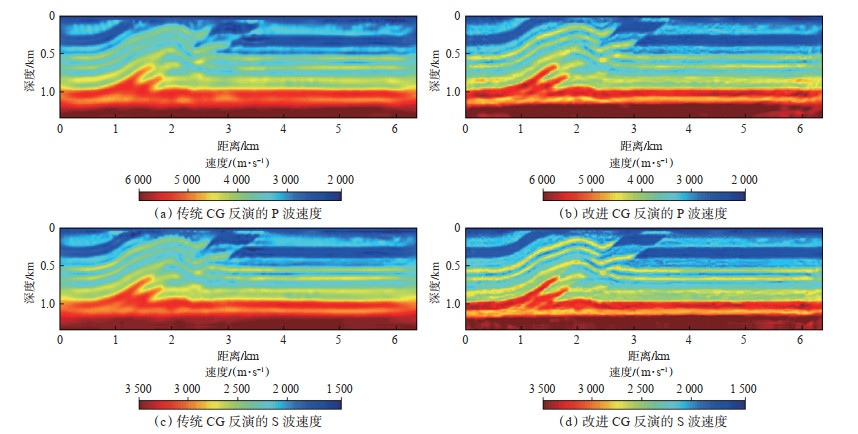
该二维Overthrust模型共计800×170个网格点,交错网格有限差分空间步长为8 m;使用雷克子波生成震源,模型设计50炮,每炮800个检波器;为降低非线性影响,选择多尺度反演,共设置4个频带,各频带的主频依次是4 Hz,7 Hz,11 Hz和15 Hz,每个频带迭代20次。对比2种方法对应的反演结果可以看出,无论是纵波速度还是横波速度,改进后的CG方法重构的速度场精度更高,尤其在深层,构造更加清晰,速度值更接近真实值,说明本文方法能够有效平衡浅层和深层的梯度能量,从而改善深层反演的结果(图 2)。
|
下载原图 图 2 不同方法反演的Overthrust模型速度场对比 Fig. 2 Comparison of velocity field of Overthrust model inversed by different methods |
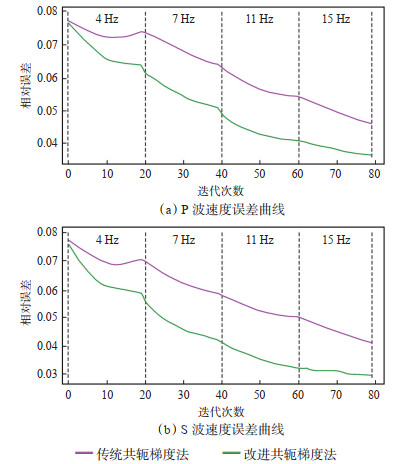
为了更加直观地对比2种方法的反演精度,分别求取了2种方法在整个反演过程中的速度误差值,该误差是基于真实速度模型的相对误差。在4个频带共80次的迭代过程中,改进CG反演的速度误差曲线均位于传统方法误差曲线下方,误差曲线下降更快,说明优化后反演的速度场精度更高,收敛更快,通过更少的迭代次数即可达到传统CG反演的精度(图 3)。
|
下载原图 图 3 不同频带反演速度的相对误差 Fig. 3 Relative errors of inversion velocity in different frequency bands |
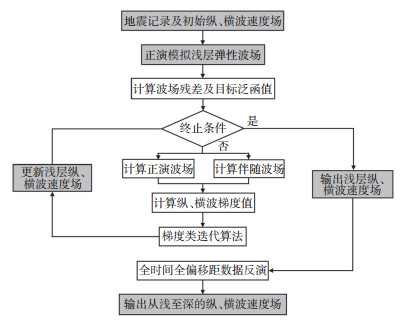
EFWI强非线性是由资料采集等客观因素引起的地震数据与反演参数之间的强不确定性,因此通过筛选不同数据子集,分步骤、多尺度的反演是降低EFWI非线性程度的有效策略(图 4)。基于这一规律的时间域EFWI分层反演策略,可降低反演的非线性程度,提高反演质量。具体反演过程如下:
|
下载原图 图 4 速度场分层反演流程 Fig. 4 Flowsheet of layered inversion of velocity field |
(1)利用反演浅层界面的深度以及相应深度的初始速度,估算出相应地震记录时间,用该时间窗口选取较早到达的地震数据,同时选定偏移距范围。用包含丰富浅层速度信息的小偏移距直达波、小折射波[19]、浅层反射波等早至波反演浅层速度,规避主要由中深层反射波带来的强非线性干扰。
(2)通过从低频到高频逐渐匹配的多尺度反演手段,重建浅层速度。反演时采用小网格剖分的交错网格有限差分方法进行波场模拟,以保证浅层速度波场模拟的精度,提高浅层反演质量。
(3)固定反演重建的浅层速度场,约束中深层反演,降低反演的不确定性,利用全采样时间的全偏移距数据反演中深层速度。
(4)由低频到高频多尺度反演中深层速度,由于中深层速度较大,采用大网格的交错网格有限差分模拟波场,利用含有中深层速度场信息的地震记录段反演中深层速度场。该方法在减少计算量的同时可获得高精度的中深层反演结果。分层反演时速度场梯度需要按照以下公式进行处理
| $ \boldsymbol{g}_n=p(z) \boldsymbol{g}_n $ | (8) |
| $ p(z)=\left\{\begin{array}{l} 0, 0 \leqslant z \leqslant \frac{11 d_1}{12} \\ \mathrm{e}^{-\frac{150}{d_1^2}\left(z-\frac{13}{12} d_1\right)^2}, \frac{11 d_1}{12}<z \leqslant \frac{13 d_1}{12} \\ \frac{12 z}{13 d_1}, \frac{13 d_1}{12}<z \leqslant 2 d_1 \\ \frac{z}{2 d_1}-1+\frac{12 z}{13 d_1}, z>2 d_1 \end{array}\right. $ | (9) |
式中:d1表示浅层速度场的深度,m。梯度gn经过公式(9)定义的分段处理函数p(z) 处理后,浅层梯度值为0,不再更新,而深层梯度的能量得到提升。
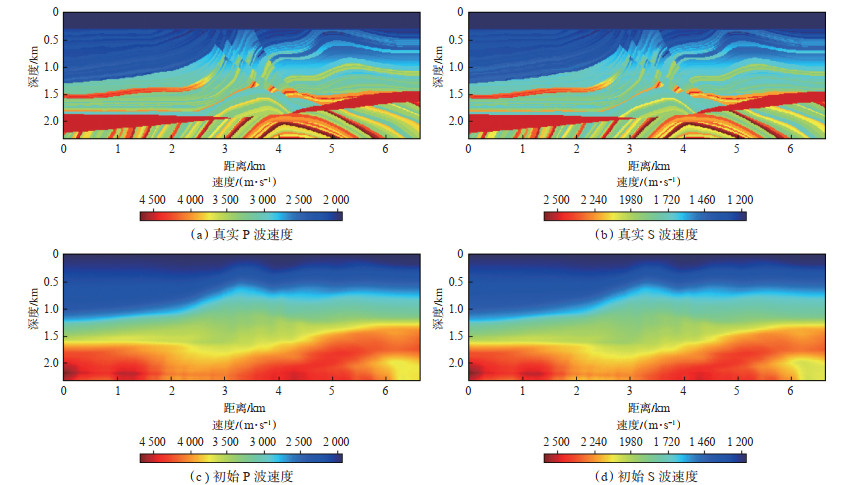
1.3.2 数值算例为验证分层反演策略的有效性,利用二维Mar‐ mousi模型进行测试(图 5)。速度更新时,对二维Marmousi模型的初始速度场分别进行常规EFWI和分层反演策略下的EFWI。整个速度场的地震记录采样时长为4 s,采样间隔为1 ms,共40炮激发,用0~250 ms的时间窗筛选地震记录以确定偏移距范围,进行多尺度反演的雷克子波主频依次为4 Hz,8 Hz,12 Hz,18 Hz和25 Hz。浅层深度为300 m,真实纵、横波速度场深度为0~300 m时为低匀速层,有限差分网格为5 m×5 m。浅层反演结束后固定浅层速度,用整个4 s的全偏移距地震记录进行多频带反演中深层速度场,有限差分网格为10 m×10 m。对比基于2种反演策略得到的纵、横波速度场,可见浅层低匀速层反演结果在反演参数完全相同的情况下,无论是纵波速度还是横波速度,分层反演的低速层均更干净,更接近真实速度场,而常规反演在低匀速层存在干扰;同时,在深度为0~1.5 km,距离为0~6 km的区域内,分层反演得到的纵、横波速度场均更加清晰,局部构造的分辨率更高,弱反射层得到了较好的恢复(图 6)。
|
下载原图 图 5 二维Marmousi模型的真实速度和初始速度 Fig. 5 True and initial velocity of 2D Marmousi model |

|
下载原图 图 6 不同方法的速度反演结果对比 Fig. 6 Comparison of velocity inversion results bydifferent methods |
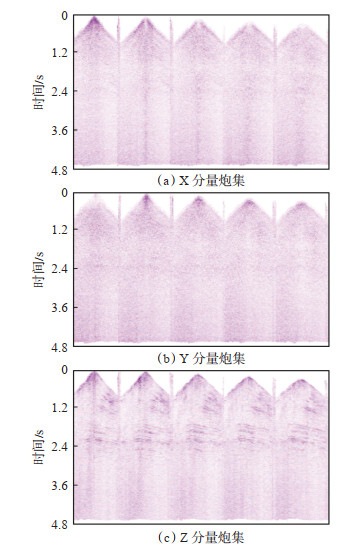
为了进一步测试新方法对实际资料的有效性和适应性,对四川某三维区块的二维测线进行EFWI速度分层建模测试。该三维区块为正交观测系统采集,最小炮检距为28.28 m,覆盖次数为11,道距为40 m,子波主频为25 Hz,三分量地震记录的采样时长为5 s,采样间隔为1 ms。X分量地震记录信噪比低,很难看到有效信息,Y分量信噪比更低,Z分量信噪比相对较高(图 7)。通过层析反演得到该区块的初始速度,待反演的二维速度场横向距离为5 km,纵向深度为7 km。
|
下载原图 图 7 四川某三维区块的三分量地震记录 Fig. 7 Three-component seismic records of a 3D block in Sichuan |
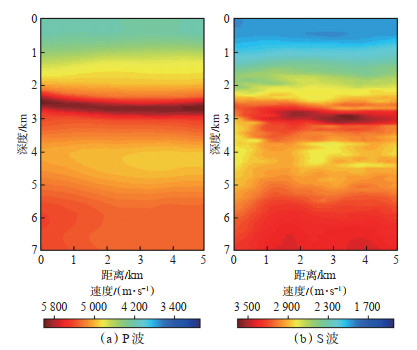
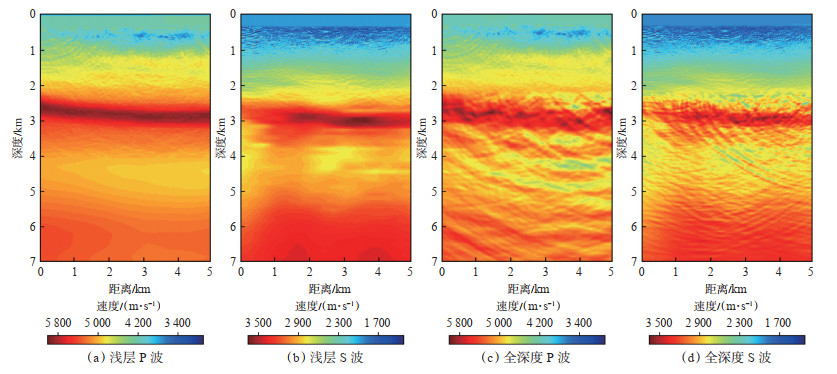
分层反演时,给定纵、横波初始速度场(图 8),采用0~1 s时窗反演深度为0~2 500 m的速度场。反演该深度时有限差分的空间采样间隔为15 m,反演更深的速度场时空间采样间隔为25 m。共选取300炮近偏移距数据参与浅层速度的反演,反演设置了5个频带,采用主频依次为6 Hz,10 Hz,15 Hz,20 Hz和25 Hz的雷克子波进行波场模拟。从浅层速度场的反演结果(图 9a,9b)来看,浅层速度场得到了有效更新。由于浅层速度已经被重建,与待反演的深层速度在交界位置产生了不耦合层,这将在下一步的反演中产生虚假反射影响深层速度建模,因此在反演深层速度场时,需要对该不耦合层进行光滑处理以降低虚假反射的影响。在平滑不耦合层后,固定浅层速度场,迭代更新深层速度,由于深度2 000 m附近的速度场被重新平滑,因此反演深层速度时需要从这一深度开始反演。深层速度场反演时采用了300炮的全偏移距全记录时长的数据,除空间采样间隔和所用地震数据范围外,所有的反演参数与浅层一致。从全速度场最终的反演结果(图 9c,9d)可以看出,浅、中、深层速度场均被更新,可见水平形态的构造趋势。
|
下载原图 图 8 四川某三维区块的初始速度场 Fig. 8 Initial velocity field of a 3D block in Sichuan |
|
下载原图 图 9 四川某三维区块分层反演后的速度场 Fig. 9 Velocity field after layered inversion of a 3 D block in Sichuan |
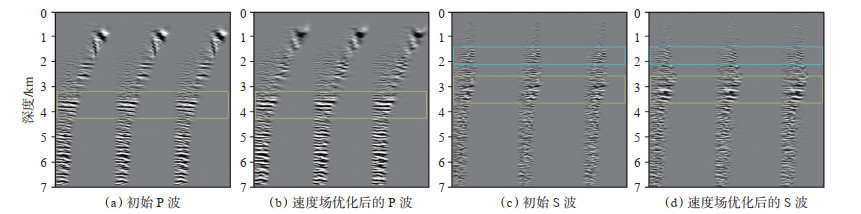
高斯束弹性波偏移共成像点(CIP)道集的拉平程度可用于验证速度场的精度,分别利用初始速度场和反演重建速度场进行偏移并抽取相同位置的共成像点道集进行对比,同相轴拉平程度高的对应速度场越精确。对比四川某工区实际资料的纵、横波共成像点道集可以看出,相比初始速度场,使用分层反演后的纵、横波速度偏移得到的共成像点道集同相轴拉平程度均更高、同相轴更清晰,能量亦更为集中,说明优化后速度场的精度更高(图 10)。
|
下载原图 图 10 四川某三维区块高斯束弹性波偏移共成像点(CIP)道集 Fig. 10 Common imaging point(CIP)gathers of Gaussian beam elastic wave migration of a 3D block in Sichuan |
(1)相较于常规的基于走时的反演方法,EFWI通过近似模拟地震波在弹性介质中的波动方程,充分利用地震信号的运动学和动力学特征进行反演,速度建模的精度更高。
(2)利用分层反演的策略,降低制约EFWI的非线性因素影响,提高浅层和中深层纵、横波速度反演的精度;改进的共轭梯度法可提高反演的稳定性,提高收敛速率。同时,改进的共轭梯度法隐含浅层和中深层速度场梯度能量的归一化,使深层的梯度相对提升,提高了深层速度的反演精度。
(3)分层反演策略,由浅到深,由近到远地选取地震资料,可减少反演过程中的非线性影响,提高反演准确性;还可兼顾浅层低速和深层高速采用大小不同的有限差分网格,在减少计算量的同时保证波场模拟的精度,从而提高反演速度场的精度。
| [1] |
卞爱飞, 於文辉, 周华伟. 频率域全波形反演方法研究进展. 地球物理学进展, 2010, 25(3): 982-993. BIAN Aifei, YU Wenhui, ZHOU Huawei. Progress in the frequency-domain full waveform inversion method. Progress in Geophysics, 2010, 25(3): 982-993. DOI:10.3969/j.issn.1004-2903.2010.03.037 |
| [2] |
刘振峰. 油气地震地质模型述评. 岩性油气藏, 2018, 30(1): 19-29. LIU Zhenfeng. Review on oil and gas seismogeology models. Lithologic Reservoirs, 2018, 30(1): 19-29. |
| [3] |
LAILLY P. The seismic inverse problem as a sequence of before stack migrations[C]. Philadelphia: SIAM Conference on Inverse Scattering, 1983: 206-220.
|
| [4] |
TARANTOLA A. Inversion of seismic reflection data in the acoustic approximation. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [5] |
TARANTOLA A. A strategy for nonlinear elastic wave inversion of seismic reflection data. Geophysics, 1986, 51(10): 1893-1903. DOI:10.1190/1.1442046 |
| [6] |
任浩然, 王华忠, 黄光辉. 地震波反演成像方法的理论分析与对比. 岩性油气藏, 2012, 24(5): 12-18. REN Haoran, WANG Huazhong, HUANG Guanghui. Theoretical analysis and comparison of seismic wave inversion and imaging methods. Lithologic Reservoirs, 2012, 24(5): 12-18. |
| [7] |
MORA P. Elastic wave-field inversion of reflection and transmission data. Geophysics, 1988, 53(6): 750-759. DOI:10.1190/1.1442510 |
| [8] |
PRATT R G. Seismic waveform inversion in the frequency domain, Part 1:Theory and verification in physical scale model. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [9] |
SHIN C, CHA Y H. Waveform inversion in the Laplace domain. Geophysical Journal International, 2008, 173(3): 922-931. DOI:10.1111/j.1365-246X.2008.03768.x |
| [10] |
HA W, SHIN C. Why do Laplace-domain waveform inversions yield long-wavelength results. Geophysics, 2013, 78(4): 167-173. DOI:10.1190/geo2012-0365.1 |
| [11] |
PARK E, HA W, CHUNG W, et al. 2D Laplace-domain waveform inversion of field data using a power objective function. Pure and Applied Geophysics, 2013, 170(12): 2075-2085. DOI:10.1007/s00024-013-0651-4 |
| [12] |
SHIN J, KIM Y, SHIN C, et al. Laplace-domain full waveform inversion using irregular finite elements for complex foothill environments. Journal of Applied Geophysics, 2013, 96(1): 67-76. |
| [13] |
胡光辉, 杜泽源, 何兵红, 等. 近地表复杂区早至波全波形反演建模技术与应用. 石油物探, 2019, 58(6): 811-818. HU Guanghui, DU Zeyuan, HE Binghong, et al. Full waveform inversion based on early arrival waves and its application in complex near-surface area. Geophysical Prospecting for Petroleum, 2019, 58(6): 811-818. DOI:10.3969/j.issn.1000-1441.2019.06.003 |
| [14] |
王永生, 胡杰, 张静, 等. 宽频勘探技术在柴北缘深层侏罗系勘探中的应用. 岩性油气藏, 2017, 29(6): 101-107. WANG Yongsheng, HU Jie, ZHANG Jing, et al. Wide-frequency prospecting technology and its application on deep-seated Jurassic exploration in northern margin of Qaidam Basin. Lithologic Reservoirs, 2017, 29(6): 101-107. |
| [15] |
王华忠, 王雄文, 王西文. 地震波反演的基本问题分析. 岩性油气藏, 2012, 24(6): 1-9. WANG Huazhong, WANG Xiongwen, WANG Xiwen. Analysis of the basic problems of seismic wave inversion. Lithologic Reservoirs, 2012, 24(6): 1-9. |
| [16] |
ZOU Fangyu, SHEN Li. On the convergence of weighted adagrad with momentum for training deep neural networks. Computer Science, 2018, 1-19. |
| [17] |
ZHANG Qingchen, ZHOU Hui, LI Qingqing, et al. Robust source-independent elastic full-waveform inversion in the time domain robust source-independent elastic FWI. Geophysics, 2016, 81(2): 29-44. |
| [18] |
BAUMSTEIN A, ANDERSON J, HINKLEY D, et al. Scaling of the objective function gradient for full wavefield inversion[G]. The 79th SEG Expanded Abstracts, 2009: 2243-2247.
|
| [19] |
王孝, 刘文卿, 曾华会, 等. 复杂区分层约束近地表建模方法及应用. 岩性油气藏, 2018, 30(4): 68-73. WANG Xiao, LIU Wenqing, ZENG Huahui, et al. Stratified constrained near-surface model building method and its application in complex surface area. Lithologic Reservoirs, 2018, 30(4): 68-73. |
 2023, Vol. 35
2023, Vol. 35



