2. 中国石油集团测井有限公司长庆分公司, 西安 710201
2. Changqing Branch, China Petroleum Group Logging Co., Ltd, Xi'an 710201, China
地层孔隙压力是页岩储层储量预测和评价页岩油气“甜点”优势储层的重要参数,对于钻井液密度和井身结构的确定也至关重要[1]。陇东地区页岩地层受复杂沉积及构造影响,通常呈现出孔隙结构复杂、非均质性较强等地质特征[2],而常规地层压力预测方法考虑的影响因素较为单一,预测精度往往达不到预期,严重阻碍了该区井位钻探、油气运移及油气成藏等研究工作[3]。因此,亟需寻求一种新方法以计算该区页岩地层压力。
岩层孔隙中的流体压力被称为地层压力,亦称为孔隙流体压力,是指由于沉积物的压实作用对地层孔隙流体产生的压力。1925年,Terzaghi提出了压实平衡定理及有效应力的概念,并将其引入岩体力学范畴,首次量化了地层压力[4]。1965年,Hott‐ mann等[5]首次提出了利用测井数据预测页岩孔隙压力的方法,即基于测井资料中的声波时差或电阻率与埋深的关系进行正常压实趋势线的建立,从而计算地层压力。1972年,Eaton [6]考虑了上覆岩层压力对地层压力的影响,以此建立了地层压力与声波时差的关系式,并建立了Eaton模型框架。等效深度法和Eaton法均是基于正常压实趋势线的建立,这类方法的缺点是人为误差较大且难以避免[7],针对这一问题,学者们陆续提出了基于有效应力理论的Bowers法、樊洪海综合法等[8-9],但该类方法需要考虑某些间接参数,地层压力预测结果的准确性也较难保证。随着数字化和智能化技术的不断发展,机器学习算法被陆续引入地层压力的预测研究中,杨进[10]基于BP神经网络井底下部地层的声波时差预测技术对地层压力进行了预测;Haris等[11]预测南苏门答腊油田地层压力时引入了概率神经网络(PNN);Ahmed等[12]基于人工神经网络(ANN),结合现场实际地层压力数据预测孔隙压力,随后又将支持向量机(SVM)引入到地层压力的预测中,取得了较好的应用效果[13]。此外,自适应神经模糊系统(ANFIS)、极限学习机、XGBoost等机器学习方法被陆续引入地层压力的预测研究中[14-16]。与传统地层压力预测方法相比,机器学习方法更客观,考虑的因素也更全面,且不会过于依赖某些特定参数的选取,避免了由人为因素产生的误差,工作效率和预测精度在一定程度上得到有效提升。然而,目前的机器学习算法仍存在一些问题,如模型训练时间较长、计算资源要求较高、不具备野外边缘计算的条件,且以往的地层压力智能预测方法通常使用单一的机器学习算法及测井数据,缺乏针对地层压力特点进行的模型改进和模型融合[17]。
基于以往的研究成果,以陇东地区延长组7段(长7段)页岩为研究目标,优选与地层压力关联度较高的测井响应参数并结合实测地层压力数据,采用基于斑马算法优化支持向量回归机进行参数优化及模型训练;在此基础上预测地层压力,并与粒子群优化算法、灰狼算法、蚁群算法等3种机器算法的优化精度进行对比,将压力预测结果与等效深度法、Eaton法、有效应力法等常规方法预测的结果进行对比,以期为页岩地层压力的预测提供新的途径和理论支持。
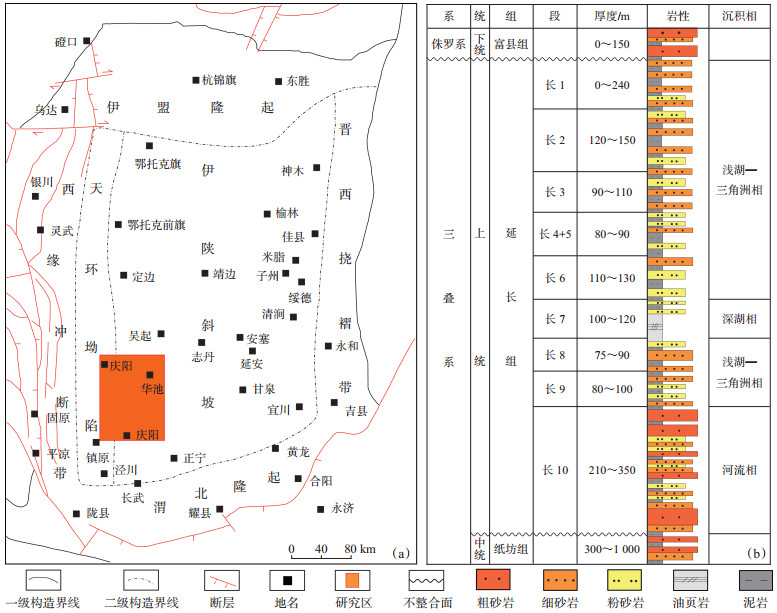
1 区域概况 1.1 地质特征鄂尔多斯盆地属于多构造旋回、多构造类型叠合的含油气盆地,地跨陕、甘、宁、蒙及晋五省,盆地内沉降较为稳定,坳陷迁移,构造相对简单[18]。陇东地区位于鄂尔多斯盆地西南部,页岩油气资源丰富,勘探潜力巨大,是石油勘探开发的热点领域[19]。研究区三叠系长7段形成于湖盆扩张的鼎盛时期,发育典型的陆相页岩油,是重要的生油层和页岩油层系,按岩性自上而下可划分出长7-1、长7-2和长7-3共3个小层[20]。其中,长7-1、长7-2小层是页岩油勘探开发的重点层段,岩性以夹层型(夹多期薄层粉—细砂岩)暗色泥页岩为主;长7-3小层目前处于勘探风险评估、原位转化攻关试验阶段,岩性以暗色泥岩、黑色页岩为主[21](图 1)。
|
下载原图 图 1 鄂尔多斯盆地陇东地区构造位置(a)及三叠系延长组岩性地层综合柱状图(b)(据文献[18] 修改) Fig. 1 Structural location(a)and stratigraphic column of Triassic Yanchang Formation(b)in Longdong area, Ordos Basin |
鄂尔多斯盆地中生界地层压力系数普遍较低,李士祥[22]通过统计盆地内三叠系延长组904个实测压力点得出地层压力系数主要为0.60~0.90,按照常用的地层压力分类方案,该地层压力以超低压和异常低压为主,其中陇东地区延长组压力系数主要为0.70~0.85,平均为0.78,属于超低压—异常低压地层,长7段压力系数为0.68~0.86,地层压力分布较为稳定(表 1)。
|
|
下载CSV 表 1 陇东地区三叠系长7段实测地层压力统计 Table 1 Statistical table of measured formation pressure of Triassic Chang 7 member in Longdong area |
针对陇东地区长7段页岩具有孔隙结构复杂、非均质性强的特征,提出了一种基于斑马算法优化支持向量回归机的页岩地层压力预测方法。支持向量回归机(SVR)具有较强的鲁棒性、泛化能力、灵活性和通用性,对于小样本的数据预测有较好的适用性;斑马优化算法(ZOA)相较于其他的优化算法具有更好的全局搜索能力、参数调节灵活性和并行性以及更快的收敛速度等优势,特别适用于参数较多、复杂度较高的优化问题。
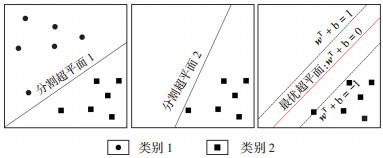
2.1 支持向量回归机算法1995年,Vapnik基于统计学习理论,结合结构风险最小化原则,提出了支持向量回归机算法(SVR)这一监督学习方法(图 2),旨在寻找一个最优的超平面来分隔不同类别的数据点,以解决分类、数据回归分析和预测等问题[23]。
|
下载原图 图 2 支持向量回归机算法的最优超平面示意图 Fig. 2 Optimal hyperplane of Support Vector Regression |
使用支持向量回归机进行地层压力预测属于解决回归问题,建立n维的输入参数 x与输出参数y之间的关系式:
| $ f(\boldsymbol{x})=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b $ | (1) |
式中:w为超平面的法向量;b为位移项(偏置)。
误差函数为
| $ |y-f(\boldsymbol{x}, \boldsymbol{w})|_{\varepsilon}=\left\{\begin{array}{cr} 0, & |y-f(\boldsymbol{x}, \boldsymbol{w})| \leqslant \varepsilon \\ |y-f(\boldsymbol{x}, \boldsymbol{w})|-\varepsilon, & otherwise \end{array}\right. $ | (2) |
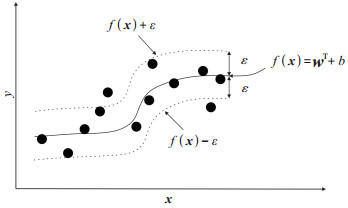
式(2)在图上表现为近视轨道的区域(图 3),该区域称为不敏感带,对区域内的数据不做惩罚;ε为该区域的带宽。
|
下载原图 图 3 支持向量回归机示意图 Fig. 3 Schematic of Support Vector Regression |
支持向量回归机(SVR)的最优化问题可表示为
| $ \begin{aligned} & \min \frac{1}{2}\|\boldsymbol{w}\|^2+C \sum\limits_{i=1}^l\left(\xi_i+\xi_i^*\right) \\ & \text { s.t. }\left\{\begin{array}{l} \boldsymbol{y}_i-\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_i-b \leqslant \varepsilon+\xi_i \\ \boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}_i+b-\boldsymbol{y}_i \leqslant \varepsilon+\xi_i^*, \quad i=1,2 \cdots, l \\ \xi_i>0, \quad \xi_i^*>0 \end{array}\right. \end{aligned} $ | (3) |
式中:C为惩罚参数;i为第i个样本;l为训练样本数,个;x,xi为任意2个样本向量;ξi和ξi*均为松弛变量,其中ξi* =| yi - f(xi,w)| - ε表示度量真实值与敏感带的距离,降低对超平面的要求。
引入拉格朗日乘子,根据卡罗需-库恩-塔克(KKT)条件及其补充条件,可得
| $ f(\boldsymbol{x}, \boldsymbol{w})=\sum\limits_{i=1}^l\left(a_i+a_i^*\right) \varphi(x)^{\mathrm{T}} \varphi\left(\boldsymbol{x}_i\right)^{\mathrm{T}}+b $ | (4) |
式中:ai和ai*均为拉格朗日乘子;φ(x) 为低维到高维的映射关系式。
为了将非线性特征变量线性化,引入核函数把非线性样本空间投射到高维线性特征空间,降低了非线性计算的难度,从而提高计算效率。核函数可表达为
| $ K\left(\boldsymbol{x}, \boldsymbol{x}_i\right)=\varphi(\boldsymbol{x})^{\mathrm{T}} \varphi\left(\boldsymbol{x}_i\right)^{\mathrm{T}} $ | (5) |
因此,式(4)可改为
| $ f(\boldsymbol{x}, \boldsymbol{w})=\sum\limits_{i=1}^l\left(a_i+a_i^*\right) K\left(\boldsymbol{x}, \boldsymbol{x}_i\right)+b $ | (6) |
常见的核函数有线性核函数、多项式核函数、高斯核函数、拉普拉斯核函数和Sigmoid核函数等,其中高斯核函数的收敛域、学习精度核计算性能均优于其他几种核函数。因此,优选高斯核函数作为本文的核函数。高斯核函数的表达式为
| $ K\left(\boldsymbol{x}, \boldsymbol{x}_i\right)=\exp \left[-\frac{\left(\boldsymbol{x}-\boldsymbol{x}_i\right)^2}{\sigma^2}\right] $ | (7) |
式中:σ > 0,为高斯核函数的带宽。
2.2 斑马优化算法Trojovská等[24]通过观察自然界中斑马群体独特的社会结构、避敌策略、信息传递、适应环境等生存行为模式,提出了一种启发式自适应优化算法——斑马优化算法(ZOA)。该方法模拟斑马的觅食行为和躲避捕食者攻击采用的防御策略,通过个体的相互作用和环境反馈实现位置更新来寻求待解问题的最优解,具有寻优能力强、收敛速度快等特点。
2.2.1 初始化同其他优化算法类似,在m维寻优空间里随机初始化N个斑马种群的位置:
| $ \boldsymbol{x}_{i, j}=l b_j+a\left(u_j-l_j\right), \quad i=1,2, \cdots, m $ | (8) |
式中:xi,j为第i匹斑马第j维位置;uj和lj分别为寻优上、下边界;a为随机数,取值0~1。
2.2.2 觅食行为在第一阶段,模拟斑马种群成员在搜索食物时的行为并进行更新。在ZOA中,种群中具有最优位置的成员被认为是先锋斑马,为使其他成员也能吃到食物,先锋斑马会引导其他种群成员走向其所处搜索空间中更好的觅食位置。因此,斑马在觅食阶段的位置更新可以用数学模型表示:
| $ \boldsymbol{x}_{i, j}^{\mathrm{new}, P_1}=\boldsymbol{x}_{i, j}+a\left(P Z_j-I \boldsymbol{x}_{i, j}\right) $ | (9) |
| $ \boldsymbol{X}_i=\left\{\begin{array}{lc} \boldsymbol{X}_i^{\text {new }, P_1}, & F_i^{\text {new }, P_1}<F_i \\ \boldsymbol{X}_i, & F_i^{\text {new }, P_1} \geqslant F_i \end{array}\right. $ | (10) |
式中:P1为第一阶段第i匹斑马新位置;xi,jnew,P1为第一阶段第i匹斑马第j维新位置;Xinew,P1为第一阶段第i匹斑马新位置;Xi为第i匹斑马位置;PZj为第j维先锋斑马位置;I为种群变化控制参数,值为1~2;Finew,P1为第一阶段第i匹斑马适应度值;Fi为第i匹斑马适应度值。
2.2.3 防御策略在第二阶段,模拟斑马对捕食者攻击的防御策略,更新斑马种群成员在搜索空间中的位置。斑马的防御策略会因捕食者的不同进行调整,假设以下2种防御策略发生的概率相同:Ⅰ.狮子攻击斑马,斑马以Z字形或随机的侧向转弯动作逃跑;Ⅱ.其他捕食者攻击斑马,斑马种群聚集在一起对捕食者达到迷惑和恐吓的目的。
| $ \boldsymbol{x}_{i, j}^{\mathrm{new}, P_2}= \begin{cases}S_1: \boldsymbol{x}_{i, j}+R(2 a-1)\left(1-\frac{t}{T_{\max }}\right) \boldsymbol{x}_{i, j}, & P_{\mathrm{s}} \leqslant 0.5 \\ S_2: \boldsymbol{x}_{i, j}+r\left(A Z_j-I \boldsymbol{x}_{i, j}\right), & P_{\mathrm{s}}>0.5\end{cases} $ | (11) |
| $ \boldsymbol{X}_i=\left\{\begin{array}{l} \boldsymbol{X}_i^{\text {new. }, P 2}, F_i^{\text {new }, P 2}<F_i \\ \boldsymbol{X}_i \quad, F_i^{\text {new. }, P_2} \geqslant F_i \end{array}\right. $ | (12) |
式中:S1和S2分别为斑马种群防御策略Ⅰ和Ⅱ;P2为防御阶段第i匹斑马新位置;xi,jnew,P2为第二阶段第i匹斑马第j维新位置;Xinew,P2为第二阶段第i匹斑马新位置;R为常数,取值0.01;PS为选择逃跑或进攻的概率,取值0~1;t,Tmax分别为ZOA当前迭代次数和最大迭代次数;AZj为第j维受攻击状态下的斑马位置;Finew,P2为第二阶段第i匹斑马适应度值。
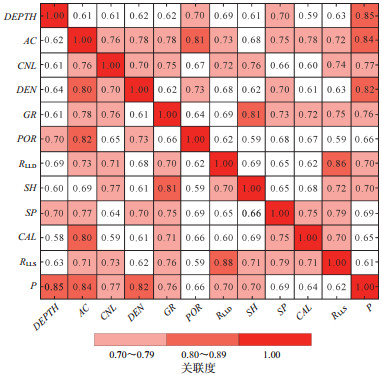
2.3 ZOA-SVR地层压力预测模型构建灰色关联分析方法是分析系统中各因素间关联程度的一种量化方法[25]。根据陇东地区长7段的实测地层压力,结合常规地层压力计算模型中的输入参数并综合考虑地层压力的影响因素,选取实测地层压力点处的深度(DEPTH)、声波时差(AC)、密度(DEN)、中子(CNL)、自然伽马(GR)、自然电位(SP)、孔隙度(POR)、深侧向电阻率(RLLD)、浅侧向电阻率(RLLS)、泥质含量(SH)、井径(CAL)等与实测地层压力数据(P)进行关联度分析。结果(图 4)显示,各参数与地层压力的关联度均大于0.55,其中DEPTH,AC,DEN,CNL,GR,RLLD,SH与地层压力的关联度均大于0.70。因此,本文选取这7个参数作为输入特征参数以预测研究区地层压力。其中,关联度计算公式为
| $ r_{0 i}=\frac{1}{n} \sum\limits_{k=1}^n \xi_{0 i}(k) \quad \xi_{0 i}(k)=\frac{\min\limits_i \min\limits_k\left|\boldsymbol{x}_0(k)-\boldsymbol{x}_i(k)\right|+\rho \max\limits_i \max\limits_k\left|\boldsymbol{x}_0(k)-\boldsymbol{x}_i(k)\right|}{\left|\boldsymbol{x}_0(k)-\boldsymbol{x}_i(k)\right|+\rho \max\limits_i \max\limits_k\left|\boldsymbol{x}_0(k)-\boldsymbol{x}_i(k)\right|} $ | (13) |
|
下载原图 图 4 陇东地区三叠系长7段特征参数与地层孔隙压力关联度热力图 Fig. 4 Heatmap of correlation between formation pore pressure and characteristic parameters of Triassic Chang 7 member in Longdong area |
式中:r0i为目标序列与第i个比较序列间的关联度;ξ0i(k)
为目标序列与第i个比较序列在第k个数据点时的关联系数;x0(k)、xi(k) 分别为目标序列、比较序列;| x0(k)- x i(k)|为目标序列与比较序列在第k点的绝对差值;
在支持向量回归机算法中使用的核函数为高斯核函数(RBF),而在高斯核函数中,惩罚因子C、核参数(带宽)σ为关键参数,通过优化算法迭代循环可以筛选出问题的最优解[26]。为提高支持向量回归机地层压力预测结果的精确性,利用斑马算法对参数进行优化。
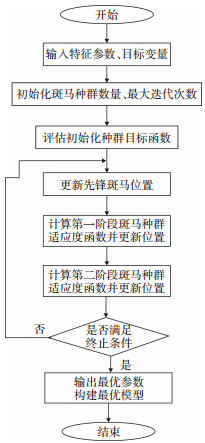
基于斑马算法优化支持向量回归机(ZOASVR)预测地层压力的具体实现流程(图 5)如下:
|
下载原图 图 5 基于斑马算法优化支持向量回归机(ZOA-SVR)预测页岩地层压力的流程图 Fig. 5 Flowchart of the ZOA-SVR program |
① 输入实测地层压力数据以及对地层压力响应明显的DEPTH,AC,DEN,CNL,GR,RLLD,SH等7个参数,前者为目标变量,后者为输入特征;
② 设置初始斑马种群的位置、种群数量和最大迭代次数;
③ 计算所有斑马种群适应度值,保存当前最佳斑马位置;
④ 执行觅食行为斑马位置更新算子、更新斑马位置,执行防御策略斑马位置更新算子、更新斑马位置;
⑤ 计算所有位置更新后的斑马适应度值,若满足终止条件则结束,否则重复直至满足算法终止条件;
⑥ 输出最优参数并构建最优SVR模型,利用模型预测研究区地层压力,以平均相对误差(MRE)对模型进行评价。
由于地层压力预测属于回归问题,而不是分类问题,因此选取预测值与实测值之间的平均相对误差是否达到最小设置值作为本文的适应度函数(停止条件),并以此为依据判断ZOA-SVR的预测精度。综上可构建出基于ZOA-SVR预测地层压力的最优化问题:
| $ \left\{\begin{array}{l} F_{\text {MSE }}(C, \sigma)=\min (M R E)=\min \frac{1}{h} \sum\limits_{i=1}^h\left|\frac{P_i^{\mathrm{t}}-P_i^{\mathrm{f}}}{P_i^{\mathrm{t}}}\right| \\ \text { s.t } \quad C \in\left[C_{\min }, C_{\max }\right], \quad \sigma \in\left[\sigma_{\min }, \sigma_{\max }\right] \end{array}\right. $ | (14) |
式中:FMSE为适应度函数;MRE为平均相对误差;h为总样本数量,个;Pit、Pif分别为第i个样本的实测、预测地层压力,MPa。
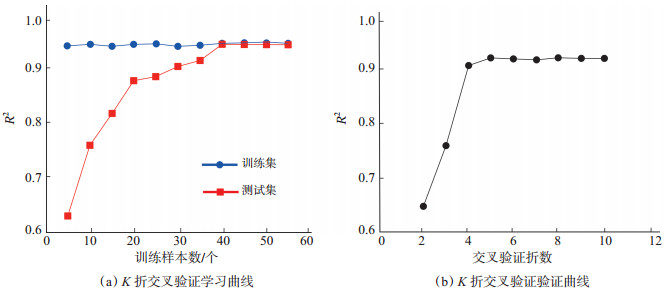
为避免机器学习在一定程度上出现数据过拟合和选择偏差的现象,即出现预测结果的偶然性,采用K折交叉验证的方式进行数据集的训练及预测,以此增强模型的泛化能力。可决系数R2在回归问题中是一个衡量模型拟合优度的指标;K折交叉验证中学习曲线是用来评估不同大小的训练集下模型的优劣程度,验证曲线则是根据不同的交叉验证中折叠的数量来评估模型的优劣。因此,选用R2结合交叉验证学习曲线和验证曲线来进一步确定数据集样本和模型参数(图 6),提高模型性能。
| $ R^2=1-\frac{\sum_{i=1}^h\left(y_i-\hat{y}_i\right)^2}{\sum_{i=1}^h\left(y_i-\bar{y}\right)^2} $ | (15) |
|
下载原图 图 6 陇东地区三叠系长7段ZOA-SVR模型评估曲线 Fig. 6 Model evaluation curve of ZOA-SVR for Triassic Chang 7 member in Longdong area |
式中:yi为观测值;ŷi为预测值;y为观测值的平均值。
结果(图 6)显示,当训练的样本数大于40时,R2收敛可达到0.9以上,且不会因训练样本数的变化而产生过拟合或欠拟合;当采用5折交叉验证时模型的性能达到最优。
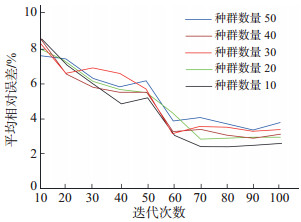
考虑样本数较少,分别设置斑马优化算法的迭代次数为10,20,30,40,50,60,70,80,90和100,分别设置初始斑马种群数量为10,20,30,40,50,以此研究不同种群数量下预测地层压力的平均相对误差随迭代次数的变化情况。结果(图 7)显示,当初始种群数量为10、最大迭代次数为70时,预测结果相较实测结果的平均相对误差最小,且当迭代次数继续增加时,平均相对误差趋于稳定。
|
下载原图 图 7 陇东地区三叠系长7段ZOA-SVR模型预测地层压力时不同种群数量下的平均相对误差-迭代次数交会图 Fig. 7 Cross plot of iteration count versus mean relative error for different population sizes of formation pressure based on ZOA-SVR model of Triassic Chang 7 member in Longdong area |
综合考虑问题复杂度、计算资源和算法收敛性等因素,确定训练样本数为40,交叉验证折数为5;设置初始化斑马种群数量为10,最大迭代次数为70。
3 应用及效果分析 3.1 误差分析利用斑马优化算法(ZOA)、粒子群优化算法(PSO)、灰狼算法(GWO)、蚁群算法(ACO)分别对SVR中的C和σ进行参数优化。结果(表 2)显示,ZOA-SVR模型的R2最高,为0.942,表明了支持向量回归机中的C和σ对于地层压力预测精度的重要性,也进一步说明了ZOA相较于其他优化算法在陇东区页岩地层预测中更具优势。
|
|
下载CSV 表 2 陇东地区三叠系长7段ZOA与3种优化算法支持向量回归机模型的参数优化结果对比 Table 2 Comparison of parameter optimization results of ZOA and three optimization algorithms for three SVR model of Triassic Chang 7 member in Longdong area |
利用构建的ZOA-SVR模型对研究区地层压力进行预测,并将预测结果与等效深度法、Eaton法、有效应力法3种常规的地层压力预测方法预测结果进行对比。结果(表 3)显示,无论是在训练集样本还是测试集样本,ZOA-SVR模型的预测精度都有大幅提升,预测测试集地层压力的平均相对误差低至2.42%,相较于等效深度法、Eaton法、有效应力法分别降低了32.53%,15.31%,5.91%。
|
|
下载CSV 表 3 陇东地区三叠系长7段ZOA-SVR方法与3种常规地层压力预测方法相对误差对比 Table 3 Comparison of relative errors between ZOA-SVR method and three conventional formation pressure prediction methods of Triassic Chang 7 member in Longdong area |
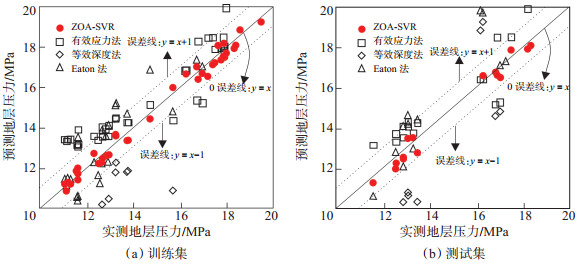
将3种常规方法和ZOA-SVR的预测地层压力与实际地层压力在训练集和测试集上进行交会,结果(图 8)显示,ZOA-SVR的预测结果在训练集和测试集上均集中在0误差线附近,且绝对误差均低于1 MPa,进一步印证了该模型的可靠性。
|
下载原图 图 8 陇东地区三叠系长7段ZOA-SVR及常规方法地层压力预测误差对比图 Fig. 8 Comparison of formation pressure prediction errors between ZOA-SVR and conventional methods of Triassic Chang 7 member in Longdong area |
以陇东合水地区评价井Z356井为例,该井长7段共有4个实测地层压力点,对这4个压力点分别采用等效深度法、Eaton法、有效应力法等3种常规方法及PSO-SVR,GWO-SVR,ACO-SVR和ZOA-SVR等4种机器算法进行地层压力预测,并将预测结果与实测压力进行对比。结果(表 4、表 5、图 9)显示,4种机器学习方法预测的地层压力整体误差均不大,且更优于3种常规方法,其中ZOA-SVR模型预测的地层压力结果最优,与实测地层压力数据基本吻合;ZOA-SVR预测结果显示该井长7段地层压力在垂向上分布较为稳定,其中泥页岩段地层压力高于砂岩段的地层压力,地层压力系数主要为0.70~0.80,整体上属于异常低压环境,与实际地层情况相符。
|
|
下载CSV 表 4 陇东地区Z356井三叠系长7段ZOA-SVR及常规方法预测地层压力结果对比 Table 4 Comparison of predicting formation pressure between ZOA-SVR and conventional methods of Triassic Chang 7 member in Z356 well in Longdong area |
|
|
下载CSV 表 5 陇东地区Z356井三叠系长7段ZOA-SVR及3种机器学习法预测的地层压力结果对比 Table 5 Statistical table for the comparison of predicting formation pressure between ZOA-SVR and three machine learn‐ ing of Triassic Chang 7 member in Z356 well in Longdong area |

|
下载原图 图 9 陇东地区Z356井三叠系长7段地层压力预测结果对比 Fig. 9 Comparison of formation pressure prediction results of Triassic Chang 7 member in Z356 well |
以陇东华池地区评价井Y94井为例,该井长7段共有4个实测地层压力点,对这4个压力点分别采用等效深度法、Eaton法、有效应力法等3种常规方法及PSO-SVR,GWO-SVR,ACO-SVR和ZOA-SVR等4种机器算法对地层压力进行预测,并将预测结果与实测地层压力进行对比。结果(表 6、表 7、图 10)显示,ZOA-SVR模型预测的地层压力结果与实测地层压力数据基本吻合,更优于其他方法;该井地层压力在垂向上分布较为稳定,泥页岩段地层压力高于砂岩段地层压力,地层压力系数主要为0.80~0.90,整体上属于异常低压环境,与实际地层情况相符。
|
|
下载CSV 表 6 陇东地区Y94井三叠系长7段ZOA-SVR及常规方法预测地层压力结果对比 Table 6 Statistical table of formation pressure prediction results using conventional methods of Triassic Chang 7 member of Y94 well in Longdong area |
|
|
下载CSV 表 7 陇东地区Y94井三叠系长7段ZOA-SVR及3种机器学习法预测的地层压力结果对比 Table 7 Statistical table of formation pressure prediction results using machine learning of Triassic Chang 7 member of Y94 well in Longdong area |

|
下载原图 图 10 陇东地区Y94井三叠系长7段地层压力预测结果对比 Fig. 10 Comparison of formation pressure prediction results of Triassic Chang 7 member in Y94 well in Longdong area |
(1)采用ZOA-SVR模型并将实测地层压力数据作为目标变量,优选与陇东地区长7段地层压力关联度达到0.70以上的DEPTH,AC,DEN,CNL,GR,RLLD,SH等7个参数作为输入特征参数,设置训练样本数为40,交叉验证折数为5,初始化斑马种群数量为10,最大迭代次数为70,对惩罚因子和核参数进行优化后建模,地层压力参数的拟合优度指标R2达到0.942,平均相对误差为2.42%,绝对误差均低于1 MPa。
(2)ZOA-SVR模型与基于PSO,GWO,ACO等3种机器学习算法建立的模型相比,R2分别提高了0.209,0.327,0.142,地层压力预测结果与实际地层压力数据的相对误差比等效深度法、Eaton法、有效应力法分别降低了32.53%,15.31%,5.91%。
(3)ZOA-SVR模型预测结果显示,陇东地区长7段地层压力在垂向上分布较稳定,泥页岩段地层压力高于砂岩段,地层压力系数主要为0.80~0.90,整体上属于异常低压环境,与实际地层情况相符。
| [1] |
瞿建华, 王泽胜, 任本兵, 等. 准噶尔盆地环玛湖斜坡区异常高压成因机理分析及压力预测方法. 岩性油气藏, 2014, 26(5): 36-39. QU Jianhua, WANG Zesheng, REN Benbing, et al. Genetic mechanism analysis and prediction method of abnormal high pressure in Mahu slope area, Junggar Basin. Lithologic Reservoirs, 2014, 26(5): 36-39. |
| [2] |
肖玲, 陈曦, 雷宁, 等. 鄂尔多斯盆地合水地区三叠系长7段页岩油储层特征及主控因素. 岩性油气藏, 2023, 35(2): 80-93. XIAO Ling, CHEN Xi, LEI Ning, et al. Characteristics and main controlling factors of shale oil reservoirs of Triassic Chang 7 member in Heshui area, Ordos Basin. Lithologic Reservoirs, 2023, 35(2): 80-93. |
| [3] |
杨韬政, 刘成林, 田继先, 等. 柴达木盆地大风山凸起地层压力预测及成因分析. 岩性油气藏, 2023, 35(1): 96-107. YANG Taozheng, LIU Chenglin, TIAN Jixian, et al. Prediction and genesis of formation pressure in Dafengshan uplift, Qaidam Basin. Lithologic Reservoirs, 2023, 35(1): 96-107. |
| [4] |
BRUCE B. An introduction to this special section: Pore pressure. The Leading Edge, 2002, 21(2): 169-177. DOI:10.1190/1.1452606 |
| [5] |
HOTTMANN C E, JOHNSON R K. Estimation of formation pressures from log-derived shale properties. Journal of Petroleum Technology, 1965, 17(6): 717-722. DOI:10.2118/1110-PA |
| [6] |
EATON B A. The effect of overburden stress on geopressure prediction from well logs. Journal of Petroleum Technology, 1972, 24(8): 929-934. DOI:10.2118/3719-PA |
| [7] |
李玉凤, 孙炜, 何巍巍, 等. 基于叠前反演的泥页岩地层压力预测方法. 岩性油气藏, 2019, 31(1): 113-121. LI Yufeng, SUN Wei, HE Weiwei, et al. Prediction method of shale formation pressure based on pre-stack inversion. Lithologic Reservoirs, 2019, 31(1): 113-121. |
| [8] |
BOWERS G L. Pore pressure estimation from velocity data: Accounting for overpressure mechanisms besides under compaction. SPE Drilling & Completion, 1995, 10(2): 89-95. |
| [9] |
樊洪海. 利用声速检测欠压实泥岩异常高压的简易方法与应用. 石油钻探技术, 2001, 29(5): 9-11. FAN Honghai. A simple pore pressure estimation method for a disequilibrium compaction shale using sonic velocity. Petroleum Drilling Techniques, 2001, 29(5): 9-11. |
| [10] |
杨进. 地层压力BP网络预测方法研究及其应用. 石油钻采工艺, 2003, 25(3): 13-15. YANG Jin. Study on formation pressure prediction with BP network and its application. Oil Drilling & Production Technology, 2003, 25(3): 13-15. |
| [11] |
HARIS A, SITORUS R J, RIYANTO A. Pore pressure prediction using probabilistic neural network: Case study of South Sumatra Basin. IOP Conference Series: Earth and Environmental Science, 2017, 62(1): 012021. |
| [12] |
AHMED A, ELKATATNY S, ALI A, et al. New model for pore pressure prediction while drilling using artificial neural networks. Arabian Journal for Science & Engineering, 2019, 44(6): 6079-6088. |
| [13] |
ABDULMALEK A S, MAHMOUD A A, ELKATATNY S, et al. Prediction of pore and fracture pressures using support vector machine[R]. Virtual: International Petroleum Technology Conference, 2019.
|
| [14] |
ANDRIAN D, ROSID M S, SEPTYANDY M R. Pore pressure prediction using Anfis method on well and seismic data field "Ayah". IOP Conference Series: Materials Science and Engineering, 2020, 854(1): 012-041. |
| [15] |
FARSI M, MOHAMADIAN N, GHORBANI H, et al. Predicting formation pore-pressure from well-log data with hybrid machine learning optimization algorithms. Natural Resources Research, 2021, 30(5): 3455-3481. |
| [16] |
PICHITA B, THANANYA R, PAKAWAT P, et al. Pore pressure estimation by using machine learning model[R]. Virtual: International Petroleum Technology Conference, 2021.
|
| [17] |
杨琼. 基于机器学习算法的地层压力智能预测及参数优选[D]. 北京: 中国石油大学(北京), 2024. YANG Qiong. Intelligent prediction of formation pressure and parameter optimization based on machine learning algorithm [D]. Beijing: China University of Petroleum(Beijing), 2024. |
| [18] |
文志刚, 罗雨舒, 刘江艳, 等. 陇东地区三叠系长7段页岩油储层孔隙结构特征及成因机制. 岩性油气藏, 2022, 34(6): 47-59. WEN Zhigang, LUO Yushu, LIU Jiangyan, et al. Pore structure characteristics and genetic mechanism of Triassic Chang 7 shale oil reservoir in Longdong area. Lithologic Reservoirs, 2022, 34(6): 47-59. |
| [19] |
沈健. 鄂尔多斯盆地陇东地区致密砂岩储层碳酸盐胶结物特征及成因机理. 岩性油气藏, 2020, 32(2): 24-32. SHEN Jian. Carbonate cementation characteristics and genetic mechanism of tight sandstone reservoirs in Longdong area, Ordos Basin. Lithologic Reservoirs, 2020, 32(2): 24-32. |
| [20] |
曹江骏, 王茜, 王刘伟, 等. 鄂尔多斯盆地合水地区三叠系长7段夹层型页岩油储层特征及主控因素. 岩性油气藏, 2024, 36(3): 158-171. CAO Jiangjun, WANG Xi, WANG Liuwei, et al. Characteristics and main controlling factors of interbedded shale oil reservoirs of Triassic Chang 7 member in Heshui area, Ordos Basin. Lithologic Reservoirs, 2024, 36(3): 158-171. |
| [21] |
张才利, 刘新社, 杨亚娟, 等. 鄂尔多斯盆地长庆油田油气勘探历程与启示. 新疆石油地质, 2021, 42(3): 253-263. ZHANG Caili, LIU Xinshe, YANG Yajuan, et al. Petroleum exploration history and enlightenment of Changqing oil field in Ordos Basin. Xinjiang Petroleum Geology, 2021, 42(3): 253-263. |
| [22] |
李士祥. 鄂尔多斯盆地中生界异常低压成因及对成藏的影响[D]. 成都: 成都理工大学, 2019. LI Shixiang. Effects on petroleum accumulation and genesis of the Mesozoic abnormal low pressure in Ordos Basin[D]. Chengdu: Chengdu University of Technology, 2019. |
| [23] |
宋宣毅, 刘月田, 马晶, 等. 基于灰狼算法优化的支持向量机产能预测. 岩性油气藏, 2020, 32(2): 134-140. SONG Xuanyi, LIU Yuetian, MA Jing, et al. Productivity forecast based on support vector machine optimized by grey wolf optimizer. Lithologic Reservoirs, 2020, 32(2): 134-140. |
| [24] |
TROJOVSKÁ E, DEHGHANI M TROJOVSKÝ P. Zebra optimization algorithm: A new bio-inspired optimization algorithm for solving optimization algorithm. IEEE Access, 2022(10): 49445-49473. |
| [25] |
周庆. 基于灰色主成分的聚合物驱操作成本预测方法. 岩性油气藏, 2012, 24(5): 116-119. ZHOU Qing. Prediction method of polymer flooding operation cost based on gray principal component analysis. Lithologic Reservoirs, 2012, 24(5): 116-119. |
| [26] |
刘明明, 王全, 马收, 等. 基于混合粒子群算法的煤层气井位优化方法. 岩性油气藏, 2020, 32(6): 164-171. LIU Mingming, WANG Quan, MA Shou, et al. Well placement optimization of coalbed methane based on hybrid particle swarm optimization algorithm. Lithologic Reservoirs, 2020, 32(6): 164-171. |
 2024, Vol. 36
2024, Vol. 36



