2. 中国石油大学(北京)地球物理学院, 北京 102249
2. School of Geophysics, China University of Petroleum (Beijing), Beijing 102249, China
地震反演始于20世纪60年代,经过六十多年的发展,现有的反演理论已较为成熟,地震反演结果精度也取得了较大提升,能够较真实地反映地下介质的情况 [1]。由于地震反演问题充满不确定性和多解性,通常需要给反演目标泛函施加正则化约束项,根据实现方式可分为稀疏约束反演、地质统计学反演和人工智能反演等 [2-4]。渤海湾盆地渤中凹陷古近系广泛发育扇三角洲沉积,具备丰富的油气勘探前景 [5-6],勘探实践表明,渤中凹陷石臼坨凸起构造带扇三角洲沉积发育多期叠置砂体,但砂体单层厚度小、横向展布变化快 [7],同时受到该区钻井较少、目的层地震资料分辨率较低等问题制约,对古近系储层的刻画多以
以渤中凹陷石臼坨凸起构造带古近系东营组二段为例,基于多尺度地震信号,提出一种地震分频多级稀疏正则化反演方法,利用匹配追踪与Wigner-Ville分布(MP-WVD)时频方法将地震信号分解为三级尺度;基于稀疏理论和贝叶斯理论,对不同尺度地震信号进行分级约束,以期能够提高反演精度,增强薄砂岩储层识别的可靠性。
1 方法原理 1.1 MP与Wigner-Ville分布原理利用地震分频属性来预测储层精度的关键是谱分解的时频分辨率,匹配追踪方法(MP)-Wigner-Ville(WVD)是一种无Heisenberg不确定原理限制的高时频分辨率谱分解技术,其中MP是关键的信号分解算法,WVD是频谱计算算法,MP将地震信号分解为一系列预定义的小波原子的线性叠加 [25]。
| $ \boldsymbol{s}=\operatorname{Re}\left[\sum\limits_{n=1}^{N} c_{n} \boldsymbol{m}_{n}+\boldsymbol{r}_{N}\right] $ | (1) |
式中:
| $ \boldsymbol{m}_{n}=\exp \left[-4 \ln 2\left(\frac{f_{n}^{2}}{k_{n}^{2}}\right)\left(t-u_{n}\right)^{2}+\mathrm{i} 2 {\rm{\mathsf{π}}} f_{n}\left(t-u_{n}\right)\right] $ | (2) |
| $ u_{n}=\arg \max\limits_{t}\left\{\operatorname{Env}\left[\boldsymbol{r}_{n-1}(t)\right]\right\} $ | (3) |
| $ \left(k_{n}, f_{n}\right)=\arg \max\limits_{\substack{k \in D_{k} \\ f \in D_{f}}} \frac{\left|\boldsymbol{r}_{n-1}(t) \boldsymbol{m}_{n}\left(t, u_{n}, k, f\right)\right|}{\boldsymbol{m}_{n}\left(t, u_{n}, k, f\right)_{2}} $ | (4) |
式中:
| $ D_{f}=\left[f_{u}-R_{f}, f_{u}+R_{f}\right] $ | (5) |
式中:
式(1)中,
| $ c_{n}=\left(\boldsymbol{m}_{n}^{\mathrm{T}} \boldsymbol{m}_{n}+\varepsilon\right)^{-1} \boldsymbol{m}_{n}^{\mathrm{T}} \boldsymbol{r}_{n-1} $ | (6) |
式中:
| $ \begin{align*} & \boldsymbol{A}(t, f)= \\ & \sum\limits_{n=1}^{N} \frac{4\left\{\left[\operatorname{Re}\left(c_{n}\right)\right]^{2}+\left[\operatorname{Im}\left(c_{n}\right)\right]^{2}\right\} \mathrm{e}^{\left.-\frac{{\rm{\mathsf{π}}}^{2} k_{n}^{2}\left(f-f_{n}\right)^{2}}{2 \ln f_{n}^{2}}-\frac{8 \ln 2 f_{n}^{2}\left(t-u_{n}\right)}{k_{n}^{2}}\right]}}{1+\mathrm{e}^{\left(\frac{-{\rm{\mathsf{π}}}^{2} k_{n}^{2}}{2 \ln 2}\right)} \cos \left\{\arctan \left[\frac{\operatorname{Im}\left(c_{n}\right)}{\operatorname{Re}\left(c_{n}\right)}\right]\right\}} \end{align*} $ | (7) |
式中:
基于线性化波阻抗正演理论,地震波单道合成记录
| $ s_{\mathrm{syn}}(t)=w(t) * r_{\mathrm{s}}(t)+l(t) $ | (8) |
式中:
| $ r_{\mathrm{s}}\left(t_{j}\right)=\frac{z\left(t_{j+1}\right)-z\left(t_{j}\right)}{z\left(t_{j+1}\right)+z\left(t_{j}\right)} \approx \frac{1}{2}\left\{\ln \left[z\left(t_{j+1}\right)\right]-\ln \left[z\left(t_{j}\right)\right]\right\} $ | (9) |
式中:
将式带入式,并写成矩阵形式,可得
| $ \boldsymbol{S}_{\text {syn }}=\boldsymbol{W D Z+L} $ | (10) |
式中:
| $ \boldsymbol{D}=\frac{1}{2}\left[\begin{array}{ccccc} -1 & 1 & & & \\ & -1 & 1 & & \\ & & \ddots & \ddots & \\ & & & -1 & 1 \end{array}\right] $ | (11) |
基于贝叶斯理论,地震波观测数据
| $ \mathrm{P}\left(\boldsymbol{Z} \mid S_{\text {obs }}\right)=\frac{\mathrm{P}\left(S_{\text {obs }} \mid \boldsymbol{Z}\right) \mathrm{P}\left(S_{\text {obs }}\right)}{\mathrm{P}(\boldsymbol{Z})} $ | (12) |
式中:
通常,假设
| $ \mathrm{P}\left(S_{\text {obs }} \mid \boldsymbol{Z}\right)=\frac{1}{(\sqrt{2 {\rm{\mathsf{π}}}})^{K+N_{w}-2} \boldsymbol{C}_{\mathrm{e}}} \mathrm{e}^{\left[-\frac{1}{2}\left(S_{\text {dath }}-W D Z\right)^{\mathrm{T}} \mathrm{C}_{\mathrm{e}}^{-1}\left(S_{\text {doc }}-W D Z\right)\right]} $ | (13) |
式中:
通常,假设地层中的波阻抗参数符合高斯分布,模型参数的先验分布表示为
| $ \mathrm{P}(\boldsymbol{Z})=\frac{1}{(\sqrt{2 {\rm{\mathsf{π}}}})^{k} \boldsymbol{C}_{\mathrm{Z}}} \mathrm{e}^{\left[-\frac{1}{2} \phi(\boldsymbol{Z})^{\mathrm{T}} \boldsymbol{C}_{\mathrm{Z}}^{-1} \phi(\boldsymbol{Z})\right]} $ | (14) |
式中:
| $ \mathrm{P}\left(\boldsymbol{Z} \mid \boldsymbol{S}_{\text {obs }}\right) \propto \mathrm{e}^{\left[-\frac{1}{2}\left(\boldsymbol{S}_{\text {olm }}-\boldsymbol{W} \boldsymbol{D} \boldsymbol{Z}\right)^{\mathrm{T}} \boldsymbol{C}_{\mathrm{e}}^{-1}\left(S_{\text {dats }}-\boldsymbol{W} \boldsymbol{D} \boldsymbol{Z}\right)-\frac{1}{2} \lambda \phi(\boldsymbol{Z})^{\mathrm{T}} \boldsymbol{C}_{\mathrm{Z}}^{-1} \phi(\boldsymbol{Z})\right]} $ | (15) |
式中:
对式(15)进一步进行整理,得到地震反演的目标函数:
| $ \begin{gather*} J(\boldsymbol{Z})=\frac{1}{\sigma_{\mathrm{e}}^{2}}\left(\boldsymbol{S}_{\text {obs }}-\boldsymbol{W} \boldsymbol{D} \boldsymbol{Z}\right)^{\mathrm{T}}\left(\boldsymbol{S}_{\text {obs }}-\boldsymbol{W} \boldsymbol{D} \boldsymbol{Z}\right)+ \\ \lambda \frac{1}{\sigma_{\rm Z}^{2}} \phi(\boldsymbol{Z})^{\mathrm{T}} \phi(\boldsymbol{Z})\end{gather*} $ | (16) |
式中:传统反演方法中
| $ \phi(\boldsymbol{Z})=\left(\boldsymbol{Z}-\boldsymbol{Z}_{\mathrm{ref}}\right) $ | (17) |
基于式,构建地震分频多级稀疏正则化反演目标函数,具体如下:
| $ \left\{\begin{array}{c} J_{\mathrm{b}}(\boldsymbol{Z})=\frac{1}{\sigma_{\text {eb }}^{2}}\left(\boldsymbol{S}_{\mathrm{b}}-\boldsymbol{W}_{\mathrm{b}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{b}}\right)^{\mathrm{T}}\left(\boldsymbol{S}_{\mathrm{b}}-\boldsymbol{W}_{\mathrm{b}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{b}}\right) \\ \quad+\lambda_{\mathrm{b}} \frac{1}{\sigma_{\text {zb }}^{2}}\left\|\boldsymbol{Z}_{\mathrm{b}}-\boldsymbol{Z}_{\text {ref } \_\mathrm{b}}\right\|_{2}^{2}+\beta_{\mathrm{b}}\left\|\boldsymbol{D} \boldsymbol{Z}_{\mathrm{b}}\right\|_{2}^{2} &(A)\\ J_{\mathrm{m}}(\boldsymbol{Z})=\frac{1}{\sigma_{\text {em }}^{2}}\left(\boldsymbol{S}_{\mathrm{m}}-\boldsymbol{W}_{\mathrm{m}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{m}}\right)^{\mathrm{T}}\left(\boldsymbol{S}_{\mathrm{m}}-\boldsymbol{W}_{\mathrm{m}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{m}}\right) \\ +\lambda_{\mathrm{m}} \frac{1}{\sigma_{\text {zm }}^{2}}\left\|\boldsymbol{Z}_{\mathrm{m}}-\boldsymbol{Z}_{\text {ref } \_\mathrm{m}}\right\|_{2}^{2}+\gamma_{\mathrm{m}}\left\|\boldsymbol{Z}_{\mathrm{m}}-\boldsymbol{Z}_{\mathrm{b}}\right\|_{2}^{2}+\beta_{\mathrm{m}}\left\|\boldsymbol{D} \boldsymbol{Z}_{\mathrm{m}}\right\|_{1} &(B)\\ J_{\mathrm{s}}(\boldsymbol{Z})=\frac{1}{\sigma_{\text {es }}^{2}}\left(\boldsymbol{S}_{\mathrm{s}}-\boldsymbol{W}_{\mathrm{s}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{s}}\right)^{\mathrm{T}}\left(\boldsymbol{S}_{\mathrm{s}}-\boldsymbol{W}_{\mathrm{s}} \boldsymbol{D} \boldsymbol{Z}_{\mathrm{s}}\right) \\ +\lambda_{\mathrm{s}} \frac{1}{\sigma_{\text {zs }}^{2}}\left\|\boldsymbol{Z}_{\mathrm{s}}-\boldsymbol{Z}_{\text {ref_} \mathrm{s}}\right\|_{2}^{2}+\gamma_{\mathrm{s}}\left\|\boldsymbol{Z}_{\mathrm{s}}-\boldsymbol{Z}_{\mathrm{m}}\right\|_{2}^{2}+\beta_{\mathrm{s}}\left\|\boldsymbol{D} \boldsymbol{Z}_{\mathrm{s}}\right\|_{0} &(C)\end{array}\right. $ | (18) |
式中:
L0范数凸表面积最小(图 1a),稀疏性最强,抗噪性也最强,属于典型非确定性多项式问题,计算复杂,耗时高。L1范数的凸面积介于L0和L2之间(图 1b),常作为L0范数的最优凸近似,比L0范数更加容易优化求解。L2范数凸面积最大(图 1c),稳定性高,最易求解。从反演精度和计算耗时两方面进行综合考虑,低分辨率大尺度信号选用同样精度低但计算快的L2范数约束;中尺度信号稀疏性一般,集中了最多峰值频率信号,选用L1范数约束;小尺度信号信噪比最低,存在大量有效的高频波阻抗信息,选用L0范数约束。
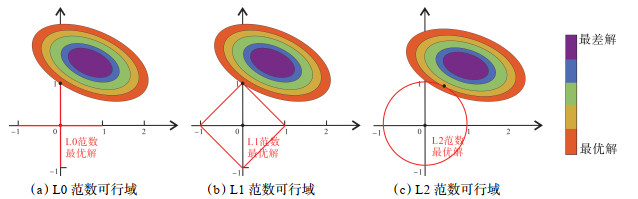
|
下载原图 图 1 范数可行域分析 Fig. 1 Feasible region analysis for different norms |
由于目标函数中存在多组正则化参数,联合L曲线法和试错法确定最优的正则化参数组合,以获取准确性高且分辨率高的反演结果。目标函数[式(18-A)]通过共轭梯度法计算;[式(18-B)]中存在L1正则化项,采用迭代重加权最小二乘法求解 [29];[式(18-C)]中存在L0正则化项,采用分裂布雷格曼方法 [30]。
首先,对叠后地震数据进行MP-VMD谱分解,根据时频能量分布将原始地震数据重构成大、中和小尺度信号;其次,利用3个不同尺度测井数据分别约束3个尺度的地震信号,从大尺度项目标函数向小尺度目标函数项进行逐级约束求解;最后,地震反演结果以小尺度项目标函数求解结果为准。具体流程如图 2所示。
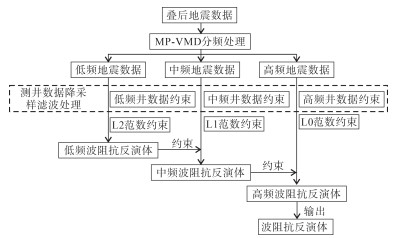
|
下载原图 图 2 地震分频多级稀疏正则化反演流程 Fig. 2 Flowchart of multi-level sparse regularization inversion of seismic frequency division |
根据地震信号的多尺度特征,构建多级旋回复合模型(图 3a),模型中存在2套大尺度旋回体、2套中尺度旋回体、2套小尺度旋回体。根据褶积理论,利用30 Hz雷克子波合成地震记录(图 3b)。
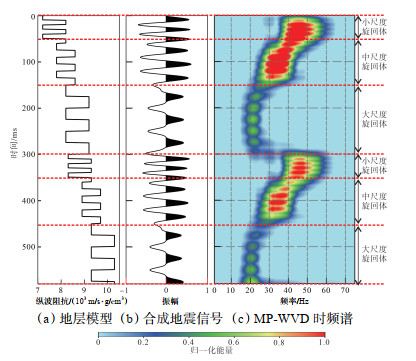
|
下载原图 图 3 多级旋回复合模型 Fig. 3 Multi-level rotation-coupled model |
由于地震波在传递过程中会存在调谐效应,难以直接从地震信号中直接剥离出不同旋回体对应的地震响应,而高精度时频分析方法能有效刻画地震信号中各时刻频率能量特征,进而提高不同旋回体的识别精度,因此,时频能量的精度直接决定了分频结果的好坏。建立MP-WVD时频谱(图 3c),将合成记录分为大尺度旋回体信号(频率为6~ 25 Hz)、中尺度旋回体(频率为25~40 Hz)及小尺度旋回体(频率为40~75 Hz);MP-WVD时频结果的能量团时间宽度与波阻抗模型时间域宽度一致,这也说明MP-WVD时频谱的可靠性。
与连续小波变换时频谱、S变换时频谱相比,MP-WVD时频谱中能量集中性较强,时间和频率方向的分辨率都更高;与WVD变换时频谱相比,MP-WVD时频分析是通过匹配追踪进行原子分解后,再进行WVD变换,有效克服了交叉项的干扰(图 4)。因此,MP-WVD时频谱更适用于地震信号分频处理。
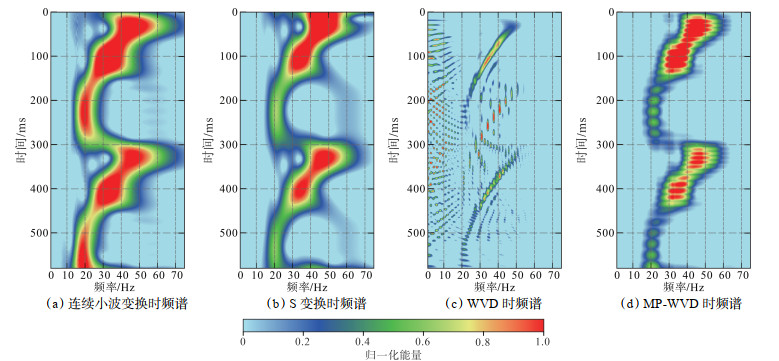
|
下载原图 图 4 多级旋回复合模型不同时频分析方法对比 Fig. 4 Comparison of different time-frequency analysis methods based on the multi-level rotation-coupled model |
地震信号的时频分析能够有效揭示地震信号中各个频率段对应的信号,并加强其重构的性质,对地震信号中的高低频率信号进行分频处理,最终获得地震信号分频体。基于MP-VMD时频分解和重构原理,对合成记录时频谱高、中和低频率范围的小波原子进行叠加,得到多尺度地震信号分频结果。其中,大尺度信号分频结果能够明显反映模型中的大套厚层地层响应特征,地震波长较长;厚度中等地层的地震响应主要集中在中尺度地震信号分频体中,地震波长适中;厚度较小的地层主要对应地震信号的高频部分,与小尺度地震信号对应较好,地震波长较短(图 5)。
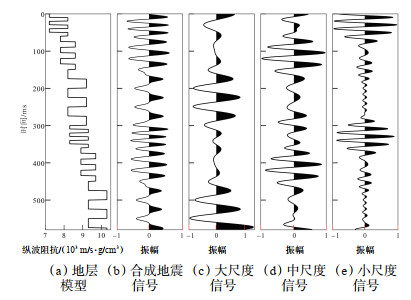
|
下载原图 图 5 多级旋回复合模型不同尺度信号分解结果对比 Fig. 5 Comparison of multi-scale signal decomposition results from the multi-level rotation-coupled model |
地震反演结果的精度很大程度上取决于地震子波构建,不同尺度地震信号的子波特征存在明显差异。大尺度地震统计子波旁瓣能量较弱,统计子波的主频为20 Hz;中尺度信号中提取的地震统计子波旁瓣能量有所增加,其主频为30 Hz;小尺度信号中提取的地震统计子波旁瓣能量较强,其主频约为47 Hz(图 6)。基于以上分析可知,不同尺度地震信号对应的统计子波均与合成信号使用的30 Hz雷克子波存在差异,因此在反演过程中不能直接使用合成信号中的理论子波,需重新从地震信号中提取地震子波 [16]。
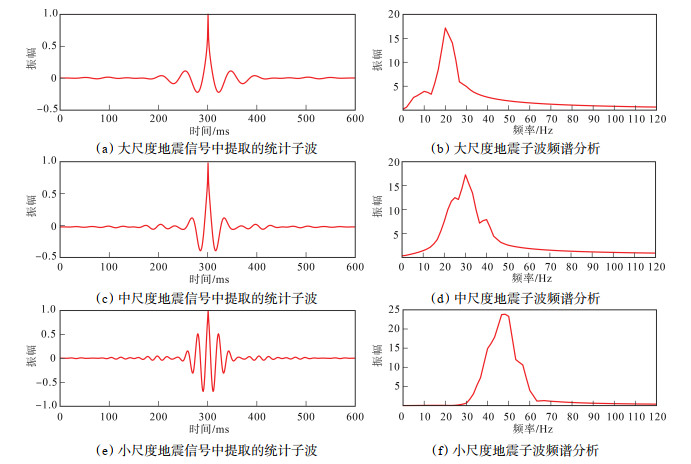
|
下载原图 图 6 不同尺度地震信号中提取的统计子波及其频谱 Fig. 6 Statistical wavelets extracted from seismic signals at different scales and their corresponding frequency spectra |
基于Hamid等 [31]多正则化约束项的权重系数确定思想,联合L曲线法和试错法确定正则化约束项前的权重系数。通常,背景模型约束项的正则化参数过大,会导致反演结果过于平滑,且产生背景模型化,而过小又会导致计算不稳定。当目标函数中包含其他稀疏项时,反演过程不仅依赖背景模型约束项来提升计算的稳定性,还需为背景项设置较小的正则化参数值,进而研究其他2个主导约束项[如式(18-C)中
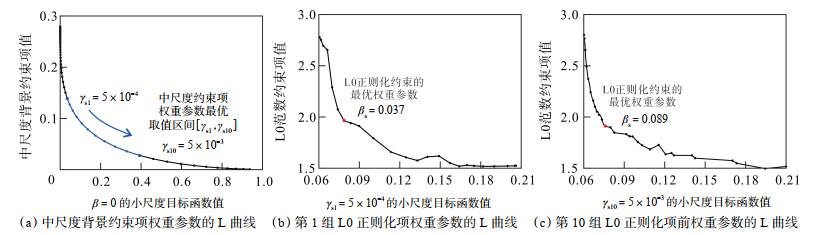
|
下载原图
图 7 正则化参数 |
|
|
下载CSV 表 1 正则化参数测试结果 Table 1 Testing results of regularization parameters |
在大尺度分频信号地震反演中,由于采用的低频模型精度较低,且目标函数约束使用了稀疏性较弱的L2范数,导致反演结果仅能反映模型变化的整体趋势,而无法准确描述薄层与中厚层特征(图 8a)。相比之下,中尺度分频信号的地震反演通过引入稀疏性较强的L1范数,使得反演结果呈现出明显的块状特征,不仅提升了厚层的识别精度,还准确刻画了中频信号中的中厚层特征(图 8b)。小尺度分频信号地震反演采用稀疏性最强且具备较强抗噪性的L0范数进行约束,这种方法能够充分挖掘小尺度信号中的高频信息,如薄层特征(图 8c)。小尺度反演结果是建立在大尺度和中尺度信号反演精度的基础上,因此,地震分频多级稀疏正则化反演结果以小尺度反演结果为准。
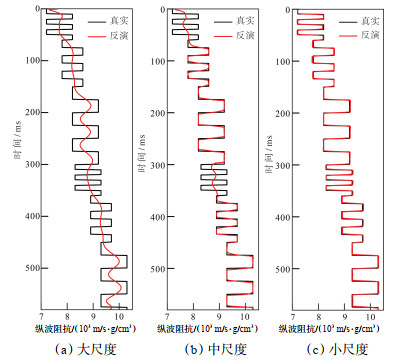
|
下载原图 图 8 多级旋回复合模型不同尺度信号地震反演结果对比 Fig. 8 Comparison of seismic inversion results of different scale signals from the multi-level rotation-coupled model |
稀疏脉冲反演由于其算法具有较强的稳定性,已成为地震储层预测中最常用的反演方法之一。将地震分频多级稀疏正则化反演与稀疏脉冲反演进行对比(图 9),2种方法得到的反演结果趋势基本一致,稀疏脉冲反演稳定性虽好,但分辨能力弱,无法识别薄层信息(如图 9中黑色箭头所示),而地震分频多级稀疏正则化反演结果精度和准确性更高。
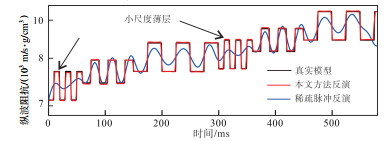
|
下载原图 图 9 多级旋回复合模型稀疏脉冲反演与地震分频多级稀疏正则化反演结果对比 Fig. 9 Comparison of multi-level rotation-coupled sparse pulse inversion and seismic frequency-division multi-level sparse regularization inversion |
以渤中凹陷石臼坨凸起构造带A区为例,验证本文所提出的地震分频多级稀疏正则化反演方法的实用性。A区位于石臼坨凸起南部(图 10a),具有良好的油气运聚条件和巨大的油气勘探潜力,古近系底受北西向和近东西向断裂带控制,新近系以来受北西向和近东西向2组应力控制形成了较复杂的断裂系统 [32-33]。该构造带中潜山为中生界、古生界与太古界形成的大背斜,古近系是一个继承性发育披覆背斜,构造高部位及斜坡区以东营组沉积为主,沙河街组主要分布在边界断层下降盘,受古地貌和沟槽的影响,在古近系形成了以扇三角洲为主的近源沉积体系,古近纪末期的构造抬升使得构造高部位地层剥蚀严重(图 10b)。
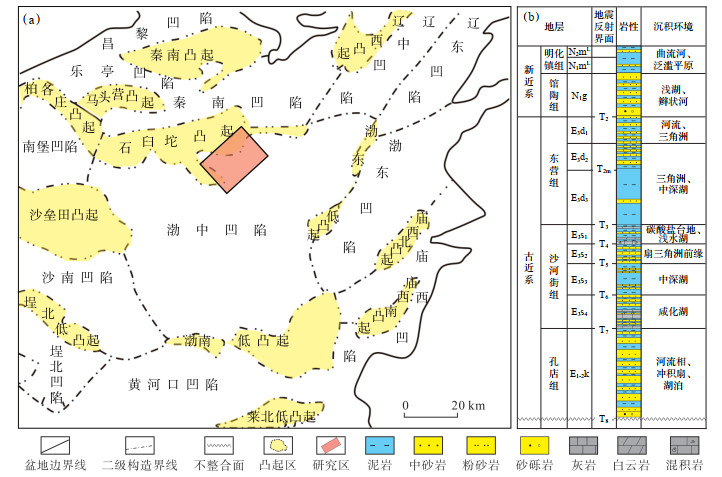
|
下载原图 图 10 渤中凹陷石臼坨凸起构造带位置(a)和古近系岩性地层综合柱状图(b)(据文献[2]修改) Fig. 10 Structural belt location of Shijiutuo Uplift in Bozhong Sag(a)and comprehensive stratigraphic column of Paleogene(b) |
古近系自下而上发育孔店组、沙河街组和东营组,其中东营组可自下而上分为东三段、东二段和东一段,本文主要研究层段东二段可细分为东二上亚段和东二下亚段,其中东二上亚段岩性主要为砂岩以及泥岩,东二下亚段岩性为厚层泥岩与砂岩、粉砂岩互层。东二下亚段与其下伏东三段(主要发育大套厚泥岩层,夹有少量薄层砂岩、粉砂岩)为三角洲和中深湖沉积,泥岩中有机质丰度高、类型好,具有较高生烃潜力。东营组上覆馆陶组沉积了大套泥岩,作为盖层(图 10b)。
研究区东二段对应地震反射层为
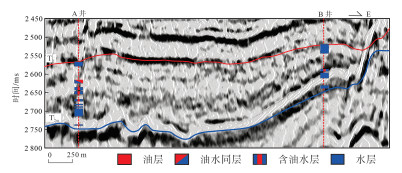
|
下载原图 图 11 渤中凹陷石臼坨凸起A井—B井古近系东营组二段连井地震波形剖面 Fig. 11 Well-tie seismic waveform cross-section of the second member of Paleogene Dongying Formation in well A and well B of Shijiutuo Uplift, Bozhong Sag |
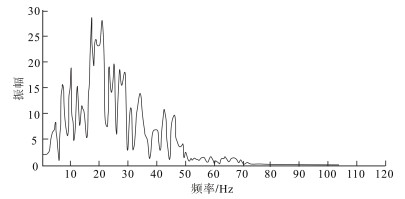
|
下载原图 图 12 渤中凹陷石臼坨凸起古近系东营组二段地震资料频谱 Fig. 12 Spectral analysis of seismic data from the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
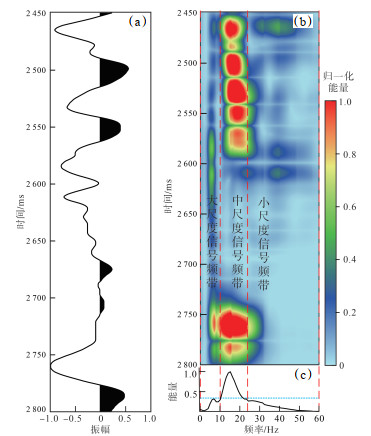
|
下载原图 图 13 渤中凹陷石臼坨凸起A井古近系东营组二段井旁地震道时频谱综合分析 (a)井旁地震道;(b)MP-VWD时频分析;(c)时频能量随频率变化曲线。 Fig. 13 Comprehensive analysis of time-frequency spectrum of seismic traces adjacent to well A in the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
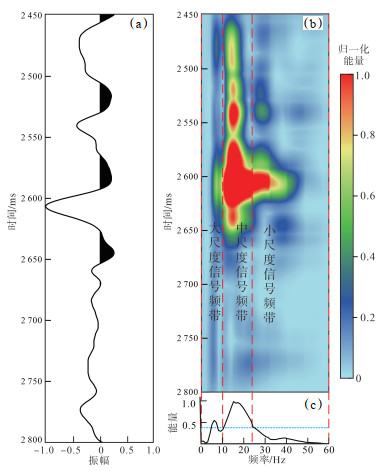
|
下载原图 图 14 渤中凹陷石臼坨凸起B井古近系东二段井旁地震道时频谱综合分析 (a)井旁地震道;(b)MP-VWD时频分析结果;(c)时频能量随频率变化曲线。 Fig. 14 Comprehensive analysis of time-frequency spectrum of seismic traces adjacent to well B in the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
绘制图 11中所有道的时频能量随频率变化曲线,得到二维剖面的时频能量分布(图 15),根据其变化可以将地震信号分为3个尺度,大尺度信号对应频带
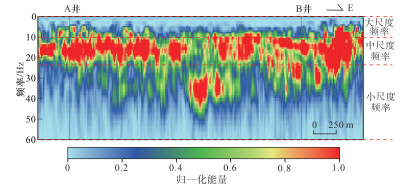
|
下载原图 图 15 渤中凹陷石臼坨凸起A井—B井古近系东二段连井剖面时频能量分布 Fig. 15 Time-frequency energy distribution of crosssection connecting well A and well B in the second member of Paleogene Dongying Formation, Shijiutuo Uplift, Bozhong Sag |
在时频谱能量划分尺度范围内,选取符合频率范围的小波原子,利用MP算法对不同尺度的地震信号进行分频重构,得到地震资料分频结果和统计子波提取结果。结果(图 16)显示:不同尺度地震信号同相轴连续性均较好;与原地震波形剖面(参见图 11)相比,3个尺度的地震波形剖面的信噪比均有所提升;大尺度地震信号的分辨率较低、信噪比较好,小尺度地震信号的分辨率最高,地震资料中强反射轴能量有所压制,弱信号能量得到提升,但弱信号的同相轴连续性较差,存在大量的随机噪音;3个尺度地震信号的统计子波长度均为64 ms,采样间隔均为1 ms。
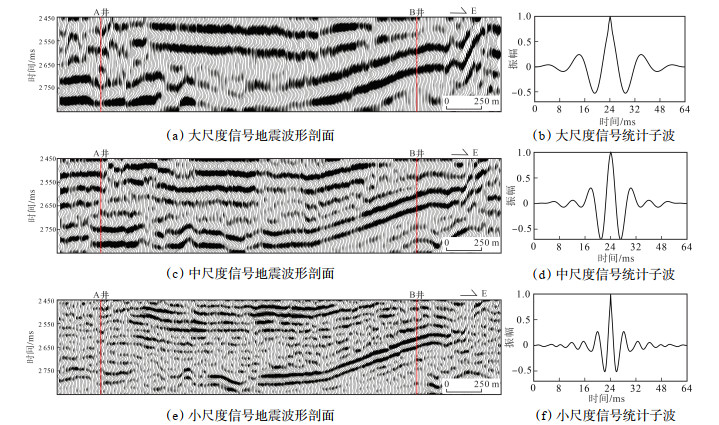
|
下载原图 图 16 渤中凹陷石臼坨凸起古近系东二段A井—B井连井多尺度地震波形剖面及统计子波 Fig. 16 Multi-scale seismic signal waveform cross-section connecting well A and well B and its statistical wavelets in the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
在反演测试中,以B井作为地震反演约束井,A井作为反演验证井。将采用多尺度稀疏约束反演方法得到的大、中、小尺度波阻抗反演结果与单井测井大、中、小尺度的声波阻抗曲线相结合,结果(图 17)显示:不同尺度的反演结果中强波阻抗和弱波阻抗分布位置大致相同;大尺度波阻抗反演结果较稳定可靠,能够较真实地反映砂泥地层波阻抗背景,但仅能刻画地层中的大套砂泥岩体,不能反映中薄层砂体的波阻抗特征;中尺度波阻抗反演结果分辨率有所提升,能够比较明显地刻画储层主体分布;小尺度波阻抗反演结果能够充分利用与挖掘高频信息,精确刻画薄砂体分布特征。将这3个尺度的波阻抗反演结果与A井和B井的对应尺度测井声波阻抗曲线进行对比,井旁波阻抗强度变化与测井曲线变化趋势基本一致,表明不同尺度波阻抗反演结果准确度均较高。A井和B井周围的波阻抗反演体显示出较差的横向连续性,这也说明了石臼坨凸起东二段砂体横向变化快,储层非均质性较强,与现有的工区地质特征认识一致,也证实了地震分频多级稀疏正则化反演方法的可靠性。
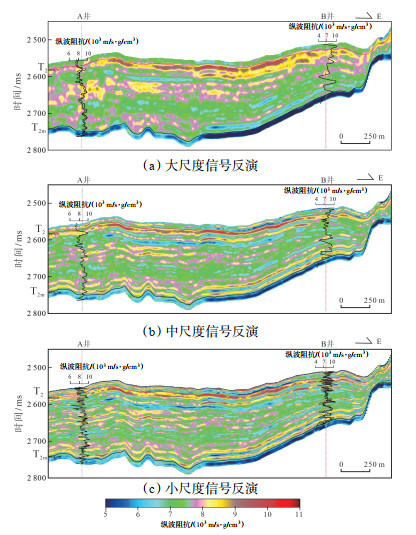
|
下载原图 图 17 渤中凹陷石臼坨凸起A井—B井古近系东营组二段多尺度信号地震反演结果 Fig. 17 Multi-scale seismic inversion results of the cross-section connecting well A and well B in the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
通过地震分频多级稀疏正则化反演得到的A井周围不同尺度的波阻抗结果,与相应尺度的地震波形进行叠合。波阻抗的横向变化特征与对应尺度的地震波形的横向变化特征基本一致(图 18a-18c),进一步验证了该方法在波阻抗反演中始终忠实于地震波形。
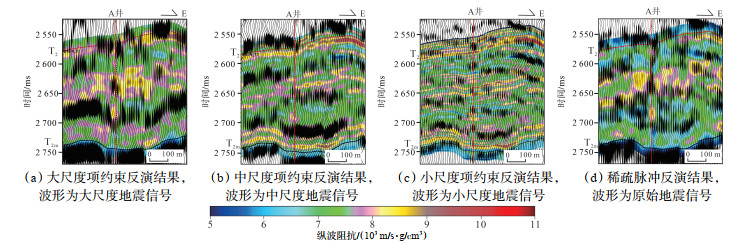
|
下载原图 图 18 渤中凹陷石臼坨凸起A井古近系东二段井旁多尺度反演结果与稀疏脉冲反演结果对比 Fig. 18 Comparison of multi-scale inversion results and sparse pulse inversion results adjacent to well A in the second member of Paleogene Dongying Formation in Shijiutuo Uplift, Bozhong Sag |
对研究区分别进行地震分频多级稀疏正则化反演与稀疏脉冲反演,结果(图 18c,18d)显示:稀疏脉冲反演结果虽能和地震波形变化保持一致,但整体分辨率低,介于地震分频多级稀疏正则化约束的大尺度和中尺度反演结果之间;地震分频多级稀疏正则化反演能够充分挖掘不同尺度信号的频率信息,尤其能够充分利用高频弱信号特征,反演结果具有较高的纵向分辨率,对薄层刻画较准确。
4 结论(1)基于地震分频的多级稀疏正则化反演方法,通过匹配追踪-Wigner-Ville分布技术将地震信号有效分解为大、中、小3个尺度的频段,并在多尺度下应用不同的正则化约束(L2,L1,L0范数),显著提升了薄储层的刻画精度,能够准确挖掘各频段的潜地层特征信息,确保反演结果的可靠信性。
(2)多级稀疏正则化反演方法有效解决了反演过程中不同尺度地震信号的尺度差异问题,通过逐级迭代策略,增强了反演结果的分辨率和抗噪性,单井反演结果与对应的测井声波阻抗曲线吻合度高。
(3)通过渤中凹陷石臼坨凸起构造带A区实际资料应用验证,与传统的稀疏脉冲反演方法相比,地震分频多级稀疏正则化反演对薄储层的识别能力更强,能够准确揭示研究区储层高非均质性和快速横向变化特征。
| [1] |
杨午阳, 魏新建, 李海山. 智能物探技术的过去、现在与未来. 岩性油气藏, 2024, 36(2): 170-188. YANG Wuyang, WEI Xinjian, LI Haishan. The past, present and future of intelligent geophysical technology. Lithologic Reservoirs, 2024, 36(2): 170-188. DOI:10.12108/yxyqc.20240216 |
| [2] |
赵云, 文晓涛, 尹川, 等. 叠前重加权L1范数稀疏约束的地震反演方法. 石油地球物理勘探, 2023, 58(6): 1398-1409. ZHAO Yun, WEN Xiaotao, YIN Chuan, et al. Prestack seismic inversion with reweighted L1-norm sparse constraints. Oil Geophysical Prospecting, 2023, 58(6): 1398-1409. |
| [3] |
罗亚能, 崔京彬, 陈亚军, 等. 改进的地质统计学反演技术[C]//中国石油学会石油物探专业委员会. 第二届中国石油物探学术年会论文集. 涿州: 中国石油东方地球物理公司物探技术研究中心, 2024. LUO Yaneng, CUI Jingbin, CHEN Yajun, et al. Improved geostatistical inversion technique[C]//Petroleum Exploration Committee of China Petroleum Society. Proceedings of the 2nd China petroleum physical prospecting annual conference. Zhuozhou: Physical Exploration Technology Research Center of China Petroleum Oriental Geophysical Company, 2024. |
| [4] |
骆迪, 王宏斌, 蔡峰, 等. 深度学习技术在地震储层预测中的应用及挑战. 石油地球物理勘探, 2024, 59(3): 640-651. LUO Di, WANG Hongbin, CAI Feng, et al. Application and challenges of deep learning technology in seismic data-based reservoir prediction. Oil Geophysical Prospecting, 2024, 59(3): 640-651. |
| [5] |
谢晓军, 吴克强, 张锦伟, 等. 渤中凹陷东南缘东二下亚段扇体成因新认识. 中国海上油气, 2022, 34(3): 28-37. XIE Xiaojun, WU Keqiang, ZHANG Jinwei, et al. A new insight in fan genesis of the lower Ed2 of Dongying Formation in southeastern margin, Bozhong Sag. China Offshore Oil and Gas, 2022, 34(3): 28-37. |
| [6] |
何玉, 周星, 李少轩, 等. 渤海湾盆地渤中凹陷古近系地层超压成因及测井响应特征. 岩性油气藏, 2022, 34(3): 60-69. HE Yu, ZHOU Xing, LI Shaoxuan, et al. Genesis and logging response characteristics of formation overpressure of Paleogene in Bozhong Sag, Bohai Bay Basin. Lithologic Reservoirs, 2022, 34(3): 60-69. DOI:10.12108/yxyqc.20220306 |
| [7] |
JIA Nan, LIU Chiyang, WANG Jianqiang, et al. New insights into Cenozoic evolution of the Shijiutuo uplift, Bohai Bay Basin, China: Constraints from apatite fission track analysis and seismic data. Marine and Petroleum Geology, 2024, 164: 106808. DOI:10.1016/j.marpetgeo.2024.106808 |
| [8] |
徐伟慕, 郭平, 胡天跃. 薄互层调谐与分辨率分析. 石油地球物理勘探, 2013, 48(5): 750-757. XU Weimu, GUO Ping, HU Tianyue. Thin interbed tuning and resolution analysis. Oil Geophysical Prospecting, 2013, 48(5): 750-757. |
| [9] |
成锁, 赵光亮, 王鑫, 等. 基于高分辨率层序约束的薄储层地震预测方法研究. 地球物理学进展, 2024, 39(2): 606-619. CHENG Suo, ZHAO Guangliang, WANG Xin, et al. Thin reservoir seismic prediction method based on high resolution sequence constraint. Progress in Geophysics, 2024, 39(2): 606-619. |
| [10] |
LIU Lei, ZHONG Yijiang, CHEN Hongde, et al. Seismically induced soft-sediment deformation structures in the Palaeogene deposits of the Liaodong Bay Depression in the Bohai Bay Basin and their spatial stratigraphic distribution. Sedimentary Geology, 2016, 342: 78-90. DOI:10.1016/j.sedgeo.2016.06.014 |
| [11] |
CHEN Hehe, ZHU Xiaomin, GAWTHORPE R L, et al. The interactions of volcanism and clastic sedimentation in rift basins: Insights from the Palaeogene-Neogene Shaleitian uplift and surrounding sub-basins, Bohai Bay Basin, China. Basin Research, 2022, 34(3): 1084-1112. DOI:10.1111/bre.12651 |
| [12] |
加东辉, 周心怀, 李建平, 等. 一种少井地区"岩性圈闭表征"的思路: 以辽东湾地区为例. 岩性油气藏, 2009, 21(4): 124-129. JIA Donghui, ZHOU Xinhuai, LI Jianping, et al. A new idea for lithologic trap description with little wells: Taking Liaodongwan area as an example. Lithologic Reservoirs, 2009, 21(4): 124-129. DOI:10.3969/j.issn.1673-8926.2009.04.026 |
| [13] |
YANG Sen, WU Guochen, SHAN Junzhen. Multi-scale seismic envelope inversion method based on sparse representation theory. Journal of Applied Geophysics, 2022, 203: 104685. DOI:10.1016/j.jappgeo.2022.104685 |
| [14] |
赵宝银, 张明. 相控叠前地质统计学反演方法在低渗油藏优质储层预测中的应用: 以A区沙三段3亚段V油组为例. 油气藏评价与开发, 2022, 12(4): 666-676. ZHAO Baoyin, ZHANG Ming. Application of facies-controlled prestack geostatistical inversion method in high quality reservoir prediction of low permeability reservoir: A case study of V Oil Formation of Es33 in Block A. Petroleum Reservoir Evaluation and Development, 2022, 12(4): 666-676. |
| [15] |
桂金咏, 李胜军, 高建虎, 等. 基于特征变量扩展的含气饱和度随机森林预测方法. 岩性油气藏, 2024, 36(2): 65-75. GUI Jinyong, LI Shengjun, GAO Jianhu, et al. A random forests prediction method for gas saturation based on feature variable extension. Lithologic Reservoirs, 2024, 36(2): 65-75. DOI:10.12108/yxyqc.20240207 |
| [16] |
张义, 尹艳树. 约束稀疏脉冲反演在杜坡油田核三段中的应用. 岩性油气藏, 2015, 27(3): 103-107. ZHANG Yi, YIN Yanshu. Application of constrained sparse spike inversion in the third member of Hetaoyuan Formation in Dupo Oilfield. Lithologic Reservoirs, 2015, 27(3): 103-107. DOI:10.3969/j.issn.1673-8926.2015.03.016 |
| [17] |
ALFARRAJ M, ALREGIB G. Semisupervised sequence modeling for elastic impedance inversion. Interpretation, 2019, 7(3): SE237-SE249. DOI:10.1190/INT-2018-0250.1 |
| [18] |
杨爽, 丁建强, 霍晗勇, 等. 基于压缩感知的数据重构技术在拓频处理中的应用. 石油物探, 2023, 62(增刊1): 81-87. YANG Shuang, DING Jianqiang, HUO Hanyong, et al. Application of data reconstruction technology based on compressed sensing in frequency extension processing. Geophysical Prospecting for Petroleum, 2023, 62(Suppl 1): 81-87. |
| [19] |
苏勤, 曾华会, 徐兴荣, 等. 沙漠区地震数据高分辨率处理关键方法及其在尼日尔Agedem地区的应用. 岩性油气藏, 2023, 35(6): 18-28. SU Qin, ZENG Huahui, XU Xingrong, et al. Key techniques of high-resolution processing of desert seismic data and its application in Agedem area, Niger. Lithologic Reservoirs, 2023, 35(6): 18-28. DOI:10.12108/yxyqc.20230603 |
| [20] |
刘文霞. 分频处理技术在辽河深层地震资料处理中的应用. 石油物探, 2001, 40(2): 116-120. LIU Wenxia. Application of frequency divided processing technique in the processing seismic data from the deep-seated formations in Liaohe oil field. Geophysical Prospecting for Petroleum, 2001, 40(2): 116-120. |
| [21] |
胡咏, 于兴河, 胡光义, 等. 印尼C油田储层层序地层分析与沉积相研究. 中国海上油气, 2006, 18(1): 17-21. HU Yong, YU Xinghe, HU Guangyi, et al. Sequence stratigraphy and sedimentary facies of reservoir in C oilfield, Indonesia. China Offshore Oil and Gas, 2006, 18(1): 17-21. |
| [22] |
于建国, 韩文功, 刘力辉. 分频反演方法及应用. 石油地球物理勘探, 2006, 41(2): 193-197. YU Jianguo, HAN Wengong, LIU Lihui. Frequency-divided inversion and application. Oil Geophysical Prospecting, 2006, 41(2): 193-197. |
| [23] |
熊冉, 赵继龙, 厚刚福. 用频谱分解和地震峰值属性分析预测薄砂岩储集层. 新疆石油地质, 2013, 34(2): 225-227. XIONG Ran, ZHAO Jilong, HOU Gangfu. Using spectral decomposition technology and seismic peak attribute analysis for prediction of thin sandstone reservoir. Xinjiang Petroleum Geology, 2013, 34(2): 225-227. |
| [24] |
叶云飞, 刘春成, 刘志斌, 等. 海上宽频地震反演方法及其在南海深水区的应用. 中国海上油气, 2018, 30(2): 65-70. YE Yunfei, LIU Chuncheng, LIU Zhibin, et al. Analysis of marine broadband seismic data inversion and application in deep water of South China Sea. China Offshore Oil and Gas, 2018, 30(2): 65-70. |
| [25] |
代玲, 万钧, 罗泽. 应用波形相控分频反演预测高泥质疏松砂岩薄储层. 物探化探计算技术, 2022, 44(1): 1-8. DAI Ling, WAN Jun, LUO Ze. Application of waveform faciescontrolled frequency division inversion to prediction of thin reservoirs in high-argillaceous unconsolidated sandstone. Computing Techniques for Geophysical and Geochemical Exploration, 2022, 44(1): 1-8. |
| [26] |
李丛, 张栋, 袁青松, 等. 多子波分频反演技术在泥页岩储层预测中的应用研究. 地球物理学进展, 2024, 39(6): 2306-2317. LI Cong, ZHANG Dong, YUAN Qingsong, et al. Application of multi-wavelet frequency division inversion technology in shale reservoir prediction. Progress in Geophysics, 2024, 39(6): 2306-2317. |
| [27] |
XIANG Kun, YANG Yadi, HUANG Handong, et al. Joint impedance inversion and spectral decomposition for deepwater gas reservoir characterization: A case study in South China Sea. Interpretation, 2021, 9(1): T63-T77. |
| [28] |
陈康, 戴隽成, 魏玮, 等. 致密砂岩AVO属性的贝叶斯岩相划分方法: 以川中地区侏罗系沙溪庙组沙一段为例. 岩性油气藏, 2024, 36(5): 111-121. CHEN Kang, DAI Juncheng, WEI Wei, et al. Lithofacies classification of tight sandstone based on Bayesian Facies-AVO attributes: A case study of the first member of Jurassic Shaximiao Formation in central Sichuan Basin. Lithologic Reservoirs, 2024, 36(5): 111-121. DOI:10.12108/yxyqc.20240511 |
| [29] |
SUN Jiajia, LI Yaoguo. Adaptive Lp inversion for simultaneous recovery of both blocky and smooth features in a geophysical model. Geophysical Journal International, 2014, 197(2): 882-899. |
| [30] |
YANG Jun, YIN Cheng, DAI Ronghuo. Seismic impedance inversion via L0 gradient minimisation. Exploration Geophysics, 2019, 50(6): 575-582. |
| [31] |
HAMID H, PIDLISECKY A. Multitrace impedance inversion with lateral constraints. Geophysics, 2015, 80(6): M101-M111. |
| [32] |
张宇焜, 王晖, 胡晓庆, 等. 少井条件下的复杂岩性储层地质建模技术: 以渤海湾盆地石臼坨凸起A油田为例. 石油与天然气地质, 2016, 37(3): 450-456. ZHANG Yukun, WANG Hui, HU Xiaoqing, et al. Reservoir modeling of complex lithologies with sparse wells: A case from a oilfield in Shijiutuo uplift, Bohai Bay Basin. Oil & Gas Geology, 2016, 37(3): 450-456. |
| [33] |
吕世聪, 王少鹏, 张汶, 等. 石臼坨凸起南部陡坡带扇三角洲沉积特征研究. 天然气与石油, 2024, 42(1): 54-62. LYU Shicong, WANG Shaopeng, ZHANG Wen, et al. Research on the sedimentary characteristics of fan delta on the southern steep-slope of Shijiutuo Uplift. Natural Gas and Oil, 2024, 42(1): 54-62. |
 2025, Vol. 37
2025, Vol. 37




