2. 中国石油塔里木油田公司勘探开发研究院, 新疆 库尔勒 841000;
3. 西安三维科技发展有限责任公司, 西安 710021
2. Research Institute of Exploration and Development, Tarim Oilfield Company, PetroChina Tarim Oilfield Company, Korla 84100, Xingjiang, China;
3. Xi'an 3-D Technology Development Co., Ltd., Xi'an 710021, China
油气生产过程中常常会伴随储层应力敏感效应[1-2]及变井筒储集效应[3]。储层应力敏感效应是指储层压力减小引起岩石结构在一定程度上发生变形,进而导致储层渗透率减小的效应[4]。井筒流体发生变井筒储集效应是指关井压力恢复测试时井筒中的油气两相流体因重力差异而发生的相态分离现象,在试井模型建立中,通常用变井筒储集系数模型来考虑变井筒储集效应[5-7]。因此,建立同时考虑储层应力敏感效应和变井筒储集效应的油气两相流试井模型,对试井分析具有重要的理论意义和应用价值。
对应力敏感性储层,Pedrosa[8]早在1986年就提出了渗透率模量概念,即储层的应力敏感效应可以用渗透率与地层压力之间的指数表达式来进行表示。张楠等[9]考虑启动压力梯度和基于岩石本体有效应力理论的应力敏感效应的综合影响,推导出修正的低渗透油藏直井产能方程。李准等[10]通过将直井体积压裂改造后的储层简化为双区径向复合模型,建立了体积压裂直井的瞬态压力计算模型。林永学等[11]对缝洞型碳酸盐岩建立了考虑裂缝应力敏感效应的基质-溶洞-裂缝的三重介质试井解释分析模型。金子一等[12]通过引入拟压力和表皮系数建立了对深层高压应力敏感性碳酸盐岩油藏双重介质试井模型。Zhang等[13]建立了考虑应力敏感效应的油气两相流试井模型。以上考虑应力敏感的试井模型研究主要针对直井井型,而针对水平井井型[14-15],孔垂显等[16]基于双重介质模型,分区(基质-裂缝区、缝网改造区、部分缝网改造区、人工裂缝区)建立了火山岩油藏压裂水平井渗流模型。卢婷等[17]、任宗孝等[18]建立了考虑应力敏感的分段压裂水平井不稳定渗流数学模型。目前,考虑应力敏感效应的试井模型研究较多,但主要聚焦在单相流试井模型研究,且未叠加考虑变井筒储集效应的影响。关于直井井型的油气两相流渗流模型,易劲等[19]基于凝析气渗流的相变特征,建立了凝析油-气两相流方程,并获得拟压力分布解析解;周文武等[20]结合Warren-Root双重介质模型,建立了致密油藏压裂水平井的油气两相流试井模型,并研究了油气两相流对试井曲线的影响;赵立安等[21]采用新型的有限体积IMPES方法,实现了油气两相压力与饱和度的动态模拟。上述研究为深入理解油气两相流的流动特性,为优化试井提供了重要的理论依据和数值分析方法,然而,考虑应力敏感的水平井试井模型相对较少,尤其是油气两相流试井模型更少,对该类井的油气两相流动特征尚不明确,影响后续油井的试井评价及开发。
在综合考虑地层应力敏感效应和变井筒储集效应的基础上,建立水平井油气两相流试井模型,通过模型求解,绘制典型的试井分析理论曲线,并分析各参数的敏感性;通过实例井的试井拟合解释,验证模型的可靠性,为应力敏感性均质储层油气两相流条件下的水平井试井解释提供参考。
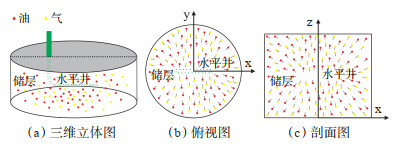
1 物理模型与假设条件水平井油气两相流物理模型主要分为水平井和储层两部分。水平井厚度h、水平渗透率kho、垂向渗透率kve、孔隙度ϕ,水平段长度L,以产量q定产量生产,考虑井筒油气两相密度差异引起的变井筒储集效应和近井地带的储层伤害引起的表皮效应。储层为均质等厚储层,储层流体为油气两相,含气饱和度和含油饱和度分别为Sg和So,遵循等温达西定律;水平井定产量生产前,储层的初始压力为pi,均匀分布;考虑水平面无限大边界条件及储层顶面和底面为不渗透边界条件,储层存在渗透率应力效应,储层渗透率随有效应力呈指数式变化关系。基于此,设置圆柱形平面径向流的储层物理模型,如图 1所示。
|
下载原图 图 1 水平井油气两相流物理模型 Fig. 1 Physical model of oil-gas two-phase flow for horizontal well |
叠加考虑储层应力敏感效应和变井筒储集效应,创建水平井油气两相流的试井模型。数学模型建立的主要步骤如下:
(1)依据压敏性运动方程、状态方程、连续性方程及拟压力定义,推导出用拟压力表示的渗流控制方程;
(2)给出渗流微分方程的定解条件,包括定产量生产及变井筒储集效应的内外边界条件、储层顶底界面条件及水平面外边界条件;
(3)给出模型参数的无因次定义,将数学模型无因次化;
(4)利用正则摄动变换、Fourier变换及Laplace变换对数学模型进行求解,获得Laplace空间下的模型解析解;
(5)利用Stehfest数值反演法将Laplace空间下的解析解反演到真实空间中,获得实际空间下的数值解。
2.2 数学模型 2.2.1 定义变量拟压力函数[13]
| $ m(p)=\int_0^p \frac{k_\mathrm{o}}{\mu_\mathrm{o} B_\mathrm{o}} \mathrm{~d} p $ | (1) |
式中:m为流体拟压力,MPa;p为流体压力,MPa;ko为油相渗透率,D;μο为油相黏度,mPa·s;Вο为油相体积系数,无量纲。
| $ k=k_{\mathrm{i}} e^{-\gamma\left(m_{\mathrm{i}}-m\right)} $ | (2) |
式中:k为绝对渗透率,D;ki为初始绝对渗透率,D;γ为渗透率模量,MPa-1;mi为原始地层拟压力,MPa·D/(mPa·s)。
油相导压系数
| $ \chi_{\mathrm{o}}=\frac{k k_{\mathrm{ro}}}{\phi \mu_{\mathrm{o}} C_{\mathrm{o}}} $ | (3) |
式中:χo为油相导压系数,m2/ks;kro为油相相对渗透率,无量纲;ϕ为孔隙度,无量纲;Сο为原油压缩系数,MPa-1。
气相导压系数
| $ \chi_{\mathrm{g}}=\frac{k k_{\mathrm{rg}}}{\phi \mu_{\mathrm{g}} C_{\mathrm{g}}} $ | (4) |
式中:χg为气相导压系数,cm2/ks;krg为气相相对渗透率,无量纲;μg为气相黏度,mPa·s;Сg为气体压缩系数,MPa-1。
综合导压系数为
| $ \chi_{\text {tol }}=\chi_{\mathrm{o}}+\chi_{\mathrm{g}} $ | (5) |
式中:χtol为综合导压系数,m2/ks。
油气两相流系数为
| $ a=\frac{\sqrt{\chi_{\mathrm{o}} \chi_{\mathrm{g}}}}{\chi_{\text {tol }}} $ | (6) |
式中:a为油气两相流系数。
结合压敏性运动方程、状态方程及连续性方程,基于质量守恒定律,可推导出极坐标下水平井两相流控制方程[12]:
| $ \frac{\partial^2 m}{\partial r^2}+\frac{1}{r} \frac{\partial m}{\partial r}+\gamma\left(\frac{\partial m}{\partial r}\right)^2+\frac{k_{\text {ve }}}{k_{\text {ho }}} \frac{\partial^2 m}{\partial z^2}=\mathrm{e}^{\gamma\left(m_{\mathrm{i}}-m\right)} \frac{1}{\chi_{\text {tol }}} \frac{\partial m}{\partial t} $ | (7) |
式中:r为径向距离,m;kve、kho分别为垂向渗透率、水平渗透率,D;z为垂向距离,m;t为生产时间,h。
2.2.2 定义无因次变量无因次应力敏感系数为
| $ \gamma_{\mathrm{D}}=\frac{q \mu \gamma}{2 {\rm{ \mathsf{ π} }} k h} $ | (8) |
式中:q为流体流量,m3/ks;μ为流体黏度,mPa·s;h为油层厚度,m。
无因次拟压力为
| $ m_{\mathrm{D}}=\frac{2 {\rm{ \mathsf{ π} }} \sqrt{k_{\mathrm{ho}} k_{\mathrm{ve}}} h\left(m_{\mathrm{i}}-m\right)}{q \mu} $ | (9) |
无因次径向半径为
| $ r_{\mathrm{D}}=\frac{r}{r_{\mathrm{w}}} $ | (10) |
式中:rw为井筒半径,m。
无因次生产时间为
| $ t_{\mathrm{D}}=\frac{\sqrt{\chi_{\mathrm{o}} \chi_{\mathrm{g}}}}{\chi_{\mathrm{t}}} \frac{\chi_{\mathrm{t}}}{r_{\mathrm{w}}^2} t $ | (11) |
无因次水平段长度
| $ L_{\mathrm{D}}=\frac{L}{h} \sqrt{\frac{k_{\mathrm{ve}}}{k_{\mathrm{ho}}}} $ | (12) |
式中:L为水平井段的半长,m。
无因次储层厚度为
| $ h_{\mathrm{D}}=\frac{h}{r_{\mathrm{w}}} \sqrt{\frac{k_{\mathrm{ho}}}{k_{\mathrm{ve}}}} $ | (13) |
将上述无因次变量式代入式(7)中,可得到考虑应力敏感的水平井油气两相流无因次控制方程:
| $ \begin{gathered} \frac{\partial^2 m_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2}+\frac{1}{r_{\mathrm{D}}} \frac{\partial m_{\mathrm{D}}}{\partial r_{\mathrm{D}}}+L_D^2 \frac{\partial^2 m_{\mathrm{D}}}{\partial z_{\mathrm{D}}^2}-\gamma_{\mathrm{D}}\left(\frac{\partial m_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right)^2= \\ a\left(h_{\mathrm{D}} L_{\mathrm{D}}\right)^2 \mathrm{e}^{\gamma_{\mathrm{D}} m_{\mathrm{D}}} \frac{\partial m_{\mathrm{D}}}{\partial t_{\mathrm{D}}} \end{gathered} $ | (14) |
式中:zD为无因次垂向距离。
式(14)是非线性方程,为便于求解,引入正则摄动变换[22]:
| $ m_{\mathrm{D}}=-\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right) $ | (15) |
式中:ξD为摄动变换后的无因次压力。
对式(15)求偏微分,可得mD关于rD及tD的偏微分方程:
| $ \frac{\partial m_{\mathrm{D}}}{\partial r_{\mathrm{D}}}=\frac{\partial}{\partial r_{\mathrm{D}}}\left[-\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right)\right]=\frac{1}{\left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right)} \frac{\partial \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}} $ | (16) |
| $ \frac{\partial^2 m_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2}=\frac{\gamma_{\mathrm{D}}}{\left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right)^2}\left(\frac{\partial \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right)^2+\frac{1}{1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}} \frac{\partial^2 \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2} $ | (17) |
| $ \left(\frac{\partial m_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right)^2=\frac{1}{\left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right)^2}\left(\frac{\partial \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right)^2 $ | (18) |
| $ \frac{\partial m_{\mathrm{D}}}{\partial t_{\mathrm{D}}}=-\frac{\partial}{\partial t_{\mathrm{D}}}\left[\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}\right)\right]=\frac{1}{1-\gamma_{\mathrm{D}} \xi_{\mathrm{D}}} \frac{\partial \xi_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ | (19) |
将式(16)(- 19)带入式(15),得:
| $ \frac{\partial^2 \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2}+\frac{1}{r_{\mathrm{D}}} \frac{\partial \xi_{\mathrm{D}}}{\partial r_{\mathrm{D}}}+L_{\mathrm{D}}^2 \frac{\partial^2 \xi_{\mathrm{D}}}{\partial z_{\mathrm{D}}^2}=a\left(h_{\mathrm{D}} L_{\mathrm{D}}\right)^2 \frac{\partial \xi_{\mathrm{D}}}{\partial t_{\mathrm{D}}} $ | (20) |
引入Laplace变换:
| $ L\left[m_{\mathrm{D}}\left(t_{\mathrm{D}}\right)\right]=\bar{m}_{\mathrm{D}}(u)=\int_0^{\infty} m_{\mathrm{D}}\left(t_D\right) \mathrm{e}^{-u t_{\mathrm{D}}} \mathrm{~d} t_{\mathrm{D}} $ | (21) |
式中:u为拉式变量,无量纲。
经Laplace变换后,式(20)变为:
| $ \frac{\partial^2 \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2}+\frac{1}{r_{\mathrm{D}}} \frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}+L_{\mathrm{D}}^2 \frac{\partial^2 \bar{\xi}_{\mathrm{D}}}{\partial z_{\mathrm{D}}^2}=a u\left(h_{\mathrm{D}} L_{\mathrm{D}}\right)^2 \bar{\xi}_{\mathrm{D}} $ | (22) |
式中:ξD为拉式空间下摄动变换后的无因次压力。
考虑定产量生产内边界条件:
| $ \left.\frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right|_{r_{\mathrm{D}}=1}=-\frac{1}{u} $ | (23) |
考虑水平方向无限大外边界条件:
| $ \left.\bar{\xi}_{\mathrm{D}}\right|_{r_{\mathrm{D}} \rightarrow \infty}=0 $ | (24) |
考虑垂向上顶底不渗透边界条件:
| $ \left.\frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial z_{\mathrm{D}}}\right|_{z_{\mathrm{D}}=1}=0 $ | (25) |
| $ \left.\frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial z_{\mathrm{D}}}\right|_{z_{\mathrm{D}}=0}=0 $ | (26) |
引入关于zD的Fourier余弦变换。由Fourier变换与Laplace变换的关系式:
| $ f(t)=L^{-1}[F(s)]=\frac{1}{2 {\rm{ \mathsf{ π} }} j} \int_{\sigma-j \infty}^{\sigma+j \infty} F(s) \mathrm{e}^{s t} \mathrm{~d} s $ | (27) |
式中:s为拉普拉斯变量;j为虚数。
针对ξD采用Fourier逆变换方法,其表达式为
| $ \bar{\xi}_{\mathrm{D}}=\sum\limits_{n=1}^{\infty} \frac{\cos \left(\beta_n z_{\mathrm{D}}\right)}{N(n)} \tilde{\bar{\xi}}_{\mathrm{D}}\left(\beta_n\right) $ | (28) |
| $ \Delta \bar{\xi}=\sum\limits_{n=1}^{\infty} \frac{\cos \left(\beta_n z_{\mathrm{D}}\right)}{N(n)} \Delta \tilde{\bar{\xi}}\left(\beta_n\right) $ | (29) |
式中:n为频率分量的序号,无量纲;Δ为频率集散点之间的间隔。
N(n)为傅里叶级数,表达式为
| $ N(n)=\int_0^1\left(\cos \beta_n z_{\mathrm{D}}\right)^2 d z_{\mathrm{D}}=\left\{\begin{array}{l} \frac{1}{2}(n>0) \\ 1(n=0) \end{array}\right. $ | (30) |
βn为特征值,由下式确定:
| $ \sin \left(\beta_n\right)=0, \beta_n=n {\rm{ \mathsf{ π} }} $ | (31) |
针对控制方程和内边界条件作关于zD的Fourier余弦变换:
| $ \frac{\partial^2 \tilde{\bar{\xi}}_{\mathrm{D}}}{\partial r_{\mathrm{D}}^2}+\frac{1}{r_{\mathrm{D}}} \frac{\partial \tilde{\bar{\xi}}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}-L_{\mathrm{D}}^2 \beta_n^2 \tilde{\bar{\xi}}_{\mathrm{D}}=a u \tilde{\bar{\xi}}_{\mathrm{D}} $ | (32) |
| $ \left.r_{\mathrm{D}} \frac{\partial \tilde{\bar{\xi}}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right|_{r_{\mathrm{D}} \rightarrow 0}=-\frac{1}{2 u} \cos n {\rm{ \mathsf{ π} }} z_{\mathrm{wD}} $ | (33) |
式中:zwD为无因次井筒位置处的垂向距离。
对控制方程移项得到:
| $ \frac{\partial^2 \tilde{\bar{\xi}}_{\mathrm{D}}}{\partial r_{\mathrm{D}}{ }^2}+\frac{1}{r_{\mathrm{D}}} \frac{\partial \tilde{\bar{\xi}}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}-\left(L_{\mathrm{D}}{ }^2 \beta_n{ }^2+a u\right) \tilde{\bar{\xi}}_{\mathrm{D}}=0 $ | (34) |
上述为Bessel方程,其通解为:
| $ y=A K_0(x)+B I_0(x) $ | (35) |
微分方程通解为:
| $ \tilde{\bar{\xi}}_{\mathrm{D}}=A \mathrm{~K}_0\left(\sqrt{L_{\mathrm{D}}{}^2 \beta_n{}^2+a u} r_{\mathrm{D}}\right)+B \mathrm{I}_0\left(\sqrt{L_{\mathrm{D}}{}^2 \beta_n{}^2+a u} r_{\mathrm{D}}\right) $ | (36) |
令
| $ \bar{\xi}_{\mathrm{D}}=A_1 \mathrm{~K}_0\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)+A_2 \mathrm{I}_0\left(\sqrt{\tau_n} r_{\mathrm{D}}\right) $ | (37) |
| $ \frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}=-A_1 T \mathrm{K}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)+A_2 T \mathrm{I}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right) $ | (38) |
式中:K0、K1分别为零阶贝塞尔K函数和一阶贝塞尔K函数;I0、I1分别为零阶贝塞尔I函数和一阶贝塞尔I函数;A1、A2为待定系数。
将边界条件代入微分方程通解后求取A1、A2的值。
对于无限大边界,由Bessel函数性质可知:
| $ \lim\limits_{r_0 \rightarrow \infty} I_0(x) \rightarrow \infty $ | (39) |
因此,A2 = 0,压力通解可写作:
| $ \bar{\xi}_{\mathrm{D}}=A_1 \mathrm{K}_0\left(\sqrt{\tau_n} r_{\mathrm{D}}\right) $ | (40) |
| $ \frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}=-A_1 T \mathrm{K}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right) $ | (41) |
将内边界条件式(26)代入式(41),压力通解可写作:
| $ \left.\frac{\partial \bar{\xi}_{\mathrm{D}}}{\partial r_{\mathrm{D}}}\right|_{r_{\mathrm{D}}=1} =-A_1 T \mathrm{K}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)=-\frac{1}{2 u} $ | (42) |
| $ A_1 =\frac{1}{2 u T \mathrm{K}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)} $ | (43) |
将A1、A2的值代入式(37),可以得到无限大边界油气两相流压力通解为:
| $ \bar{\xi}_{\mathrm{D}}=\frac{\mathrm{K}_0\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)}{2 u T \mathrm{K}_1\left(\sqrt{\tau_n} r_{\mathrm{D}}\right)} $ | (44) |
油气井在实际生产过程中,由于井筒中的重力滑脱作用或是井底积液等原因,会产生变井储效应。对于此种情况,使用Hegeman变井储模型[23]以及Duhamel原理。
Duhamel原理的表达式为:
| $ \bar{\xi}_{\mathrm{wD} 0}=\frac{\left(u \bar{\xi}_{\mathrm{wD}}+S\right)\left(1+C_{\mathrm{D}} u^2 \bar{\xi}_{\phi \mathrm{D}}\right)}{u+C_{\mathrm{D}} u^2\left(u \bar{\xi}_{\mathrm{wD}}+S\right)} $ | (45) |
式中:S为表皮系数,无量纲;CD为无因次井筒储集系数;ξwD为不考虑井筒储集效应和表皮效应的无因次摄动变换后的井底压力;ξϕD为考虑变井筒储集效应的无因次摄动变换后的井底压力;ξwD0为考虑了变井筒储集效应和表皮效应的无因次摄动变换后的井底压力。
Hegeman变井储模型表达式如下:
| $ \bar{\xi}_{\phi \mathrm{D}}=C_{\phi \mathrm{D}} \operatorname{erf}\left(\frac{t_{\mathrm{D}}}{\alpha_{\mathrm{D}}}\right) $ | (46) |
式中:CϕD为与压力相关的无因次变井储系数。
| $ C_{\phi \mathrm{D}}=\frac{k h C_\phi}{q B_{\mathrm{f}} \mu} $ | (47) |
式中:Cϕ为与压力相关的变井储系数,MPa;Bf为流体的体积系数,无量纲。
αD为与时间相关的无因次变井储系数:
| $ \alpha_{\mathrm{D}}=\frac{\alpha \chi_{\mathrm{t}}}{r_{\mathrm{w}}{ }^2} $ | (48) |
对模型在拉式空间下的井底压力通解进行Stehfest数值反演,从而可以得到真实空间下的无因次摄动变换后的井底拟压力ξwD0,然后使用正则摄动变换得到考虑应力敏感效应的无因次油气两相流井底拟压力(mwD)通解:
| $ m_{\mathrm{wD}}=-\frac{1}{\gamma_{\mathrm{D}}} \ln \left(1-\gamma_{\mathrm{D}} \bar{\xi}_{\mathrm{wD} 0}\right) $ | (49) |
令mwD'为无因次拟压力导数:
| $ m_{\mathrm{wD}}^{\prime}=\frac{\mathrm{d} m_{\mathrm{wD}}}{\mathrm{~d}\left(t_{\mathrm{D}} / C_{\mathrm{D}}\right)} $ | (50) |
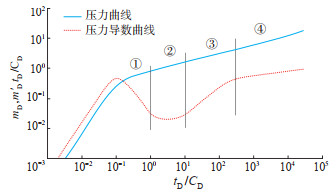
设置水平井油气两相流物理模型参数(表 1),并绘制考虑应力敏感的水平井油气两相流试井理论曲线,以tD/CD为横坐标(tD为无因次生产时间;CD为无因次井筒储集系数);以mD,mD'tD/CD为纵坐标(mwD为无因次拟压力,mwD'为无因次拟压力导数)。结果(图 2)显示:曲线上可识别4个主要的流动阶段,第①阶段为变井储和表皮效应影响段,与定井储效应的早期压力和压力导数曲线重合且呈单位斜率的直线特征[24]不同,受变井储的影响,早期压力和压力导数曲线呈分离状态,受表皮效应的影响,压力导数曲线呈“驼峰”状;第②阶段,早期径向流阶段;第③阶段,水平井线性流阶段;第④阶段,晚期拟径向流阶段。
|
|
下载CSV 表 1 水平井油气两相流物理模型相关参数 Table 1 Physical model parameters of oil-gas two-phase flow for horizontal well |
|
下载原图 图 2 考虑应力敏感的水平井油气两相流物理模型试井理论曲线 Fig. 2 Well testing theory curves of physical model of oil-gas two-phase flow for horizontal well in consideration of stress sensitivity |
通过改变某一模型参数的取值,维持其他模型参数不变,可绘制不同参数取值条件下的试井理论曲线,进而分析试井曲线对该模型参数的敏感性。
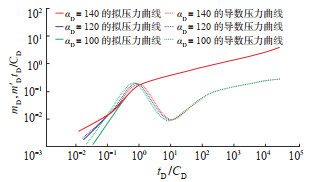
3.2.1 无因次变井储系数αD和CϕD维持LD = 6,γD = 0.06,CϕD = -3,So = 10% 不变,依次设置αD值分别为100,120和140,分别绘制试井曲线,分析αD的敏感性。结果(图 3)显示,αD越大,其压力导数曲线的“驼峰”越靠右,指示变井储效应持续的时间就越长。
|
下载原图 图 3 水平井油气两相流物理模型中与时间有关的无因次变井储系数αD的敏感性分析曲线 Fig. 3 Sensitivity analysis of αD in the physical model of oil-gas two-phase flow of horizontal well |
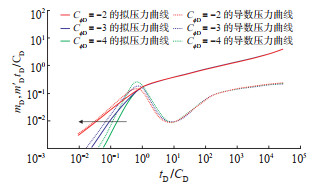
维持LD =6,γD = 0.06,αD = 100,So = 10% 不变,依次设置CϕD值为100,120和140,分别绘制试井曲线。结果(图 4)显示:CϕD越小,其压力导数曲线的“驼峰”位置就越高。
|
下载原图 图 4 水平井油气两相流物理模型中与压力有关的无因次变井储系数CϕD的敏感性分析曲线 Fig. 4 Sensitivity analysis of CϕD in physical model of oil-gas two-phase flow of horizontal well |
综上分析可知,在表皮效应阶段,井筒储集效应并未完全结束,故αD和CϕD值的变化主要影响井筒流动阶段、表皮效应阶段的试井曲线形态及位置,对后期基质渗流贡献阶段的试井曲线形态无影响。
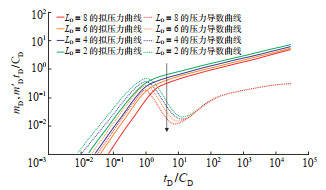
3.2.2 无因次水平井长度LD维持CϕD = -3,γD = 0.06,αD = 100,So = 10% 不变,依次设置LD值为2,4,6和8,分别绘制试井曲线。结果(图 5)显示:相同产量、相同生产时间条件下,LD越大,压力降落幅度越小,试井压力曲线位置越低,指示泄流面积越大,地层供给能力越强,主要影响第②阶段和第③阶段。
|
下载原图 图 5 水平井油气两相流物理模型中无因次水平井长度LD的敏感性分析曲线 Fig. 5 Sensitivity analysis of LD in physical model of oil-gas two-phase flow of horizontal well |
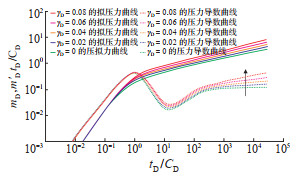
维持LD =6,CϕD = -3,αD = 100,So = 10% 不变,依次设置γD值为0.02,0.04,0.06和0.08,分别绘制试井曲线。结果(图 6)显示:γD影响除早期井筒储集效应阶段之外的试井曲线形态;相同生产时间条件下,γD越大,压力降落幅度越大,试井压力曲线位置越高,试井压力导数曲线末段上翘越明显,说明其应力敏感效应越明显,渗透率下降幅度越大,渗流阻力越大;γD对试井曲线形态的影响,随时间的增加而增大,当γD等于0时,模型为常规不考虑应力敏感效应的试井模型,试井压力导数曲线末段变为水平线。
|
下载原图 图 6 水平井油气两相流物理模型中无因次应力敏感系数γD的敏感性分析曲线 Fig. 6 Sensitivity analysis of γD in physical model of oil-gas two-phase flow of horizontal well |
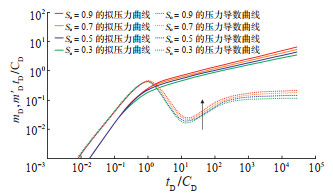
维持LD =6,CϕD = -3,γD = 0.06,αD = 100不变,依次设置So值为30%,50%,70% 和90%,分别绘制试井曲线。结果(图 7)显示:相同生产时间条件下,So越大,压力降落幅度越大,试井压力曲线位置越高,说明So越大,原油流动能力弱于气体的流动能力,油气两相流流动阻力越大。
|
下载原图 图 7 水平井油气两相流物理模型中含油饱和度So的敏感性分析曲线 Fig. 7 Sensitivity analysis of So in physical model of oil-gas two-phase flow of horizontal well |
新疆XXX-H水平井,于2016年1月投产,原始地层压力为86.67 MPa,泡点压力为47.33 MPa,截止2024年10月,地层压力为44.82 MPa,地层处于油气两相流阶段。该井以8 mm油嘴稳定生产,平均日产油量264 t、日产气量29.66×104 m3,气油比为2 289 m3/t,日产气、油量相对稳定。2024年10月,该井开展过压力恢复试井测试,关井测试时间为228 h,关井前8 mm油嘴稳定生产时间为496 h。基础数据(表 2)。
|
|
下载CSV 表 2 新疆XXX-H井试井解释基础数据 Table 2 Basic data of well testing interpretation of well XXX-H in Xinjiang |
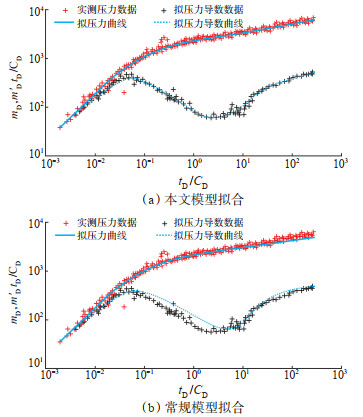
分别采用考虑应力敏感的水平井油气两相流试井模型(本文设计模型)、不考虑应力敏感效应的常规水平井单相渗流模型对新疆XXX-H井开展压力恢复试井解释,模型拟合的双对数曲线与实测数据的双对数曲线的吻合程度较高(图 8a),根据该模型的解释结果,该井试油解释结果(表 3)。常规模型在早期径向流阶段和晚期径向流阶段的试井测试数据拟合效果差(图 8b)。
|
下载原图 图 8 新疆XXX-H井试井解释曲线拟合图 Fig. 8 Fitting curves of well testing interpretations of well XXX-H in Xinjiang |
|
|
下载CSV 表 3 新疆XXX-H井试井解释结果数据 Table 3 Results of well testing interpretation of well XXX-H in Xinjiang |
(1)考虑应力敏感的水平井油气两相流模型在新疆某水平井中拟合的压力曲线、压力导数曲线与实测压力数据的吻合程度高,该模型可靠。
(2)考虑应力敏感性水平井油气两相流渗流样版曲线反映出4个主要的流动阶段,分别为变井储和表皮效应影响段、早期径向流阶段、水平井线性流阶段及晚期拟径向流阶段。
(3)考虑应力敏感的水平井油气两相流试井理论曲线显示:变井储系数主要影响井筒流动阶段和表皮效应阶段;无因次水平井长度越大,早期径向流和中期线性流阶段的无因次拟压力及拟压力导数曲线位置越低;无因次应力敏感系数影响除早期井筒储集效应阶段之外的试井曲线形态,无因次应力敏感系数越大,渗流通道变形越明显,流体需要克服在地层中的流动阻力越大,无因次拟压力及拟压力导数曲线位置越高;当出现两相流时,随着油相饱和度增大,整体流动阻力增大,井储和表皮驼峰效应越明显。
| [1] |
苏皓, 郭艳东, 曹立迎, 等. 顺北油田断控缝洞型凝析气藏衰竭式开采特征及保压开采对策. 岩性油气藏, 2024, 36(5): 178-188. SU Hao, GUO Yandong, CAO Liying, et al. Natural depletion characteristics and pressure maintenance strategies of fault controlled fracture-cavity condensate gas reservoirs in Shunbei Oil-field. Lithologic Reservoirs, 2024, 36(5): 178-188. DOI:10.12108/yxyqc.20240517 |
| [2] |
史英, 颜菲, 李小波, 等. 考虑应力敏感疏松砂岩气藏试井分析. 岩性油气藏, 2009, 21(3): 114-117. SHI Ying, YAN Fei, LI Xiaobo, et al. Well test analysis of unconsolidated sandstone gas reservoir in consideration of stress sensitivity. Lithologic Reservoirs, 2009, 21(3): 114-117. DOI:10.3969/j.issn.1673-8926.2009.03.025 |
| [3] |
贾永禄, 李允, 邓吉彬. 具有井筒相分离和层间窜流的层状油藏渗流井底压力精确解. 西南石油学院学报, 1997, 19(1): 40-44. JIA Yonglu, LI Yun, DENG Jibin. Analytical solution of bottom hole pressure behavior in layered reservoirs with wellbore phase redistribution and crossflow. Journal of Southwest Petroleum Institute, 1997, 19(1): 40-44. |
| [4] |
李传亮, 朱苏阳. 关于应力敏感测试方法的认识误区. 岩性油气藏, 2015, 27(6): 1-4. LI Chuanliang, ZHU Suyang. Misunderstanding of measuring methods of stress sensibility. Lithologic Reservoirs, 2015, 27(6): 1-4. DOI:10.3969/j.issn.1673-8926.2015.06.001 |
| [5] |
FAIR W B. Pressure buildup analysis with wellbore phase redistribution. SPE Journal, 1981, 21(2): 259-270. |
| [6] |
陈艳芳, 赵宏军. 低渗气藏变井储试井分析研究. 油气井测试, 2017, 26(3): 33-35. CHEN Yanfang, ZHAO Hongjun. Well testing analysis and research on variable wellbore storage in low permeability gas reservoir. Well Testing, 2017, 26(3): 33-35. |
| [7] |
杨洪志, 冯文光, 陈友莲. 考虑井筒相分离的污染检测试井研究及应用. 成都理工学院学报, 2000, 27(2): 137-140. YANG Hongzhi, FENG Wenguang, CHEN Youlian. A study on damage test with wellbore phase redistribution and its application. Journal of Chengdu University of Technology, 2000, 27(2): 137-140. |
| [8] |
PEDROSA O A. Pressure transient response in stress-sensitive formations[R]. Oakland, The SPE California Regional Meeting, 1986.
|
| [9] |
张楠, 王晓琴, 徐锋, 等. 启动压力梯度和应力敏感效应对低渗透油藏直井产能的影响. 特种油气藏, 2012, 19(1): 74-77. ZHANG Nan, WANG Xiaoqin, XU Feng, et al. Effects of kickoff pressure gradient and stress sensitivity on the productivity of vertical wells in low permeability reservoirs. Special Oil & Gas Reservoirs, 2012, 19(1): 74-77. DOI:10.3969/j.issn.1006-6535.2012.01.017 |
| [10] |
李准, 吴晓东, 任允鹏, 等. 致密储层体积压裂直井瞬态压力计算模型. 大庆石油地质与开发, 2019, 38(4): 152-159. LI Zhun, WU Xiaodong, REN Yunpeng, et al. Calculating model of the transient pressure for the volume-fractured vertical well in tight reservoirs. Petroleum Geology & Oilfield Development in Daqing, 2019, 38(4): 152-159. |
| [11] |
林永学, 高书阳, 曹耐, 等. 考虑应力敏感的缝洞型油藏三重介质试井分析理论模型. 科学技术与工程, 2021, 21(11): 4345-4351. LIN Yongxue, GAO Shuyang, CAO Nai, et al. A theoretical model of triple medium well test analysis for fractured-vuggy reservoirs considering stress sensitivity. Science Technology and Engineering, 2021, 21(11): 4345-4351. |
| [12] |
金子一, 贾品, 程林松, 等. 深层高产碳酸盐岩油藏试井解释模型及其应用. 陕西科技大学学报, 2022, 40(6): 108-115. JIN Ziyi, JIA Pin, CHENG Linsong, et al. Well test model and its application in deep high-yield carbonate reservoir. Journal of Shaanxi University of Science & Technology, 2022, 40(6): 108-115. |
| [13] |
ZHANG Chunyu, CHEN Shijia, ZHU Songbai, et al. Modelling pressure dynamics of oil-gas two-phase flow in double-porosity media formation with permeability-stress sensitivity. Scientific Reports, 2024, 14(1): 24418. DOI:10.1038/s41598-024-71493-1 |
| [14] |
姜瑞忠, 张春光, 郜益华, 等. 缝洞型碳酸盐岩油藏水平井分形非线性渗流. 岩性油气藏, 2019, 31(6): 118-126. JIANG Ruizhong, ZHANG Chunguang, GAO Yihua, et al. Fractal nonlinear seepage model of horizontal wells in fracturedvuggy carbonate reservoirs. Lithologic Reservoirs, 2019, 31(6): 118-126. DOI:10.12108/yxyqc.20190613 |
| [15] |
LIU Hailong. Dynamic analysis of bottom hole pressure of a horizontal well in fracture-cavity reservoirs. Environmental Earth Sciences, 2022, 81(10): 1-17. |
| [16] |
孔垂显, 巴忠臣, 崔志松, 等. 火山岩油藏压裂水平井应力敏感产能模型. 岩性油气藏, 2021, 33(4): 166-175. KONG Chuixian, BA Zhongchen, CUI Zhisong, et al. Stresssensitive productivity model of fractured horizontal wells in volcanic reservoirs. Lithologic Reservoirs, 2021, 33(4): 166-175. DOI:10.12108/yxyqc.20210418 |
| [17] |
卢婷, 王鸣川, 马文礼, 等. 考虑多重应力敏感效应的页岩气藏压裂水平井试井模型. 新疆石油地质, 2021, 42(6): 741-748. LU Ting, WANG Mingchuan, MA Wenli, et al. Fractured horizontal well test model for shale gas reservoirs with considering multiple stress sensitive factors. Xinjiang Petroleum Geology, 2021, 42(6): 741-748. |
| [18] |
任宗孝, 李旭飞, 蒋海岩, 等. 考虑应力敏感的低渗透油藏分段压裂水平井三维不稳定渗流模型. 中国科技论文, 2023, 18(1): 10-16. REN Zongxiao, LI Xufei, JIANG Haiyan, et al. Three-dimensional unsteady flow model of multistage fractured horizontal well in low permeability reservoir considering stress sensitivity. China Science Paper, 2023, 18(1): 10-16. |
| [19] |
易劲, 贾永禄, 赵海洋, 等. 凝析气藏水平井井底压力动态分析. 断块油气田, 2008, 15(2): 54-57. YI Jin, JIA Yonglu, ZHAO Haiyang, et al. Performance analysis of bottom-hole pressure for horizontal well in condensate gas reservoir. Fault-Block Oil & Gas Field, 2008, 15(2): 54-57. |
| [20] |
周文武, 李勇明, 郑杰, 等. 致密油藏压裂水平井油气两相流试井模型研究与分析. 油气藏评价与开发, 2017, 7(5): 38-43. ZHOU Wenwu, LI Yongming, ZHENG Jie, et al. Oil-gas twophase flow well test model analysis of fractured horizontal wells in tight oil reservoir. Petroleum Reservoir Evaluation and Development, 2017, 7(5): 38-43. |
| [21] |
赵立安, 史乐, 钟彩霞, 等. 新型油气两相有限体积IMPES数值试井模型算法. 西安石油大学学报(自然科学版), 2020, 35(5): 60-64. ZHAO Li'an, SHI Le, ZHONG Caixia, et al. A finite volume IMPES algorithm for numerical well testing of oil-gas twophase flow. Journal of Xi'an Shiyou University(Natural Science Edition), 2020, 35(5): 60-64. |
| [22] |
朱经浩, 陈硕晶. Gurman摄动变换在非凸全局优化中的应用. 同济大学学报(自然科学版), 2013, 41(5): 788-791. ZHU Jinghao, CHEN Shuojing. Non-convex global optimization with Gurman perturbation. Journal of Tongji University (Natural Science), 2013, 41(5): 788-791. |
| [23] |
HEGEMAN P S, HALLFORD D L, JOSEPH J A. Well-test analysis with changing wellbore storage. SPE Formation Evaluation, 1993, 8(3): 201-207. DOI:10.2118/21829-PA |
| [24] |
陈艳芳, 赵宏军. 低渗气藏变井储试井分析研究. 油气井测试, 2017, 26(3): 33-35. CHEN Yanfang, ZHAO Hongjun. Well testing analysis and research on variable wellbore storage in low permeability gas reservoir. Well Testing, 2017, 26(3): 33-35. |
 2025, Vol. 37
2025, Vol. 37



