2. 中国石油大学(华东) 储运与建筑工程学院,山东 青岛 266580
2. College of Pipeline and Civil Engineering, China University of Petroleum(East China), Qingdao 266580, Shandong, China
干热岩作为清洁能源中的一种,具有储量大、范围广、绿色低碳环保等一系列特征[1],对降低由化石能源燃烧造成二氧化碳(CO2)过量排放引起的全球气候问题具有重要意义[2-4]。现阶段,干热岩开发通常采用增强型地热系统(Enhanced Geothermal Systems,简称EGS)[5],而在EGS系统中,采热工质对于取热效率至关重要。考虑到超临界CO2相对于水在黏度、热虹吸、载热能力等方面的优势[6-7],可以采用超临界CO2取代水作为EGS系统中的采热工质,即CO2-EGS[8]。此举既可以解决干热岩热储的高效取热难题,又可以实现CO2地质封存减缓温室效应[9-11],且已被相关文献理论验证[12-13]。然而,目前关于CO2-EGS的研究处于初始阶段,尚未进入商业化阶段,实际生产数据较少,难以形成统一的认识和结论,因此亟需从数值模拟角度开展CO2- EGS干热岩热储开发研究。
在干热岩热储开发数值模拟方面,多物理场耦合是必须考虑的问题,即温度场、渗流场、应力场的相互作用(THM作用)。针对干热岩热储开发THM耦合模型方面,已有学者取得了一系列成果,Ghassemi等[14]以单条裂隙为研究对象,建立了干热岩开发THM耦合模型,结果表明在运行初期,裂隙变形行为受孔隙流体压力的影响为主,而在运行后期,裂隙变形行为受温度变化的影响为主。Koh等[15]考虑二维随机裂隙分布影响建立了干热岩热储THM耦合模型,结果表明干热岩随机裂缝渗透率受岩体温度变化引起的热应力长期影响,造成干热岩热储温度分布以及产出液温度的变化。Jing等[16]考虑三维随机裂隙分布规律,建立了干热岩热储THM耦合模型,并特别讨论了应力场对干热岩开发的影响机制,结果发现注入流体与干热岩热储的温差将增大热储渗透率,进而增大注入量和产出液质量。曹文炅等[17]考虑非热平衡假设和THM耦合作用,基于三维概化模型提出了干热岩热储开发数值模型,结果表明干热岩热储应力场、渗流场和温度场耦合作用在注入井附近更为强烈,同时应力场变化对干热岩开发效果也造成了一定影响。Hicks等[18]考虑裂缝随机分布影响,建立了水作为采热工质的干热岩热储EGS开发THM耦合模型,揭示了仅考虑热流两场耦合将过高估计产出液温度。Taron等[19-20]考虑随机裂缝影响,提出了干热岩热储开发的THM耦合模型,获取了应力场对采热性能的影响主要集中在中短期。MeDermott等[21]基于数值模拟认为,干热岩热储内生产井附近裂缝区域的快速降温,导致岩体收缩变形增大裂缝渗透率,加剧采热工质流动的集中性,引起热突破时间提前,对采热性能和换热效率产生不利影响。Sun等[22]考虑了地下水流方程和多孔介质传热方程的耦合,建立了直井开发的EGS数值模型,比较了一注多采与一注两采模式之间的传热性能差异,结果表明一注多采的寿命明显长于相应的一注两采,且一注多采的发热量多于一注两采。
现有模型已取得了丰富的成果,但仍然存在不足: ①现有THM耦合模型主要以水作为采热工质展开研究,对于干热岩CO2-EGS开发的THM耦合数值模拟较少,尚未形成统一的认识和看法; ②现阶段的研究大多集中在直井开发,采用水平井多簇压裂改造热储的CO2-EGS干热岩开发尚未报道,特别是水平井井网参数和多簇压裂缝网参数对采热能力的影响尚未讨论。基于此,通过修改孔隙度和渗透率函数表达式,建立了多簇压裂裂缝条件下CO2-EGS干热岩水平井开发THM耦合模型,讨论了THM耦合作用、水平井井网参数、多簇压裂缝网参数等对干热岩CO2-EGS采热性能的影响规律。本次提出的多簇压裂裂缝热-流-固耦合模型,提供了理论上对CO2-EGS系统优化的关键参数,并在实际开发中具有重要的意义,尤其是在提高热交换效率方面。
1 CO2-EGS的THM耦合数学模型通过CO2-EGS实现干热岩热储水平井开发时,干热岩热储为包含基质和多簇压裂缝网的双重介质模型,其中,基质是超低渗的孔隙介质,多簇压裂缝网是超临界CO2的主要流动通道,渗透率相对基质较高,但仍属于低渗范畴。另外,在建立CO2- EGS的THM耦合数学模型时,应满足以下假设[23]: ①干热岩热储内部不含水; ②流体流动符合达西定律; ③多簇压裂缝网内的流体换热方式为强制对流和热传导; ④岩体变形满足Biot固结理论和有效应力原理。
1.1 基质控制方程(1) 基岩应力场方程
| $ \sigma_{i j, j}+F_i=0 $ | (1) |
| $ \mu u_{i, i j}+(\lambda+\mu) u_{j, i j}-\alpha_{\mathrm{B}} p_{, i}-\beta_{\mathrm{T}} T_{\mathrm{s}, i}+F_i=0 $ | (2) |
其中: μ = E/2(1 + υ),λ = Eυ/[(1 + υ)(1-2υ)],βT = αTE/(1 - 2υ)。
式中: σij,j为应力二阶张量分量,Pa,下标i,j为笛卡尔坐标系分量指标(i,j = 1,2,3,对应x,y,z方向),i为应力作用面的法线方向; j为应力分量的作用方向; u为位移,m; Fi为体力,Pa; λ与μ为拉梅常数; E为弹性模量,Pa; p为流体压力,Pa; αB为Biot固结系数; Ts为基质温度,K; βT为热膨胀因子; αT为热膨胀系数,1/K; αB p,i为流体压力作用项; βTTs,i为温度应力作用项; υ为泊松比。
(2) 基岩渗流场方程
| $ \nabla v=\left\lvert\, \frac{\partial e}{\partial t}+\mathrm{Q}\right. $ | (3) |
| $ v=\left\lvert\, \frac{k}{\eta(\nabla p+\rho g \nabla z)}\right. $ | (4) |
式中: t为时间,s; e为岩块体积应变,无量纲; v为基质中的流体速度,m/s; Q为渗流源汇项,1/s; k为基质渗透率,m2; η为流体的动力黏度,Pa·s; ρ为流体密度,kg/m3; g为重力加速度,m/s2; z为垂直坐标,m。
(3) 基岩温度场方程
| $ c_{\mathrm{s}} \rho_{\mathrm{s}} \frac{\partial T_{\mathrm{s}}}{\partial t}=\lambda_{\mathrm{s}} \nabla^2 T_{\mathrm{s}}+W $ | (5) |
式中: cs为基岩比热容,J/(kg·K); ρs为基岩密度,kg/m3; λs为基岩导热系数,W/(m·K); W为热源,W/m3。
1.2 裂缝控制方程(1) 裂缝应力场方程
| $ u_{\mathrm{n}}=\frac{\sigma_{\mathrm{n}}^{\prime}}{k_{\mathrm{n}}}, u_{\mathrm{s}}=\frac{\sigma_{\mathrm{s}}^{\prime}}{k_{\mathrm{s}}} $ | (6) |
| $ \sigma_{\mathrm{n}}^{\prime}=\sigma_{\mathrm{n}}-p, \sigma_{\mathrm{s}}^{\prime}=\sigma_{\mathrm{s}} $ | (7) |
式中: σ′为有效应力,Pa; k为刚度,Pa/m; 下角标n,s分别表示法向和切向。
(2) 裂缝渗流场方程
| $ \nabla_\tau\left(-d_{\mathrm{f}} \frac{k_{\mathrm{f}}}{\eta} \nabla p\right)=-d_{\mathrm{f}} \frac{\partial e_{\mathrm{f}}}{\partial t}-\frac{k_{\mathrm{f}}}{\eta} \frac{\partial p}{\partial n} $ | (8) |
式中: df为裂缝面宽度,m; ∇τ为沿裂缝切向求导; kf为裂缝渗透率,m2; ef为裂缝面的体积应变,无量纲; n为裂缝面的法向。
(3) 裂缝温度场方程
| $ d_{\mathrm{f}} \rho_{\mathrm{f}} c_{\mathrm{f}} \frac{\partial T_{\mathrm{f}}}{\partial t}+d_{\mathrm{f}} \rho_{\mathrm{f}} c_{\mathrm{f}} v_{\mathrm{f}} \nabla_\tau T_{\mathrm{f}}=d_{\mathrm{f}} \nabla_\tau\left(\lambda_{\mathrm{f}} \nabla_\tau T_{\mathrm{f}}\right) $ | (9) |
式中: ρf为流体密度,kg/m3; cf为流体比热容,J/(kg·K); vf为裂缝内流体流速,m/s; λf为流体导热系数,W/(m·K)。
1.3 热-流-固耦合关系(1) 孔渗特性与应力的耦合关系
应力场变化影响裂缝的孔隙度和渗透率,由于裂缝是流体运移的主要通道,渗透率和孔隙度的变化将直接影响系统的热交换效率。基于以往研究[24-26],裂缝孔隙度和渗透率与应力的关系式为
| $ \varphi=1-\frac{\left(1-\varphi_0\right)}{1+\varepsilon_{\mathrm{v}}}\left(1-\frac{1}{K_{\mathrm{s}}} \Delta p+\beta \Delta T\right) $ | (10) |
| $ K=\frac{K_0}{1+\varepsilon_{\mathrm{V}}}\left[1+\frac{\varepsilon_{\mathrm{V}}}{\varphi_0}-\frac{\beta\left(T-T_0\right)\left(1-\varphi_0\right)}{\varphi_0}\right]^3 $ | (11) |
式中: φ0为裂缝初始孔隙率; KS为裂缝体积模量,Pa; εV为体积应变,无量纲; β为干热岩储层热膨胀系数,与温度存在非线性关系,K-1; T为干热岩储层温度,K; K0为裂缝初始渗透率,m2; T0为干热岩储层初始温度,K。
基岩孔隙度和渗透率的变化规律为
| $ \varphi=\left(\varphi_0-\varphi_{\mathrm{r}}\right) \exp \left(-\alpha_{\varphi} \bar{\sigma}_{\mathrm{V}}\right)+\varphi_{\mathrm{r}} $ | (12) |
| $ k=k_0\left(\frac{\varphi}{\varphi_0}\right)^3 $ | (13) |
其中: $\bar{\sigma}_{\mathrm{V}}=\left(\sigma_1+\sigma_2+\sigma_3\right) / 3-\alpha_{\mathrm{B}} p, \alpha_{\varphi}=5 \times 10^{-8} \mathrm{~Pa}^{-1}。$ 式中: αB为Biot固结系数,取值为0.95;φ0为无应力状态孔隙度,无量纲; φr为残余孔隙度,无量纲; k0为无应力状态基质渗透率,m2; p为孔隙应力,Pa; σ为应力,Pa; σV为有效应力,Pa; αφ为孔隙度应力敏感系数,Pa-1。
(2) 流体性质的变化
CO2的密度和黏度随压力与温度的变化而变化,这些参数可通过CMGwinprop相态模拟软件进行计算[27]。此外,CO2的比热容与温度的关系[28]可表示为
| $ C_{\mathrm{CO}_2}=1759.8+7.4 T-0.05 T^2 $ | (14) |
式中: CCO2为CO2的比热容,J/(kg·℃); T为温度,℃。
1.4 求解算法研究采用COMSOL Multiphysics平台建立THM耦合模型,基于分离式瞬态求解器实现多物理场顺序耦合,数值求解过程采用Newton-Raphson非线性迭代方法,全局收敛容差设置为1e-5,具体求解流程如下:
(1) 初始化: 设定模型中所有物理场的初始条件。
(2) 时间步离散: 将瞬态过程离散为时间步序列,采用向后差分法进行时间积分。
(3) 物理场分离求解: 在每个时间步内,采用Newton-Raphson非线性迭代方法来求解方程。依次求解力学场、渗流场和温度场,并通过场间变量传递实现耦合。设场变量为u,控制方程为F(u)= 0,则牛顿迭代步骤为
| $ J\left(u_k\right) \Delta u=-F\left(u_k\right) $ | (15) |
| $ u_{k+1}=u_k+\alpha \Delta u $ | (16) |
式中: $J=\frac{\partial F}{\partial u}$为雅可比矩阵(系统矩阵); Δu为解的增量; α为阻尼因子(可选,用于增强收敛性)。
(4) 收敛判据: 全局容差设为1e-5,当连续2次迭代结果的相对误差满足max(||δu||,||δp||,||δT||)<1e-5时判定收敛,进入下一时间步计算。
(5) 耦合参数传递: 通过PDE弱形式实现场间双向耦合,包括应力场对孔隙度的修正[式(12)—式(13)]、渗流场压力对有效应力的反馈[式(1)]、温度场引起的热应力[式(2)]及CO2物性参数的温度-压力依赖性[式(14)]。
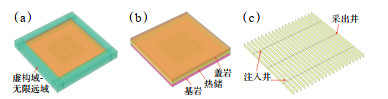
2 数值模型及参数 2.1 基本参数考虑到实际地层结构复杂,难以实现三维精准建模,为简化计算,通过调研相关文献并借鉴已有研究[17],构建了理想的增强型地热系统概化模型,便于研究THM耦合下三场演变及取热变化规律。如图 1所示,几何模型自上而下依次为盖岩、干热岩热储和基岩(单层尺寸为2 000 m×2 000 m×60 m),四周为围岩,热储埋深为4 000 m。采用“两注一采”井网布局,生产井居中,两侧对称布置注入井(井间距为300 m,井长为1 000 m),垂直注入井/生产井均匀布置21条压裂裂缝(缝间距为50 m,缝宽为2 mm)。
|
下载原图 图 1 数值模型(a),盖岩-热储-基岩(b)和井网及缝网布置(c) Fig. 1 Numerical model (a), caprock-thermal reservoir-bedrock (b) and layout of well pattern and fracture network (c) |
在渗流场中,注入井与生产井分别设置为46 MPa和40 MPa的定压边界条件,初始孔隙压力为40 MPa,上下表面为不可渗透边界,注入的超临界CO2温度为80 ℃,储层初始温度为200 ℃,上下表面绝热,四周为定温条件。应力场采用固定约束边界条件,采用瞬态模拟进行求解,计算总时长为30 a,步长设置为0.1 a。
基于现场经验与既有模拟参数,模型设定为: ①盖岩/基岩,弹性模量为35 GPa,密度为2 700 kg/m3,泊松比为0.28,比热容为950 J/(kg·K),渗透率为1×10-4 mD,热膨胀系数为3.4×10-6 K-1,孔隙度为0.01,导热系数为1.0 W/(m·K),Biot系数为0.95; ②热储,弹性模量为40 GPa,密度为2 500 kg/m3,泊松比为0.25,渗透率为1×10-2 mD,热膨胀系数为3.6×10-6 K-1,孔隙度为0.02,导热系数为3.1 W/(m·K),比热容和Biot系数同盖岩; ③裂缝,宽度为2 mm,法向/切向刚度为100/30 GPa·m-1,渗透率为30 D,孔隙度为0.30,比热容为850 J/(kg·K)。
2.2 热补偿模拟热补偿作用主要由深部高温基岩提供,同时盖岩和围岩也起到保温作用,本次提出了一种多源热补偿数值模拟方法,通过整合基岩、盖岩及围岩的热响应机制,系统描述了干热岩热储开发中的热量动态平衡过程。在模型构建中,基岩热源采用大地热流边界,模拟通过热传导向上为热储补充热量; 盖岩采用定温边界,表征对热储顶部热量的封闭作用; 围岩则建立为无限单元,反映周围岩体通过缓慢热传导维持系统温度稳定的特性。模拟流程分为2个阶段,首先进行稳态分析,建立初始热平衡状态; 随后注入低温CO2进行瞬态热开采模拟,从而实现盖岩和基岩热补偿作用的CO2-EGS干热岩热储开发数值模拟。
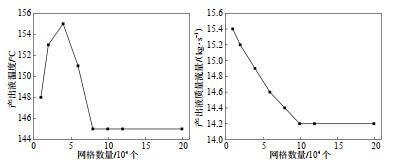
2.3 网格无关性验证图 2展示了第30年产出液质量流量及温度随网格数量的变化规律,当网格数低于99 360个时,质量流量计算结果表现出明显的网格依赖性; 当网格数大于该临界值后,模拟结果趋于稳定。根据网格独立性验证原则,研究采用99 360个单元构建计算模型,在保证结果精度的同时实现计算效率的优化。
|
下载原图 图 2 产出液温度和质量流量随网格数量变化曲线 Fig. 2 Variation of temperature and mass flow rate of the produced liquid with the number of grids |
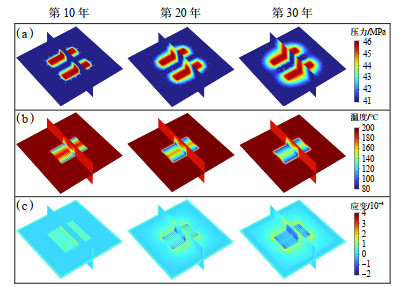
图 3展示了超临界CO2注入EGS储层10年后、20年后及30年后渗流场、温度场及应变场的演化特征。
|
下载原图 图 3 热储内渗流场(a)、温度场(b)和应变场(c)随时间演化规律分布 Fig. 3 Evolution law of seepage field (a), temperature field (b) and strain field (c) inside the thermal storage over time |
图 3a展示了渗流场的特征,主要通过孔隙压力分布和流线分布来表征。水平井通过分布式注入点注入大量超临界CO2,并沿高渗透性多簇裂缝快速流向生产井,少量渗入热储基质。由于裂缝导压能力强,其压力迅速上升,随后基质压力也逐渐升高,流速分布表明,裂缝内的流速明显高于基质(箭头长度代表流速大小)。
图 3b展示了不同时刻储层内的温度分布。注入初期低温CO2优先沿裂缝与热储基质进行热交换,形成低温区,而生产井区域温度保持稳定,确保持续热量输出。随着注入时间延长,低温区向生产井扩展,与直井相比,水平井注入量更大,波及范围更广,热储温度下降更快。同时,注采井间的贯穿裂缝形成高效热交换通道,明显提高了热交换效率。
在应力场研究中,重点关注裂缝宽度变化对EGS储层渗透率和产热效率的影响。图 3c展示了不同时刻裂缝面上的正应变分布,热交换导致基质收缩(应变值为负),裂缝宽度增大(应变值为正),渗透率随之增大,增强了渗流场中流体的流动。随着时间的推移,正应变区域逐渐扩展,CO2在裂缝中的运移速度加快,进一步促进了温度场中的热传递。
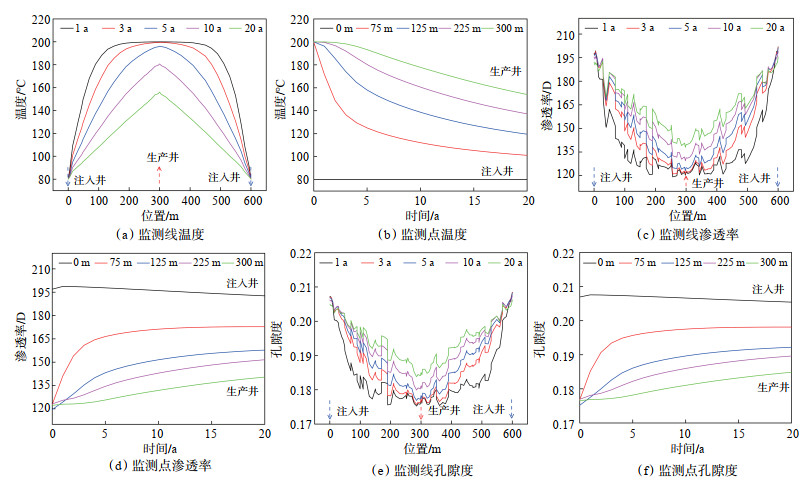
为进一步研究热储内部温度演化规律,在3口水平井中点连线处设置监测线,沿监测线提取不同开采年份1 a,3 a,5 a,10 a,20 a的温度分布(图 4a),并在监测线上选取0,75 m,125 m,225 m,300 m 5个监测点绘制温度随时间的变化曲线(图 4b),注入井附近温度最低(恒温80 ℃),并向生产井方向逐渐升高,除注入井处,各监测点温度随开采时间持续下降,低温区域范围逐年扩大,开采至第3年时已扩展至生产井区域。
|
下载原图 图 4 监测线和监测点的温度、渗透率与孔隙度随时间变化曲线 Fig. 4 Temperature, permeability and porosity change over time of monitoring lines and monitoring points |
应力场作用下裂缝渗透率和孔隙度的演化规律(图 4c—4f)所示,渗透率和孔隙度均具有从注入井向生产井递减的分布特征。在应力-温度耦合作用下,裂缝附近基质受冷收缩导致渗透率和孔隙度逐年递增(注入井温度恒定,渗透率与孔隙度保持稳定),且距注入井越近,冷缩效应越明显,渗透率和孔隙度越大。值得注意的是,监测线渗透率和孔隙度曲线局部出现剧烈波动,主要源于局部应力扰动,包括裂缝尖端应力集中、相邻裂缝应力干扰及低温CO2注入引发的剪切滑移等因素。
3.2 控制因素主要从THM耦合、井网参数和缝网参数3个方面分析对产热的影响,其中,井网参数包括水平井段长度、井间距和注采模式; 缝网参数包括缝间距、缝宽和缝高。
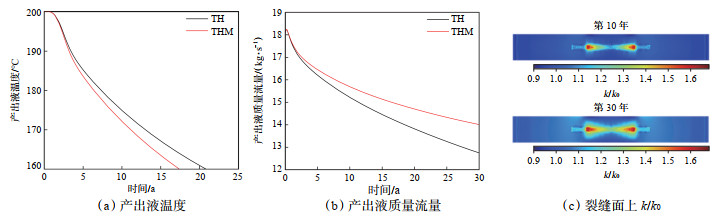
3.2.1 THM耦合对产热的影响通过对比TH耦合和THM耦合模型,分析产出液温度与质量流量的变化特征(图 5a,5b),结果表明,相较于TH耦合模型,THM模型中温度下降速率更快,同时产出液质量流量增加了5.76%。应力场作用下,裂缝渗透率增大(渗透率与初始值之比> 1,图 5c),不仅提高了质量流量,还加速了热储裂缝周围温度场的下降,明显影响了CO2-EGS的取热性能。因此,数值模拟中不应忽视应力场的影响,以产出液温度160 ℃为开发终止条件时,TH耦合模型和THM耦合模型预测的生产周期分别为20.4 a和17.1 a,表明TH耦合模型对生产周期的预测偏长。
|
下载原图 图 5 产出液温度和质量流量随时间变化曲线 Fig. 5 Variation of temperature and mass flow rate of the produced liquid with time |
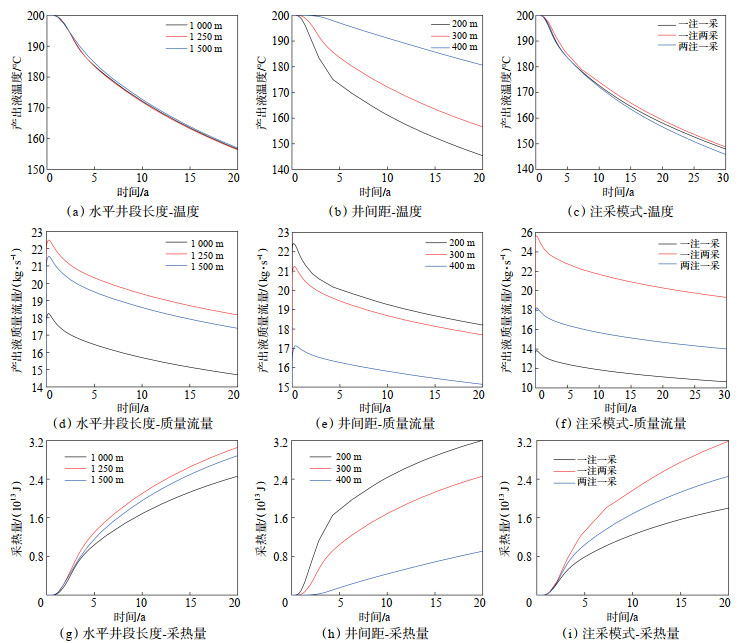
保持其他参数设置不变,模拟改变水平井段长度、井间距和注采模式对产出液温度、质量流量和采热量的影响(图 6)。
|
下载原图 图 6 不同井网参数下产出液温度、质量流量和采热量随时间变化曲线 Fig. 6 Variation of temperature, mass flow rate and heat recovery of produced liquid over time under different well pattern parameters |
图 6a、图 6d和图 6g展示了水平井段长度对CO2-EGS系统产出液温度与质量流量的影响,图 6a水平井段长度对产出液温度的影响较小。在第20年时,1 000 m,1 250 m和1 500 m井长的温度分别为155.0 ℃,155.5 ℃和157.7 ℃,差异不到3%。图 6b和图 6g表明,水平井段长度对质量流量和采热量的影响呈非线性特征,当井长从1 000 m增至1 250 m时,流量和采热量增加,然而当井长增至1 500 m时,流量和采热量却小幅下降。综合分析表明,水平井长度并非越长越好,建议1 250 m为宜。
图 6b、图 6e和图 6h展示了井间距对CO2-EGS系统产出液温度、质量流量和采热量的影响,随着井间距从200 m增至400 m时,第20年产出液温度从143.2 ℃明显上升至180.3 ℃(增幅26.0%),而质量流量则从15.1 kg/s下降至12.1 kg/s(降幅19.9%),采热量也从3.2×1013 J下降至0.92×1013 J。井间距增大(裂缝长度延伸)延长了CO2的取热路径,提高了热交换效率,减缓了温度下降,但降低了注入井与生产井之间的压力梯度(根据达西定律),导致质量流量下降。综合考虑,建议将水平井间距设置为300 m。
图 6c、图 6f和图 6i展示了注采模式对CO2-EGS系统产出液温度与质量流量的影响,图 6c注采模式对产出液温度的影响较小。3种模式(一注一采、一注两采、两注一采)在第20年的温度分别为157.7 ℃,158.9 ℃和156.1 ℃,差异不足2.8%。图 6f一注两采的流量为20.2 kg/s,较一注一采(流量为11.1 kg/s)和两注一采(流量为14.85 kg/s)分别提升了81.8% 和36.1%。图 6i一注两采的采热量为3.2×1013 J,较一注一采(采热量为1.8×1013 J)和两注一采(采热量为2.5×1013 J)分别提升了77.8% 和28.0%。综合考虑,建议采用一注两采模式。
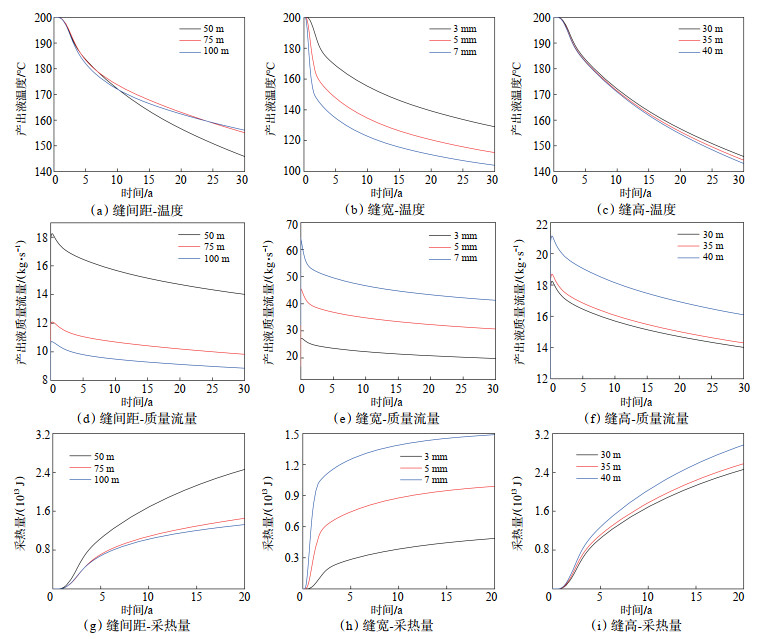
3.2.3 缝网参数对产热的影响保持其他参数设置不变,模拟改变缝间距、缝宽和缝高对产出液温度、质量流量和采热量的影响(图 7)。
|
下载原图 图 7 不同缝网参数下产出液温度、质量流量和采热量随时间变化曲线 Fig. 7 Variation of temperature, mass flow rate and heat recovery of produced liquid under different fracture network parameters |
图 7a、图 7d和图 7g展示了缝间距对CO2-EGS系统产出液温度、质量流量和采热量的影响,随着缝间距从50 m增至100 m时,第20年产出液温度从157.7 ℃上升至162.8 ℃,但在75 m间距时达到峰值为163.5 ℃,表明温度提升存在阈值。质量流量从14.85 kg/s急剧下降至9.1 kg/s时,降幅达63.2%,采热量也从2.5×1013 J急剧下降至1.3× 1013 J,降幅达92.3%。由于模型几何尺寸(除缝间距)固定,增大缝间距导致裂缝数量减少(流动路径减少),导致质量流量明显下降,而流入热储的低温CO2减少,减缓了热储降温,温度上升。综合考虑,建议将缝间距设置为75 m。
图 7b、图 7e和图 7h展示了缝宽对CO2-EGS系统产出液温度、质量流量和采热量的影响,随着缝宽从3 mm增加至7 mm,第20年产出液温度从139.2 ℃明显下降至110.2 ℃,降幅达到20.2%,而质量流量从20.8 kg/s增加至43.1 kg/s,增幅达107.2%,采热量也从4.9×1013 J增加至1.5×1014 J,增幅达206.1%。缝宽增大提升了裂缝的导流能力,但较宽的裂缝加速了低温CO2的流动,缩短了流体与热储基质的热交换时间,同时大量低温CO2的流入导致热储快速降温。尽管7 mm和5 mm的缝宽实现了流量峰值,但其温度无法满足开发需求。综合考虑,建议将缝宽设置为3 mm。
图 7c、图 7f和图 7i展示了缝高对CO2-EGS系统产出液温度、质量流量和采热量的影响,随着缝高从30 m增至40 m时,第20年产出液温度由157.7 ℃缓慢降至153.5 ℃,降幅仅为2.7%,而质量流量则从14.85 kg/s提升至16.9 kg/s,增幅达13.8%,采热量也从2.5×1013 J提升至2.9×1013 J,增幅达16.0%。其机制与缝宽类似,但垂向裂缝延伸使CO2流动路径深入热储内部,与基岩和盖层形成立体热交换网络,厚层基岩的热容持续补充热量,减缓了温度下降。相比之下,缝宽增加仅水平扩展裂缝,流体快速通过薄层裂缝,无法与侧向围岩充分接触,导致产出液温度降幅比缝高大7倍以上。综合考虑,建议将缝高设置为40 m。
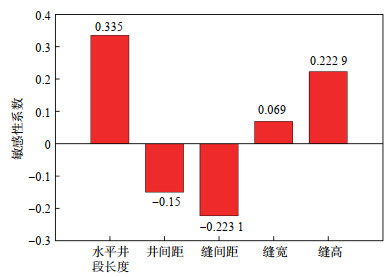
3.2.4 多因素敏感性排序采用以下步骤对影响因素进行敏感性分析,以确定水平井段长度、井间距、缝间距、缝宽和缝高与采热量之间的定量关系(图 8): ①计算各影响因素参数取值的变化率; ②计算各因素变化对采热量的影响率; ③用采热量的变化率除以参数取值的变化率,得到基准值; ④将所有参数的基准值进行归一化处理,得到敏感性系数。
|
下载原图 图 8 各参数的敏感性系数 Fig. 8 Sensitivity coefficient of each parameter |
如图 8所示,各影响因素的敏感性系数从大到小排序依次为水平井长度、缝间距、缝高、井间距和缝宽。其中,水平井长度、缝宽和缝高与采热量呈正相关关系,而井间距和缝间距则与采热量呈负相关关系。
4 结论(1) 通过重构热-流-固耦合关系,修正了裂缝孔隙度和渗透率与应力的函数关系,改进CO2密度、黏度和比热容随压力与温度的变化关系,建立了CO2-EGS干热岩热储水平井开发数学模型,为CO2- EGS干热岩水平井开发提供了完善的多场耦合理论体系和有效的数值模拟方法。
(2) 通过引入基岩控制方程、裂缝控制方程和热-流-固耦合关系,并借助COMSOL软件考虑基岩、盖岩和围岩的热补偿作用,提出了考虑多源热补偿方法的多簇压裂条件下CO2-EGS干热岩热储水平井开发数值模型。
(3) 利用数值模型开展CO2-EGS干热岩热储水平井开发模拟,揭示了干热岩温度场、渗流场及应力场的演化规律,明确了水平井井网、多簇压裂缝网以及超临界CO2的性质直接影响CO2-EGS的演化过程。
(4) 通过数值模拟并以最大采热量为目标,获取了CO2-EGS的控制因素为THM耦合机制、水平井井网参数和多簇压裂缝网参数。THM耦合相对于TH耦合其产出液质量流量提高5.76%,但取热周期缩短3.3 a; 合理的水平井井网参数为一注两采、水平井长度为1 250 m、水平井井距为300 m; 最优的缝网参数为缝间距75 m、缝宽3 mm、缝高40 m。
| [1] |
屈卫华, 田野, 董常春, 等. 松辽盆地德惠断陷白垩系烃源岩特征及其控藏作用. 岩性油气藏, 2024, 36(6): 122-134. QU Weihua, TIAN Ye, DONG Changchun, et al. Characteristics of Cretaceous source rocks and their controlling effect on hydrocarbon accumulation in Dehui Fault Depression, Songliao Basin. Lithologic Reservoirs, 2024, 36(6): 122-134. DOI:10.12108/yxyqc.20240612 |
| [2] |
刘世奇, 皇凡生, 杜瑞斌, 等. CO2地质封存与利用示范工程进展及典型案例分析. 煤田地质与勘探, 2023, 51(2): 158-174. LIU Shiqi, HUANG Fansheng, DU Ruibin, et al. Progress and typical case analysis of demonstration projects of the geological sequestration and utilization of CO2. Coal Geology & Exploration, 2023, 51(2): 158-174. |
| [3] |
桑树勋, 袁亮, 刘世奇, 等. 碳中和地质技术及其煤炭低碳化应用前瞻. 煤炭学报, 2022, 47(4): 1430-1451. SANG Shuxun, YUAN Liang, LIU Shiqi, et al. Geological technology for carbon neutrality and its application prospect for low carbon coal exploitation and utilization. Journal of China Coal Society, 2022, 47(4): 1430-1451. |
| [4] |
GENTZIS T. Subsurface sequestration of carbon dioxide: An overview from an Alberta(Canada)perspective. International Journal of Coal Geology, 2000, 43(1/4): 287-305. |
| [5] |
王社教, 施亦做, 方朝合, 等. 中国油田地热开发利用现状与发展方向. 岩性油气藏, 2024, 36(2): 23-32. WANG Shejiao, SHI Yizuo, FANG Chaohe, et al. Status and development trends of geothermal development and utilization in oilfields of China. Lithologic Reservoirs, 2024, 36(2): 23-32. DOI:10.12108/yxyqc.20240203 |
| [6] |
崔传智, 李静, 吴忠维. 扩散吸附作用下CO2非混相驱微观渗流特征模拟. 岩性油气藏, 2024, 36(6): 181-188. CUI Chuanzhi, LI Jing, WU Zhongwei. Simulation of microscopic seepage characteristics of CO2 immiscible flooding under the effect of diffusion and adsorption. Lithologic Reservoirs, 2024, 36(6): 181-188. DOI:10.12108/yxyqc.20240617 |
| [7] |
杨兆臣, 卢迎波, 杨果, 等. 中深层稠油水平井前置CO2蓄能压裂技术. 岩性油气藏, 2024, 36(1): 178-184. YANG Zhaochen, LU Yingbo, YANG Guo, et al. Pre-CO2 energy storage fracturing technology in horizontal wells for medium-deep heavy oil. Lithologic Reservoirs, 2024, 36(1): 178-184. DOI:10.12108/yxyqc.20240117 |
| [8] |
卜宪标, 郭志鹏, 李华山, 等. CO2单井增强地热系统取热性能研究. 新能源进展, 2022, 10(6): 509-518. BU Xianbiao, GUO Zhipeng, LI Huashan, et al. Heat extraction performance of CO2 single-well enhanced geothermal system. Advances in New and Renewable Energy, 2022, 10(6): 509-518. DOI:10.3969/j.issn.2095-560X.2022.06.003 |
| [9] |
郭平, 许清华, 孙振, 等. 天然气藏CO2驱及地质埋存技术研究进展. 岩性油气藏, 2016, 28(3): 6-11. GUO Ping, XU Qinghua, SUN Zhen, et al. Research progress of CO 2 flooding and geological storage in gas reservoirs. Lithologic Reservoirs, 2016, 28(3): 6-11. DOI:10.3969/j.issn.1673-8926.2016.03.002 |
| [10] |
LIU Shuyang, SUN Baojiang, XU Jianchun, et al. Study on competitive adsorption and displacing properties of CO2 enhanced shale gas recovery: Advances and challenges. Geofluids, 2020, 15: 6657995. |
| [11] |
张烈辉, 曹成, 文绍牧, 等. 碳达峰碳中和背景下发展CO2- EGR的思考. 天然气工业, 2023, 43(1): 13-22. ZHANG Liehui, CAO Cheng, WEN Shaomu, et al. Thoughts on the development of CO2-EGR under the background of carbon peak and carbon neutrality. Natural Gas Industry, 2023, 43(1): 13-22. |
| [12] |
PRUESS K. Enhanced geothermal systems(EGS): Comparing water with CO 2 as heat transmission fluids[R]. Dallas, Geothermal Energy Utilization Conference, 2008.
|
| [13] |
RANDOLPH J B, SAAR M O. Coupling carbon dioxide sequestration with geothermal energy capture in naturally permeable, porous geologic formations: Implications for CO2 sequestration. Energy Procedia, 2011, 4: 2206-2213. DOI:10.1016/j.egypro.2011.02.108 |
| [14] |
GHASSEMI A, ZHOU X. A three-dimensional thermo-poroelastic model for fracture response to injection/extraction in enhanced geothermal systems. Geothermics, 2011, 40(1): 39-49. DOI:10.1016/j.geothermics.2010.12.001 |
| [15] |
KOH J, ROSHAN H, RAHMAN S S. A numerical study on the long term thermo-poroelastic effects of cold water injection into naturally fractured geothermal reservoirs. Computers and Geotechnics, 2011, 38: 669-682. DOI:10.1016/j.compgeo.2011.03.007 |
| [16] |
JING Yani, JING Zhenzi, RICHARDS W J, et al. A simple 3-D thermoelastic model for assessment of the long-term performance of the Hijiori deep geothermal reservoir. Journal of Volcanology and Geothermal Research, 2014, 269: 14-22. |
| [17] |
曹文炅, 黄文博, 蒋方明. 地下热流固耦合对EGS热开采的影响. 新能源进展, 2015, 3(6): 444-451. CAO Wenjiong, HUANG Wenbo, JIANG Fangming. The thermalhydraulic-mechanical coupling effects on heat extraction of enhanced geothermal systems. Advances in New and Renewable Energy, 2015, 3(6): 444-451. |
| [18] |
HICKS T W, PINE R J, RICHARDS W J, et al. A hydrothermos-mechanical numerical model for HDR geothermal reservoir evaluation. International Journal of Rock Mechanics & Mining Sciences, 1996, 33(5): 499-511. |
| [19] |
TARON J, ELSWORTH D. Thermal-hydrologic-mechanicalchemical processes in the evolution of engineered geothermal reservoirs. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(5): 855-864. |
| [20] |
TARON J, ELSWORTH D, MIN K B. Numerical simulation of thermal-hydrologic-mechanical-chemical processes in deformable, fractured porous media. International Journal of Rock Mechanics & Mining Sciences, 2009, 46(5): 842-854. |
| [21] |
MCDERMOTT C I, RANDRIAMANJATOSOAA R L, TENZER H, et al. Simulation of heat extraction from crystalline rocks: The influence of coupled processes on differential reservoir cooling. Geothermics, 2006, 35(3): 321-344. |
| [22] |
SUN Yuexue, ZHANG Xiao, LI Xianghui, et al. Study on the intrinsic mechanisms underlying enhanced geothermal system (EGS)heat transfer performance differences in multi-wells. Energy Conversion and Management, 2023, 292: 117361. |
| [23] |
李静岩, 刘中良, 周宇, 等. CO2羽流地热系统热开采过程热流固耦合模型及数值模拟研究. 化工学报, 2019, 70(1): 72-82. LI Jingyan, LIU Zhongliang, ZHOU Yu, et al. Study of thermal-hydrologic-mechanical numerical simulation model on CO2 plume geothermal system. CIESC Journal, 2019, 70(1): 72-82. |
| [24] |
李培超, 孔祥言, 卢德唐. 饱和多孔介质流固耦合渗流的数学模型. 水动力学研究与进展, 2003, 18(4): 419-426. LI Peichao, KONG Xiangyan, LU Detang. Mathematical modeling of flow in saturated porous media on account of fluidstructure coupling effect. Journal of Hydrodynamics, 2003, 18(4): 419-426. |
| [25] |
戴永浩, 陈卫忠, 伍国军, 等. 非饱和岩体弹塑性损伤模型研究与应用. 岩石力学与工程学报, 2008, 27(4): 728-735. DAI Yonghao, CHEN Weizhong, WU Guojun, et al. Study on elastoplastic damage model of unsaturated rock mass and its application. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 728-735. |
| [26] |
王辉. 孔隙型热储开采适宜区识别及采灌模式优化研究[D]. 青岛: 山东大学, 2023. WANG Hui. Research on identification of suitable exploitation area and optimization of exploitation and reinjection mode for porous medium reservoir[D]. Qingdao: Shandong University, 2023. |
| [27] |
LI Jiawei, LI Zi, YUAN Wanju, et al. Numerical investigation of liquid and supercritical CO2 flow behaviors through 3D self-affine rough fractures. Fuel, 2019, 251: 669-682. |
| [28] |
CUI Guodong, ZHANG Liang, REN Bo, et al. Geothermal exploitation from depleted high temperature gas reservoirs via recycling supercritical CO2: Heat mining rate and salt precipitation effects. Applied Energy, 2016, 183: 837-852. |
 2025, Vol. 37
2025, Vol. 37




