根据天然气藏分类评价标准[1],将压力系数高于1.3的气藏定义为异常高压气藏(Overpressured gas reservoirs)。在中国,异常高压有水气藏主要分布在塔里木盆地和四川盆地[2],如安岳气田龙王庙组、克拉2气田等,压力系数为1.34~2.20。异常高压有水气藏与异常高压无水气藏的物质平衡压降曲线形态有所不同,呈现出上移的“直线形”形态。异常高压无水气藏压降曲线仅受岩石和流体压缩作用,而异常高压有水气藏除受上述2种能量的作用之外,还会受到“均匀能量补充水侵”的作用[3-4]。安岳气田龙王庙组和克拉2气田在矿场实践中均已测试到这类压降曲线。
目前,针对异常高压气藏物质平衡方程的研究主要是考虑无水形式。可分为2类:第1类已知岩石和流体压缩系数。Ramagost等[5]在修正因子中考虑了岩石和水的压缩性,建立了线性回归法;Bourgoyne等[6]建立了考虑岩石高压缩性和水侵的二元回归法;Hammerlindl[7]建立了修正压缩系数的物质平衡法,可更好的用于预测气藏废弃压力;Fetkovich等[8]定义了累积有效压缩系数,并由生产历史数据拟合求解气藏压降曲线;陈元千[9-10]推导了二段拐点式和压力2次方形式的异常高压气藏物质平衡方程;李传亮[11]建立了直线形生产指示曲线,将岩石和流体压缩系数整合到拟压力中。第2类不需要岩石和流体压缩系数,采用由生产压力数据确定的累积有效压缩系数,主要有Roach[12]直线回归法,该方法对气藏原始压力较敏感;Ambastha[13]采用典型曲线拟合程序,分析了异常高压气藏的生产动态;Gan等[14]提出了二段式多图版曲线拟合法;Gonzalez等[15]采用了抛物线式多图版曲线拟合法。此外,孙贺东等[16]、秦正山等[17]、岳世俊等[18]、邓成刚等[19]、李冬梅等[20]提出了与上述方法相近似的方法。目前尚未见到关于异常高压有水气藏“直线形”物质平衡方程的相关报导。
基于此,利用Fetkovich定义的累积有效压缩系数概念,引入动态储量采出程度$G_{\mathrm{p}} / G$与$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$的幂指函数经验关系式,推导了异常高压有水气藏“直线形”物质平衡方程,并导出了动态储量和水侵量的计算式。利用6个已开发异常高压有水气藏实例数据,确定出不同气藏的$G_{\mathrm{p}} / G$与$\bar{C}_{e}(p) \Delta p+\omega$的幂指函数经验关系式。与文献计算结果对比,本次建立的异常高压有水气藏物质平衡方程是可靠的。
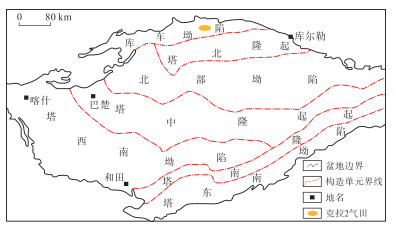
1 地质概况克拉2气田位于新疆维吾尔自治区阿克苏地区拜城县境内,气田紧靠天山南麓。构造上属于塔里木盆地北部的库车坳陷克拉苏构造带东段的一个局部构造,位于克拉苏—依奇克里克构造带西部的克拉苏构造带(图 1)。构造高点海拔-2 000 m,气水界面-2 468 m,储层厚度大于500 m。储层主要为下白垩统巴什基奇克组,在气田范围内分布稳定、砂体连续性较好,泥岩分布零星、断续,为一套纵向和横向上连通性好、沉积厚度大,平面上展布面积广、连片分布的板状砂体。储层平均孔隙度为12.6%,平均渗透率为49.42 mD。气藏中部埋藏深度为3 643~3 871 m,原始地层压力为74.41 MPa,压力系数为1.95~2.20,原始地层温度为100 ℃,地温梯度为2.2 ℃/100 m。气藏具有边、底水块状特征,为大型边底水整装异常高压干气气藏。该气藏2004年底投产,气藏开采较为均衡,2008年确认见水,累产气超过1 400×108 m3。
|
下载原图 图 1 塔里木盆地克拉2气田区域构造位置 Fig. 1 Regional structural location of Kela 2 gas field in Tarim Basin |
岩石有效压缩系数是异常高压气藏物质平衡方程中的关键参数,一般由实验测定或经验公式计算[21-24],但实验值和经验公式往往不具有气藏代表性。针对气藏流体、多孔介质的压缩性以及水体侵入引起的烃类孔隙体积的累计变化量,Fetkovich[8] 提出累积有效压缩系数的概念,若只考虑流体压缩性的贡献,将Fetkovich定义的$\bar{C}_{\mathrm{e}}(p)$改写为
| $ \bar{C}_{\mathrm{e}}(p)=\frac{\bar{C}_{\mathrm{w}} S_{\mathrm{wi}}+\bar{C}_{\mathrm{f}}}{1-S_{\mathrm{wi}}} $ | (1) |
式中:$\bar{C}_{\mathrm{e}}(p)$ 为累积有效压缩系数,$1 / \mathrm{MPa}; ~ S_{\mathrm{wi}}$ 为地层束缚水饱和度,%;$\bar{C}_{\mathrm{w}}$ 为累积束缚水有效压缩系数,$1 / \mathrm{MPa}; \bar{C}_{\mathrm{f}}$ 为累积储层有效压缩系数,$1 / \mathrm{MPa}$。
将文献[25]中式(5)的$C_{\mathrm{e}}$ 项,由式(1)替换,则异常高压有水气藏物质平衡方程可表示为
| $ G_{\mathrm{p}} B_{\mathrm{g}}=G\left(B_{\mathrm{g}}-B_{\mathrm{gi}}\right)+G B_{\mathrm{gi}} \bar{C}_{\mathrm{e}}\left(p_{\mathrm{i}}-p\right)+\left(W_{\mathrm{e}}-W_{\mathrm{p}} B_{\mathrm{w}}\right) $ | (2) |
式中:$G_{\mathrm{p}}$ 为累积产气量,$10^{8} \mathrm{~m}^{3}; B_{\mathrm{g}}$ 为$p$ 压力下的气体体积系数;$G$ 为动态储量,$10^{8} \mathrm{~m}^{3}; B_{\mathrm{gi}}$ 为原始气体体积系数;$p$ 为某开发时间的地层压力,$\mathrm{MPa}; p_{\mathrm{i}}$ 为原始地层压力,$\mathrm{MPa}; W_{\mathrm{e}}$ 为水侵量,$10^{4} \mathrm{~m}^{3}; W_{\mathrm{p}}$ 为累积产水量,$10^{4} \mathrm{~m}^{3}; ~ B_{\mathrm{w}}$ 为地层水体积系数,一般取1.0。
| $ B_{\mathrm{gi}}=\frac{p_{\mathrm{SC}} Z_{\mathrm{i}} T}{p_{\mathrm{i}} T_{\mathrm{SC}}} $ | (3) |
| $ B_{\mathrm{g}} =\frac{p_{\mathrm{SC}} Z T}{p T_{\mathrm{SC}}} $ | (4) |
式中:$p_{\mathrm{SC}}$ 为地面标准压力,$\mathrm{MPa}; Z_{\mathrm{i}}$ 为原始地层压力下的天然气偏差因子;$T$ 为气藏温度,${ }^{\circ} \mathrm{C}; T_{\mathrm{SC}}$ 为地面标准温度,${ }^{\circ} \mathrm{C}; Z$ 为$p$ 压力下的天然气偏差因子。
令
| $ W=W_{\mathrm{e}}-W_{\mathrm{p}} B_{\mathrm{w}} $ | (5) |
式中:$W$ 为存水量,$10^{4} \mathrm{~m}^{3}$;
将式(3)—式(5)代入式(2),公式两边同时除以$G B_{\mathrm{gi}}$,经整理简化得
| $ \frac{p}{Z}\left(1-\bar{C}_{\mathrm{e}}(p) \Delta p-\omega\right)=\frac{p_{\mathrm{i}}}{Z_{\mathrm{i}}}\left(1-\frac{G_{\mathrm{p}}}{G}\right) $ | (6) |
其中:
| $ \Delta p =p_{\mathrm{i}}-p $ | (7) |
| $ \omega =\frac{W}{G B_{\mathrm{gi}}} $ | (8) |
式中:ω为存水体积系数。
$\bar{C}_{\mathrm{e}}(p) \Delta p$ 和$\omega$ 分别为气藏岩石骨架、流体压缩与水体侵入的综合能量。令$R_{\mathrm{D}}=G_{\mathrm{p}} / G$,定义为动态储量采出程度。假设$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与$G_{\mathrm{p}} / G$ 符合幂指函数关系,则有
| $ \bar{C}_{\mathrm{e}}(p) \Delta p+\omega=A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B} $ | (9) |
式中:A,B为幂指函数拟合系数。
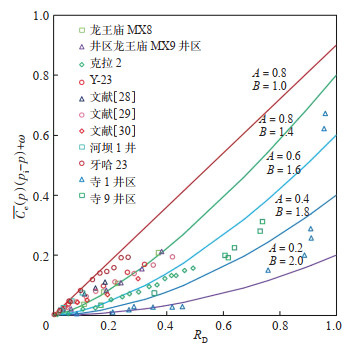
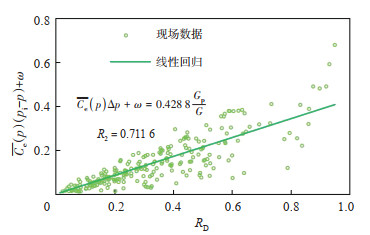
式(9)由矿场数据统计发现,中国11个异常高压有水气藏的数据点和理论线的关系如图 2所示。$A, B$ 值可以揭示不同的水侵方式:若气藏为早期水侵,则$A$ 值越大;若气藏为中后期水侵,则$B$ 值越大。不同气藏的水侵方式不同,故不同气藏的$A, B$值也不相同(图 2)。根据文献[3, 26-32]的矿场数据,中国11个异常高压有水气藏的$A$ 值为$0.3 \sim 0.9, B$ 值为$1 \sim 2$。值得注意的是,水侵主要发生在开发早期的气藏$A$ 值高于异常高压无水气藏$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与$G_{\mathrm{p}} / G$ 线性拟合关系中斜率$\lambda$ 的值为0.4288(图 3),$B$ 值近似于1,如牙哈23气藏的$A, B$ 值分别为0.825和1。
|
下载原图 图 2 异常高压有水气藏的$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与RD关系 Fig. 2 Relationship between $\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ and RD of abnormal high pressure gas reservoirs with aquifer |
|
下载原图 图 3 异常高压无水气藏的$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega-R_{\mathrm{D}}$回归拟合曲线 Fig. 3 Regression fitting curve of $\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ and RD of abnormal high pressure anhydrous gas reservoirs |
将式(6)变形得
| $ \frac{\frac{p}{Z}}{\frac{p_{\mathrm{i}}}{Z_{\mathrm{i}}}}=\frac{1-\frac{G_{\mathrm{p}}}{G}}{1-\overline{C_{\mathrm{e}}}(p) \Delta p-\omega} $ | (10) |
分析公式(10),因$\frac{p / Z}{p_{\mathrm{i}} / Z_{\mathrm{i}}} < 1$,故$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega < G_{\mathrm{p}} / G_{\circ}$
将式(9)代入式(10)得
| $ \frac{\frac{p}{Z}}{\frac{p_{\mathrm{i}}}{Z_{\mathrm{i}}}}=\frac{1-\frac{G_{\mathrm{p}}}{G}}{1-A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}} $ | (11) |
将式(11)中右边的$\frac{1}{1-A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}}$ 项按泰勒级数(Taylor series)展开,得
| $ \frac{1}{1-A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}}=1+A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}+\left[A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}\right]^{2}+\cdots $ | (12) |
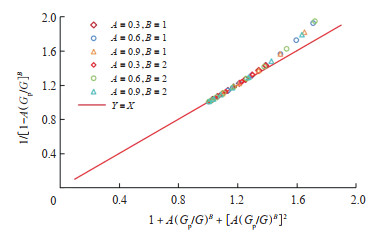
因$G_{\mathrm{p}} / G < 1$,在$A$ 值为$0.3 \sim 0.9, B$ 值为$1 \sim 2$的条件下,由图 4可看出,式(12)的值主要由前2项贡献。
|
下载原图 图 4 泰勒展开式计算对比 Fig. 4 Comparison of Taylor series calculations |
取式(12)中的前2项,代入式(11),得
| $ \frac{\frac{p}{Z}}{\frac{p_{\mathrm{i}}}{Z_{\mathrm{i}}}}=1-\frac{G_{\mathrm{p}}}{G}+A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B}-A\left(\frac{G_{\mathrm{p}}}{G}\right)^{B+1} $ | (13) |
令$p_{\mathrm{D}}=\frac{p / Z}{p_{\mathrm{i}} / Z_{\mathrm{i}}}$,定义为无因次拟压力,$R_{\mathrm{D}}=G_{\mathrm{p}} / G$,定义为动态储量采出程度。式(13)可改写为
| $ 1-p_{\mathrm{D}}=R_{\mathrm{D}}-A R_{\mathrm{D}}^{\;B}+A R_{\mathrm{D}}^{\;B+1} $ | (14) |
式(14)即为幂指函数形式的异常高压有水气藏物质平衡方程。若$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 不贡献能量,则$A, B$ 值均为0,式(14)即为定容气藏物质平衡方程。若$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与$G_{\mathrm{p}} / G$ 符合线性关系,则$B=0$,$A=\lambda$,式(14)即为异常高压无水气藏物质平衡方程。
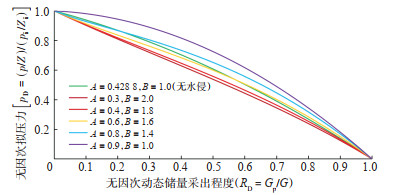
根据不同的$A(0.3 \sim 0.9), B(1 \sim 2)$ 和$R_{\mathrm{D}}(0 \sim 1)$值绘制无因次$R_{\mathrm{D}}-p_{\mathrm{D}}$ 图版(图 5)。
|
下载原图 图 5 无因次RD-pD图版 Fig. 5 Dimensionless of RD and pD |
假设异常高压有水气藏生产早期水侵量较小,而忽略不计时,式(14)可写为
| $ 1-p_{\mathrm{D}}=(1-\lambda) R_{\mathrm{D}}-\lambda R_{\mathrm{D}}^{2} $ | (15) |
令
| $ a=\frac{\lambda}{G^{2}} $ | (16) |
| $ b=\frac{1-\lambda}{G} $ | (17) |
则式(14)可以写为
| $ p_{\mathrm{D}}=1-b G_{\mathrm{p}}-a G_{\mathrm{p}}^{2} $ | (18) |
由式(17),根据现场数据可拟合求解$a$ 和$b$ 的值。
联立式(15)和式(16),得
| $ a G^{2}+b G-1=0 $ | (19) |
根据一元二次方程求根公式,动态储量$G$ 的表达式为
| $ G=\frac{\sqrt{b^{2}+4 a}-b}{2 a} $ | (20) |
气藏开发早期测压资料较少,压降曲线形态未知。将式(15)两边同乘以$G^{2}$,代入由图 3中$\lambda=0.4288$,由一元二次方程求根公式,得
| $ G=\frac{\left(\sqrt{0.3263+1.7152\left(1-p_{\mathrm{D}}\right)}+0.5712\right) G_{\mathrm{p}}}{2\left(1-p_{\mathrm{D}}\right)} $ | (21) |
由式(21)估算气藏动态储量。根据式(20)和式(21)求得的气藏动态储量,联立式(5)和式(8),气藏侵量的表达式为
| $ W_{\mathrm{e}}=\zeta \omega G B_{\mathrm{gi}}+W_{\mathrm{p}} B_{\mathrm{w}} $ | (22) |
式中:$\zeta$ 为单位换算系数,这里取$10^{4}$。
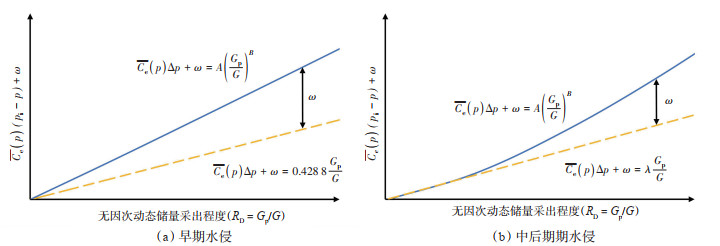
采用图解方法可确定气藏不同水侵方式的$\omega$ 值:若气藏为早期水侵,则$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与$G_{\mathrm{p}} / G$幂指函数拟合关系线位于异常高压无水气藏$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega=0.4288\left(G_{\mathrm{p}} / G\right)$ 线性拟合关系线的上方(图 6a);若气藏为中后期水侵,作$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$与$G_{\mathrm{p}} / G$ 幂指函数拟合关系线的切线,切线的线性方程可近似代表早期无水侵阶段(图 6b)。通过计算2条拟合线的差值,计算$\omega$ 参数。
|
下载原图 图 6 不同水侵方式ω值的计算 Fig. 6 Calculation of ω value for different water invasion |
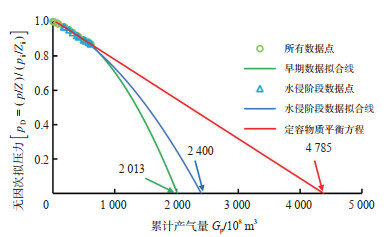
以塔里木盆地克拉2气田为例,验证式(9)、式(14)、式(15)、式(20)和式(22)。该气田原始地层压力为74.41 MPa,容积法地质储量为$2369 \times 10^{8} \mathrm{~m}^{3}$。根据气藏生产历史数据(表 1),分别选择整段和产水阶段数据点绘制$G_{\mathrm{p}}-p_{\mathrm{D}}$ 回归拟合图(图 7)。应用式(15)回归,分别得到拟合关系式$p_{\mathrm{D}}=1-0.000094 G_{\mathrm{p}}- 0.0000007 G_{\mathrm{p}}^{2}$ 和$p_{\mathrm{D}}=1-0.0001767 G_{\mathrm{p}}-0.0000001 G_{\mathrm{p}}^{2}$,相关系数分别为0.9999和0.9970,由式(20)得动态储量分别为$2013 \times 10^{8} \mathrm{~m}^{3}$ 和$2400 \times 10^{8} \mathrm{~m}^{3}$。对比文献[3]和文献[26]计算的克拉2气田的动态储量为($2280 \sim 2291$)$\times 10^{8} \mathrm{~m}^{3}$,由式(15)计算的动态储量是可靠的。而采用定容物质平衡方程计算的动态储量存在极大的计算误差:计算结果为$4785 \times 10^{8} \mathrm{~m}^{3}$。
|
|
下载CSV 表 1 克拉2气田生产历史及计算数据 Table 1 Production history and calculation data of Kela 2 gas field |
|
下载原图 图 7 克拉2气田Gp-pD回归拟合图 Fig. 7 Regression fitting diagram of Gp and pD of Kela 2 gas field |
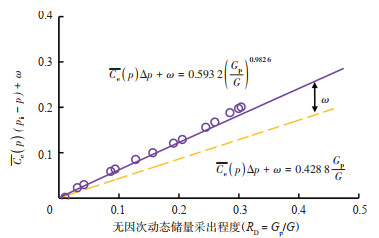
克拉2气田$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 与$G_{\mathrm{p}} / G$ 幂指函数拟合关系式为$\bar{C}_{\mathrm{e}}(p) \Delta p+\omega=0.5932\left(G_{\mathrm{p}} / G\right)^{0.9826}$,相关系数为0.980 6(图 8)。将拟合数值$A$ 和$B$ 代入式(14)得$p_{\mathrm{D}}=1-R_{\mathrm{D}}+0.5932 R_{\mathrm{D}}{ }^{0.9826}-0.5932 R_{\mathrm{D}}{ }^{1.9826}$。在图 8中,由2条曲线的差值确定的$\omega$ 数值,结合由式(22),可确定气藏水侵量。
|
下载原图 图 8 克拉2气田水侵ω值的计算示意图 Fig. 8 Calculation diagram of water invasion ω value in Kela 2 gas field |
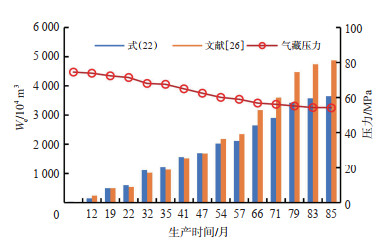
文献[26]中计算的最大水侵量为$4876.89 \times 10^{4} \mathrm{~m}^{3}$,与本次计算的水侵量具有一致性(图 9)。
|
下载原图 图 9 克拉2气田水侵量计算结果对比 Fig. 9 Calculation results comparison of water influx of Kela 2 gas field |
分别利用式(20)和式(22)计算国内5个已开发的异常高压有水气藏(井)的动态储量和水侵量,与调研文献中的动态储量数据和水侵量均较为一致(表 2),由此说明式(20)和式(22)计算的动态储量和水侵量是可靠的。
|
|
下载CSV 表 2 气藏基础参数与动态储量、水侵量计算对比 Table 2 Comparison of basic parameters and calculation results of dynamic reserves and water influx of gas reservoirs |
(1)利用Fetkovich定义的累积有效压缩系数概念,引入动态储量采出程度$G_{\mathrm{p}} / G \text { 与} \bar{C}_{\mathrm{e}}(p) \Delta p+\omega$ 的幂指函数关系,推导出了幂指函数形式的异常高压有水气藏物质平衡方程,并导出了动态储量和水侵量的计算公式,分别建立了早期水侵和中后期水侵的计算方法。
(2)由11个异常高压有水气藏生产数据拟合得到的与幂指函数拟合系数A的值为0.3~0.9,B的值为1~2。A和B的大小反映了气藏水侵发生的早晚:若气藏为早期水侵,则A值越大;若气藏为中后期水侵,则B值越大。
(3)计算并对比6个异常高压有水气藏的生产数据可知,本次新建立的物质平衡方法的计算结果是可靠的。
| [1] |
中华人民共和国国家质量监督检验检疫总局. 天然气藏分类: GB/T 2679-2011[S]. 北京: 中国国家标准化管理委员会, 2011. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China. The classification of natural gas pool: GB/T 2679—2011[S]. Beijing: National Standardization Administration of China, 2011. |
| [2] |
江同文, 王振彪, 宋文宁, 等. 异常高压气田开发. 北京: 石油工业出版社, 2016: 1-24. JIANG Tongwen, WANG Zhenbiao, SONG Wenning, et al. Development of abnormally high pressure gas fields. Beijing: Petroleum Industry Press, 2016: 1-24. |
| [3] |
李明, 陈东, 杨敏, 等. 塔里木某异常高压有水气藏动储量评价过程中的一点认识[R]. 重庆, 第32届全国天然气学术年会, 2020. LI Ming, CHEN Dong, YANG Min, et al. Some insights into the evaluation process of dynamic reserves of an abnormally high pressure water gas reservoir in Tarim[R]. Chongqing, Proceedings of the 32nd National Natural Gas Academic Annual Conference, 2020. |
| [4] |
李明, 唐永亮, 杨敏, 等. 异常高压巨厚气藏水侵模式研究[R]. 西安, 第5届油气田勘探与开发国际会议, 2018. LI Ming, TANG Yongliang, YANG Min, et al. Water invasion mechanisms of abnormal high pressure and thick gas reservoir [R]. Xi'an, Proceedings of the 5th International Conference on Oil and Gas Field Exploration and Development, 2018. |
| [5] |
RAMAGOST B P, FARSHAD F F. P/Z abnormally pressured gas reservoirs[R]. San Antonio, SPE Annual Technical Conference and Exhibition, 1981.
|
| [6] |
BOURGOYNE A T, HAWKINS M F, LAVAQUIAL F P, et al. Shale water as a pressure support mechanism in superpressure reservoirs[R]. Baton Rouge, The Abnormal Subsurface Pressure Symposium, 1972.
|
| [7] |
HAMMERLINDL D J. Predicting gas reserves in abnormally pressured reservoirs[R]. Louisiana, The Fall Meeting of the Society of Petroleum Engineers of AIME, 1971.
|
| [8] |
FETKOVICH M J, REESE D E, WHITSON C H. Application of a general material balance for high-pressure gas reservoirs. SPE Journal, 1998, 3(1): 3-13. DOI:10.2118/22921-PA |
| [9] |
陈元千. 异常高压气藏物质平衡方程式的推导及应用. 石油学报, 1983, 4(1): 45-53. CHEN Yuanqian. Application and derivation of material balance equation for abnormally pressured gas reservoirs. Acta Petrolei Sinica, 1983, 4(1): 45-53. |
| [10] |
陈元千. 确定异常高压气藏地质储量和可采储量的新方法. 新疆石油地质, 2002, 23(6): 516-519. CHEN Yuanqian. New method of determining original gas in place and recoverable reserves for abnormally high pressure gas reservoir. Xinjiang Petroleum Geology, 2002, 23(6): 516-519. DOI:10.3969/j.issn.1001-3873.2002.06.018 |
| [11] |
李传亮. 油藏工程原理. 北京: 石油工业出版, 2005: 115-128. LI Chuangliang. Principles of Reservoir Engineering. Beijing: Petroleum Industry Press, 2005: 115-128. |
| [12] |
ROACH R H. Analyzing geopressured reservoirs-A material balance technique[R]. Houston: Society of Petroleum Engineers, 1981.
|
| [13] |
AMBASTHA A K. A type-curve matching procedure for material balance analysis of production data from geopressured gas reservoirs. Journal of Canadian Petroleum Technology, 1991, 30(5): 61-65. |
| [14] |
GAN R G, BLASINGAME T A. A semianalytical p/z technique for the analysis of reservoir performance from abnormally pressured gas reservoirs[R]. New Orleans, SPE Annual Technical Conference and Exhibition, 2001.
|
| [15] |
GONZALEZ F E, IIK D, BLASINGAME T A. A quadratic cumulative production model for the material balance of an abnormally pressured gas reservoir[R]. Bakersfield, SPE Western Regional and Pacific Section AAPG Joint Meeting, 2008.
|
| [16] |
孙贺东, 王宏宇, 朱松柏, 等. 基于幂函数形式物质平衡方法的高压、超高压气藏储量评价. 天然气工业, 2019, 39(3): 56-64. SUN Hedong, WANG Hongyu, ZHU Songbai, et al. Reserve evaluation of high pressure and ultra high pressure reservoirs with power function material balance method. Natural Gas Industry, 2019, 39(3): 56-64. |
| [17] |
秦正山, 何勇明, 丁洋洋, 等. 边水气藏水侵动态分析方法及水侵主控因素. 岩性油气藏, 2024, 36(4): 178-188. QIN Zhengshan, HE Yongming, DING Yangyang, et al. Water invasion performance and main controlling factors for edgewater gas reservoirs. Lithologic Reservoirs, 2024, 36(4): 178-188. DOI:10.12108/yxyqc.20240416 |
| [18] |
岳世俊, 刘应如, 项燚伟, 等. 一种水侵气藏动态储量和水侵量计算新方法. 岩性油气藏, 2023, 35(5): 153-160. YUE Shijun, LIU Yingru, XIANG Yiwei, et al. A new method for calculating dynamic reserves and water influx of waterinvaded gas reservoirs. Lithologic Reservoirs, 2023, 35(5): 153-160. DOI:10.12108/yxyqc.20230515 |
| [19] |
邓成刚, 李江涛, 柴小颖, 等. 涩北气田弱水驱气藏水侵早期识别方法. 岩性油气藏, 2020, 32(1): 128-134. DENG Chenggang, LI Jiangtao, CHAI Xiaoying, et al. Early identification methods of water invasion in weak water drive gas reservoirs in Sebei gas field, Qaidam Basin. Lithologic Reservoirs, 2020, 32(1): 128-134. DOI:10.12108/yxyqc.20200114 |
| [20] |
李冬梅, 李会会, 朱苏阳, 等. 断溶体油气藏流动物质平衡方法. 岩性油气藏, 2022, 34(1): 154-162. LI Dongmei, LI Huihui, ZHU Suyang, et al. Modified flowing material balance method for fault-karst reservoirs. Lithologic Reservoirs, 2022, 34(1): 154-162. DOI:10.12108/yxyqc.20220116 |
| [21] |
HALL H N. Compressibility of reservoir rocks. Journal of petroleum Technology, 1953, 5(1): 17-19. |
| [22] |
NEWMAN G H. Pore-volume compressibility of consolidated, friable and unconsolidated reservior rocks under hydrostatic loading. Journal of petroleum Technology, 1973, 25(2): 129-135. DOI:10.2118/3835-PA |
| [23] |
LI Chuanliang, CHEN Xiaofan, DU Zhimin. A new relationship of rock compressibility with porosity[R]. Perth, SPE Asia Pacific Oil and Gas Confernce and Exhibition, 2004.
|
| [24] |
陈元千, 邹存友. 三种岩石压缩系数关系的推导与对比. 新疆石油地质, 2012, 33(4): 459-460. CHEN Yuanqian, ZOU Cunyou. Deduction and comparison of relationships among three kinds of rock compressibility factors. Xinjiang Petroleum Geology, 2012, 33(4): 459-460. |
| [25] |
陈元千, 胡建国. 确定异常高压气藏地质储量和有效压缩系数的新方法. 天然气工业, 1993, 13(1): 53-59. CHEN Yuanqian, HU Jianguo. A new method for determining gas in place and effective compressibility in abnormal high pressure gas reservoirs. Natural Gas Industry, 1993, 13(1): 53-59. |
| [26] |
百宗虎. 异常高压整装气藏水侵动态分析方法改进与应用研究[D]. 成都: 西南石油大学, 2012. BAI Zonghu. Improvement and application of dynamic analysis method for water Invasion in abnormal high pressure integrated gas reservoirs[D]. Chengdu: Southwest University of Petroleum, 2012. |
| [27] |
刘思远, 李治平, 陈鹏羽, 等. 异常高压气藏水侵量计算新方法. 特种油气藏, 2017, 24(6): 139-142. LIU Siyuan, LI Zhiping, CHEN Pengyu, et al. A new method for calculating the aquifer influx of abnormal high-pressure gas reservoir. Special Oil & Gas Reservoirs, 2017, 24(6): 139-142. |
| [28] |
马奔腾, 段永刚, 张哲伦, 等. 深层高压有水气藏动态储量图版拟合计算方法. 陕西科技大学学报, 2023, 41(1): 103-109. MA Benteng, DUAN Yonggang, ZHANG Zhelun, et al. Typecurve-based method for dynamic reserve estimate in deep geopressured water-drive gas reservoirs. Journal of Shaanxi University of Science & Technology, 2023, 41(1): 103-109. |
| [29] |
夏静, 谢兴礼, 冀光, 等. 异常高压有水气藏物质平衡方程推导及应用. 石油学报, 2007, 28(3): 96-99. XIA Jing, XIE Xingli, JI Guang, et al. Derivation and application of material balance equation for over-pressured gas reservoir with aquifer. Acta Petrolei Sinica, 2007, 28(3): 96-99. |
| [30] |
罗迪, 张小龙, 谭红, 等. 异常高压水驱气藏物质平衡方程的推导及应用. 西部探矿工程, 2012, 24(6): 74-76. LUO Di, ZHANG Xiaolong, TAN Hong, et al. Derivation and application of material balance equation for abnormally high pressure water drive gas reservoirs. West-China Exploration Engineering, 2012, 24(6): 74-76. |
| [31] |
刘云. 气藏水侵早期识别方法及水侵量计算研究: 以河坝飞三气藏为例[D]. 成都: 成都理工大学, 2011. LIU Yun. Research of methods to identify early water influx of gas reservoirs and calculating water influx rate: Take Heba Feisan Gas Reservoir for example[D]. Chengdu: Chengdu University of Technology, 2011. |
| [32] |
唐建荣, 熊钰, 乐宏, 等. 气藏工程技术. 北京: 石油工程出版社, 2011: 234-235. TANG Jianrong, XIONG Yu, YUE Hong, et al. Gas Reservoir Engineering Technology. Beijing: Petroleum Engineering Press, 2011: 234-235. |
 2025, Vol. 37
2025, Vol. 37



