鄂尔多斯盆地北部伊陕斜坡大牛地气田普遍发育气水分异较差的致密气藏[1],在储层压裂改造波及区域依靠弹性能量生产,气井投产即气水同出。当压力传播至未改造的储层基质时渗透率明显下降,类似于常规油气藏的封闭边界,渗流上出现拟稳态特征,可视为定容气藏类型[2-3]。
气藏工程理论指出,动态储量是现有井网控制条件下的地质储量[4]。对于定容气藏,其物质平衡方程[5]及拟稳态阶段流动物质平衡方程[6-7],在纵坐标为视压力、横坐标为累计产气量的坐标系中为相互平行的线性方程。当绘制视地层压力与累计产气量交会图确定物质平衡方程的斜率,或绘制视流压/视套压/视油压与累计气量交会图确定流动物质平衡方程的斜率后,斜率的倒数为视单位压降产气量,视单位压降产气量与视原始地层压力的乘积即为天然气动态储量。
对于气水同产定容气藏,随水气比增大,采用流动物质平衡方程计算的视单位压降产气量较真实值偏大,导致计算的动态储量逐渐偏大,易造成开发形势误判。从文献调研来看,现有的物质平衡/ 流动物质平衡研究成果可分为2类(均不适应气水同产定容气藏),第1类是针对不考虑地层产水的纯气相定容气藏改进物质平衡/流动物质平衡方程[8-9];第2类是针对考虑储层水侵的水驱气藏改进物质平衡方程[10-12]。针对现有研究成果的不足,首先在纯气相定容气藏物质平衡方程的基础上,引入地层产水因素、岩石骨架压缩因素,建立气水两相物质平衡方程;其次构建基于动态储量、拟压力采气指数双参数约束的迭代求解方法,使建立的气水两相物质平衡方程使用较易获取的井口/井底生产数据即可计算气井动态储量,提高气水同产气井生产潜力评价的可靠性。
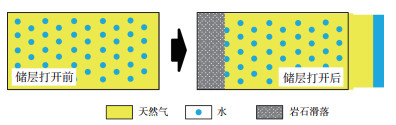
1 气水两相物质平衡方程构建图 1为气水两相分异较差的定容气藏示意图,当储层打开生产后部分天然气(黄色)、地层水(蓝色)排出储层,则在封闭储层内部考虑岩石骨架膨胀占据一定的孔隙体积(灰色),储层内的天然气及地层水再分布充满整个剩余孔隙体积,根据上述产出特征推导建立定容气藏气水两相物质平衡方程。
|
下载原图 图 1 气水同产定容气藏生产示意图 Fig. 1 Sketch map of production style of gas water coproduction volumetric gas reservoirs |
根据物质平衡理论,考虑含水饱和度、累计产水量、岩石骨架压缩因素的影响,得式(1)
| $ \begin{align*} G B_{\mathrm{gi}}+W B_{\mathrm{wi}}= & \left(G-G_{\mathrm{p}}\right) B_{\mathrm{g}}+\left(W-W_{\mathrm{p}}\right) B_{\mathrm{w}}+ \\ & \frac{B_{\mathrm{gi}} G}{S_{\mathrm{gi}}}\left(c_{\mathrm{f}}+S_{\mathrm{wi}} c_{\mathrm{w}}\right)\left(p_{\mathrm{i}}-p\right) \end{align*} $ | (1) |
式中:$G$ 为天然气动态储量,$\mathrm{m}^{3}; W$ 为地层水动态储量,同理于天然气动态储量,$\mathrm{m}^{3}; G_{\mathrm{p}}$ 为累计产气量,$\mathrm{m}^{3}; W_{\mathrm{p}}$ 为累计水产量,$\mathrm{m}^{3}; p_{\mathrm{i}}$ 为原始地层压力,MPa;$p$ 为累计产气量对应的地层压力,$\mathrm{MPa}; ~ B_{\mathrm{gi}}$ 为原始地层压力下天然气体积系数;$B_{\mathrm{g}}$ 为地层压力下天然气体积系数;$B_{\mathrm{wi}}$ 为原始地层压力下水体积系数;$B_{\mathrm{w}}$ 为地层压力下水体积系数;$S_{\mathrm{gi}}$ 为原始地层压力下含气饱和度;$S_{\mathrm{wi}}$ 为原始地层压力下含水饱和度;$C_{\mathrm{f}}$ 为岩石压缩系数,$\mathrm{MPa}^{-1}; C_{\mathrm{w}}$ 为水压缩系数,$\mathrm{MPa}^{-1}$。
油层物理学指出[13],在储层温度不变的情况下,地层压力由 0 增至 30 MPa,水体积系数为 0.3%~0.8%。具体到大牛地气田(储层温度为 93 ℃,最高地层压力小于 30 MPa),地层压力由 0 增至 30 MPa,水体积系数由 1.035 降至 1.031,降幅为 0.4%,可近似认为水体积系数不随压力变化。因此,令 Bwi =Bw,并将天然气体积系数[4]表达式(2)代入式(1),变形后得到标准型气水两相物质平衡方程
| $ B_{\mathrm{gi}}=\frac{p_{\mathrm{SC}} Z_{\mathrm{i}} T}{p_{\mathrm{i}} T_{\mathrm{SC}}}, B_{\mathrm{g}}=\frac{p_{\mathrm{SC}} Z T}{p T_{\mathrm{SC}}} $ | (2) |
| $ \begin{gather*} \frac{p}{Z}\left[S_{\mathrm{gi}}-\left(c_{\mathrm{f}}+S_{\mathrm{wi}} c_{\mathrm{w}}\right)\left(p_{\mathrm{i}}-p\right)+\frac{W_{\mathrm{p}} B_{\mathrm{w}} S_{\mathrm{gi}}}{G B_{\mathrm{gi}}}\right]= \\ \frac{p_{\mathrm{i}}}{Z_{\mathrm{i}}}\left(1-\frac{G_{\mathrm{p}}}{G}\right) S_{\mathrm{gi}} \end{gather*} $ | (3) |
式中:$p_{\mathrm{sc}}$ 为标准状态下大气压力,$\mathrm{MPa}; T_{\mathrm{sc}}$ 为标准状态下温度,${ }^{\circ} \mathrm{C}; T$ 为储层温度,${ }^{\circ} \mathrm{C}; ~ Z_{\mathrm{i}}$ 为原始地层压力下天然气压缩因子;$Z$ 为地层压力下天然气压缩因子。
1.2 构建简化型气水两相物质平衡方程定义等效压缩因子$Z_{e}$,表达式见式(4)。当储层未打开时,$p=p_{\mathrm{i}}, W_{\mathrm{p}}=0$,得到原始地层压力下的等效压缩因子$Z_{\mathrm{e} \mathrm{i}}$。将式(4)代入式(3),得到简化型气水两相物质平衡方程式(5)。
| $ \begin{gathered} Z_{\mathrm{e}}=\frac{Z}{S_{\mathrm{gi}}-\left(c_{\mathrm{f}}+S_{\mathrm{wi}} c_{\mathrm{w}}\right)\left(p_{\mathrm{i}}-p\right)+\frac{W_{\mathrm{p}} B_{\mathrm{w}} S_{\mathrm{gi}}}{G B_{\mathrm{gi}}}}, \\ Z_{\mathrm{ei}}=\frac{Z}{S_{\mathrm{gi}}} \end{gathered} $ | (4) |
| $ \frac{p}{Z_{\mathrm{e}}}=\left(1-\frac{G_{\mathrm{p}}}{G}\right) \frac{p_{\mathrm{i}}}{Z_{\mathrm{ei}}} $ | (5) |
由于定义的等效压缩因子中包含动态储量,因此难以像流动物质平衡方程一样直接求解。通过引入拟压力采气指数,构建基于动态储量、拟压力采气指数双参数约束的迭代求解方法。
2.1 设定双参数迭代求解初始值分别设定动态储量G、拟压力采气指数PI的值。
拟压力采气指数(简称采气指数),与油藏中的采液指数[14-15]定义类似,是指单位生产压差下的日产气量[16],其方程见式(6)。气藏中采用拟压力代替真实压力以消除天然气性质变化对压力的影响,因此拟压力可以理解为等效液体压力,且拟压力采气指数在拟稳态阶段接近常数[16]。气水两相拟压力计算方程见式(7)[17-19]。
| $ P I=\frac{q_{\mathrm{g}}}{\varphi_{\mathrm{p}}-\varphi_{\mathrm{wf}}} $ | (6) |
| $ \varphi_{\mathrm{p}}=\int_{0}^{p}\left(\frac{K_{\mathrm{rg}}}{\mu_{\mathrm{g}}} \rho_{\mathrm{g}}+\frac{K_{\mathrm{rw}}}{\mu_{\mathrm{w}}} \rho_{\mathrm{w}}\right) d p $ | (7) |
式中:$P I$ 为采气指数,$\left(\mathrm{m}^{3} / \mathrm{d}\right) \cdot\left(\mathrm{mPa} \cdot \mathrm{s} \cdot \mathrm{m}^{3}\right) /(\mathrm{kg} \cdot \mathrm{MPa})$;$q_{\mathrm{g}}$ 为日产气量,$\mathrm{m}^{3}; K_{\mathrm{rg}}, K_{\mathrm{rw}}$ 分别为气相、水相相对渗透率;$\mu_{\mathrm{g}}, \mu_{\mathrm{w}}$ 分别为气相、水相黏度,$\mathrm{mPa} \cdot \mathrm{s}; \rho_{\mathrm{g}}$,$\rho_{\mathrm{w}}$ 分别为气相、水相密度,$\mathrm{kg} / \mathrm{m}^{3}; q_{\mathrm{g}}$ 为日产气量,$\mathrm{m}^{3}; \varphi_{\mathrm{p}}, \varphi_{\mathrm{wf}}$ 分别为地层压力、井底流压的拟压力,$\mathrm{kg} \cdot \mathrm{MPa} /\left(\mathrm{mPa} \cdot \mathrm{s} \cdot \mathrm{m}^{3}\right)$。
2.2 求解方程所需的基础参数收集并给出方程所需的基础参数原始含气饱和度$S_{\mathrm{gi}}$、含水饱和度$S_{\mathrm{wi}}$、岩石压缩系数$c_{\mathrm{f}}$,根据PVT方程绘制天然气压缩因子$Z$、天然气体积系数$B_{\mathrm{g}}$、水体积系数$B_{\mathrm{w}}$、水压缩系数$c_{\mathrm{w}}$ 与压力$p$ 的对映关系表;同时收集不同累计产气量$G_{\mathrm{p}}$ 对应的累计产水量$W_{\mathrm{p}}$、日产气量$q_{\mathrm{g}}$、实测或折算流压数据$p_{\mathrm{wf}}$。文献调研显示,气井流压折算方法已较为成熟[20-22],缺少实测流压时亦可通过折算流压开展计算。
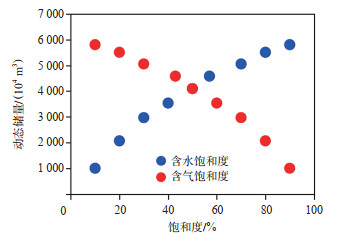
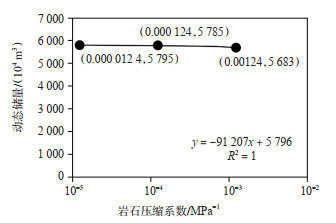
由于原始含气饱和度$S_{\mathrm{gi}}$、原始含水饱和度$S_{\mathrm{wi}}$ 由测井解释获得,岩石压缩系数$c_{\mathrm{f}}$ 由岩心测试获得,需要评价方程对上述参数的敏感性,以指导参数获取。由图 2可见,随着含水饱和度由$10 \%$ 增至$90 \%$,气井动态储量由$5804 \times 10^{4} \mathrm{~m}^{3}$ 降至$1013 \times 10^{4} \mathrm{~m}^{3}$,即方程对$S_{\mathrm{gi}}, S_{\mathrm{wi}}$ 较为敏感,需要测井提供准确的解释成果。由图 3可见,以气田平均岩石压缩系数$1.24 \times 10^{-4} \mathrm{MPa}^{-1}$ 为基准,岩石压缩系数每增大一个数量级,相应的动态储量降低$100 \times 10^{4} \mathrm{~m}^{3}$,相当于降低$1.7 \%$,即方程对$c_{\mathrm{f}}$ 不敏感,在缺少实测数据时可采用气田平均数据。
|
下载原图 图 2 饱和度与动态储量交会图 Fig. 2 Crossplot of saturation and dynamic reserves |
|
下载原图 图 3 岩石压缩系数与动态储量交会图 Fig. 3 Crossplot of stone compression coefficient and dynamic reserves |
将设定的动态储量$G$ 值带人式(3),反算出一组不同累计产气量($G_{\mathrm{p} 1}, G_{\mathrm{p} 2}, G_{\mathrm{p} 3}, \ldots, G_{\mathrm{pn}}$)对应的地层压力($p_{1}, p_{2}, p_{3}, \ldots, p_{\mathrm{n}}$),进一步根据式(4)计算地层压力对应的等效压缩因子,从而计算出一组视地层压力($p_{1} / Z_{\mathrm{e} 1}, p_{2} / Z_{\mathrm{e} 2}, p_{3} / Z_{\mathrm{e} 3}, \ldots, p_{\mathrm{n}} / Z_{\mathrm{en}}$),在横坐标为累计产气量、纵坐标为视地层压力的坐标系中绘制出该组数据的散点线,定义为"设定动态储量反算的物质平衡线"。
2.3.2 动态储量计算的采气指数线根据式(7),将2.3.1中计算的地层压力($p_{1}, p_{2}$,$\left.p_{3}, \ldots, p_{\mathrm{n}}\right)$ 转为为拟压力$\left(\varphi_{\mathrm{p} 1}, \varphi_{\mathrm{p} 2}, \varphi_{\mathrm{p} 3}, \ldots, \varphi_{\mathrm{pn}}\right)$,将收集的不同累计产气量对应的流压($p_{\mathrm{wf} 1}, p_{\mathrm{wf} 2}, p_{\mathrm{wf} 3}, \ldots, p_{\mathrm{wfn}}$)转换为拟压力($\varphi_{\mathrm{wfl}}, \varphi_{\mathrm{wf} 2}, \varphi_{\mathrm{wf} 3}, \ldots, \varphi_{\mathrm{wfn}}$),并由式(6)计算出不同累计产气量对应的拟压力采气指数($P I_{1}$,$\left.{PI}_{2}, {PI}_{3}, \ldots, {PI}_{\mathrm{n}}\right)$,在横坐标为累计产气量、纵坐标为采气指数的坐标系中绘制出该组数据的散点线,定义为"设定动态储量计算的采气指数线"。
2.3.3 采气指数反算的物质平衡线将设定的拟压力采气指数$P I$ 值带入式(6),根据2.3.2中的流压拟压力($\varphi_{\mathrm{wfl}}, \varphi_{\mathrm{wf} 2}, \varphi_{\mathrm{wf} 3}, \ldots, \varphi_{\mathrm{wfn}}$)、对应的日产气量$\left(q_{\mathrm{g} 1}, q_{\mathrm{g} 2}, q_{\mathrm{g} 3}, \ldots, q_{\mathrm{gn}}\right)$ 反算出一组新的地层压力拟压力$\left(\varphi_{\mathrm{p} 1}{ }^{*}, \varphi_{\mathrm{p} 2}{ }^{*}, \varphi_{\mathrm{p} 3}{ }^{*}, \ldots, \varphi_{\mathrm{pn}}{ }^{*}\right)$,进一步根据式(7)、式(4)计算出对应的视地层压力($p_{1} / Z_{\mathrm{e} 1}{ }^{*}, p_{2} / Z_{\mathrm{e} 2}{ }^{*}$,$\left.p_{3} / Z_{\mathrm{e} 3}{ }^{*}, \ldots, p_{\mathrm{n}} / Z_{\mathrm{en}}{ }^{*}\right)$,同样在横坐标为累计产气量、纵坐标为视地层压力的坐标系中绘制出该组数据的散点线,定义为"设定采气指数反算的物质平衡线"。
2.3.4 采气指数水平线由于设定的拟压力采气指数PI值为定值,不随累计产气量变化,其在横坐标为累计产气量、纵坐标为采气指数的坐标系中为一条水平线,定义为“设定的采气指数水平线”
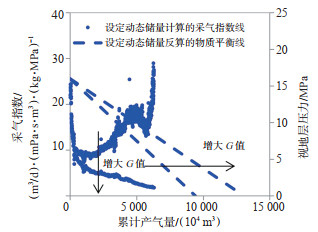
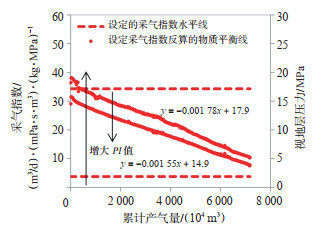
2.4 调整初始值使同类曲线重合/平行迭代求解结合式(5)、式(6)来看,构建的4条曲线有2个特点:第1个特点是调整G的值,只改变“设定动态储量反算的物质平衡线的斜率和设定动态储量计算的采气指数线的斜率,但截距不变(图 4);第2个特点是调整PI的值,主要改变设定的采气指数水平线的截距和设定的采气指数反算的物质平衡线的截距,斜率仅小幅度改变(图 5中,PI值增大9.4倍,设定采气指数反算的物质平衡线的斜率增加17%)。这2个特点可以理解为:设定PI值构建的2条线的斜率近似不变,从而将G值限制在较小的范围内;设定G值构建的2条线的截距不变,从而将PI值限制在较小的范围内。考虑到实际生产数据的波动,可以对G值和PI值进行微调得到最优解,但不会出现G值与PI值互补的多解性。
|
下载原图 图 4 G值对物质平衡线、采气指数线的影响 Fig. 4 Influence of G-value on material balance line and gas recovery index line |
|
下载原图 图 5 PI值对物质平衡线、采气指数线的影响 Fig. 5 Influence of PI-value on material balance line and gas recovery index line |
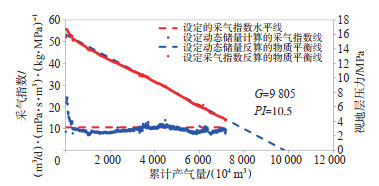
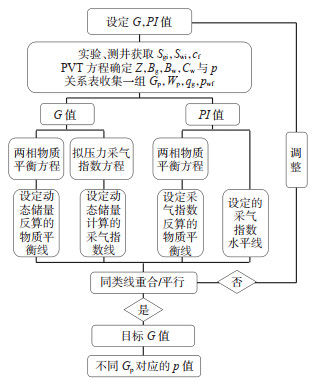
在实际迭代求解中,一是调整动态储量G的值,目标是使“设定动态储量计算的采气指数线”尽可能接近水平状态,同时使“设定动态储量反算的物质平衡线”与斜率近似不变的“设定采气指数反算的物质平衡线”尽可能接近相互平行状态。二是调整采气指数PI的值,目标是使“设定采气指数反算的物质平衡线”与截距不变的“设定动态储量反算的物质平衡线”尽可能接近重合状态,同时使“设定的采气指数水平线”与“设定动态储量计算的采气指数线”尽可能接近重合状态。当4条曲线之间的关系接近理想状态时,即得到动态储量G的最优解(图 6),并进一步根据式(3)计算出不同累计产气量对应的地层压力,整个迭代计算流程如图 7所示。
|
下载原图 图 6 气水两相物质平衡方程求解图版 Fig. 6 Calculation chart of gas-water two-phase material balance equation |
|
下载原图 图 7 动态储量迭代计算流程图 Fig. 7 Flowchart for iterative calculation of dynamic reserves |
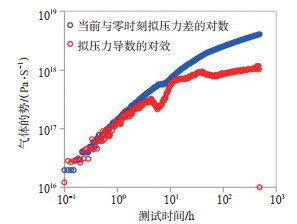
选取压恢试井解释地层压力,以及计算的动态储量作为方程准确性验证基准值。以大牛地气田A井为例,该井2013年7月份投产生产至2024年6月,原始地层压力为22.663 MPa,原始含气饱和度为57%、原始含水饱和度为43%、累产气为3 864×104 m3、累产水为13 153 m3,全历史水气比为3.4 m3/104 m3。该井2017年10月、2021年7月完成2次压恢试井(图 8,图 9),全历史完成24次流压测试,依托上述数据对气水两相物质平衡方程进行验证。
|
下载原图 图 8 A井2017年压恢试井双对数曲线 Fig. 8 Double logarithmic curve of pressure recovery well testing of A well in 2017 |
|
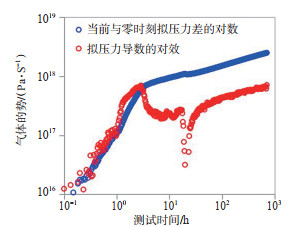
下载原图 图 9 A井2021年压恢试井双对数曲线 Fig. 9 Double logarithmic curve of pressure recovery well testing of A well in 2021 |
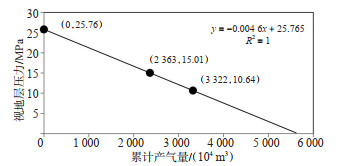
A井2017年10月累产气为2 363×104 m3、累产水为6 145 m3时解释的地层压力为13.2 MPa(视地层压力为15.01 MPa);2021年7月累产气为3 322× 104 m3、累产水为10 093 m3时解释的地层压力为9.6 MPa(视地层压力为10.64 MPa),采用物质平衡方程(图 10)计算A井动态储量为5 601×104 m3。
|
下载原图 图 10 物质平衡方程计算A井动态储量 Fig. 10 Dynamic reserves of well A caculated with material balance equation |
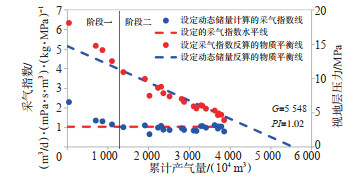
依托A井全历史24井次流压数据,绘制A井气水两相物质平衡图版。由图 11可见,A井可分为2个阶段,其中阶段二斜率(斜率倒数即为视单位压降产气量)明显小于阶段一,评价认为阶段二(累产气1 325×104 m3)A井进入拟稳态阶段,因此主要拟合阶段二的4条曲线。计算A井动态储量为5 548×104 m3,对应的2017年10月地层压力为13.1 MPa,2021年7月地层压力为9.4 MPa。与验证基准值相比,2017年10月地层压力计算误差为-1%,2021年7月地层压力计算误差为-2%,动态储量计算误差为-4%,整体误差较小。
|
下载原图 图 11 流动物质平衡方程计算A井动态储量 Fig. 11 Dynamic reserves of well A caculated with flowing material balance equation |
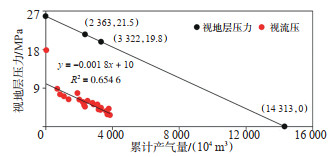
依托A井全历史24井次流压数据,绘制A井流动物质平衡图版(图 12),评价累计产气为866×104 m3后进入拟稳态阶段,计算动态储量为14 313×104 m3,对应的2017年10月地层压力为18.9 MPa(视地层压力21.5 MPa),2021年7月地层压力为17.5 MPa(视地层压力19.8 MPa)。与验证基准值相比,2017年10月地层压力计算误差为43%,2021年7月地层压力计算误差为82%,动态储量计算误差为146%,误差明显偏大。
|
下载原图 图 12 流动物质平衡方程计算A井动态储量 Fig. 12 Dynamic reserves of well A caculated with flowing material balance equation |
对比可见,A井采用气水两相物质平衡方程计算结果与验证基准值相近,流动物质平衡方程计算结果明显偏大,相同的情况在大牛地气田B井、C井同样出现(表 1)。统计来看,采用气水两相物质平衡方程计算的地层压力平均绝对误差为5.2%,动态储量平均绝对误差为5.0%;采用流动物质平衡方程计算的地层压力平均绝对误差为53%,动态储量平均绝对误差为111%。
|
|
下载CSV 表 1 不同方法计算动态储量及地层压力对比表 Table 1 Statistics of dynamic reserves and formation pressure caculated by different methods |
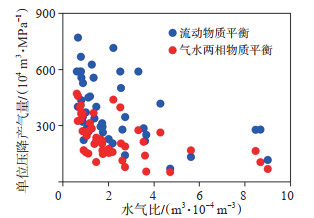
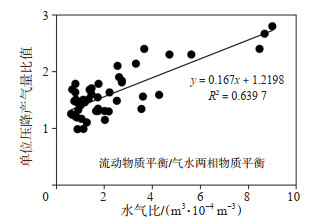
研究中挑选大牛地气田46口不同水气比气井,同一口气井分别采用气水两相物质平衡方程、流动物质平衡方程计算单位压降产气量以对比差异。由图 13可见,水气比越大计算的单位压降产气量越小(即动态储量越小),但流动物质平衡方程计算的单位压降产气量整体偏高;由图 14可见,将同一口气井2种方法计算的单位压降产气量作比值,水气比越大,二者差异越大。
|
下载原图 图 13 2种方法计算单位压降产气量差异图 Fig. 13 Difference of gas production under unit pressure drop calculated by flowing material balance equation and gas-water two-phase material balance equation |
|
下载原图 图 14 2种方法计算单位压降产气量比值图 Fig. 14 Ratio of gas production under unit pressure drop calculated by flowing material balance equation and gas-water two-phase material balance equation |
(1)考虑储层含水饱和度、累计产水量、岩石骨架膨胀综合影响,推导建立了定容气藏气水两相物质平衡方程,并构建基于动态储量、拟压力采气指数双参数约束的迭代求解方法,依托较易获取的井口/井底生产数据即可计算气井动态储量。
(2)经压恢试井成果验证,气水两相物质平衡方程计算地层压力平均绝对误差为5.2%,动态储量平均绝对误差为5.0%,流动物质平衡方程计算的平均绝对误差分别为53% 和111%,对比来看气水两相物质平衡方程更适用于气水同产定容气藏。
(3)气井动态储量随着水气比增大而减小,且水气比越大,分别采用气水两相物质平衡方程、流动物质平衡方程计算的动态储量差异越大。
| [1] |
李仲东, 郝蜀民, 李良, 等. 鄂尔多斯盆地上古生界气藏与深盆气藏特征对比. 石油与天然气地质, 2009, 30(2): 149-155. LI Zhongdong, HAO Shumin, LI Liang, et al. Comparison between the Upper Paleozoic gas reservoirs in Ordos Basin and deep basin gas reservoirs. Oil & Gas Geology, 2009, 30(2): 149-155. |
| [2] |
蔡振华, 王文升, 李昀昀, 等. 致密砂岩气藏多段压裂水平气井动态控制储量计算方法. 长江大学学报(自然科学版), 2017, 14(1): 31-35. CAI Zhenhua, WANG Wensheng, LI Yunyun, et al. A method for calculating dynamically controlled reserves of multi-stage fractured horizontal wells in tight sandstone gas reservoirs. Journal of Yangtze University(Natural Science Edition), 2017, 14(1): 31-35. |
| [3] |
邓江明, 张茂林, 梅海燕. 低渗气藏压敏性对合理产能影响研究. 西南石油大学学报(自然科学版), 2007, 29(4): 107-109. DENG Jiangming, ZHANG Maolin, MEI Haiyan. The influence of reasonable production on pressure sensitivity in low permeability gas reservoir. Journal of Southwest Petroleum University(Science & Technology Edition), 2007, 29(4): 107-109. |
| [4] |
李士伦. 天然气工程. 北京: 石油工业出版社, 2008. LI Shilun. Gas reservoir engineering. Beijing: Petroleum Industry Press, 2008. |
| [5] |
史玉成, 陈明强, 张审琴, 等. 低渗透气田单井控制储量计算的流动单元方法研究. 岩性油气藏, 2007, 19(4): 106-110. SHI Yucheng, CHEN Mingqiang, ZHANG Shenqin, et al. Flow unit method for calculation of single well controlled reserves in low permeability gas field. Lithologic Reservoirs, 2007, 19(4): 106-110. DOI:10.3969/j.issn.1673-8926.2007.04.019 |
| [6] |
钟海全, 周俊杰, 李颖川, 等. 流动物质平衡法计算低渗透气藏单井动态储量. 岩性油气藏, 2012, 24(3): 108-111. ZHONG Haiquan, ZHOU Junjie, LI Yingchuan, et al. Dynamic reserve calculation of single well of low permeability gas reservoir based on flowing material balance method. Lithologic Reservoirs, 2012, 24(3): 108-111. DOI:10.3969/j.issn.1673-8926.2012.03.021 |
| [7] |
刘尧文, 张茂林, 刘常旭, 等. 利用流动物质平衡确定低渗气藏单井控制储量. 天然气勘探与开发, 2013, 36(2): 41-43. LIU Yaowen, ZHANG Maolin, LIU Changxu, et al. Flowing material balance method to determine controlled reserves of single well in low permeability gas reservoirs. Natural Gas Exploration and Development, 2013, 36(2): 41-43. |
| [8] |
周声才, 周俊杰, 沈大富, 等. 低渗气藏单井动态储量计算方法研究. 重庆科技学院学报(自然科学版), 2013, 15(2): 10-13. ZHOU Shengcai, ZHOU Junjie, SHEN Dafu, et al. On calculation method of dynamic reserve of low permeability reservoir single well. Journal of Chongqing University of Science and Technology(Natural Science Edition), 2013, 15(2): 10-13. |
| [9] |
王永科, 白慧芳, 王凯, 等. 定容封闭气藏定产气井动态储量计算新方法. 中国科技论文, 2021, 16(1): 91-96. WANG Yongke, BAI Huifang, WANG Kai, et al. A new method for calculating the dynamic reserves of fixed production gas wells in closed constant volume gas reservoir. China Sciencepaper, 2021, 16(1): 91-96. |
| [10] |
岳世俊, 刘应如, 项燚伟, 等. 一种水侵气藏动态储量和水侵量计算新方法. 岩性油气藏, 2023, 35(5): 153-160. YUE Shijun, LIU Yingru, XIANG Yiwei, et al. A new method for calculating dynamic reserves and water influx of water invaded gas reservoirs. Lithologic Reservoirs, 2023, 35(5): 153-160. DOI:10.12108/yxyqc.20230515 |
| [11] |
陈恒, 杜建芬, 郭平, 等. 裂缝型凝析气藏的动态储量和水侵量计算研究. 岩性油气藏, 2012, 24(1): 117-120. CHEN Heng, DU Jianfen, GUO Ping, et al. Study on calculation of dynamic reserves and water influx in fractured condensate gas reservoir. Lithologic Reservoirs, 2012, 24(1): 117-120. DOI:10.3969/j.issn.1673-8926.2012.01.023 |
| [12] |
于清艳, 牟珍宝, 刘鹏程, 等. 含边底水气藏的水侵量计算方法. 新疆石油地质, 2017, 38(5): 586-591. YU Qingyan, MU Zhenbao, LIU Pengcheng, et al. Calculation methods of water influx in gas reservoirs with aquifers. Xinjiang Petroleum Geology, 2017, 38(5): 586-591. |
| [13] |
杨胜来, 魏俊之. 油层物理学. 北京: 石油工业出版社, 2008. YANG Shenglai, WEI Junzhi. Fundamentals of petrophysics. Beijing: Petroleum Industry Press, 2008. |
| [14] |
张琪. 采油工程原理与设计. 东营: 中国石油大学出版社, 2006. ZHANG Qi. Principle and design of oil production engineering. Dongying: China University of Petroleum Press, 2006. |
| [15] |
何岩峰, 吴晓东, 王云川, 等. 采液指数预测新方法. 石油钻采工艺, 2008, 30(3): 60-62. HE Yanfeng, WU Xiaodong, WANG Yunchuan, et al. New predicting method for fluid productivity indexs. Oil Drilling & Production Technology, 2008, 30(3): 60-62. |
| [16] |
鹿克峰, 苏畅, 程超逸. 一种评价封闭气藏采气指数、动储量及井间连通性的简便方法. 中国海上油气, 2023, 35(4): 86-93. LU Kefeng, SU Chang, CHENG Chaoyi. A simple method for evaluating gas production index, dynamic reserves and interwell connectivity of closed gas reservoirs. China Offshore Oil and Gas, 2023, 35(4): 86-93. |
| [17] |
李晓平, 赵必荣. 气水两相流井产能分析方法研究. 油气井测试, 2001, 10(4): 8-10. LI Xiaoping, ZHAO Birong. Study of productivity analysis method for gas-water well. Well Testing, 2001, 10(4): 8-10. |
| [18] |
孙恩慧, 李晓平, 王伟东. 低渗透气藏气水两相流井产能分析方法研究. 岩性油气藏, 2012, 24(6): 121-124. SUN Enhui, LI Xiaoping, WANG Weidong. Productivity analysis method of water and gas two-phase flow well in low permeability gas reservoirs. Lithologic Reservoirs, 2012, 24(6): 121-124. DOI:10.3969/j.issn.1673-8926.2012.06.022 |
| [19] |
袁淋, 李晓平, 刘建军. 低渗透气藏气水同产压裂水平井产能计算方法. 岩性油气藏, 2016, 28(4): 88-94. YUAN Lin, LI Xiaoping, LIU Jianjun. Productivity calculation method of fractured horizontal wells with gas-water two-phase in low permeability gas reservoirs. Lithologic Reservoirs, 2016, 28(4): 88-94. DOI:10.3969/j.issn.1673-8926.2016.04.012 |
| [20] |
王锦昌, 赵润冬. 高压集输气井井筒积液量与流压计算方法. 西安石油大学学报(自然科学版), 2024, 39(3): 50-57. WANG Jinchang, ZHAO Rundong. Calculation method for wellbore liquid volume and bottom-hole flowing pressure of high-pressure gathering and transmission natural gas wells. Journal of Xi'an Shiyou University(Natural Science Edition), 2024, 39(3): 50-57. |
| [21] |
孟红霞, 徐悦新, 陈德春, 等. 气井井筒积液高度计算模型研究. 复杂油气藏, 2019, 12(1): 81-85. MENG Hongxia, XU Yuexin, CHEN Dechun, et al. Calculation model for height of liquid loading in gas wellbore. Complex Hydrocarbon Reservoirs, 2019, 12(1): 81-85. |
| [22] |
罗程程, 靳悦, 刘永辉, 等. 气井零液流量流动模拟实验及模型应用研究. 钻采工艺, 2022, 45(4): 81-86. LUO Chengcheng, JIN Yue, LIU Yonghui, et al. Experimental and modeling investigation on zero net-liquid flow in gas wells. Drilling & Production Technology, 2022, 45(4): 81-86. |
 2025, Vol. 37
2025, Vol. 37



