随钻方位伽马测井已经成为国外大斜度井和水平井随钻过程中的必测项目，同时配套形成了商业化应用的成像处理软件^[1-2]。国内随钻方位伽马测井仪器目前还处于研制试验阶段，尚未形成商业化应用产品，相关配套的成像处理软件大多都借鉴和应用斯伦贝谢GeoFrame、阿特拉斯eXpress以及中油测井LEAD等第三方软件平台。

由于受到钻井过程中井下测量信号传输速率的限制，同一深度点上一般实时上传最多不超过8个方位的伽马测量值，这种实时数据处理方式与传统的针对电缆声电成像测井处理过程和处理方法明显不同^[3-4]，若不加以改进则无法直接应用。针对随钻伽马测井存在井周测量数据少、不同扇区数据相关性高的特点，借助周期样条插值实现测量数据360°全方位插值处理，从而满足高分辨率图像的精度要求；为了更清晰地反映岩石内部组构特征，通过优选符合地质图像特点的特定色谱和颜色刻度标定方法，对插值后的伽马数据进行全井段或局部井段颜色映射处理，再把颜色数据按照坐标位置显示出来，从而完成随钻伽马成像测井图像的绘制。通过在薄油藏等复杂油藏中的地质导向应用，及时分辨不同岩性的界面，确定进入储层的最佳时机，为进一步开发低品质油气藏、难动用油气藏提供强有力的技术支撑。

传统的随钻伽马测量仪是在随钻测量工具内安装自然伽马传感器，通过伽马传感器内的计数管来获取其周围岩层中放射出的γ射线，然后进行API刻度后传输至地面，进而判断地层的平均伽马值^[5]。由于没有方向性，当测量参数反映出轨迹已经不在目标层时，不能确定钻头从上面出层，还是从下面出层，因此也无法落实重返目标层的措施。随钻多扇区方位伽马测量技术是近年来发展起来的一种新型随钻测量技术，要实现多扇区的方位伽马测量，甚至方位伽马成像，不仅要对仪器进行伽马API单位刻度，还需要对仪器的方位响应进行刻度，才能准确得出仪器对于每个扇区方位地层的响应贡献。

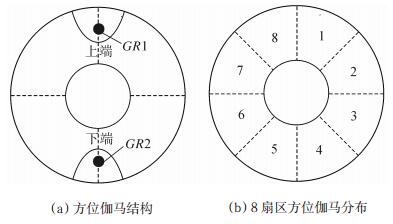
随钻方位伽马测量仪通常将一个或多个伽马传感器对称安装于钻铤表面，用以记录来自其对应地层的伽马射线。钻具旋转中，利用井下扇区方位测量系统分时、分区累计来自各对应地层的自然伽马，经过实体刻度及修正技术得到国际通用的API数据，用于表征对应地层的泥质含量。在方位伽马及成像伽马仪器开发中，利用钻铤本体充当伽马测量的天然屏蔽体，为实现方位伽马测量提供了可能。图 1(a)是2个伽马传感器对称安装时钻铤表面的结构，用以记录来自上、下2个方位的地层伽马射线，根据需要还可以将扇区配置为4，8或16个方位进行实时测量。图 1(b)是8扇区方位伽马测量分布示意图，不仅可以实现常规自然伽马应用，还可以对地层进行伽马成像，拾取地层倾角和分析构造，进而更好地指导地质导向和地层评价^[6-7]。

图 1

Fig. 1

下载eps/tif图 图 1 方位伽马结构及测量扇区分布示意图 Fig. 1 Structure of azimuthal gamma and distribution of measurement sectors

随钻方位伽马数据实现成像，首先需要将测量的伽马值进行插值处理，同时根据不同的色度标定方法预定义成像色谱，再将伽马值按照一定的规则刻度成对应颜色的色标数据 (一般亮色代表低伽马值，暗色代表高伽马值)，最后把伽马颜色数据按坐标位置显示出来，即可生成随钻伽马测井图像。通过后续计算机图像学的进一步处理，可以提高成像测井图像解释结果的精度，从而满足不同地层地质分析的要求^[8-9]。

把每个深度点上所测量的一组伽马数据 (以8条曲线为例进行说明) 作为一个数据区间，由于测量的伽马数据点较少，要生成沿井周360°的伽马图像，必须进行插值才能实现较好的成像效果，本文采用的插值方法是三次样条函数插值^[10-12]，该插值方法既能保证插值结果包含所测量的方位伽马真值，又能保证在数据区间上一阶导数平滑和二阶导数连续，从而使得每个深度点上的测量数据都具有较好的相关性并且插值结果比较光滑。通过插值方法处理，可以将仪器测量的8个方位伽马数据展开为沿井周360°连续变化的伽马图像，从而直观地表现出地层界面不同方位的岩性变化情况。

按照三次样条函数的定义，设有n+1个点B_i (x_i，y_i)(i=0，1，…，n)，且有x₀ < x₁ < … < x_n，若函数S(x) 满足条件：①S(x_i)=y_i(i=0，1，…，n)；②在区间[x₀，x_n]，S(x) 具有二阶连续导数；③在每个子区间[x_i-1，x_i]，S(x) 是x的三次多项式，则称S(x) 为关于节点B₀，B₁，B₂，…，B_n的三次样条函数。由于根据三次样条函数插值条件与样条条件导出的求解方程组中只有n-1个条件方程，却包含有n + 1个待定系数，因此还缺少2个方程。这2个方程通常利用端点处的以下3种边界条件得到：①利用端点处一阶导数S'(x₀)=y'₀，S'(x_n)=y'_n；②利用端点处二阶导数M₀=y"₀，M_n=y"_n；③满足周期条件y₀=y_n，y'₀=y'_n，y"₀=y"_n。由于方位伽马测量数据是井周0~360°方位角对应的扇区数据，因此采用第3类周期样条插值函数来进行计算。

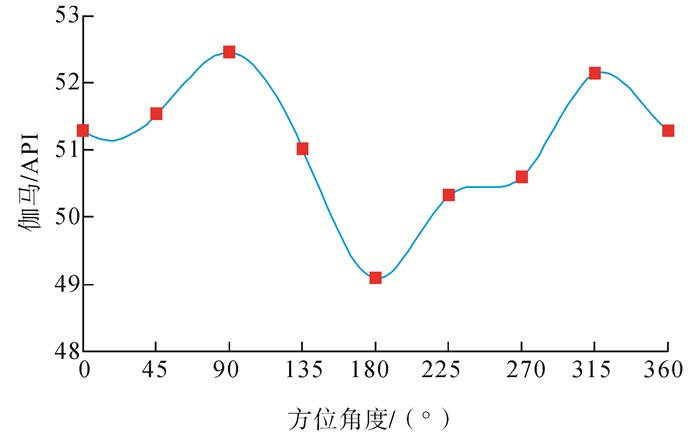
将8扇区伽马测量值与对应方位角构成节点B_i(r_i，θ_i)(i=0，1，…，n)，并且r_n=r₀，θ_n=θ₀+2π，其中r_i为节点B_i的伽马测量值，θ_i为节点B_i对应的方位角，则此n+1个节点满足θ₀ < θ₁ < … < θ_n，再按周期条件补充方程即可实现不同方位插值点处伽马值的计算。利用节点 (r₀，θ₀)，(r₁，θ₁)，…，(r_n，θ_n)，并且补充方程r'₀=r'_n，r"₀=r"_n，(即M₀=M_n)，利用周期边界条件的三次样条函数插值就可以分段求出样条函数r(θ) 值，即插值点处伽马值。按照以上插值算法进行编程，将每一深度点的样本点数、样本值及插值点数作为输入参数，输出的函数值数列即为插值结果。图 2为某一深度8扇区方位伽马数据 (红色点) 经插值处理后的曲线 (蓝色曲线)。图 2中0° (或360°) 和45°对应的伽马测量值分别代表图 1(b) 中标号为1和2的扇区值，依次类推。两扇区值之间按照一定的度数 (例如5°) 进行插值处理。

图 2

Fig. 2

下载eps/tif图 图 2 8扇区方位伽马数据插值处理曲线 Fig. 2 Interpolation processing curve of eight sectors azimuthal gamma data

为了反映出更加清晰的地层特征，通常需要将伽马测量数据映射为颜色矩阵，再按照颜色的深浅进行排列显示，即根据不同的地质工程需要设计特定色谱，以方便对地层特征进行观察和识别。

伽马图像的显示效果与色谱的选择密切相关。一般情况下选择浅色表示低伽马值，暗色表示高伽马值，这样生成的伽马图像既能与实际地层的自然特征相符合，又能与行业内通用的电阻率颜色关系相对应。本文伽马成像采用的色谱基色为白、橙、黄、褐、黑这5种颜色，采用的色谱级别数为64 (通常情况下色谱级别数≤ 64)，通过线性插值得到相邻两基色之间等级为64的色谱条。为了更加切合人的视觉特点，通常用色调 (Hue)、色度 (Saturation) 和亮度 (Intensity) 组成的HSI颜色空间来描述颜色。因此，需要利用线性插值完成对HSI颜色空间的插值运算。由于RGB颜色标准是目前计算机中运用最广的颜色系统，图像大多以RGB色彩模式存储，因此，为了实现HSI颜色空间内颜色的线性插值，需要在HSI颜色空间与RGB颜色空间之间进行转换。

表 1列出了几种常用的RGB与HSI颜色空间模型的转换方法^[13]。本文采用RGB-HSI对应关系更加准确的坐标变换法。坐标变换法是Castleman等^[14]基于RGB立方体，通过直角坐标系的旋转求出转换矩阵，并与极坐标系进行转换，最终得出转换公式，其颜色空间转换关系为

表 1(Table 1)

表 1 几种常用的RGB-HSI转换公式 Table 1 Several commonly used RGB-HSI conversion formulas 算法名称 色调 色度 亮度 几何推导法 $H=\left\{ \begin{align} & \theta ,G\ge B \\ & 2\text{ }\!\!\pi\!\!\text{ }-\theta ,G < B \\ \end{align} \right.$ $S=1-\frac{3\ \min \left( R, G, B \right)}{R+G+B}$ $I=\frac{R+G+B}{3}$ $\theta ={{\cos }^{-1}}\left[ \frac{\left( R-G \right)+\left( R-B \right)}{2\sqrt{{{\left( R-G \right)}^{2}}+\left( R-B \right)\left( G-B \right)}} \right]$ 坐标变换法 $\ H=\left\{ \begin{align} & \theta ,\ \ \ \ \ \ \ \ G\ge B \\ & \theta +\text{ }\!\!\pi\!\!\text{ },G < B \\ \end{align} \right.$ $S=\frac{2}{\sqrt{6}}\times \sqrt{{{\left( R-G \right)}^{2}}+\left( R-B \right)\left( G-B \right)}$ $I=\frac{R+G+B}{\sqrt{3}}$ $\theta =\frac{\text{ }\!\!\pi\!\!\text{ }}{2}-{{\tan }^{-1}}\left[ \frac{2R-G-B}{\sqrt{3}\left( G-B \right)} \right]$ 分段定义法 $H=\left\{ \begin{align} & \frac{\text{ }\!\!\pi\!\!\text{ }}{3}\times \frac{G-B}{Max-Min},Max=R \\ & \frac{\text{ }\!\!\pi\!\!\text{ }}{3}\times \frac{B-R}{Max-Min}+\frac{\text{2 }\!\!\pi\!\!\text{ }}{3},Max=G \\ & \frac{\text{ }\!\!\pi\!\!\text{ }}{3}\times \frac{R-G}{Max-Min}+\frac{\text{4 }\!\!\pi\!\!\text{ }}{3},Max=B \\ \end{align} \right.$ $S=\left\{ \begin{align} &\frac{Max-Min}{Max+Min}, 0 < I\le \frac{1}{2} \\ &\frac{Max-Min}{2-\left( Max+Min \right)}, I>\frac{1}{2} \\ \end{align} \right.$ $I=\frac{1}{2}\left( Max+Min \right)$ $H=H+\text{2 }\!\!\pi\!\!\text{ },H < 0$   注：Max=max(R，G，B)，Min=min(R，G，B)。公式中的R，G，B在计算前均归一化至[0,1]区间

下载CSV 表 1 几种常用的RGB-HSI转换公式 Table 1 Several commonly used RGB-HSI conversion formulas

通过HSI与RGB颜色空间的相互转换，得到256色的成像色谱条 (图 3)。

图 3

Fig. 3

下载eps/tif图 图 3 方位伽马图像色谱条 Fig. 3 Chromatography of azimuthal gamma images

静态色度标定是对整个绘图井段内的伽马测量数据从最小值到最大值进行颜色的映射，以保证整个井段内所生成的伽马图像颜色与测量值保持一致[图 4(a)]。静态色度标定适合于在较大范围内观察地层的测井响应和岩性对比，其优点是能够反映所钻遇地层放射性强弱的整体变化趋势，缺点是局部清晰度较差。静态色度标定步骤为：

图 4

Fig. 4

下载eps/tif图 图 4 静态与动态色度标定对比 Fig. 4 Comparison of static and dynamic color calibration

① 得到全井段所有扇区伽马测量数据的最大值V_max和最小值V_min；

② 将伽马最值V_min，V_max与色标的最值C_min，C_max一一对应，计算对应系数S，V_offset：

③ 将伽马数据映射为色标值，进而完成静态色度标定

式 (4)~ (6) 中：S代表刻度系数；V_offset代表V_min对应的色标值；V_pixel代表映射的色标值；V_i代表伽马测量值。

动态色度标定是在局部深度范围内进行的静态色度标定[图 4(b) ]，通常需要一个局部滑动窗长和一个移动步长。首先选取滑动窗长并在此窗长范围内进行静态色度标定，然后按照一定的步长向下 (或向上) 移动窗口，重复进行静态色度标定，直到标定完整个测量井段的伽马数据为止。一般情况下，为了保证伽马成像测井图像具有连续性，步长的选择通常小于窗长，使相邻的窗口之间产生部分重叠。

动态色度标定使随钻伽马图像失去了全井段图像的整体变化特征，但能够增加图像局部的特征清晰度，从而更好地识别一些细微的地质现象，如辨别孔洞、裂缝等构造^[15-16]。

选取H1井的随钻测井资料进行实例说明。该井开发的是厚油层顶部剩余油储量，目标层上、下均为致密泥岩盖层，油层薄且倾角的不确定性较大，而且设计要求A，B靶点垂深与油层顶界面的垂向距离不超过1 m，这就限制了B靶点在实际施工中只能有很小的垂深变化范围，因此相对增加了水平段井眼轨迹的控制难度。

为此，采用随钻多扇区方位伽马和电磁波电阻率仪器进行地质导向施工。通过方位伽马、伽马成像以及随钻电磁波电阻率的边界效应及时发现边界，确定进入储层的最佳时机，以便工程上及时调整，使轨迹快速返回目标层，显示了伽马成像仪器的优势。

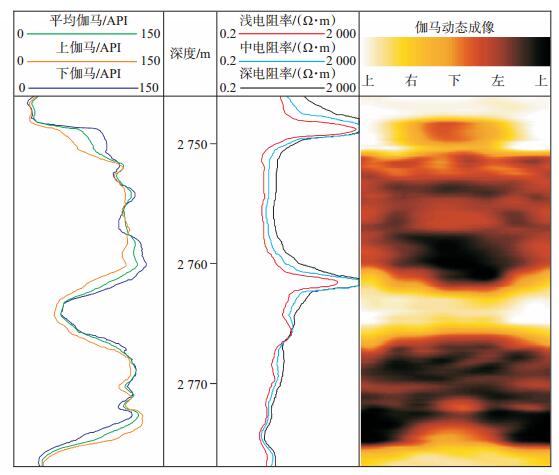
图 5是H1井随钻方位伽马、电磁波电阻率及伽马成像资料在不同地层中的应用实例。从图 5可以看出，在井深2 741 m处机械钻速开始降低，不同探测深度的电磁波电阻率曲线出现明显的分离 (探测深度大)，方位伽马曲线并未出现分离 (探测深度小)，说明距离仪器较近地层的电阻率为低值，距离仪器较远地层的电阻为高值，方位伽马只能探测到近处地层的放射性强度为高值，这一现象正是由于仪器贴近油层界面所造成的。暂停钻进后，根据循环上返的岩屑和气测值分析，也证明了这一判断的正确性。

图 5

Fig. 5

下载eps/tif图 图 5 随钻方位伽马成像测井资料 Fig. 5 Imaging logging data of LWD azimuthal gamma

由于测量仪器挂接在动力钻具之后，虽然此时仪器显示正在接近非储层界面但还未穿出油层，但由于仪器零长的原因，预计此时钻头很有可能已经接触油层底部，因此必须及时调整井眼轨迹才能避免钻头穿出油层。在井深2 748.6 m处，下伽马测量值逐渐大于上伽马测量值并出现明显分离，地层界面自然伽马成像明显，此后方位伽马值基本一致，且保持高值，电磁波电阻率保持低值，判断钻头深度在2 751 m附近穿出油层，在2 761 m后重新进入油层。由于井斜调整过大，导致钻头在2 772.5 m贴近储层顶部，此时应及时对井眼轨迹进行微调，确保钻头一直在目的层中穿行直到完钻。

现场应用表明，利用随钻方位伽马以及伽马成像仪器，可以确定进入储层的最佳时机，提高油层穿透率和对井眼轨迹的控制能力，进而更好地指导地质导向钻井施工。

(1) 在钻井过程中井下仪器测量数据传输速率不高的情况下，通过插值处理得到了360°全方位信息的伽马测井曲线，再通过RGB与HSI颜色空间的转换和色度标定，获得了全井壁伽马成像测井图像，实现了对地层特征的精细描述和识别。

(2) 利用随钻方位伽马数据成像化处理方法对现场实际资料进行处理，获得了效果较好的伽马成像测井图像，直观反映了井壁地层不同方位的岩性变化情况，确定进入储层的最佳时机，从而降低打穿油层的风险。

(3) 随钻成像测井是随钻测井技术的一个重要发展方向，基于伽马成像测井资料，可以进一步计算地层倾角、进行构造分析，将为复杂油气藏的勘探开发提供一种低成本、精细化的地质导向技术，从而指导钻井施工，特别是在目前低油价时期，在现场生产中具有广泛应用价值。