2. 美国能新科国际有限公司, 北京 100022;
3. 中国石化华北油田分公司 工程技术研究院, 郑州 450000
2. Energy New Technologies International Corporation, Beijing 100022, China;
3. Research Institute of Engineering and Technology, NorthChina Branch Company, Sinopec, Zhengzhou 450000, China
水平井技术及水力压裂技术已经广泛应用于油气田开发中[1-4],为油气资源的高效开发奠定了基础。在水平井分段改造工艺中应用最多的是可钻桥塞分段改造工艺[5-6],这主要是因为该工艺能够实现多簇分段改造,更有利于实现体积改造[7-8]。一般情况下,复合可钻桥塞采用电缆方式下入[9],为了施工安全,在压裂过程中往往需要进行过顶替作业,而过顶替作业会导致裂缝缝口的导流能力降低,从而降低压裂井的产能。目前已有的压裂水平气井的产能模拟模型都没有考虑过顶替对压裂后产能的影响,因此无法判断过顶替对压裂水平气井产能的影响程度。为此,根据过顶替后裂缝缝口和过顶替影响区域水力裂缝闭合后的特征及气体不稳定渗流理论,结合点源理论及势叠加原理[10-11],建立新的过顶替作业下压裂水平气井的产能模拟模型,以期为研究过顶替作业对压裂水平气井产能的影响提供方法,为水平井分段压裂设计优化提供指导。
1 过顶替影响区域相关计算模型及压裂水平气井产能模拟模型 1.1 过顶替影响区域的计算模型首先假设正常顶替结束时的动态裂缝宽度和高度在过顶替施工期间不再发生变化,即过顶替影响区域内动态裂缝的形状为长方体,且排量与正常顶替情况下的排量保持一致。考虑压裂液的可压缩性,根据体积守恒定律可得
| $ \Delta {{V}_{\text{d}i}}=\Delta {{L}_{\text{tf}i}}{{H}_{\text{tf}i}}{{W}_{\text{tf}i}}={{V}_{\text{gl}i}}-\Delta {{V}_{\text{q}}}-{{V}_{\text{ls}i}} $ | (1) |
式中:ΔVdi为过顶替影响区域内裂缝的总体积,m3;ΔLtfi为第i条裂缝过顶替影响区域内的裂缝长度,m;Htfi,Wtfi分别为第i条裂缝的动态裂缝高度和宽度,m;Vgli为第i条裂缝过量顶替液体积,m3;ΔVq为液体压缩量,m3;Vlsi为第i条裂缝过顶替部分滤失量,m3。
根据Harrington等通过大量裂缝滤失量实验研究提出的裂缝面总滤失量经验公式[12]可知,第i条裂缝过顶替部分的滤失量为
| $ {{V}_{\text{ls}i}}={{A}_{\text{gl}i}}\sqrt{60}{{C}_{\text{t}}}{{\left( \frac{8{{V}_{\text{gl}i}}}{{{Q}_{i}}} \right)}^{0.5}}=\Delta {{L}_{\text{tf}i}}{{H}_{\text{tf}i}}\sqrt{60}{{C}_{\text{t}}}{{\left( \frac{8{{V}_{\text{gl}i}}}{{{Q}_{i}}} \right)}^{0.5}} $ | (2) |
式中:Agli为第i条裂缝过顶替影响区域内的裂缝单壁面面积,m2;Ct为综合滤失系数,m/min0.5;Qi为过顶替施工排量,m3/min。
根据液体压缩系数的定义,可得压裂施工中过顶替部分液量的体积变化量为
| $ \Delta {{V}_{\text{q}}}={{V}_{\text{gl}i}}{{C}_{\text{y}}}\left( {{P}_{\text{d}}}-{{P}_{\text{s}}} \right) $ | (3) |
式中:Cy为压裂液压缩系数,MPa-1;Pd为过顶替期间井筒内平均压力,MPa;Ps为地面大气压力,MPa。
将式(2)和式(3)带入式(1),可得
| $ \Delta {{L}_{\text{tf}i}}{{H}_{\text{tf}i}}{{W}_{\text{tf}i}}={{V}_{\text{gl}i}}-{{V}_{\text{gl}i}}{{C}_{\text{y}}}\left( {{P}_{\text{d}}}-{{P}_{\text{s}}} \right)-{{L}_{\text{tf}i}}{{H}_{\text{tf}i}}\sqrt{60}{{C}_{\text{t}}}{{\left( \frac{8{{V}_{\text{gl}i}}}{{{Q}_{i}}} \right)}^{0.5}} $ | (4) |
对式(4)进行整理变换,可得到过顶替影响区域长度的计算公式为
| $ \Delta {{L}_{\text{tf}i}}=\frac{{{V}_{\text{gl}i}}\left[1-{{C}_{\text{y}}}\left( {{P}_{\text{d}}}-{{P}_{\text{S}}} \right) \right]}{{{H}_{\text{tf}i}}\left[{{W}_{\text{tf}i}}+\sqrt{60}{{C}_{\text{t}}}{{\left( \frac{8{{V}_{\text{gl}i}}}{{{Q}_{i}}} \right)}^{0.5}} \right]} $ | (5) |
假设在过顶替情况下,支撑剂全部被驱替到过顶替影响区域之外的裂缝内,即过顶替影响区域裂缝内无支撑剂,区域内裂缝仅靠壁面岩石颗粒支撑。假设裂缝壁面粗糙全部由岩石颗粒凸起所造成,且颗粒凸起为半球状,呈层状、菱形排列,原始条件下不变形且不破碎,同时,忽略返排时的支撑剂回流对过顶替影响区域内裂缝导流能力的影响。根据上述假设条件,可得到裂缝内总的球状颗粒数[13]为
| $ {{N}_{\text{t}}}=2\times \left[{{\left( \frac{{{H}_{\text{df}i}}-2R}{\frac{\sqrt{3}}{2}\times 2R}+1 \right)}_{\operatorname{int}}}-1 \right]\times {{\left( \frac{{{L}_{\text{df}i}}}{2R} \right)}_{\operatorname{int}}} $ | (6) |
式中:Nt为裂缝内总的球状颗粒数,个;Ldfi,Hdfi分别为第i条裂缝过顶替影响区域内裂缝的闭合长度和高度,m;R为球状颗粒半径,m。
裂缝凸起会在裂缝内形成孔隙,按照孔隙度的概念,引入水力裂缝孔隙度概念。根据体积守恒原理,则过顶替影响区域内的裂缝孔隙度为
| $ {{\varphi }_{\text{f}}}=\frac{{{L}_{\text{df}i}}{{H}_{\text{df}i}}{{W}_{\text{df}i}}-\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }{{N}_{\text{t}}}{{R}^{3}}}{{{L}_{\text{df}i}}{{H}_{\text{df}i}}{{W}_{\text{df}i}}} $ | (7) |
式中:φf为裂缝孔隙度,%;Wdfi为第i条裂缝过顶替影响区域内裂缝的闭合宽度,m。
其中,根据假设条件可知
根据Carman-Kozeny公式[14],渗透率与孔道大小的关系式为
| $ K=\frac{\varphi {{r}^{2}}}{8{{\tau }^{2}}} $ | (8) |
式中:K为地层渗透率,D;φ为地层孔隙度,%;r为孔隙半径,m;τ为迂回度。
将式(7)带入式(8)进行整理,并根据裂缝导流能力的定义可得
| $ {{F}_{\text{Cdf}i}}={{K}_{\text{df}i}}{{W}_{\text{df}i}}=\frac{\left( {{L}_{\text{df}i}}{{H}_{\text{df}i}}{{W}_{\text{df}i}}-\frac{2}{3}\text{ }\!\!\pi\!\!\text{ }{{N}_{\text{t}}}{{R}^{3}} \right){{r}^{2}}\times {{10}^{12}}}{8{{\tau }^{2}}{{L}_{\text{df}i}}{{H}_{\text{df}i}}} $ | (9) |
式中:FCdfi为第i条裂缝过顶替影响区域内裂缝的导流能力,D∙cm;Kdfi为第i条裂缝过顶替影响区域内裂缝的渗透率,D。
随着闭合应力的变化,裂缝的导流能力会发生变化。为了表征裂缝导流能力随闭合应力变化的关系,采用Walsh[15]关于裂缝粗糙表面作层流流动下的裂缝导流能力模型,则可得
| $ F{{'}_{\text{C}}}={{F}_{\text{C0}}}{{\left[1-\frac{\sqrt{2}\delta }{{{W}_{\sigma \text{0}}}}\ln \left( \frac{\sigma }{{{\sigma }_{0}}} \right) \right]}^{3}} $ | (10) |
式中:F′C,FC0分别为闭合应力和初始闭合应力下的导流能力,D∙cm;δ为裂缝面粗糙高度均方根,m;Wσ0为初始闭合应力下的裂缝宽度,m;σ,σ0分别为闭合应力和初始闭合应力,MPa。
1.3 基于不稳定渗流模型的压裂水平气井产能模拟模型在正常顶替情况下,可以根据不稳定渗流模型,将对称双翼裂缝进行等分离散,应用点源理论及势叠加原理推导出压裂水平气井的流动过程[10-11],即
| $ P_{i}^{2}\frac{A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)}{2}-P_{\text{wf}}^{2}=\frac{{{q}_{\text{f}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\left( \ln \frac{\sqrt{\frac{{{L}_{\text{f}i}}h}{\text{ }\!\!\pi\!\!\text{ }}}}{{{r}_{\text{w}}}}+S \right) $ | (11) |
其中
| $ \begin{align} &A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)=\sum\limits_{k=1}^{N}{\left\{ \sum\limits_{j=1}^{n}{\frac{{{q}_{\text{fl}kj}}\mu }{2\text{ }\!\!\pi\!\!\text{ }Kh}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}} \right.\left\{-Ei\left[-\frac{{{\left(-a{{x}_{\text{fl}i}}+b{{x}_{\text{fl}k}} \right)}^{2}}+{{\left( {{y}_{\text{f}i}}-{{y}_{\text{f}k}} \right)}^{2}}}{4\varphi t} \right] \right\}} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{\frac{{{q}_{\text{fr}kj}}\mu }{2\text{ }\!\!\pi\!\!\text{ }Kh}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}}\left. \left\{ -Ei\left[-\frac{{{\left(-a{{x}_{\text{fl}i}}-c{{x}_{\text{fr}k}} \right)}^{2}}+{{\left( {{y}_{\text{f}i}}-{{y}_{\text{f}k}} \right)}^{2}}}{4\varphi t} \right] \right\} \right\}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{k=1}^{N}{\left\{ \sum\limits_{j=1}^{n}{\frac{{{q}_{\text{fl}kj}}\mu }{2\text{ }\!\!\pi\!\!\text{ }Kh}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}} \right.\left\{ -Ei\left[-\frac{{{\left(-a{{x}_{\text{fr}i}}+b{{x}_{\text{fl}k}} \right)}^{2}}+{{\left( {{y}_{\text{f}i}}-{{y}_{\text{f}k}} \right)}^{2}}}{4\varphi t} \right] \right\}}+ \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \sum\limits_{j=1}^{n}{\frac{{{q}_{\text{fr}kj}}\mu }{2\text{ }\!\!\pi\!\!\text{ }Kh}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}}\left. \left\{ -Ei\left[-\frac{{{\left(-a{{x}_{\text{fr}i}}-c{{x}_{\text{fr}k}} \right)}^{2}}+{{\left( {{y}_{\text{f}i}}-{{y}_{\text{f}k}} \right)}^{2}}}{4\varphi t} \right] \right\} \right\} \\ &\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \left( a=1-\frac{1}{2n}, b=\frac{2n-2j+1}{2n}, c=\frac{2j-1}{2n} \right) \\ \end{align} $ |
式中:Pi,Pwf分别为边界压力和井底流压,MPa;qfi为第i条裂缝的产量,m3/s;μ为天然气黏度,10-6Pa·s;Z为偏差因子;T,Ts分别为地层温度和地面标准温度,K;FCfi为第i条裂缝支撑剂区域的导流能力,D∙cm;Lfi为第i条裂缝正常顶替情况下的裂缝长度,m;h为储层有效厚度,m;rw为井筒半径,m;S为表皮系数;qflkj,qfrkj第k条裂缝第j个微元的左、右翼产量,m3/s;xfli,xfri,xflk,xfrk分别为第i和第k条裂缝的左、右翼长度,m;yfi,yfk分别为第i条和第k条裂缝的纵坐标,m;φ为导压系数;t为渗透时间,s;-Ei(-x) 为幂积分函数。
在式(11)中将裂缝面等效成圆饼状泄流形状,这与实际的情况有一定出入。因为一般情况下裂缝长度都远大于储层厚度,因此,把裂缝面看成矩形泄流更符合实际情况。根据采油工程知识[16],引入等效系数Cx,则式(11)可变为
| $ P_{i}^{2}-\frac{A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)}{2}-P_{\text{wf}}^{2}=\frac{{{q}_{\text{f}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\left( \ln \frac{{{C}_{x}}\sqrt{{{L}_{\text{f}i}}h}}{{{r}_{\text{w}}}}+S \right) $ | (12) |
式中:Cx为等效系数。
由于裂缝是气体流动的主要通道,流动压降也主要发生在裂缝内,类似于表皮系数,因此,考虑高速非达西渗流的水平气井流动表达式为
| $ \begin{align} &P_{i}^{2}-\frac{A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)}{2}-P_{\text{wf}}^{2}= \\ &\ \ \ \ \ \ \ \ \ \frac{{{q}_{\text{f}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\left( \ln \frac{{{C}_{x}}\sqrt{{{L}_{\text{f}i}}h}}{{{r}_{\text{w}}}}+S+D{{q}_{\text{f}i}} \right) \\ \end{align} $ | (13) |
式中:Dqfi为流量相关表皮系数。
结合Cooke [17]关于不同粒径下速度系数的表达式,则式(13)中的D可表示为
| $ D=2.191\times {{10}^{-18}}\frac{7.021\times {{10}^{12}}}{K_{\text{f}i}^{0.6}{{r}_{\text{g}}}\cdot \mu {{W}_{\text{f}i}}{{r}_{\text{w}}}} $ | (14) |
式中:Kfi为第i条裂缝正常顶替下的裂缝渗透率,μm2;Wfi为第i条裂缝正常顶替下的裂缝宽度,m;rg为气体相对密度。
2 过顶替情况下压裂水平气井的产能模拟模型由于过顶替会造成裂缝缝口的导流能力下降,因此式(13)也不能直接用于表述过顶替情况的流动,需要进行深入研究。为了处理方便,对裂缝过顶替影响区域、水力支撑裂缝区域及井筒作如下假设:①将支撑裂缝远端至过顶替影响区域外边界看成一个渗流单元,将过顶替影响区域外边界至井筒看成另外一个渗流单元,2个渗流单元均按照径向流处理;②由于支撑裂缝的导流能力远大于过顶替影响区域裂缝的导流能力,因此仅考虑过顶替影响区域裂缝的压降和表皮效应;③由于一般情况下过顶替液量比较小,因此,支撑裂缝长度远大于过顶替影响区域范围,所以只研究支撑裂缝间的裂缝干扰,即忽略过顶替影响区域内的裂缝与其他裂缝间的相互影响;④忽略过顶替对正常顶替情况下形成的支撑裂缝参数的影响,只考虑支撑裂缝起始位置变化;⑤忽略井筒流动压降。
根据假设条件①和②,按照式(11)水平气井流动表达式,可得出渗流外边界到过顶替影响区域外边界的压裂水平气井流动表达式,即
| $ P_{i}^{2}-\frac{A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)}{2}-P_{\text{df}i}^{2}=\frac{{{q}_{\text{f}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\ln \frac{{{C}_{xi}}\sqrt{{{L}_{\text{f}i}}h}}{{{C}_{\text{d}xi}}\sqrt{{{L}_{\text{df}i}}h}} $ | (15) |
式中:Pdfi为第i条裂缝过顶替影响区域外边界压力,MPa;Cdxi,Cxi分别为第i条裂缝过顶替影响区域和支撑裂缝区域的等效系数。
同理,根据假设条件③,可以得到过顶替影响区域外边界到井筒的压裂水平气井流动表达式,即
| $ P_{\text{df}i}^{2}-P_{\text{wf}}^{2}=\frac{{{q}_{\text{df}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cdf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\left( \ln \frac{{{C}_{\text{d}xi}}\sqrt{{{L}_{\text{df}i}}h}}{{{r}_{\text{w}}}}+S \right) $ | (16) |
式中:qdfi为第i条裂缝过顶替影响区域的产量,m3/s。
由于裂缝缝口导流能力降低会在裂缝内形成高速非达西效应,为了表述高速非达西渗流对压裂水平气井产能的影响,将式(16)作类似于式(13)的处理,可得
| $ P_{\text{df}i}^{2}-P_{\text{wf}}^{2}=\frac{{{q}_{\text{df}i}}\mu }{\text{ }\!\!\pi\!\!\text{ }{{F}_{\text{Cdf}i}}}\frac{ZT{{P}_{\text{s}}}}{{{T}_{\text{s}}}}\left( \ln \frac{{{C}_{\text{d}xi}}\sqrt{{{L}_{\text{df}i}}h}}{{{r}_{\text{w}}}}+S+{{D}_{\text{df}i}}{{q}_{\text{df}i}} \right) $ | (17) |
式中:Ddfiqdfi为过顶替影响区域流量的相关表皮系数。
对于同一条裂缝,有qfi = qdfi,联立式(15)和式(17),通过变形和整理可得到过顶替作业影响下的压裂水平气井流动表达式,即
| $ P_{i}^{2}-\frac{A\left( {{x}_{\text{f}i}}, {{y}_{\text{f}i}}, t \right)}{2}-P_{\text{wf}}^{2}={{q}_{\text{f}i}}\frac{\mu ZT{{P}_{\text{s}}}}{\text{ }\!\!\pi\!\!\text{ }{{T}_{\text{s}}}}\left[\frac{1}{{{F}_{\text{Cf}i}}}\ln \frac{{{C}_{xi}}\sqrt{{{L}_{\text{f}i}}}}{{{C}_{\text{d}xi}}\sqrt{{{L}_{\text{df}i}}}}+\frac{1}{{{F}_{\text{Cdf}i}}}\left( \ln \frac{{{C}_{\text{d}xi}}\sqrt{{{L}_{\text{df}i}}h}}{{{r}_{\text{w}}}}+S+{{D}_{\text{df}i}}{{q}_{\text{df}i}} \right) \right] $ | (18) |
某压裂水平气井的参数如下:储层厚度为12 m,储层渗透率为5 mD,储层颗粒直径分别取0.10 mm,0.15 mm,0.20 mm;水平段长度为500 m,分5段进行改造,裂缝间距为100 m,支撑裂缝长度为300 m,支撑裂缝平均导流能力为20 D·cm,正常顶替结束时动态裂缝宽度为0.8 cm,动态裂缝高度为35 m,施工排量为4 m3/min,过顶替压裂施工平均井筒压力为40 MPa;气体黏度为0.022 mPa·s,偏差因子为0.957,井筒半径为0.1 m,原始地层压力为28.2 MPa,井底流压为23.6 MPa,地层温度为90 ℃。计算结果如表 1所列。
|
|
下载CSV 表 1 压裂水平气井模拟计算结果 Table 1 Production simulation of fractured horizontal gas wells |
为了更清晰地研究过顶替对压裂水平气井产能的影响,特别是过顶替影响区域裂缝的导流能力、过顶替液量大小、储层颗粒粒径以及高速非达西渗流对压裂水平气井产能的影响,利用所建立的模型对上述主要影响因素进行了实例计算和简要分析。
3.1 过顶替对压裂水平气井产能的影响从图 1可以看出,在仅考虑壁面粗糙度支撑裂缝的情况下,过顶替作业对压裂水平气井的产能影响很大。在过顶替8 m3的情况下,过顶替影响区域长度为8.16 m,在生产300 d时压裂水平气井的产量仅为正常顶替情况下的11.34%,为正常顶替并考虑非达西渗流时的12.69%。这主要是由于本文所建立的模型假设了过量顶替液将裂缝缝口的支撑剂全部驱替至过顶替影响区域外的裂缝内,过顶替影响区域仅靠裂缝表面的粗糙度支撑,从而导致裂缝缝口的导流能力下降很多,相当于在井筒附近形成了较大的流动阻力,从而降低了压裂水平气井的产能。
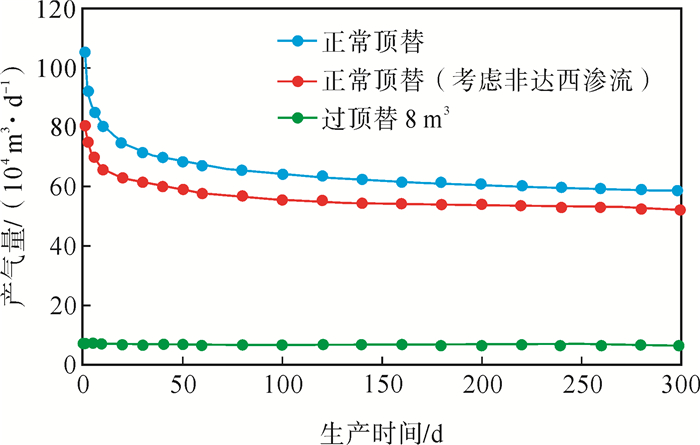
|
下载eps/tif图 图 1 过顶替对压裂水平气井产能的影响 Fig. 1 The effect of overdisplacing operation on production performance of fractured horizontal gas wells |
从图 2可以看出,不同过顶替影响区域内裂缝的导流能力对压裂水平气井的产能影响明显。过顶替影响区域的裂缝导流能力越低,则产量下降越大。在实际情况中,由于支撑剂的沉降作用会在顶替完成之前就在裂缝缝口形成砂堆,且顶替液往往采用黏度较低的液体,因此,即使过顶替也不会完全将支撑剂从缝口推进到裂缝深处。即便如此,过顶替也会让缝口的导流能力受到影响,对产能的影响也会因缝口导流能力的降低而增加。
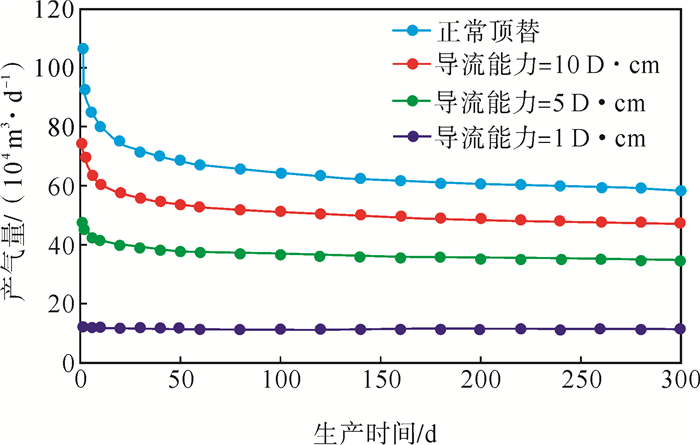
|
下载eps/tif图 图 2 不同过顶替影响区域裂缝导流能力对压裂水平气井产能的影响 Fig. 2 The effect of different fracture conductivity of the overdisplacing sweep region on production performance of fractured horizontal gas wells |
利用过顶替影响区域计算模型,得到在不同过顶替液量情况下其影响范围的计算结果(表 2)。从表 2可以看出,随着过顶替液量的增加,过顶替影响区域不断增大,但增大幅度在降低。从图 3可以看出,过顶替液量越多,压裂水平气井的产量降低就越大,但随着过顶替液量的增加,产能的降低程度在减小。这是因为过顶替影响区域的裂缝导流能力不随过顶替影响区域的变化而变化,当过顶替影响区域的裂缝形成时,就会在近井地带形成明显的流动阻力,这种阻力不会随影响区域的增大而剧烈增加,因此,随着过顶替液量的增加,其对产能的影响程度在下降。
|
|
下载CSV 表 2 不同过顶替液量的影响范围 Table 2 Effect region of different overdisplacing liquid volum |
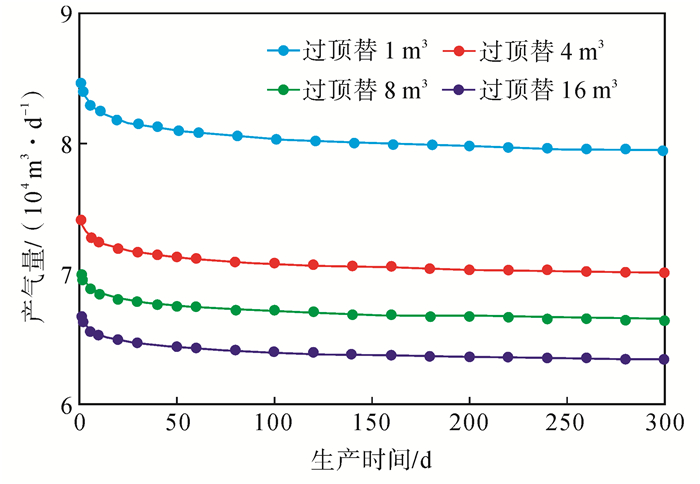
|
下载eps/tif图 图 3 不同过顶替量对压裂水平气井产能的影响 Fig. 3 The effect of different overdisplacing liquid volume on production performance of fractured horizontal gas wells |
从图 4可以看出,颗粒粒径越大,压裂水平气井的产量就越高。这是因为颗粒粒径的增大会使过顶替影响区域内的裂缝更类似于铺置双层支撑剂并在裂缝壁面嵌入一半的状态,随着颗粒粒径的增大,裂缝导流能力会增强,压裂水平气井的产能也会增加。
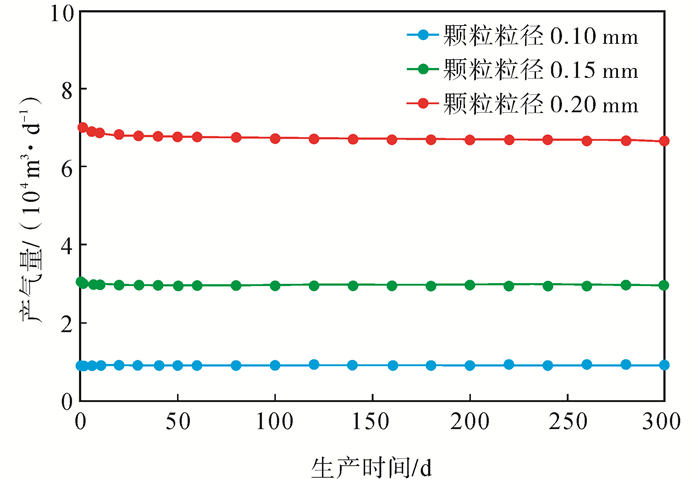
|
下载eps/tif图 图 4 不同岩石颗粒粒径对压裂水平气井产能的影响(过顶替8 m3) Fig. 4 The effect of different rock grain sizes on production performance of fractured horizontal gas wells |
从图 5可以看出,过顶替影响区域内的高速非达西渗流对压裂水平气井的产能影响较小。这是因为过顶替影响区域裂缝的导流能力比支撑裂缝的导流能力低很多,流动阻力使得压裂水平气井的产量降低,紊流效应减弱,致使高速非达西渗流的影响降低。
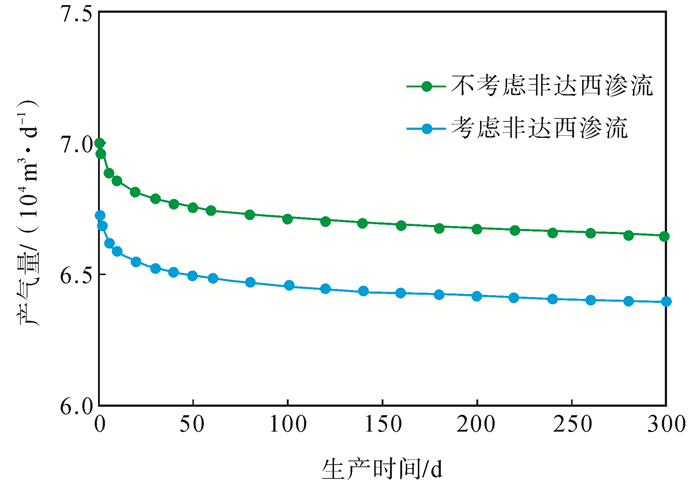
|
下载eps/tif图 图 5 过顶替区域高速非达西对压裂水平气井产能的影响(过顶替8 m3) Fig. 5 The effect of high velocity Non-Darcy flow on production performance of fractured horizontal gas wells in the overdisplacing sweep region |
(1)基于建立的过顶替影响区域计算模型、裂缝导流能力计算模型及不稳定渗流下的压裂水平气井产能模拟模型,建立了过顶替作业下压裂水平气井产能模拟模型。尽管在模型中对过顶替影响区域进行了简单处理,但建立的模型仍然能够定量表征过顶替对压裂水平气井产能的影响程度,较以往的模型更能反映出压裂水平气井的实际情况。
(2)在过顶替影响区域裂缝导流能力的计算模型中没有考虑支撑剂沉降形成的砂堆和支撑剂回流,而仅考虑了裂缝壁面的粗糙度,虽然与实际情况存在一定出入,但仍具有现实意义,即在水力压裂过程中采用低密度特别是超低密度支撑剂施工的井要尽可能避免过顶替作业。
(3)裂缝缝口的导流能力对压裂水平气井的产能起着至关重要的作用,提高裂缝缝口的导流能力对压裂效果的提高具有重要的意义,而过顶替作业会影响裂缝缝口的导流能力,因此,在压裂施工中应尽可能避免过顶替作业。
(4)过顶替影响区域的确定和裂缝导流能力的计算比较复杂,还需要进一步深入研究,以便能够建立更全面的模型来研究过顶替对压裂水平气井压后产能的影响,以指导压裂优化设计和施工。
| [1] |
吴奇, 胥云, 张守良, 等.
非常规油气藏体积改造技术核心理论与优化设计关键. 石油学报, 2014, 35(4): 706–714.
WU Q, XU Y, ZHANG S L, et al. 2014. The core theories and key optimization designs of volume stimulation technology for unconventional reservoirs. Acta Petrolei Sinica (in Chinese), 2014, 35(4): 706-714. DOI:10.7623/syxb201404011 |
| [2] |
张小龙, 张同伟, 李艳芳, 等.
页岩气勘探和开发进展综述. 岩性油气藏, 2013, 25(2): 116–122.
ZHANG X L, ZHANG T W, LI Y F, et al. 2013. Research advance in exploitation and development of shale gas. Lithologic Reservoirs (in Chinese), 2013, 25(2): 116-122. |
| [3] |
严向阳, 胡永全, 李楠, 等.
泥页岩地层破裂压力计算模型研究. 岩性油气藏, 2015, 27(2): 109–114.
YAN X Y, HU Y Q, LI N, et al. 2015. Calculation model of breakdown pressure in shale formation. Lithologic Reservoirs (in Chinese), 2015, 27(2): 109-114. |
| [4] |
王大为, 李晓平.
页岩气勘探和开发进展综述. 岩性油气藏, 2011, 23(2): 118–123.
WANG D W, LI X P. 2011. Advances in deliverability analysis of horizontal well. Lithologic Reservoirs (in Chinese), 2011, 23(2): 118-123. |
| [5] |
叶登胜, 李斌, 周正, 等.
新型速钻复合桥塞的开发与应用. 天然气工业, 2014, 34(4): 62–66.
YE D S, LI B, ZHOU Z, et al. 2014. Development and application of a new fast-drilling composite plug. Natural Gas Industry (in Chinese), 2014, 34(4): 62-66. |
| [6] |
任勇, 叶登胜, 李剑秋, 等.
易钻桥塞射孔联作技术在水平井分段压裂中的实践. 石油钻采工艺, 2013, 35(2): 90–93.
REN Y, YE D S, LI J Q, et al. 2013. Application of drillable bridge plug and clustering perforation in staged fracturing for horizontal well. Oil Drilling & Production Technology (in Chinese), 2013, 35(2): 90-93. |
| [7] |
赵金洲, 陈曦宇, 刘长宇, 等.
水平井分段多簇压裂缝间干扰影响分析. 天然气地球科学, 2015, 26(3): 533–538.
ZHAO J Z, CHEN X Y, LIU C Y, et al. 2015. The analysis of crack interaction in multi-stage horizontal fracturing. Natural Gas Geoscience (in Chinese), 2015, 26(3): 533-538. |
| [8] |
吴奇, 胥云, 王晓泉, 等.
非常规油气藏体积改造技术—内涵、优化设计与实现. 石油勘探与开发, 2012, 39(3): 352–358.
WU Q, XU Y, WANG X Q, et al. 2012. Volume fracturing technology of unconventional reservoirs: Connotation, optimization design and implementation. Petroleum Exploration & Development (in Chinese), 2012, 39(3): 352-358. |
| [9] |
严向阳, 王腾飞, 徐永辉, 等.
连续管坐塞与分簇射孔联作技术. 石油机械, 2015, 43(5): 107–110.
YAN X Y, WANG T F, XU Y H, et al. 2015. Joint operation of coil tubing plugging and cluster perforation. China Petroleum Machinery (in Chinese), 2015, 43(5): 107-110. |
| [10] |
徐严波, 齐桃, 杨凤波, 等.
压裂后水平井产能预测新模型. 石油学报, 2006, 27(1): 89–91.
XU Y B, QI T, YANG F B, et al. 2006. New model for productivity test of horizontal well after hydraulic fracturing. Acta Petrolei Sinica (in Chinese), 2006, 27(1): 89-91. DOI:10.7623/syxb200601019 |
| [11] |
胡永全, 严向阳, 赵金洲.
多段压裂水平气井紊流产能模拟模型—以塔里木盆地克拉苏气田大北区块为例. 天然气工业, 2013, 33(1): 1–4.
HU Y Q, YAN X Y, ZHAO J Z. 2013. A simulation model for the turbulent production of a multi-stage fractured gas well:a case study from the Dabei block in the Kelasu Gas Field, Tarim Basin. Natural Gas Industry (in Chinese), 2013, 33(1): 1-4. DOI:10.3787/j.issn.1000-0976.2013.01.001 |
| [12] |
蒋海, 杨兆中, 李小刚, 等.
裂缝面滤失对压裂井产能的影响分析. 长江大学学报 (自然科学版), 2008, 5(1): 87–89.
JIANG H, YANG Z Z, LI X G, et al. 2008. Analyses on the effect fracture surface leak-off on fractured well productivity. Journal of Yangtze University (Natural Science Edition) (in Chinese), 2008, 5(1): 87-89. |
| [13] |
吴国涛, 胥云, 杨振周, 等.
考虑支撑剂及其嵌入程度对支撑裂缝导流能力影响的数值模拟. 天然气工业, 2013, 31(5): 65–68.
WU G T, XU Y, YANG Z Z, et al. 2013. Numerical simulation considering the impact of proppant and its embedment degree on fracture flow conductivity. Natural Gas Industry (in Chinese), 2013, 31(5): 65-68. |
| [14] |
何更生.
油层物理. 北京: 石油工业出版社, 1994.
HE G S. Rreservoir physics (in Chinese) . Beijing: Ptroleum Industry Press, 1994. |
| [15] | WALSH J B. 1981. Effect of pore pressure and confining pressure on fracture permeability. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1981, 18(5): 429-435. |
| [16] |
李颖川.
采油工程. 北京: 石油工业出版社, 2002.
LI Y C. Oil production engineering (in Chinese) . Beijing: Ptroleum Industry Press, 2002. |
| [17] | COOKE C E. 1973. Conductivity of fractureproppants in multiple layers. SPE 4117, 1973. |
 2017, Vol. 29
2017, Vol. 29



