2. 西南石油大学 地球科学与技术学院, 成都 610500;
3. 中国石化胜利油田分公司 勘探开发研究院, 山东 东营 257015;
4. 重庆科技学院 复杂油气田勘探开发重庆市重点实验室, 重庆 401331
2. School of Geoscience and Technology, Southwest Petroleum University, Chengdu 610500, China;
3. Research Institute of Exploration and Development, Shengli Oilfield Company, Sinopec, Dongying 257015, Shandong, China;
4. Chongqing Key Laboratory of Complex Oil & Gas Field Exploration and Development, Chongqing University of Science & Technology, Chongqing 401331, China
旋回地层学(Cyclostratigraphy)作为地质学领域的分支学科一直是地层学、沉积学、层序地层学关注的热点。自旋回地层学概念提出以后,国内外许多学者对其进行了大量的研究[1-2],但“旋回”一词被广泛应用于地质学的各分支学科中,因而产生了一些混淆,尤其是和层序地层学中的旋回不能很好地区分。在这种背景下,国内从事天文地质学研究的学者徐道一等[3],为了突出地球轨道参数对沉积物规律性变化的影响,将研究这种影响因素的旋回地层学称为天文地层学。在此基础之上,姚益民等[4]以牛38井自然伽马曲线(GR)为依据,结合沉积、古生物、磁性等基础资料,对东营凹陷沙三段的天文地层旋回进行了划分;徐道一等[5]对新疆吐鲁番盆地下侏罗统、华北地区石炭系与二叠系、四川盆地上三叠统开展了天文旋回研究,通过提取测井资料中的地层信息,对地层进行了高分辨率旋回划分和对比;陈中红等[6]对东营凹陷牛38井古近系沙河街组三段的自然伽马和自然伽马能谱测井(NGS)曲线研究表明,在较稳定的还原性古环境中,能谱测井中的铀(U)含量和钍(Th)/铀比均是天文地层旋回的重要指示参数;Rampino等[7]对奥地利阿尔卑斯山Werfen组韵律性互层的浅海亚相白云质灰岩和泥页岩的自然伽马和密度数据进行旋回地层学研究,获得印度阶的Griesbachian亚阶的持续时间为1.4~1.6 Ma;Berger等[8]对瑞士Breggia Gorge地区下侏罗统3条灰岩与页岩剖面的层序进行功率谱分析,发现它们均存在21 ka的岁差周期。如上所述,许多研究均证实了地层中米兰科维奇旋回的存在,这便打破了传统生物地层及放射性地层划分的界限,为地层的划分与对比提供了新思路,并且提高了地层划分与对比的精度。另外,通过天文调谐(Astronomical tuning)可将气候替代性指标标定到地球轨道三要素上,可精确估算重大地质事件的持续时间[9]。因此,对天文地层学的研究有助于认识产生地层沉积旋回的根本驱动力,对复杂岩性地层的精细年代地层划分、地质分层均具有指导意义,对油气勘探与开发也具有一定的应用价值。笔者在调研国内外大量相关研究文献的基础上,总结天文地层学的含义、发展过程,分析旋回地层学和天文地层学的关系以及天文地层学的研究方法,并探讨天文地层学的发展方向。当前,随着非常规泥页岩油气勘探与开发的深入,对泥页岩细粒沉积地层的年代地层划分、地质分层精度要求越来越高,对米兰科维奇旋回的研究将进一步向精度更高的亚米兰科维奇旋回发展,利用连续的、高分辨率的测井曲线,同时结合同位素测年资料建立厚层泥页岩天文地层旋回及精细地层划分方法将是天文地层学今后研究的新方向。
1 旋回及旋回地层学 1.1 旋回及旋回地层旋回性是物质运动的基本特性,“旋回”一词在地质学的各个领域被广泛应用,它可以指一切回归起始点的系列事件。在沉积学和地层学中,旋回是表示具有重现性或周期性沉积记录的术语,能够指示沉积过程的时间周期性,具有描述性和解释性的双重含义[10]。对于旋回的研究也有不同的定义标准,Vail等[11]所提出的经典层序地层学将海平面的一次升降定义为一个旋回,Cross[12]的高分辨率层序地层学则将基准面的一次上升与下降定义为一个基准面旋回,而传统旋回地层学所说的旋回是指与地球轨道的周期性变化有关的地层重复,是由周期为10 ka至2 Ma的轨道变化控制形成的旋回。
旋回地层是指与沉积系统周期性变化有关的沉积记录和岩性变化的重复出现,是在地球轨道参数(天文参数)变化驱动下形成的,因地球轨道变化具有一定周期性,故旋回地层还具有一定的时间意义[9],而保存在地层中的旋回性沉积记录是天文周期控制或驱动沉积节律的最好历史见证。地层记录具有四大特性:复杂性、非渐变性、不完整性和旋回性[13],其中旋回性地层记录就是指不同级别的旋回层序及其有序叠加形式,是研究和识别沉积物以及沉积作用的空间变化与相对时间变化序列的重要依据。
1.2 旋回地层学研究进展旋回地层学是以米兰科维奇理论为基础的一门新兴的地层学分支学科。据文献[14]报道,1941年,南斯拉夫气候学家米兰科维奇为研究第四纪冰期成因提出了地球轨道三要素[偏心率(e)、黄赤交角(ε)和岁差(p)]周期性变化对冰期、间冰期的影响假说,并对地球轨道参数进行了定量计算,这一理论在当时并没有引起地学界的重视。直到1976年,Hays等[15]通过对南印度洋钻孔中有孔虫氧同位素的研究,发现了与偏心率、黄赤交角、岁差相当的旋回周期,验证了米兰科维奇旋回的存在,才引起了地质学家们对这一理论的广泛关注,从此开始了以米兰科维奇旋回理论为基础的旋回地层学研究工作[9]。
据文献[16]报道,“旋回地层学”一词是由Fischer等1988年在意大利Perugia召开的专业学术会议上首次提出,它是指研究受地球轨道周期性变化控制形成的地层序列的地层学分支学科,米兰科维奇旋回序列是旋回地层学研究的重点。2004年,Hilgen等[17]正式将旋回地层学定义为对地层记录的周期性旋回变化进行识别、描述、对比和成因解释,并将其应用于地质年代学中,以提高年代地层框架的精度和分辨率,从而实现地层高精度划分与对比的一门地层学分支学科。
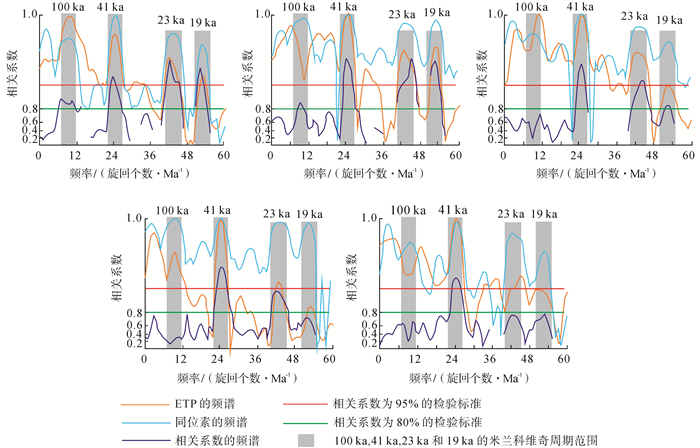
自旋回地层学这一概念提出以来,很多学者对其进行了广泛而深入的研究。田军等[18]以δ18O为调谐材料,将其与目标曲线(ETP曲线)进行交叉频谱分析(图 1),发现底栖有孔虫δ18O含量与地球轨道三要素密切相关,并在此基础上建立了新近纪以来中国南海海洋沉积的天文年代标尺,探讨了地球轨道参数对南海东亚季风演化及上层海水结构变化的驱动机制。龚一鸣等[16]对桂西南和桂东北碳酸盐岩台地—斜坡—盆地相区4条剖面进行研究,通过岩性识别旋回,得出超层束组与层束组之间的数量关系为1:3,层束组与层束之间的数量关系为1:6,与Berger等[8]对地球轨道进行天文计算得出的泥盆纪偏心率与斜度周期比值为1.0:3.1,偏心率与岁差周期比值为1.0:5.9相吻合。Zachos等[19]在研究渐新世—中新世海相地层时,在距今26~ 20 Ma的地层中识别出十几个约400 ka的偏心率周期。这些研究不仅进一步证明了米兰科维奇旋回的驱动作用,也为高分辨率地层划分和天文地质年代表的提出提供了依据。
|
下载eps/tif图 图 1 南海南部ODP1143站底栖有孔虫δ18O与地球轨道参数ETP的交叉频谱分析[24] Fig. 1 Cross spectrum analysis of ETP with δ18 O of benthic foraminifera at ODP1143 station in southern South China Sea |
旋回地层学是对传统地层学理论的补充,对油气勘探与开发发挥了重要作用,但在众多学者的应用过程中与地质学(层序地层学等)中的“旋回”概念产生了混淆及误解,为了突出地球轨道参数变化对地层沉积作用的影响,徐道一等[3]提出了“天文地层学”这一概念。天文地层学的提出强调了由地球引力场的周期性摄动引发的沉积旋回或古气候代替性指标的旋回[9],将地层旋回性的最终驱动力归结为地球轨道参数的周期性变化。
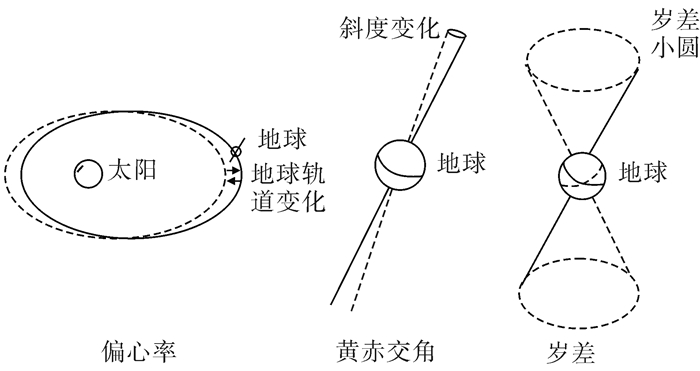
天文地层学主要研究内容之一是地球3个轨道要素:偏心率、黄赤交角和岁差的旋回(图 2)。偏心率的变化对地球公转的椭圆轨道产生影响,其循环形式造成了日地距离微小的季节性变化。天文理论计算表明,在距今10 Ma年以来,偏心率的主要周期为404 ka,95 ka,124 ka,99 ka,131 ka,2 360 ka和1 000 ka;黄赤交角是指地轴的倾斜度,它是地球公转的轨道面与地球赤道面的夹角,黄赤交角主要周期为41.0 ka,39.6 ka和53.6 ka;岁差是指在固体潮汐作用下导致“地球差异旋转”,从而导致回归年与恒星年产生时间差的天文现象,它能够反映偏心率和黄赤交角的综合影响,主要周期为23.7 ka,22.4 ka和19.0 ka[5, 20]。在距今500 Ma中,黄赤交角和岁差的周期值都在不断的变化,而偏心率周期值,尤其是振幅最大的404 ka周期值,在金星和木星万有引力的影响下,在地质历史时期非常稳定,变化较少。上述地球轨道的周期性变化势必引起气候的变化,并被记录在沉积地层当中,通常表现为沉积结构、构造、岩性与岩相等方面的变化[21]。这种变化由于是受天文力驱动的,在全球范围内具有可对比性。
|
下载eps/tif图 图 2 地球的轨道变化[23] Fig. 2 Orbit variation of earth |
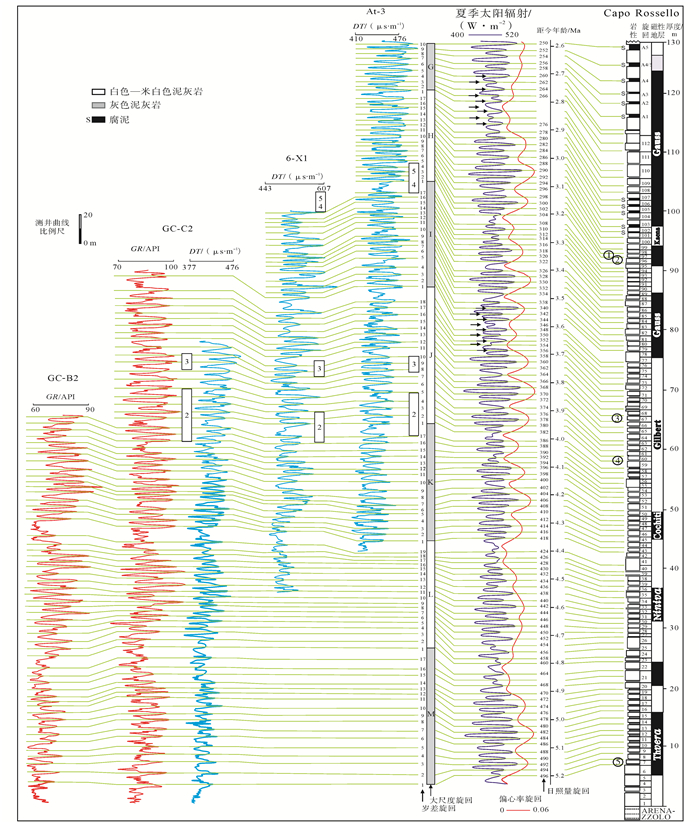
随着天文地层学这一概念的提出,国内一些学者将研究的重点转向产生地层旋回的地球轨道参数上来。在地层的记录中,经常可以见到3~5个(米级)旋回以数量比为1:4的叠置样式构成更大级别的旋回地层,或以4~6个旋回构成数量比为1:5的叠加。前者可能是400 ka的长偏心率旋回与100 ka的短偏心率旋回作用的产物,后者可能是短偏心率旋回和20 ka的岁差旋回作用的结果[13]。从天文地质学的角度出发,利用地层记录中的米兰科维奇周期特征,不同的学者对不同区域、不同时代的地层开展了大量的天文地层学研究,取得了许多研究进展,如Sierro等[23]研究西班牙南部加的斯湾(Gulf of Cadiz)上新世早期钻孔资料识别出与长偏心率周期相对应的优势周期,并在每一阶中找到与短偏心率对应的100 ka周期(图 3);龚一鸣等[24]对广西上泥盆统弗拉阶至法门阶12个牙形石带进行了天文年代定年,确定了生物存在年代及灭绝事件的持续年代;姚益民等[25]对新疆吐哈盆地侏罗系进行研究,利用测井资料发现长偏心率旋回周期为400 ka,并与北美上三叠统的优势旋回值相比较,两地区与米兰科维奇旋回相关的优势旋回值大都可以对比;徐道一等[5]通过对我国大陆30余口井的测井资料进行研究,总结了陆相地层的天文地层学研究方法,介绍了天文周期的理论值、测井资料的处理方法及地层单位年龄确定和延续时间的计算方法。其他学者也以地球轨道参数周期性变化导致的沉积旋回为研究对象,利用测井、氧同位素等古气候替代性指标,对天文地层周期开展了一系列研究。
|
下载eps/tif图 图 3 利用GR和DT曲线划分旋回结果与依据环地中海日照曲线小层划分及Capo Rossello剖面的碳酸盐旋回和磁性地层划分结果的对比[23] Fig. 3 Astronomical tuning of gammaray and sonic cyclicity, and summer insolation curve of astronomical solution in circum-Mediterranean, bed-to-bed correlation with Capo Rossello carbonate cycles and magnetostratigraphy ①Globoquadrina altispira最后一次出现;②Sphaeroidinellopsis seminulina最后一次出现;③Globorotalia margaritae最后一次大量出现;④G. margaritae最后一次出现;⑤S. seminulina顶峰时期 |
目前,我国学者对天文地层学的研究主要集中在东部的新生代地层[4]和南海中新世—更新世地层[23]。对于中生代及更古老的地层,由于经历了较长的地史时期,对天文年代校准还有一定的难度[20]。对于其他地区,如新疆吐哈盆地早侏罗世—中侏罗世[25]、桂西南和桂东北地区上泥盆统弗拉阶—法门阶盆地相和斜坡相碳酸盐岩[24]、珠江口盆地中新世—上新世[26]等地层虽有一定的研究,但均不如对东部渤海湾盆地的研究程度深,而对于四川盆地及周边地区的天文地层学研究开展得更少。对于新生代地层,测井曲线进行滤波处理后可以与Laskar等[27]理论的目标曲线对比,通过天文调谐可实现天文地质年代标尺的建立[20]。然而,对于中生代及更古老的地层需要通过运用其他方法进行综合研究,对地层年代进行精确标定,建立地层的绝对年代格架,减少直接使用天文调谐进行研究的盲目性,增强其精度与科学性[20]。目前,进行绝对年代标定的方法主要包括生物地层年代划分、磁性地层年代划分、同位素测年、ESR测年等[28],而通过高分辨率测井资料,结合放射性同位素、ESR测年及地球化学特征等方法,开展综合而深入的天文地层旋回识别及精细地层划分,这是今后天文地层学值得关注的方向。
2.3 天文地层学与旋回地层学的关系前文已述及,旋回地层学的提出最初是特指以轨道参数周期性变化而产生的旋回地层为研究对象的地层学分支学科,其更具体的表述应为轨道旋回地层学,而“天文地层学”这一概念的提出是为了避免与后期“旋回地层学”一词在广义的概念上容易与其他地层学分支当中的“旋回”(尤其是层序地层学中的旋回)相混淆。天文地层学与层序地层学所关注的旋回虽然都是以地层旋回作为研究对象,但其形成机制和研究方法不完全相同,天文地层学立足于天文学的地球轨道三要素的周期性和准周期性变化,可通过功率谱分析和数字滤波等信号处理与运算,进行地层划分与对比。层序地层学立足于海水进退的沉积间断,以不整合面和与之对应的整合面为边界的层序是其主要研究对象。从这一角度来讲,天文地层学虽源于旋回地层学[3],但它专门强调米兰科维奇周期作为内在因素,即只关注地球轨道参数变化驱动下形成的旋回地层。广义上说的“旋回”或层序地层学中的“旋回”更多地强调了地层的周期或规律性重复特征,忽略了其时间尺度含义,恰恰“天文”一词本身具有时间尺度含义,更强调了其代表的时间域意义。
3 天文地层学的研究意义及其发展方向 3.1 测井资料在天文地层学研究中的作用研究天文地层学的关键是从地层中识别米兰科维奇旋回,而识别米兰科维奇旋回的关键是从地层记录中选择能够反映过去气候变化的各类地球物理与地球化学等参数作为旋回的代替指标[9]。利用露头、岩心、古生物等资料开展地层周期及沉积旋回识别研究,往往受限于岩心来源、取样收获率等因素,很难做到连续采样,以进行系统的分析化验和岩石物理实验,而地震资料的分辨率又不够高,这为利用岩心和地震资料对复杂岩性地层,尤其是厚层泥页岩地层的高分辨率沉积旋回识别及划分带来了较大的局限性。在许多用于地层旋回分析的替代性指标中,测井曲线无疑是进行天文地层学分析的理想指标之一。不同测井曲线虽然对地层物理特征敏感程度不同,但所反映的地层沉积旋回是一致的[29]。据文献[30]报道,Milankovitch是以米级旋回为基本研究单位,这也恰好落在测井分辨率的范围内,这样,分析米兰科维奇周期就可以解释测井曲线代表的沉积剖面,这是测井曲线识别米兰科维奇周期的基础。
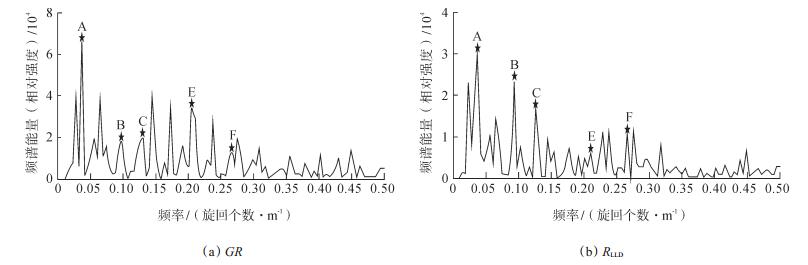
地球轨道的周期性变化必定引起气候的变化,并被记录在沉积地层中,这种变化会体现在岩性、岩相的变化上,并被测井曲线所记录[30]。不同规模和尺度的地层周期以及沉积单元的特征与变化,都会引起地层物理性质呈现不同的特征及差异,在测井曲线上表现为不同的幅度、形态及频率特征[31]。识别地层中米兰科维奇旋回信息的关键就是对时间序列进行频谱分析[9],自天文地层学建立以来,许多学者采取了多种方法对地层中的米兰科维奇旋回信息进行提取,主要是利用傅里叶和小波变换等对测井曲线进行时频分析,实现多尺度、多分辨率信号分解[32-33]。同时,为消除噪音的干扰,还要对原始数据进行数字滤波,以便提取剖面中的优势周期。张海峰等[34]利用米兰科维奇旋回地层学的理论基础,对东营凹陷沙四上亚段地层进行研究,在频率域上对比地球轨道理论模型与地质记录之间的关系,寻找两者之间的线性关系,从而识别出米兰科维奇旋回可作为天然时间标尺,并进一步建立了地层格架;李凤杰等[29]利用Matlab平台提供的快速傅里叶变换,对川东北地区上二叠统长兴组的测井曲线进行频谱分析(图 4),其主频周期及主频周期之比均具有良好的一致性,并证实该区长兴组中保存了米兰科维奇旋回。因此,许多学者的研究表明,高分辨率的测井信息能够在天文地层旋回研究中发挥关键作用。
|
下载eps/tif图 图 4 四川盆地东北部长兴组自然伽马和深侧向测井曲线的频谱分析(毛坝2井)[30] Fig. 4 Spectrum analysis of GR and RLLD curves of Changxing Formation in northeastern Sichuan Basin |
(1)有助于建立天文年代标尺
天文地层学因其较强的理论性和实际可操作性而不断发展。利用米兰科维奇旋回理论进行地质年代标定的方法被认为是地层学解读时间的第三里程碑[10]。进入21世纪,国际地层学一个重要进展是提出了天文(地质)年代表、天文年代学等概念,并把天文学中的地球轨道要素方法作为“国际地质年表”中确定年龄的重要方法之一,这说明天文地层因素已被正式应用于地层工作中,用以确定地质年代[3]。汪品先[35]也指出地球轨道参数的变化是地质尺度上唯一可以精确定量计算的周期现象,可用作地质计时的标尺。
天文地层学研究有助于认识地球轨道参数改变所诱发的气候变化、沉积旋回及生物演替等,通过对高分辨率旋回地层记录进行天文调谐来建立天文年代标尺,可以弥补缺少同位素测年依据的不足,为解决地质学领域的地层年代划分问题提供一种有效的手段。特别在最近几年,天文地层学研究在地质年代校正方面取得了突破性进展,已成为现代地质学研究的一个新的亮点[9]。所谓天文调谐就是指将沉积记录或古气候变化的替代性指标直接标定到偏心率、黄赤交角、岁差或日照量变化曲线上[20]。2004年公布的国际地质年表(GTS 2004)中提到,在新生代、早白垩世、早侏罗世和晚三叠世已成功地把地球轨道因素应用到地质年代的划分和对比中[36]。可见开展天文地层学研究有助于建立更完整、精细的天文年代标尺。
(2)有助于提高地层划分的时间分辨率
地层的精细划分一直是地层学关注的重点,传统的生物地层和岩石地层划分只能将地层划分到百万年级别,这远远不能满足现今非常规油气勘探与开发的需要,如何在原有的地质年代格架基础上进一步对地层进行精细年代划分,这是当前地层学研究面临的一个亟待解决的问题。许多重大地质学问题的解决均依赖于地质时间分辨率的提高,随着人类生产生活需求的不断提高,没有高分辨率的地质时间坐标,就不可能有与时间相关的高水平的地质学研究成果[37]。天文地层学是天文学与地质学的交叉学科,因其固有的天文成因机制,在地层界线年龄确定方面表现出明显的优势。地层中的旋回性沉积记录显示地层中的沉积节律明显受到天文周期的控制和驱动,在年代地层和生物地层框架内,地层记录中发现的米兰科维奇旋回信息所代表的时间涵义是进行高分辨率地层划分的有效手段[3]。此外,米兰科维奇旋回具有时间特性,可以对地层实现连续标定,从而可以测定地层单元的延续时间,从实际应用结果来看,其精度要远高于现行的生物地层学对比及同位素测年法。根据地层记录中米兰科维奇旋回的个数,能估算出地层堆积作用的绝对年限,有利于开展陆相地层的精细划分与研究。由于天文地层学主要是以受地球轨道周期性变化的地层旋回为研究对象,来确定地层的年龄值,因此可实现比阶更高级别的年代地层划分。
(3)能够为精确年代对比提供依据
尽管地球轨道变化对气候波动的诱发机制还不甚明了,但由于气候变化所导致的全球性周期沉积地层在大区域甚至在全球范围内均具有较好的等时性和侧向连续性,这为进行盆地内及盆地间的地层对比提供了新的可能性[38]。Connolly等[39]对亚利桑那州东南部的Pedregosa盆地中2条剖面进行盆内对比,得到了很好的对比结果,之后他们又将这2条剖面与相距1 500 km的中部大陆(堪萨斯州)上的1条剖面进行盆间对比,发现这3条剖面的主要界限具有很好的对应性,而且其精度远远高于生物地层对比结果。这也表明,开展天文地层学研究能够为盆地间(或更广地区间)地层年代精确对比提供更科学的依据。
3.3 天文地层学的发展方向(1)亚米兰科维奇旋回(ka级别)
米兰科维奇旋回是米兰科维奇效应在地层记录中的表现形式,地层记录中发现的米兰科维奇旋回、亚米兰科维奇旋回所代表的时间涵义是进行高分辨率地层旋回划分与对比的依据,尤其是小于米兰科维奇岁差周期(19 ka)的亚米兰科维奇旋回,可为地层的精确数字定年、含油气盆地地层成因机制和过程等研究提供新思路[3]。
以米兰科维奇理论为基础的天文地层学研究可将地层进行万年级别的高分辨率地层划分,但人们更希望得到与人类历史发展具有可对比性的千年级别甚至百年级别的地层旋回划分[40],传统的米兰科维奇理论显然已经不能够满足地层更小尺度(千年级别及百年级别)划分的需要,于是亚米兰科维奇周期的研究越来越受到人们的重视。近年来,亚米兰科维奇旋回对新生代以来大气和海洋系统的显著影响已经成为科学家的共识[41],亚米兰科维奇旋回的提出可以进一步将地层分辨率提高至千年级别甚至百年级别,这将把天文地层学研究提高到一个新的层次。
(2)厚层泥页岩地层的精细划分
随着非常规泥页岩油气勘探与开发的不断深入,细粒沉积研究越来越受到重视[42],而泥页岩环境,蕴含着地史演化过程中的丰富信息[43],较好地记录了天文地层周期及由于构造沉降、气候变迁和沉积物注入等因素而引起的沉积旋回变化。开展泥页岩地层周期及高分辨率沉积旋回研究,能够建立泥页岩地层的时间标尺,从而为泥页岩油气勘探与开发建立准确的地层时空坐标提供指导。
(3)系统的天文地层周期测井识别方法
利用连续、高分辨率的测井曲线来提取反映地层中的米兰科维奇旋回信息具有明显的优势,但目前还没有一套完整的系统评价方法来识别米兰科维奇旋回。目前,对测井数据的处理方法有以下几种,采用测井曲线滑动窗能谱分析识别地层中规则的高频旋回,并用来认识已知的米兰科维奇周期[44-45]。也有学者采用连续小波变换(CWT)与快速傅里叶变换联合的方法对自然伽马测井曲线进行分析,来开展高分辨率天文地层学研究,发现CWT的尺度因子α为12,24及60时分别与岁差、黄赤交角、偏心率的周期吻合较好[46]。王贵文等[47]提出利用最大熵谱分析法进行沉积旋回识别的研究方法,利用测井曲线功率谱分布图在纵向上的突变位置反映层序界面。目前,很少有人关注不同的时频分析方法与不同尺度天文周期、沉积单元之间的匹配关系,因此探索利用测井信号将偏心率、黄赤交角、岁差以及亚米兰科维奇旋回地层从深度域转换到时间域的方法,确立测井与万年级别和千年级别地层年代信息的转换关系,将地层地质年代标定到亚米兰科维奇周期,这将是天文地层学今后发展的一个方向。
4 结论(1)天文地层学的提出是为了突出地球轨道参数(偏心率、黄赤交角、岁差)对沉积物规律性变化的影响,天文地层学属于旋回地层学范畴,但又有其独特的内涵,它更强调引起地层周期旋回变化的驱动力是地球轨道参数的变化,是地层学中跨学科较多、研究较热的分支学科。
(2)天文地层学研究有助于建立更完整精细的天文年代标尺、有助于提高地质分层的时间分辨率、能够为精确年代对比提供更科学的依据。积极开展厚层泥页岩天文地层周期研究,有助于解决当前泥页岩油气勘探与开发在地质分层上所面临的难题。
(3)利用连续、高分辨率的测井曲线来研究天文地层学具有明显的优势,能够有效提取与地球轨道参数相关的地层响应信息。探索利用测井信息将不同尺度天文地层旋回从深度域到时间域的转换方法,结合测年资料将地层地质年代标定到亚米兰科维奇周期,这将是天文地层学今后发展的方向之一。
| [1] |
丁仲礼.
米兰科维奇冰期旋回理论:挑战与机遇. 第四纪研究, 2006, 26(5): 710.
DING Z L. 2006. The Milankovitch theory of pletstocene glacial cycles: challenges and chances. Quaternary Sciences (in Chinese), 2006, 26(5): 710. |
| [2] | HART M B. 1987. Orbitally induced cycles in the chalk facies of the United Kingdom. Cretaceous Research, 1987, 8(4): 335. DOI:10.1016/0195-6671(87)90003-6 |
| [3] |
徐道一, 韩延本, 李国辉, 等.
天文地层学的兴起. 地层学杂志, 2006, 30(4): 323–324.
XU D Y, HAN Y B, LI G H, et al. 2006. The rise of astrostratigraphy. Journal of Stratigraphy (in Chinese), 2006, 30(4): 323-324. |
| [4] |
姚益民, 徐道一, 张海峰, 等.
山东东营凹陷新生代天文地层表简介. 地层学杂志, 2007, 31(Suppl 2): 427.
YAO Y M, XU D Y, ZHANG H F, et al. 2007. A brief introduction to the Cenozoic astrostratigraphic time scale for the Dongying Depression, Shandong. Journal of Stratigraphy (in Chinese), 2007, 31(Suppl 2): 427. |
| [5] |
徐道一, 张海峰, 韩延本, 等.
陆相沉积的天文地层研究方法简介——以井下地层为例. 地层学杂志, 2007, 31(Suppl 2): 431–432.
XU D Y, ZHANG H F, HAN Y B, et al. 2007. Introduction to the method for the astrostratigraphic study of terrestrial sediments: taking underground stratigraphy for an example. Journal of Stratigraphy (in Chinese), 2007, 31(Suppl 2): 431-432. |
| [6] |
陈中红, 查明, 金强.
自然伽马及自然伽马能谱测井在沉积盆地古环境反演中的应用. 地球物理学报, 2004, 47(6): 1145.
CHEN Z H, ZHA M, JIN Q. 2004. Application of natural gamma ray logging and natural gamma spectrometry logging to recovering paleoenvironment of sedimentary basin. Chinese Journal of Geophysics (in Chinese), 2004, 47(6): 1145. |
| [7] | RAMPINO M R, PROKOPH A, ADLER A. 2000. Tempo of the end-Permian event:high-resolution cyclostratigraphy at the Permian-Triassic boundary. Geology, 2000, 28(7): 645. |
| [8] | BERGER A, LOUTRE M F, LASKAR J. 1992. Stability of the astronomical frequencies over the Earth's history for paleoclimatestudies. Science, 1992, 255(5044): 562. |
| [9] |
吴怀春, 张世红, 冯庆来, 等.
旋回地层学理论基础、研究进展和展望. 地球科学——中国地质大学学报, 2011, 36(3): 410.
WU H C, ZHANG S H, FENG Q L, et al. 2011. Theoretical basis, research advancement and prospects of cyclostratigraphy. Earth Science—Journal of China University of Geosciences (in Chinese), 2011, 36(3): 410. |
| [10] |
龚一鸣, 杜远生, 童金南, 等.
旋回地层学:地层学解读时间的第三里程碑. 地球科学——中国地质大学学报, 2008, 33(4): 446.
GONG Y M, DU Y S, TONG J N, et al. 2008. Cyclostratigraphy:the third milestone of stratigraphy in understanding time. Earth Science— Journal of China University of Geosciences (in Chinese), 2008, 33(4): 446. |
| [11] | VAIL P R, MITCHUM R M, THOMPSON III S. 1977. Seismic stratigraphy and global changes of sea level, part 3:relative changes of sealevel from coastal onlap. AAPG Memoir 26, 1977: 63. |
| [12] | CROSS T A, GARDNER M H. 1991. Base-Level Concepts and Sequence Stratigraphy. Research Program in Finance Working Papers, 1991. |
| [13] |
梅冥相, 徐德斌, 周洪瑞.
米级旋回层序的成因类型及其相序组构特征. 沉积学报, 2000, 18(1): 46–48.
MEI M X, XU D B, ZHOU H R. 2000. Genetic types of meter-scale cyclic sequences and their fabric features of facies-succession. Acta Sedimentologica Sinica (in Chinese), 2000, 18(1): 46-48. |
| [14] |
徐道一.
天文地质年代表与旋回地层学研究进展. 地层学杂志, 2005, 29(Suppl 1): 635.
XU D Y. 2005. Astro-geologic time scale and the advancements of cyclostratigraphy. Journal of Stratigraphy (in Chinese), 2005, 29(Suppl 1): 635. |
| [15] | HAYS J D, IMBRIE J, SHACKLETON N J. 1976. Variations in the Earth's orbit:pacemaker of the ice ages. Science, 1976, 194: 45-46. DOI:10.1126/science.194.4260.45 |
| [16] |
龚一鸣, 张克信.
地层学基础与前沿. 武汉: 中国地质大学出版社, 2007.
GONG Y M, ZHANG K X. Basic and frontiersinstratigraphy (in Chinese) . Wuhan: China University of Geosciences Press, 2007. |
| [17] | HILGEN F, SCHWARZACHER W, STRASSER A. 2004. Concepts and definitions in cyclostratigraphy (second reportof the cyclostratigraphy working group). SEPM Special Publication, 2004(81): 303-305. |
| [18] |
田军, 汪品先, 成鑫荣, 等.
南海ODP1143站上新世至更新世天文年代标尺的建立. 地球科学——中国地质大学学报, 2005, 30(1): 33–35.
TIAN J, WANG P X, CHENG X R, et al. 2005. Establishment of the Plio-Pleistocene astronomical timescale of ODP site 1143, southern south China Sea. Earth Science—Journal of China University of Geosciences (in Chinese), 2005, 30(1): 33-35. |
| [19] | ZACHOS J C, SHACKLETON N J, REVENAUGH J S, et al. 2001. Climate response to orbital forcing across the Oligocene-Miocene boundary. Science, 2001, 292: 274-278. DOI:10.1126/science.1058288 |
| [20] |
黄春菊.
旋回地层学和天文年代学及其在中生代的研究现状. 地学前缘, 2014, 21(2): 49–52.
HUANG C J. 2014. The current status of cyclostratigraphy and astrochronology in the Mesozoic. Earth Science Frontiers (in Chinese), 2014, 21(2): 49-52. |
| [21] |
付斌, 杨映洲, 邹丽蓉.
时频分析方法在识别河流相层序中的应用. 岩性油气藏, 2013, 25(4): 90.
FU B, YANG Y Z, ZOU L R. 2013. Application of time-frequency analysis technique to recognition of fluvial faciessequence. Lithologic Reservoirs (in Chinese), 2013, 25(4): 90. |
| [22] |
刘立, 薛林福.
旋回地层学的基本原理与研究方法. 世界地质, 1994, 13(3): 88.
LIU L, XUE L F. 1994. Fundamental principles and research methods of cyclostratigraphy. Global Geology (in Chinese), 1994, 13(3): 88. |
| [23] | SIERRO F J, LEDESMA S, FLORES J A, et al. 2000. Sonic and gamma-ray astrochronology:cycle to cycle calibration of Atlantic climatic records to Mediterranean sapropels and astronomical oscillations. Geology, 2000, 28(8): 695-697. DOI:10.1130/0091-7613(2000)28<695:SAGACT>2.0.CO;2 |
| [24] |
龚一鸣, 徐冉, 汤中道, 等.
广西上泥盆统轨道旋回地层与牙形石带的数字定年. 中国科学D辑:地球科学, 2004, 34(7): 641–642.
GONG Y M, XU R, TANG Z D, et al. 2004. The Upper Devonian orbital cyclostratigraphy and numerical dating conodont zones from Guangxi, South China. Science in China Series D:Earth Sciences (in Chinese), 2004, 34(7): 641-642. |
| [25] |
姚益民, 付国斌, 徐道一, 等.
新疆吐哈盆地侏罗系旋回地层的初步研究. 地层学杂志, 2003, 27(2): 123–127.
YAO Y M, FU G B, XU D Y, et al. 2003. Preliminary study on the high-resolution cyclostratigraphy of the Jurassic System in Turpan-Hami Basin, Xinjiang. Journal of Stratigraphy (in Chinese), 2003, 27(2): 123-127. |
| [26] |
刘洋, 吴怀春, 张世红, 等.
珠江口盆地珠一坳陷韩江组—万山组旋回地层学. 地球科学——中国地质大学学报, 2012, 37(3): 411–419.
LIU Y, WU H C, ZHANG S H, et al. 2012. Cyclostratigraphy research on the Hanjiang-Wanshan Formations in Zhuyi Depression, Pearl River Mouth Basin. Earth Science—Journal of China University of Geosciences (in Chinese), 2012, 37(3): 411-419. |
| [27] | LASKAR J, FIENGA A, GASTINEAU M, et al. 2011. La 2010:a new orbital solution for the longterm motion of the Earth. Physics, 2011, 532(2): 1-16. |
| [28] |
姚益民, 修申成, 魏秀玲, 等.
东营凹陷下第三系ESR测年研究. 油气地质与采收率, 2002, 9(2): 31.
YAO Y M, XIU S C, WEI X L, et al. 2002. Researches on the ESR geochronometry in Palaeogene of Dongyingdepression. Petroleum Geology and Recovery Efficiency (in Chinese), 2002, 9(2): 31. |
| [29] |
李凤杰, 郑荣才, 罗清林, 等.
四川盆地东北地区长兴组米兰科维奇周期分析. 中国矿业大学学报, 2007, 36(6): 806–809.
LI F J, ZHENG R C, LUO Q L, et al. 2007. Analysis of Milankovitch Cycles of the Changxing Formation in Northeastern Sichuan Basin. Journal of China University of Mining & Technology (in Chinese), 2007, 36(6): 806-809. |
| [30] |
李庆谋.
测井曲线Milankovitch周期分析与应用. 地球物理学报, 1996, 39(5): 699.
LI Q M. 1996. The analysis and application of Milankovitch cycles by logging data. Chinese Journal of Geophysics (in Chinese), 1996, 39(5): 699. |
| [31] |
余继峰, 李增学.
测井数据小波变换及其地质意义. 中国矿业大学学报, 2003, 32(3): 337–338.
YU J F, LI Z X. 2003. Wavelet transform of logging data and its geological significance. Journal of China University of Mining & Technology (in Chinese), 2003, 32(3): 337-338. |
| [32] |
冯磊.
利用地震资料时频特征分析沉积旋回. 岩性油气藏, 2011, 23(2): 95.
FENG L. 2011. Using time-frequency characteristics to analyze sedimentary cycle. Lithologic Reservoirs (in Chinese), 2011, 23(2): 95. |
| [33] |
付文钊, 余继峰, 杨锋杰, 等.
测井记录中米氏旋回信息提取及其沉积学意义——以济阳坳陷区为例. 中国矿业大学学报, 2013, 42(6): 1027.
FU W Z, YU J F, YANG F J, et al. 2013. Feature extraction of Milankovitch cycle in well logs and its sedimentological significance: a case study of Jiyang Depression zone. Journal of China University of Mining & Technology (in Chinese), 2013, 42(6): 1027. |
| [34] |
张海峰, 张林晔, 姚益民, 等.
东营凹陷沙河街组四段滩坝砂米氏旋回层序划分与对比. 地层学杂志, 2008, 32(3): 278–282.
ZHANG H F, ZHANG L Y, YAO Y M, et al. 2008. Milankovitch cycles and sequence division and correlation of the member 4 of the Shahejie Formation in the DongyingDepression, Shandong. Journal of Stratigraphy (in Chinese), 2008, 32(3): 278-282. |
| [35] |
汪品先.
地质计时的天文"钟摆". 海洋地质与第四纪地质, 2006, 26(1): 1.
WANG P X. 2006. Astronomical"pendulum"for geological clock. Marine Geology & Quaternary Geology (in Chinese), 2006, 26(1): 1. |
| [36] | GRADSTEIN F M, OGG J G, SMITH A G, et al. 2004. A new geologic time scale, with special reference to Precambrian and Neogene. Episodes, 2004, 27(2): 83-100. |
| [37] |
龚一鸣, 李保华.
高分辨率地层学与Milankovitch旋回和ENSO事件沉积. 地质科技情报, 1999, 18(2): 32.
GONG Y M, LI B H. 1999. High resolution stratigraphy, Milankovitch cycle and ENSO event deposits. Geological Science and Technology Information (in Chinese), 1999, 18(2): 32. |
| [38] |
吴智勇, 姜衍文.
地层记录中的天文事件及其研究意义. 岩相古地理, 1996, 16(4): 63–64.
WU Z Y, JING Y W. 1996. Astronomical events in the stratigraphic records and their implications. Sedimentary Facies and Palaeogeography (in Chinese), 1996, 16(4): 63-64. |
| [39] | CONNOLLY W M, STANTON R J. 1992. Interbasinalcyclostratigraphic correlation of Milankovitch band transgressive-regressive cycles:correlation of Desmoinesian-Missourian strata between southeastern Arizona and the midcontinent of North America. Geology, 1992, 20(11): 999-1002. DOI:10.1130/0091-7613(1992)020<0999:ICCOMB>2.3.CO;2 |
| [40] |
汪品先, 翦知湣.
寻求高分辨率的古环境记录. 第四纪研究, 1999, 19(1): 1–2.
WANG P X, JIAN Z M. 1999. Searching high-resolution paleoenvironmental records:a review. Quaternary Sciences (in Chinese), 1999, 19(1): 1-2. |
| [41] | RIAL J A. 1999. Pacemaking the ice ages by frequency modulation of Earth's orbital eccentricity. Science, 1999, 285: 565-567. |
| [42] |
姜在兴, 梁超, 吴靖, 等.
含油气细粒沉积岩研究的几个问题. 石油学报, 2013, 34(6): 1031.
JIANG Z X, LIANG C, WU J, et al. 2013. Several issues in sedimentological studies on hydrocarbon-biaring fine-grained sedimentary rocks. Acta Petrolei Sinica (in Chinese), 2013, 34(6): 1031. DOI:10.7623/syxb201306001 |
| [43] |
朱光有, 金强, 周建林.
东营凹陷旋回式深湖相烃源岩研究. 地质科学, 2003, 38(2): 254.
ZHU G Y, JIN Q, ZHOU J L. 2003. Source rock characters of cyclic deep-lake facies in the DongyingDepression. Chinese Journal of Geology (in Chinese), 2003, 38(2): 254. |
| [44] |
张占松, 蔡道钢, 甘利灯.
用测井曲线能谱分析技术研究沉积速率. 江汉石油学院学报, 1999, 21(4): 18–20.
ZHANG Z S, CAI D G, GAN L D. 1999. Studying sedimentation rate by means of spectral analysis of logs. Journal of Jianghan Petroleum Institute (in Chinese), 1999, 21(4): 18-20. |
| [45] |
朱剑兵.
基于最大熵谱估计的沉积旋回划分方法探讨. 岩性油气藏, 2012, 24(2): 67–71.
ZHU J B. 2012. Division of sedimentary cycle sequences based on maximum entropy spectrum estimation. Lithologic Reservoirs (in Chinese), 2012, 24(2): 67-71. |
| [46] | YU J F, SUI F G, LI Z X, et al. 2008. Recognition of Milankovitch cycles in the stratigraphic record:application of the CWT and the FFT to well-log data. Journal of China University of Mining and Technology, 2008, 18(4): 594. DOI:10.1016/S1006-1266(08)60301-6 |
| [47] |
王贵文, 邓清平, 唐为清.
测井曲线谱分析方法及其在沉积旋回研究中的应用. 石油勘探与开发, 2002, 29(1): 93–95.
WANG G W, DENG Q P, TANG W Q. 2002. The application of spectral analysis of logs in depositional cycle studies. Petroleum Exploration and Development (in Chinese), 2002, 29(1): 93-95. |
 2017, Vol. 29
2017, Vol. 29



