2. 中国石油大庆油田有限责任公司 采油三厂, 黑龙江 大庆 163318
2. No. 3 Oil Production Plant, PetroChina Daqing Oilfield Com., Ltd., Daqing 163318, Heilongjiang, China
页岩的孔隙结构主要包括孔径 (孔隙直径) 分布与孔隙度2个方面的内容,直接影响页岩气的赋存方式及储量大小,是储层评价的重要指标[1-2]。页岩孔隙结构的表征方法主要包括三大类:地球物理测井法、流体注入实验法和图像观测法[3]。地球物理测井法以核磁共振 (NMR) 测井技术为代表,NMR测井能够在不受岩石骨架影响的情况下获取孔隙结构信息,但只能得到岩石孔径的分布趋势,需要比对流体注入实验结果才能给出岩石的真实孔径[4-6]。流体注入实验法主要包括高压压汞法、液氮法、GRI法及CO2法,是当前页岩孔隙结构表征的常用方法,该方法可以给出孔体积随孔径变化的曲线,从而定量描述孔体积与孔径的对应关系[7-8],但只能通过总结流体经过岩样后的表观性质变化,间接获取储集空间信息,无法对孔隙结构进行直观的识别[9]。图像观测法主要以扫描电镜 (SEM)、透射电镜 (TEM)、原子力显微镜 (AFM) 及纳米CT为代表,结合统计学理论,可以确定页岩储层孔隙的形状、面孔率、孔径分布及孔隙连通性等参数,从而建立对页岩储层结构的直观认识[10-11]。然而,图像观测法对微小孔隙结构缺乏有效的测算方法,准确读取页岩图像中的孔隙结构信息比较困难,且通过描述图像的面上信息,无法全面地展现页岩储层的空间结构特征,尚不能从页岩岩体的角度对孔隙结构进行有效表征[12]。因此,目前利用图像观测法研究页岩孔隙结构主要集中在孔隙的二维形态学定性刻画上,涉及页岩孔隙结构的三维定量化描述并不多见。
川南龙马溪组页岩是中国石油海相页岩气勘探开发示范区,该区页岩沉积厚度大,一般为40~ 250 m,分布稳定,基质微观孔隙和裂缝均较发育,其岩石学特征和物性参数均接近北美产气页岩,被认为是我国页岩气勘探开发的首选目标[13]。近年来,国内学者已经对该区页岩做了大量的地质调查研究,在地球化学、沉积环境、矿物成分、储层物性以及含气量等特征方面均取得了丰富的研究成果[14-15]。这些成果和认识主要集中在宏观层面的资源评价上,受实验条件和地质资料限制,对微观孔隙结构的研究还不够深入,并不能全面地展现该区页岩的储集空间特征。为深入研究川南龙马溪组页岩的微观孔隙结构,利用MATLAB自编程序识别页岩SEM二值图像,获取孔隙面积数据,拟合得到面孔率与孔隙面积的函数关系,并通过积分几何理论建立页岩二维图像面孔率与三维岩体孔隙度之间的换算模型,进而得到页岩孔隙度随孔径变化的函数关系,从而实现对川南龙马溪组页岩孔隙结构的三维定量化分析,探索出一种基于SEM图像观测的页岩孔隙结构三维定量化表征新方法。
1 数学模型建立岩体图像的平面信息蕴含其空间信息,如何建立起二者之间的联系,实现岩石孔隙结构的三维定量化表征,国内外学者做出了积极的探索。鞠杨等[16]、李建胜等[17]、Chalmers等[18]和Bagherzadeh等[19]均成功地利用二维图像信息实现了岩石孔隙结构的三维定量化表征,但都只是利用数值算法或经验公式借助计算机软件实现三维定量化表征,并未从理论上建立起岩石二维平面与三维空间之间的数量关系。笔者运用积分几何理论,从面和体2个角度计算同一物理量 (孔隙数),从而推导出了页岩面孔率与孔隙度之间的换算模型,从理论角度建立了岩石孔隙二维平面信息与三维空间信息之间的关系。
应用积分几何的前提是相关参数必须连续变化。页岩孔隙大量发育,且以纳米级孔为主,孔径在一定尺度范围内可视为连续分布,在平面图像上,孔隙面积亦为连续变化。页岩孔隙结构的这一特点,使其满足了积分几何理论的应用前提。下面通过数学方法来建立面孔率函数与孔隙度函数之间的换算模型。
设Q是页岩岩样 (假设为一个凸体),E是岩样Q的一个随机切面 (E截取Q的随机性保证了统计意义下的正确性,实际操作中不存在真正的随机,可以利用多次切面取平均达到随机的效果),则切面E所截的总孔隙数T可表示为
| $ T = \left\langle s \right\rangle h(\sigma ){\rm{d}}\sigma $ | (1) |
式中:〈s〉为切面E的平均面积期望值,m2;σ为孔隙面积,m2;h (σ) 为切面的面孔率函数;h(σ) dσ即为单位切面上、面积在σ与σ + dσ之间的平均孔隙数。
由于页岩孔隙多为纳米级微孔,因此可以假设孔隙为球体,则切面E中面积在σ与σ + dσ之间的孔隙数M可表示为
| $ M = p(\lambda )\nu H(\lambda ){\rm{d}}\lambda \varphi (\sigma, \lambda ){\rm{d}}\lambda $ | (2) |
式中:λ为孔径,m;ν为岩样Q的体积,m3;p(λ) 为切面E与截面孔隙的相交概率函数;H(λ) 为页岩孔隙度函数;H(λ) dλ为单位体积岩样内孔径在λ与λ + dλ之间的孔隙数;p(λ)νH(λ) dλ为与随机切面E相交的孔隙平均数;φ(σ,λ) 为切面E与孔隙相交平面中,切面面积在σ与σ + dσ之间的概率密度函数。
对式 (2) 中的λ进行积分,就可得到岩样Q与切面E相交截面的总孔隙数X,即
| $ X = \int_{{\lambda _0}}^{ + \infty } {p(\lambda )\nu H(\lambda )\varphi (\sigma, \lambda ){\rm{d}}\lambda } $ | (3) |
式中:λ0为最小孔径,m,取λ的最小值。
式 (1) 和式 (3) 分别是从面和体2个角度计算同一切面中的孔隙数,因此,式 (1) 和式 (3) 是相等的,即
| $ T = X $ | (4) |
整理式 (4) 可得到由积分几何方法建立的页岩孔隙度与面孔率之间的关系方程,即
| $ \int_{{\lambda _0}}^{ + \infty } {p(\lambda )\nu H(\lambda )\varphi (\sigma, \lambda ){\rm{d}}\lambda } = \left\langle s \right\rangle h(\sigma ){\rm{d}}\sigma $ | (5) |
为了方便对式 (5) 进行求解,可以假设岩样Q为一个标准球体,利用平面几何与积分方程做一些变换,推导出ν,λ0,〈s〉和φ(σ,λ) 的关系表达式。经过一系列的运算,将式 (5) 变换为阿贝尔积分方程,其标准形式为
| $ \int_{\sqrt {\frac{\sigma }{{\rm{\pi }}}} }^{ + \infty } {\frac{{H(\lambda )d\lambda }}{{{\rm{\pi }}{\lambda ^2}-\sigma }}} = \sqrt {\rm{\pi }} h(\sigma ) $ | (6) |
利用分数阶微积分[20]求解式 (6),由于篇幅限制,具体求解过程不做详细论述,最终求解得到孔隙度函数表达式为
| $ H(\lambda ) = {\rm{ }}2{\rm{\pi }}\lambda \int_{{\rm{\pi }}{\lambda ^2}}^{ + \infty } {\frac{{h\prime (\sigma )}}{{\sqrt {\sigma-{\rm{\pi }}{\lambda ^2}} }}} {\rm{d}}\sigma $ | (7) |
选取川南龙马溪组页岩进行SEM观察拍照,利用MATLAB自编程序将所得到的SEM图像转换为灰度图像,每一个像素点都具有各自的灰度值。灰度值越大,在图像中的颜色表现越白,即结构表面距离成像表面越近,越倾向于固体颗粒;相反,灰度值越小,则越倾向于孔隙。
采用二值化的方法提取孔隙结构信息,二值化算法为
| $ g(i, j) = \left\{ \begin{array}{l} 1\;\;f(i, j) \ge W\\ 0\;\;f(i, j) < W \end{array} \right. $ | (8) |
式中:f (i,j) 为像素点 (i,j) 的初始灰度值;g(i,j) 表示二值化后像素点 (i,j) 的灰度值;W为分割阈值。
灰度值大于或等于阈值W的像素点,其灰度均被重新设置为1;灰度值小于阈值W的像素点,其灰度均被重新设置为0。
据此可得到二值化黑白图像 (图 1)。其中,黑色像素点 (g = 0) 代表孔隙,白色像素点 (g = 1) 代表固体颗粒。

|
下载eps/tif图 图 1 SEM灰度图(a)和二值化图像(b) Fig. 1 Gray image (a) and binary image (b) of SEM |
像素点放大后是具有一定面积的微正方形,将像素点视为最小面积单元,图像大小则由像素点的个数来确定。每个孔隙包含一定数目的像素点,按包含像素点的多少 (孔隙面积大小),可以将孔隙分为单个像素点孔隙至多个像素点孔隙,自编程序对孔隙像素点进行识别,可以得到不同大小孔隙及其所对应的面孔率值,面孔率计算方程为
| $ {P_i} = \frac{{i{N_i}}}{N} \times {\rm{ }}100\% \;\;\;1 \le i \le k $ | (9) |
式中:i为孔隙占有的像素点数;Ni为占有i个像素点的孔隙个数;k为最大孔隙占有的像素点数;N为像素点总数;Pi为占有i个像素点的孔隙所贡献的面孔率值。
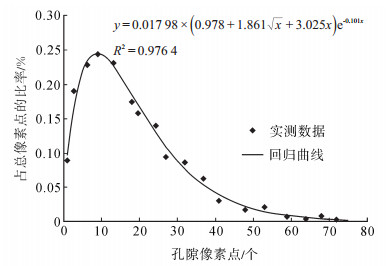
按照上述方法,在岩样上随机截取8个平面,每个平面随机观测10个点,获取80组观测数据。统计所有数据,得到不同大小孔隙的面孔率平均值,剔除一些奇异点,间隔抽样选取一组数据进行拟合,得到如图 2所示的拟合曲线。
|
下载eps/tif图 图 2 面孔率分布曲线 Fig. 2 Distribution curve of plane porosity |
将图 2中拟合所得的面孔率函数带入式 (6),得到页岩孔隙度随孔径变化的分布函数,即
| $ H(\lambda ) = {\rm{ }}0.072{\rm{ }}2\lambda {{\rm{e}}^{-0.101\lambda }} $ | (10) |
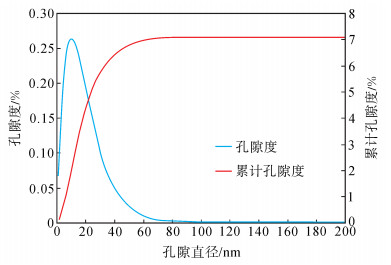
根据式 (10) 可得到孔隙度与累计孔隙度曲线 (图 3)。从图 3可以看出:孔隙度曲线表现为拟伽马分布,峰值出现在孔径为13 nm处,孔径主要为1~50 nm;累计孔隙度曲线在孔径为50 nm附近出现拐点,在50 nm之前较陡,在50 nm之后曲线趋于平缓。
|
下载eps/tif图 图 3 孔隙度与孔径关系曲线 Fig. 3 The relationship between porosity and pore size |
根据IUPAC (国际纯粹与应用化学联合会) 的划分标准[21],孔隙按孔径大小分为微孔、中孔和大孔3种类型。根据式 (10) 可计算出这3种类型孔隙各自的孔隙度贡献值、占总孔隙度的比例以及总孔隙度大小 (表 1)。由此可见,本次研究所选用的川南龙马溪组页岩岩样中的微孔和中孔较为发育,大孔较少,中孔是孔隙的主体,孔隙分布较为集中。
|
|
下载CSV 表 1 孔隙类型及其孔隙度贡献值 Table 1 Pore types and its porosity contribution value |
为验证SEM图像观测法所得结论的正确性,对页岩样品进行了流体注入实验分析。由于页岩超微孔隙的存在,单一流体注入无法全面表征页岩孔径分布范围,压汞法对渗透性极差的微小孔隙识别能力较弱,而氮气法对大孔隙的识别能力较弱[22],因此,分别进行了高压压汞实验和低温氮气吸附实验,综合二者的实验结果来分析SEM图像观测结论的正确性。
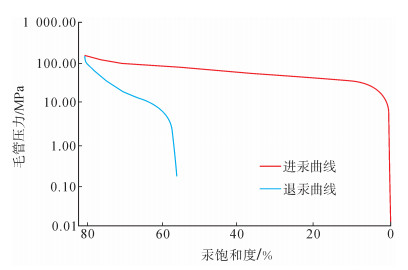
4.1 高压压汞实验选取同一页岩岩样,进行高压压汞实验,获得毛管压力曲线 (图 4),计算得到阈值压力大小为24.60 MPa。利用进汞量和注入压力之间的关系,根据Washburn方程求取孔喉半径,通过计算得到该页岩岩样的最大连通孔喉半径为29.88 nm,85%以上的进汞量集中在半径为4.4~15.6 nm的孔隙中,直径小于50 nm的孔隙占90%以上。该页岩岩样的主体孔隙半径分布较为集中,孔隙较小,以微孔、中孔为主。
|
下载eps/tif图 图 4 压汞毛管压力曲线 Fig. 4 Curves of mercury injection capillary pressure |
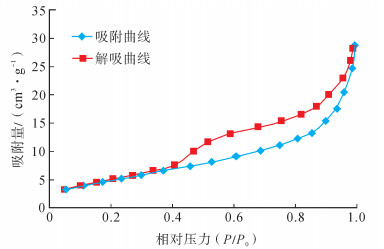
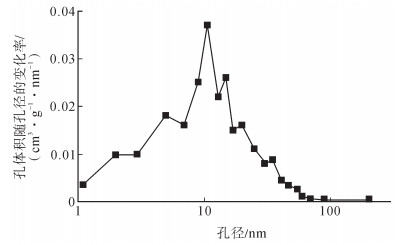
选取同一页岩岩样,进行低温氮气吸附实验。利用压力与吸附量的对应关系绘制氮气吸附-解吸曲线 (图 5)。根据BJH理论模型计算孔体积随孔径的变化,绘制孔径分布曲线 (图 6)。从图 6可以看出,该页岩岩样的孔体积主要为0.015~ 0.036 cm3/g,孔径主要为3~18 nm,孔径峰值出现在11 nm处,孔径分布集中,大孔较少,微孔、中孔是孔隙主体。
|
下载eps/tif图 图 5 页岩氮气吸附-解吸等温线 Fig. 5 Adsorption and desorption isotherms of nitrogen in shale |
|
下载eps/tif图 图 6 页岩孔径分布曲线 Fig. 6 Pore size distribution curve of shale |
根据SEM图像观测、高压压汞实验和低温氮气吸附实验所得数据,以10 nm为统计单元,分别计算了各段孔隙占总孔隙空间的比例 (表 2)。从表 2可以看出,3种方法获得的孔隙总体分布相近,孔径为10~20 nm的孔隙分布最多,孔径小于10 nm的次之,孔径大于20 nm的孔隙逐渐减少,孔径大于50 nm的孔隙分布最少。在孔径小于10 nm段,压汞法测试结果比SEM图像观测结果低6.2%;在孔径为10~20 nm段,2种方法所得结果接近;在孔径大于20 nm以后,压汞法所测结果均略高于SEM图像观测结果,在一定程度上反映出压汞法对微小孔隙的识别能力较弱。氮气法测试结果与SEM图像观测法结果在全部孔径段内均较相近。总体来说,SEM图像观测的结果与压汞实验、氮气吸附实验的结果在数值上均相近,分布趋势相同,表明了SEM图像观测法分析页岩孔隙结构的准确性。
|
|
下载CSV 表 2 不同大小孔隙占总孔隙空间的比例 Table 2 The proportion of different sizes of pores |
(1) 运用MATLAB自编程序识别页岩SEM二值图像的方法,获得了页岩面孔率与孔隙面积数据,拟合得到岩样面孔率与孔隙面积之间的函数关系。
(2) 利用积分几何理论建立了面孔率与孔隙度之间的换算模型,计算得到页岩孔隙度与孔径之间的函数关系,据此对龙马溪组页岩孔隙结构进行了定量分析。
(3) 川南龙马溪组页岩岩样的孔径主要为1~ 50 nm,孔隙度峰值出现在孔径为13 nm处,总孔隙度为7.07%,其中微孔、中孔、大孔分别占总孔隙空间的2.6%,93.7%和3.7%,中孔是孔隙的主体,孔隙分布较为集中。
(4) 对川南龙马溪组页岩岩样进行了高压压汞实验和低温氮气吸附实验,实验结果与SEM图像观测结果均较接近,验证了SEM图像观测法所得结果的准确性。
| [1] | ROSS D J K, BUSTIN R M. 2008. Characterizing the shale gas resource potential of Devonian-Mississippian strata in the western Canada sedimentary basin:application of an integrated formation evaluation. AAPG Bulletin, 2008, 92(1): 87-125. DOI:10.1306/09040707048 |
| [2] |
张金川, 林腊梅, 李玉喜, 等.
页岩气资源评价方法与技术:概率体积法. 地学前缘, 2012, 19(2): 184–191.
ZHANG J C, LIN L M, LI Y X, et al. 2012. The method of shale gas assessment:probability volume method. Earth Science Frontiers, 2012, 19(2): 184-191. |
| [3] |
顾忠安, 郑荣才, 王亮, 等.
渝东涪陵地区大安寨段页岩储层特征研究. 岩性油气藏, 2014, 26(2): 67–73.
GU Z A, ZHENG R C, WANG L, et al. 2014. Characteristics of shale reservoir of Da'anzhai segment in Fuling area eastern Chongqing. Lithologic Reservoirs, 2014, 26(2): 67-73. |
| [4] |
毛志强, 张冲, 肖亮.
一种基于核磁共振测井计算低孔低渗气层孔隙度的新方法. 石油地球物理勘探, 2010, 45(1): 105–109.
MAO Z Q, ZHANG C, XIAO L. 2010. A NMR-based porosity calculation method for low porosity and low permeability gas reservoir. Oil Geophysical Prospecting, 2010, 45(1): 105-109. |
| [5] | ABU-SHANAB M M, HAMADA G M, ORABY M E, et al. 2005. Improved porosity estimation in tight gas reservoirs from NMR and density logs. Emirates Journal for Engineering Research, 2005, 10(2): 9-13. |
| [6] |
王濡岳, 丁文龙, 王哲, 等.
页岩气储层地球物理测井评价研究现状. 地球物理学进展, 2015, 30(1): 228–241.
WANG R Y, DING W L, WANG Z, et al. 2015. Progress of geophysical well logging in shale gas reservoir evaluation. Progress in Geophysics, 2015, 30(1): 228-241. DOI:10.6038/pg20150134 |
| [7] |
何建华, 丁文龙, 付景龙, 等.
页岩微观孔隙成因类型研究. 岩性油气藏, 2014, 26(5): 30–35.
HE J H, DING W L, FU J L, et al. 2014. Study on genetic type of micropore in shale reservoir. Lithologic Reservoirs, 2014, 26(5): 30-35. |
| [8] |
杨峰, 宁正福, 孔德涛, 等.
高压压汞法和氮气吸附法分析页岩孔隙结构. 天然气地球科学, 2013, 24(3): 450–455.
YANG F, NING Z F, KONG D T, et al. 2013. Pore structure of shales from high pressure mercury injection and nitrogen adsorption method. Natural Gas Geoscience, 2013, 24(3): 450-455. |
| [9] |
张宪国, 张涛, 林承焰.
基于孔隙分形特征的低渗透储层孔隙结构评价. 岩性油气藏, 2013, 25(6): 40–45.
ZHANG X G, ZHANG T, LIN C Y. 2013. Pore structure evaluation of low permeability reservoir based on pore fractal features. Lithologic Reservoirs, 2013, 25(6): 40-45. |
| [10] | CURTIS M E, SONDERGELD C H, AMBROSE R J, et al. 2012. Microstructural investigation of gas shales in two and three dimensions using nanometer-scale resolution imaging. AAPG Bulletin, 2012, 96(4): 665-677. DOI:10.1306/08151110188 |
| [11] |
邹才能, 朱如凯, 白斌, 等.
中国油气储层中纳米孔首次发现及其科学价值. 岩石学报, 2011, 27(6): 1857–1864.
ZOU C N, ZHU R K, BAI B, et al. 2011. First discovery of nanopore throat in oil and gas reservoir in China and its scientific value. Acta Petrologica Sinica, 2011, 27(6): 1857-1864. |
| [12] | MONTGOMERY S L, JARVIE D M, BOWKER K A, et al. 2005. Mississippian Barnett Shale, Fort Worth Basin, north-central Texas:gas-shale play with multi-trillion cubic foot potential. AAPG Bulletin, 2005, 89(2): 155-175. DOI:10.1306/09170404042 |
| [13] |
王玉满, 董大忠, 李建忠, 等.
川南下志留统龙马溪组页岩气储层特征. 石油学报, 2012, 33(4): 551–561.
WANG Y M, DONG D Z, LI J Z, et al. 2012. Reservoir characteristics of shale gas in Longmaxi Formation of the Lower Silurian, southern Sichuan. Acta Petrolei Sinica, 2012, 33(4): 551-561. DOI:10.7623/syxb201204003 |
| [14] |
郭旭升, 李宇平, 刘若冰, 等.
四川盆地焦石坝地区龙马溪组页岩微观孔隙结构特征及其控制因素. 天然气工业, 2014, 34(6): 9–16.
GUO X S, LI Y P, LIU R B, et al. 2014. Characteristics and controlling factors of micro-pore structures of Longmaxi shale play in the Jiaoshiba area, Sichuan Basin. Natural Gas Industry, 2014, 34(6): 9-16. |
| [15] |
聂海宽, 张金川.
页岩气储层类型和特征研究——以四川盆地及其周缘下古生界为例. 石油实验地质, 2011, 33(3): 219–225.
NIE H K, ZHANG J C. 2011. Types and characteristics of shale gas reservoir:a case study of Lower Paleozoic in and around Sichuan Basin. Petroleum Geology and Experiment, 2011, 33(3): 219-225. DOI:10.11781/sysydz201103219 |
| [16] |
鞠杨, 杨永明, 宋振铎, 等.
岩石孔隙结构的统计模型. 中国科学, 2008, 38(7): 1026–1041.
JU Y, YANG Y M, SONG Z D, et al. 2008. Statistical model of pore structure of rock. Science in China, 2008, 38(7): 1026-1041. |
| [17] |
李建胜, 王东, 康天合.
基于显微CT试验的岩石孔隙结构算法研究. 岩土工程学报, 2010, 32(11): 1703–1708.
LI J S, WANG D, KANG T H. 2010. Algorithmic study on rock pore structure based on micro-CT experiment. Chinese Journal of Geotechnical Engineering, 2010, 32(11): 1703-1708. |
| [18] | CHALMERS G R, BUSTIN R M, POWER I M. 2012. Characterization of gas shale pore systems by porosimetry, pycnometry, surface area, and field emission scanning electron microscopy/ transmission electron microscopy image analyses:examples from the Barnett, Woodford, Haynesville, Marcellus, and Doig units. AAPG Bulletin, 2012, 96(6): 1099-1119. DOI:10.1306/10171111052 |
| [19] | BAGHERZADEH R, LATIFI M, NAJAR S S, et al. 2013. Threedimensional pore structure analysis of nano/microfibrous scaffolds using confocal laser scanning microscopy. Journal of Biomedical Materials Research Part A, 2013, 101(3): 765-774. |
| [20] | LIU C S. 2015. Counterexamples on Jumarie's two basic fractional calculus formulae. Communications in Nonlinear Science & Numerical Simulation, 2015, 22(1/2/3): 92-94. |
| [21] | MAYS T J. 2007. A new classification of pore sizes. Studies in Surfaceence & Catalysi, 2007, 160(7): 57-62. |
| [22] |
谢晓永, 唐洪明, 王春华, 等.
氮气吸附法和压汞法在测试泥页岩孔径分布中的对比. 天然气工业, 2006, 26(12): 100–102.
XIE X Y, TANG H M, WANG C H, et al. 2006. Contrast of nitrogen adsorption method and mercury porosimetry method in analysis of shale's pore size distribution. Natural Gas Industry, 2006, 26(12): 100-102. DOI:10.3321/j.issn:1000-0976.2006.12.026 |
 2017, Vol. 29
2017, Vol. 29



