致密砂岩气储层地质评价标准为:孔隙度 < 10%、原地渗透率 < 0.1 mD或空气渗透率 < 1 mD、孔喉半径 < 1 μm、含气饱和度 < 60% [1]。致密砂岩气储层具有孔隙结构复杂、岩性复杂、孔隙中油气水关系复杂等特征,导致岩石物理与测井曲线的响应缺乏规律,即有效储层与非储层、油气层与水层、高产气层与低产气层测井响应差别小。致密砂岩气储层评价的难点在于:测井响应复杂,储层孔隙度和渗透率均较低,地层骨架对测井信息的影响远大于孔隙流体的影响,测井资料对孔隙流体的分辨率低;储层非均质性严重,传统的测井解释模型及参数适用性有限等[2-3]。为了提高致密砂岩气储层测井解释的精度,目前国内外广泛应用核磁共振测井并结合密度测井或声波时差测井等来计算孔隙度及渗透率[4-5];油气田开发阶段测井资料以常规测井为主,一般利用中子-密度交会或岩性密度测井来研究岩性特征[3],利用三孔隙度重叠法、孔隙度背景值法、声波时差法等来识别气层[6],但这些方法在应用上都具有局限性。基于鄂尔多斯盆地延川南区块二叠系石盒子组的致密砂岩储层,在借鉴前人研究经验基础上,通过建立能够反映低渗透致密砂岩储层流体性质的含气指示参数,并利用多种参数的综合指示对气层进行有效识别;由于低孔、低渗储层孔隙结构复杂,使岩-电参数取值范围变大,因此采用变岩-电参数的Archie公式,计算致密砂岩储层的孔隙度、渗透率、饱和度,以期实现延川南区块致密砂岩气储层含气饱和度的高精度定量评价。
1 延川南区块概况及储层测井响应延川南区块位于鄂尔多斯盆地东南缘,本次研究的主要目的层 (三叠系石盒子组) 厚度大、砂体发育,为致密砂岩气的有利储层,岩性以细砂岩为主,岩性和物性共同控制了储层的含气性[7-8]。通过延川南区块7口井63块石盒子组砂岩岩心分析表明:孔隙度主要为4%~10%,渗透率主要为0.1~ 1.0 mD,反映石盒子组砂岩呈低孔、低渗特征。
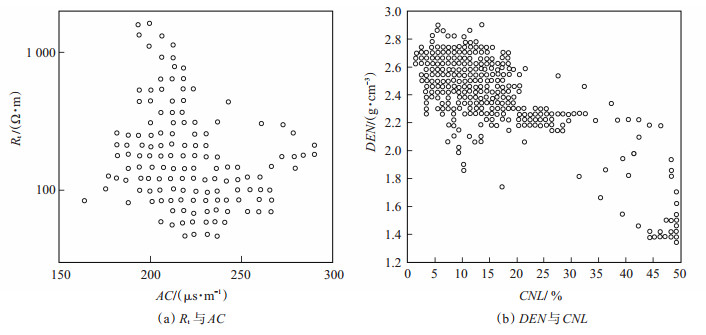
从延川南区块石盒子组储层测井响应特征分析 (图 1) 可以看出:石盒子组砂岩电阻率 (Rt) 呈中高值 (50~2 000 Ω·m)、声波时差 (AC) 呈中低值 (180~270 μs/m)、补偿密度 (DEN) 呈中高值 (2.3~ 2.7 g/cm3)、补偿中子 (CNL) 呈中低值 (3%~20%),反映储层岩性致密、物性较差。
|
下载eps/tif图 图 1 延川南区块石盒子组储层测井响应特征 Fig. 1 Log response characteristics of Shihezi Formation in the southern Yanchuan block |
对于中高孔、中高渗砂岩储层,利用气层与油层、水层测井响应特征的显著差异即可识别气层,但对于低渗透致密砂岩储层,由于其孔隙结构的复杂性使得孔隙中的流体对测井响应贡献小,气层识别难度较大[9]。由于油气田开发阶段测井资料以常规测井资料为主,因此需要提取多种参数进行气层识别。本文优选了基于常规测井资料的视弹性模量系数法和三孔隙度比值法,2种方法相结合进行综合分析,可以准确地识别气层。
2.1 视弹性模量系数法岩石的等效弹性模量定义为声阻抗乘以纵波速度。在相近的岩性和孔隙度条件下,气层声阻抗和纵波速度均比水层小,因此可以利用岩石等效弹性模量来识别流体性质。等效弹性模量为[10]
| $ M = {\rm{ }}{10^{15}}{\rho _b}/\Delta {t^2} $ | (1) |
式中:M为等效弹性模量,Pa;ρb为岩石密度,g/cm3;Δ t为声波时差,μs/m。
目的层完全含水时的等效弹性模量为
| $ {M^*} = \frac{{{{10}^{17}}[\varphi {\rho _{\rm{f}}} + (100{\rm{ }}-\varphi ){\rho _{{\rm{ma}}}}]}}{{{{[\varphi \Delta {t_{\rm{f}}} + (100{\rm{ }}-\varphi )\Delta {t_{{\rm{ma}}}}]}^2}}} $ | (2) |
式中:φ为地层孔隙度,%;ρf为孔隙流体密度,g/cm3;ρma为地层骨架密度,g/cm3;Δ tf为孔隙流体声波时差,μs/m;Δ tma为地层骨架声波时差,μs/m。
视弹性模量差比值Δ M [10]为
| $ \Delta M = ({M^*}-M)/M $ | (3) |
由式 (2) 与式 (3) 可知,地层完全含水时的M*大于完全含气时的M,因此地层含气时,Δ M = (M*-M)/M > 0,即:当Δ M > 0时指示为气层,反之为非气层。
2.2 三孔隙度比值法由于气层具有低密度、低中子、高声波时差响应特征,因此采用三孔隙度比值法来进行气层识别。
| $ \left\{ \begin{array}{l} {P_g} = ({\varphi _{\rm{D}}} + {\varphi _{\rm{S}}})/(2{\varphi _{\rm{N}}})\\ {\varphi _{\rm{D}}} = \varphi {'_{\rm{D}}}-{V_{{\rm{sh}}}}\frac{{{\rho _{{\rm{ma}}}}-{\rho _{{\rm{sh}}}}}}{{{\rho _{{\rm{ma}}}}-{\rho _{{\rm{mf}}}}}} = {\rm{ }}100\frac{{{\rho _{{\rm{ma}}}} - {\rho _{\rm{b}}}}}{{{\rho _{{\rm{ma}}}} - {\rho _{{\rm{mf}}}}}} - {V_{{\rm{sh}}}}\frac{{{\rho _{{\rm{ma}}}} - {\rho _{{\rm{sh}}}}}}{{{\rho _{{\rm{ma}}}} - {\rho _{{\rm{mf}}}}}}\\ {\varphi _{\rm{S}}} = \varphi {'_{\rm{S}}} - {V_{{\rm{sh}}}}\frac{{\Delta {t_{{\rm{sh}}}} - {\rm{ }}\Delta {t_{{\rm{ma}}}}}}{{\Delta {t_{{\rm{mf}}}} - {\rm{ }}\Delta {t_{{\rm{ma}}}}}} = 100\frac{{\Delta t - {\rm{ }}\Delta {t_{{\rm{ma}}}}}}{{\Delta {t_{{\rm{mf}}}} - {\rm{ }}\Delta {t_{{\rm{ma}}}}}} - {V_{{\rm{sh}}}}\frac{{\Delta {t_{{\rm{sh}}}} - {\rm{ }}\Delta {t_{{\rm{ma}}}}}}{{\Delta {t_{{\rm{mf}}}} - {\rm{ }}\Delta {t_{{\rm{ma}}}}}}\\ {\varphi _{\rm{N}}} = \varphi {'_{\rm{N}}} - {V_{{\rm{sh}}}}\frac{{{\Phi _{{\rm{Nma}}}} - {\Phi _{{\rm{Nsh}}}}}}{{{\Phi _{{\rm{Nma}}}} - {\Phi _{{\rm{Nmf}}}}}} = 100\frac{{{\Phi _{{\rm{Nma}}}} - {\Phi _{\rm{N}}}}}{{{\Phi _{{\rm{Nma}}}} - {\Phi _{{\rm{Nmf}}}}}} - {V_{{\rm{sh}}}}\frac{{{\Phi _{{\rm{Nma}}}} - {\Phi _{{\rm{Nsh}}}}}}{{{\Phi _{{\rm{Nma}}}} - {\Phi _{{\rm{Nmf}}}}}} \end{array} \right. $ | (4) |
式中:Pg为含气指示;φ'D与φD分别为泥质校正前、后补偿密度计算孔隙度,%;φ'S与φS分别为泥质校正前、后声波时差计算孔隙度,%;φ'N与φN分别为泥质校正前、后中子计算孔隙度,%;Vsh为泥质的体积分数,%;ρmf与ρsh分别为泥浆滤液、泥质的密度,g/cm3;Δ tmf与Δ tsh分别为泥浆滤液、泥质的声波时差,μs/m;ΦNma,ΦNmf与ΦNsh分别为纯砂岩骨架、泥浆滤液、泥质的中子值,%。
对于气层,φD > φN,φS > φN,Pg = (φD + φS)/ (2 φN) > 1,即:当Pg > 1时判别为气层,其值越大反映储层含气饱和度越高;Pg ≤ 1时判别为非气层。
3 致密砂岩储层参数评价 3.1 泥质含量泥质含量的求取精度直接影响着其他参数的求取精度,目前储层的泥质含量主要通过自然伽马、自然电位、自然伽马能谱等来求取[11]。对于致密砂岩储层,中子-密度交会是一种较好的计算方法,因为中子-密度交会对泥质灵敏且不受泥质分布和砂岩压实程度的影响,计算公式[2]为
| $ {V_{{\rm{sh}}}} = {\rm{ }}100(\varphi {'_{\rm{N}}}-\varphi {'_{\rm{D}}})/({\varphi _{{\rm{Nsh}}}}-{\varphi _{{\rm{Dsh}}}}) $ | (5) |
式中:φNsh与φDsh分别为泥岩的中子孔隙度和密度孔隙度,%。
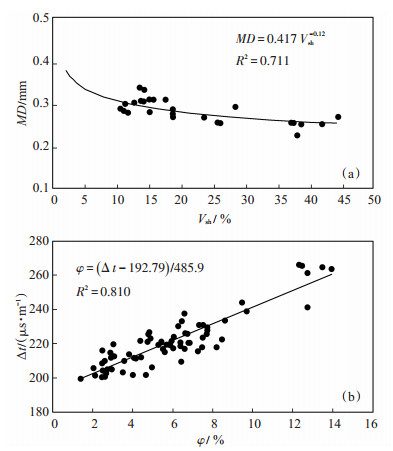
3.2 粒度中值岩心粒度中值与泥质含量回归[2]如图 2(a)所示,计算公式为
|
下载eps/tif图 图 2 粒度中值与泥质含量关系(a)及声波时差与孔隙度关系(b) Fig. 2 Relationship between median grain size and shale content (a) and relationship between AC and porosity (b) |
| $ MD = {\rm{ }}0.417V_{{\rm{sh}}}^{-0.12}, {R^2} = {\rm{ }}0.711 $ | (6) |
式中:MD为粒度中值,mm。
3.3 孔隙度岩心分析的孔隙度可以视作有效孔隙度,客观上要求测井解释的有效孔隙度应该与其保持一致[2]。对于含气储层,由于天然气的存在,引起视声波时差增大,密度与中子孔隙度均减小,因此可以使用中子-密度交会或中子-声波时差交会计算孔隙度,以消除天然气的影响[12]。
3.3.1 声波时差回归法实验分析孔隙度同声波时差曲线数据进行回归如图 2 (b) 所示,计算公式为
| $ \varphi = (\Delta t-{\rm{ }}192.79)/485.9, {R^2} = {\rm{ }}0.81 $ | (7) |
非气层段可用AC,DEN或CNL来计算孔隙度;气层段需先进行含气性校正,然后用中子-密度加权平均法[12]计算孔隙度
| $ \varphi = \frac{{{\varphi _{\rm{N}}} + {\varphi _{\rm{D}}}}}{4}{\rm{ }} + \sqrt {\frac{{\varphi _{\rm{D}}^2 + \varphi _{\rm{N}}^2}}{8}} $ | (8) |
以延川南区块延x井石盒子组致密砂岩为例 (图 3),与校正前的声波时差回归法计算的有效孔隙度相比,校正后的中子-密度加权平均法计算的有效孔隙度与岩心分析数据之间的误差更小,相对误差为3.49%,这是因为地层含气会使声波时差增大,声波时差回归法计算的孔隙度偏大,误差较大;中子-密度加权平均法可以消除气层的一部分影响,计算的孔隙度误差较小。因此,利用中子-密度加权平均法可以更准确地计算致密砂岩气储层的孔隙度。

|
下载eps/tif图 图 3 延x井石盒子组含气性校正前后的孔隙度对比 Fig. 3 Comparison of porosity before and after gas-bearing correction of Shihezi Formation in Yan x well |
渗透率是孔隙几何形状、孔喉直径、连通孔隙度等因素的函数,常规测井的每一种测井方法都不能唯一地反映岩石渗透率[11]。通过测井资料确定致密砂岩储层渗透率难度很大,一般可利用岩心分析数据建立孔隙度、粒度中值与渗透率的关系,进而确定渗透率。
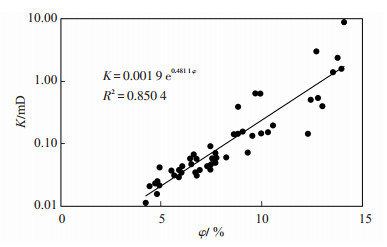
3.4.1 物性回归法延川南区块石盒子组岩心孔隙度、渗透率相关分析如图 4所示,计算公式为
|
下载eps/tif图 图 4 岩心渗透率与孔隙度相关分析 Fig. 4 Relationship between core permeability and porosity |
| $ K = {\rm{ }}0.001{\rm{ }}9{\rm{ }}{{\rm{e}}^{0.481{\rm{ }}1\varphi }}, {R^2} = {\rm{ }}0.850{\rm{ }}4 $ | (9) |
式中:K为渗透率,mD。
延川南区块石盒子组致密砂岩岩心分析渗透率与计算渗透率对比表明:本模型计算渗透率的误差较大,相对误差为64.48%,这一方面是因为目前无论测井计算还是实验分析获得的渗透率误差均较大;另一方面,这种模型主要适用于中高孔、中高渗储层,在低渗透致密砂岩储层中应用将加大误差。
3.4.2 粒度中值回归法利用岩心渗透率与粒度中值、孔隙度进行多元回归,计算公式为
| $ {\rm{lg}}K = {D_1} + {\rm{ }}1.7{\rm{ lg}}MD + {\rm{ }}7.11{\rm{ lg}}\varphi $ | (10) |
式中:D1为与砂岩的压实程度、胶结物含量和分选性有关的系数。
以延川南区块延1 x井石盒子组致密砂岩为例 (图 5),岩心分析渗透率与计算渗透率对比表明:本模型计算渗透率的误差较小,相对误差为12.4%,可更好地评价致密砂岩储层的渗透率。

|
下载eps/tif图 图 5 延川南区块延1 x井石盒子组测井孔隙度、渗透率与岩心分析对比 Fig. 5 Comparison of logging porosity, permeability and core data of Shihezi Formation of Yan 1x well in the southern Yanchuan block |
近年来的研究发现,对于低孔、低渗复杂储层,Archie公式的参数是可变的[2],尤其是m值的变化范围比较大,m值的变化对于油气层含水饱和度计算的影响最大。在应用Archie公式计算低孔、低渗储层含水饱和度时,岩-电参数根据目标区块地质特征来选取,主要是通过岩-电实验数据进行地层因素和饱和度指数分析,建立储层的岩-电关系,即变岩-电参数的饱和度模型,可有效克服储层性质多变对含水饱和度解释造成的影响[2]。
求取含水饱和度的Archie公式为
| $ {S_{\rm{w}}} = \sqrt[n]{{ab{R_{\rm{w}}}/({R_{\rm{t}}}{\varphi ^m})}} $ | (11) |
式中:Rw为地层水电阻率,Ω·m;Rt为地层电阻率,Ω·m;m为胶结指数;n为饱和度指数;a, b均为经验系数;Sw为含水饱和度,%。
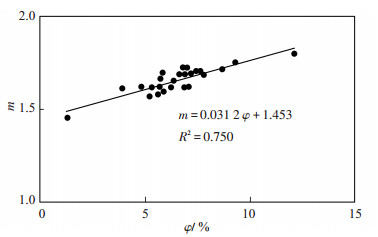
延川南区块石盒子组致密砂岩储层孔隙度低,地层因数F值分布发散且变化较大。令F = a/φm,当a = 1时,有m =-lg F/ lg φ。m的变化特征如图 6所示,m与φ呈线性正相关
|
下载eps/tif图 图 6 延川南区块石盒子组致密砂岩m与φ关系 Fig. 6 Relationship between m and φ of tight sandstone of Shihezi Formation in the southern Yanchuan block |
| $ m = {\rm{ }}0.031{\rm{ }}2\varphi + {\rm{ }}1.453, {R^2} = {\rm{ }}0.750 $ | (12) |
图 7为延川南区块延x井石盒子组储层综合评价图,常规测井曲线含气特征并不明显,P g和Δ M 对储层的含气性均有很好的识别能力,含气性好的储层P g与Δ M往往具有较好的一致性,而含气性差的储层通常会出现一方指示变弱的现象,以983.4~987.5 m气层段为例,P g最高达1.91,Δ M最高达0.3,含气特征明显;定量计算的MD为0.27~ 0.31 mm,为细—中砂岩,平均孔隙度为9.2%,平均渗透率为0.13 mD,利用变m值的Archie公式求取的平均含气饱和度为56.9%,测井综合评价为气层。该层段经压裂测试日产气0.67万m3。

|
下载eps/tif图 图 7 延x井石盒子组储层综合评价 Fig. 7 Comprehensive reservoir evaluation of Shihezi Formation in Yan x well |
位于鄂尔多斯盆地伊陕斜坡东北部大牛地地区的DPSx井,石盒子组、山西组、太原组均以细砂岩—中砂岩为主;储层物性较差,孔隙度普遍小于10%,岩性和物性共同控制了储层的含气性[13-14]。
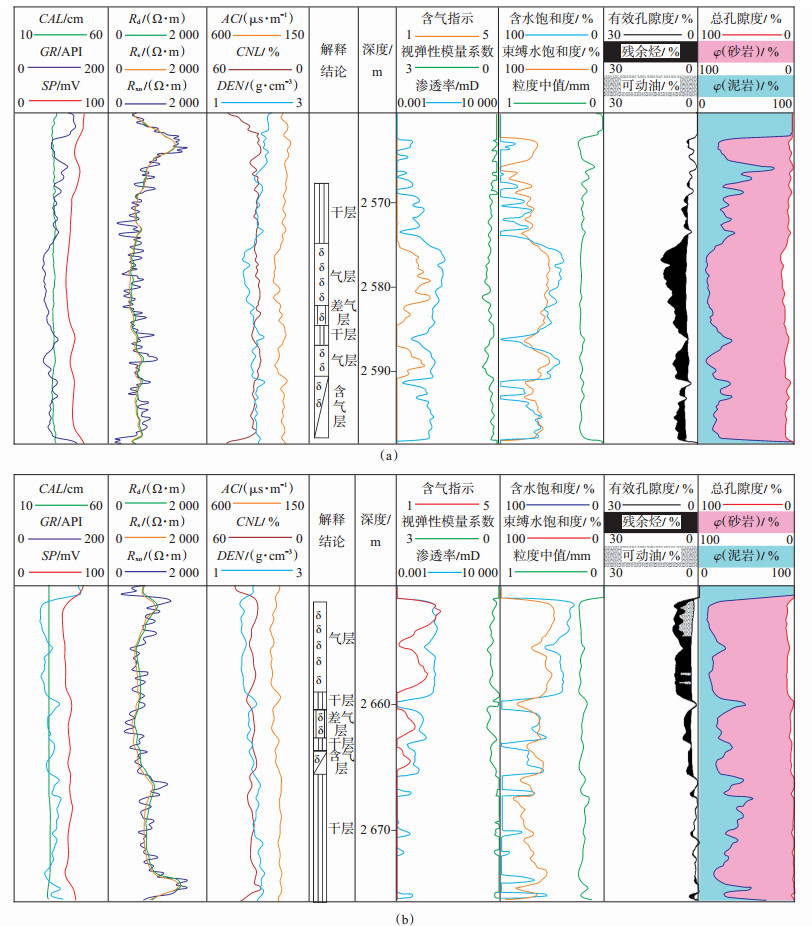
图 8为DPSx井石盒子组与山西组储层综合评价图,从测井曲线可以看出目的层砂体发育,厚度较大,电阻率曲线较平稳,从电性上很难区分含气性的好坏,但从综合处理成果上可以看出Pg和Δ M对储层的含气性有很好的识别能力,其幅度的大小指示含气的丰度,含气性越好二者对应关系也越好,特别是Pg对含气性更为敏感。2 575.2~ 2 582.8 m和2 651.0~2 658.3 m气层段经压裂测试日产气2.27万m3。
|
下载eps/tif图 图 8 DPSx井石盒子组(a)与山西组(b)储层综合评价 Fig. 8 Comprehensive reservoir evaluation of Shihezi Formation (a) and Shanxi Formation (b) in DPSx well |
综合图 7、图 8分析:利用Pg及Δ M识别气层效果很好,且二者结果具有较好的一致性。在埋藏深度较小、压实程度较低的地层,Pg对气层的指示效果更好 (图 7),P g值越大反映含气饱和度越高;在埋藏深度较大、压实程度较高的地层,Δ M对气层的反映更灵敏 (图 8),因此2种方法相结合,可更好地提高气层识别的准确度。
5 结论(1) 基于常规测井资料视弹性模量系数法和三孔隙度比值法,可以有效地识别气层,并在延川南区块低渗透致密砂岩气层识别中取得了较好的应用效果。
(2) 对于致密砂岩储层,中子-密度加权平均法计算的储层孔隙度比单独使用某一种孔隙度测井曲线计算的储层孔隙度更精确。(3) 粒度中值回归法相对于中高孔、中高渗储层的物性回归法可以更好地评价致密砂岩储层的渗透率。
(4) 变岩-电参数的Archie公式对致密砂岩气的评价具有较好的适用性,实现了延川南区块致密砂岩储层含气饱和度的高精度定量评价,展示出了良好的应用前景。
| [1] |
李建忠, 郭彬程, 郑民, 等.
中国致密砂岩气主要类型、地质特征与资源潜力. 天然气地球科学, 2012, 23(4): 607–608.
LI J Z, GUO B C, ZHENG M, et al. 2012. Main types, geological features and resource potential of tight sandstone gas in China. Natural Gas Geoscience, 2012, 23(4): 607-608. |
| [2] |
中国石油勘探与生产分公司.
低孔低渗油气藏测井评价技术及应用. 北京: 石油工业出版社, 2009: 104-117.
Petrochina Exploration & Production Company. Well logging evaluation technology and its application of low porosity and low permeability oil and gas reservoir (in Chinese) . Beijing: Petroleum Industry Press, 2009: 104-117. |
| [3] |
赵彦超, 吴春萍, 吴东平.
致密砂岩气层的测井评价——以鄂尔多斯盆地大牛地山西组一段气田为例. 地质科技情报, 2003, 22(4): 65–70.
ZHAO Y C, WU C P, WU D P. 2003. Logging evaluation to tight gas sandstone:a case study from the first member of Shanxi Formation in Daniudi gas pool, Ordos Basin, China. Geological Science and Technology Information, 2003, 22(4): 65-70. |
| [4] | ABU-SHANAB M M, HAMADA G M, ORABY M E, et al. 2005. Improved porosity estimation in tight gas reservoirs from NMR and density logs. Emirates Journal for Engineering Research, 2005, 10(2): 9-13. |
| [5] |
毛志强, 张冲, 肖亮.
一种基于核磁共振测井计算低孔低渗气层孔隙度的新方法. 石油地球物理勘探, 2010, 45(1): 105–109.
MAO Z Q, ZHANG C, XIAO L. 2010. A NMR-based porosity calculation method for low porosity and low permeability gas reservoir. Oil Geophysical Prospecting, 2010, 45(1): 105-109. |
| [6] |
曹延旭.
用测井方法识别致密砂岩天然气层. 石油仪器, 2005, 19(3): 63–64.
CAO Y X. 2005. Application of gas logging interpretation distinguishing technology in gas field. Petroleum Instruments, 2005, 19(3): 63-64. |
| [7] |
王伟力, 高海仁.
鄂尔多斯盆地中东部致密砂岩储层地质特征及控制因素. 岩性油气藏, 2013, 25(6): 71–77.
WANG W L, GAO H R. 2013. Geologic characteristics and controlling factors of tight sand reservoir in the mid-eastern Ordos Basin. Lithologic Reservoirs, 2013, 25(6): 71-77. |
| [8] |
侯加根, 唐颖, 刘钰铭, 等.
鄂尔多斯盆地苏里格气田东区致密储层分布模式. 岩性油气藏, 2014, 26(3): 1–6.
HOU J G, TANG Y, LIU Y M, et al. 2014. Distribution patterns of tight reservoirs in eastern Sulige Gas Field, Ordos Basin. Lithologic Reservoirs, 2014, 26(3): 1-6. |
| [9] |
李霞, 石玉江, 王玲, 等.
致密砂岩气层测井识别与评价技术——以苏里格气田为例. 天然气地球科学, 2013, 24(1): 62–68.
LI X, SHI Y J, WANG L, et al. 2013. Logging identification and evaluation technique of tight sandstone gas reservoirs:taking Sulige gas field as an example. Natural Gas Geoscience, 2013, 24(1): 62-68. |
| [10] |
孙小平, 石玉江, 姜英昆.
长庆低渗透砂岩气层测井评价方法. 石油勘探与开发, 2000, 27(5): 116.
SUN X P, SHI Y J, JIANG Y K. 2000. Log interpretation method for low permeability sandstone gas reservoir of Changqing gas field. Petroleum Exploration and Development, 2000, 27(5): 116. |
| [11] |
雍世和, 张超谟.
测井数据处理与综合解释. 东营: 中国石油大学出版社, 2007: 178-184.
YONG S H, ZHANG C M. Logging data processing and comprehensive interpretation (in Chinese) . Dongying: China University of Petroleum Press, 2007: 178-184. |
| [12] |
孙越, 李振苓, 郭常来.
致密砂岩气层测井评价方法研究. 科学技术与工程, 2012, 12(19): 4608.
SUN Y, LI Z L, GUO C L. 2012. Method research for logging evaluation of tight gas-bearing sandstone. Science Technology and Engineering, 2012, 12(19): 4608. |
| [13] |
吴娟娟, 李仲东, 陈威, 等.
大牛地气田太2段致密砂岩气层识别研究. 岩性油气藏, 2013, 25(1): 102–106.
WU J J, LI Z D, CHEN W, et al. 2013. Recognition of compacted sandstone gas reservoirs of Tai 2 member in Daniudi gas field. Lithologic Reservoirs, 2013, 25(1): 102-106. |
| [14] |
田方, 刘显明, 程玉梅.
鄂尔多斯盆地低渗透气藏测井解释技术. 测井技术, 1999, 23(2): 93–98.
TIAN F, LIU X M, CHENG Y M. 1999. Log interpretation technique for low-permeable gas reservoir in Eerduosi Basin. Well Logging Technology, 1999, 23(2): 93-98. |
 2017, Vol. 29
2017, Vol. 29



