运用地震叠前数据开展裂缝预测需宽(全)方位采集,这就成倍地增加了地震处理和解释的工作量,在低油价形势下,成本原因可能会限制其广泛应用。针对地震叠后数据,目前主要应用相干、曲率、倾角等开展单属性或多属性分析[1],以更好地解释构造裂缝,但它们反映小断裂和裂缝带并不明显。地震应力估算提供了一种趋势背景,地震裂缝预测中更多的是运用了场约束技术[2];蚂蚁追踪技术、IPA(Image Process and Analysis)技术以及时频域分析等[3-5],尽管它们均突出了地震叠后数据的多尺度效应,却无法展现其方向效应。
近年来,图像增强技术发展迅猛,并已逐步应用于地震数据的处理和解释工作中。Bondar[6]与Hesthammer[7]均尝试利用各种滤波技术来增强地震层位和断层的边界,可以认为是图像增强技术应用于地震构造解释的开始;陈凤等[8]与孙夕平等[9]均应用空间域各向异性扩散方法增强地震构造成像效果;杨宁等[10]尝试利用数学形态学理论增强地震图像中的构造信息。上述基于空间域的图像增强技术较好地反映了地震叠后数据的多尺度效应,但仍然不能反映方向效应。随着小波分析技术的发展,频率域图像增强技术受到广泛关注。石双虎[11]系统总结了频率域纵横波与裂缝尺度及各向异性的关系,Chapman[12]利用等效介质理论证明不同尺度裂隙各向异性与频率相关。Candès等[13]提出曲波变换后迅速应用于地震去噪、成像等处理。曲波变换研究证明,针对裂隙,纵波反射的高频能量在不同方向上具有不同的调谐效应,对应于时间域,则表现为在不同方向上的振幅能量分布不均,这为频率域图像增强技术应用于叠后地震裂缝各向异性检测奠定了理论基础。针对地震叠后数据,张广智等[14]利用曲波(Curvelet)变换具有各向异性的特点,首次提出了利用Curvelet变换预测裂缝带发育强度和走向的思路。
基于Contourlet变换的图像增强技术可运用于地震裂缝识别中,该技术不但具有多尺度的特点,而且可突出叠后数据的各向异性,具有速度快、冗余度小的优势,适合于低成本条件下的高精度地震裂缝预测。
1 基于Contourlet变换的图像增强技术图像增强指通过对图像信号的加工,使其从视觉效果上更加清晰或者突出了想要识别的特征[15]。目前,图像增强方法主要有频率域法和空间域法,基于Contourlet变换的图像增强技术属于频率域法范畴。
1.1 Contourlet变换基本原理Contourlet变换的基本思路是先采用拉普拉斯塔式滤波器(LP)直接对图像进行滤波,达到离散频率域多尺度分解的目的,得到1个低频和一系列高频子带信号,这些高频信号包含了不同尺度的边缘奇异点;然后利用方向滤波器组(DFB)对高频子带信号进行方向滤波,就可以将不同方向上的奇异点合成为不同的系数,不同方向的系数经过重构后在时间域表现为不同方向上图像的轮廓[16-18]。
LP首先要构建高斯金字塔,假设利用LP进行层分解,设第1层图像信号为原始灰度图像,则第l层高斯塔式图像信号Gl为
| $ \begin{array}{l} {\mathit{G}_\mathit{l}}{\rm{(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{) = }}\sum\limits_{\mathit{m}{\rm{ = - }}\mathit{M}}^\mathit{M} {\sum\limits_{\mathit{n}{\rm{ = - }}\mathit{N}}^\mathit{N} {\mathit{h}{\rm{(}}\mathit{m}{\rm{,}}\mathit{n}{\rm{)}}{\mathit{G}_{\mathit{l}{\rm{ - 1}}}}{\rm{(2}}\mathit{i}{\rm{ + }}\mathit{m}{\rm{,2}}\mathit{j}{\rm{ + }}\mathit{n}{\rm{),}}\;{\rm{2}} \le \mathit{l} \le \mathit{L}{\rm{,}}} } \\ \;\;\;\;\;\;\;\;\;\;{\rm{ - }}\mathit{M} \le \mathit{m} \le \mathit{M}{\rm{, - }}\mathit{N} \le \mathit{n} \le \mathit{N}{\rm{,0}} \le \mathit{i} \le \mathit{I}{\rm{,0}} \le \mathit{j} \le \mathit{J} \end{array} $ | (1) |
式中:h(m, n)是给定的M × N阶低通滤波窗口函数,相当于具有紧致支撑基的正交滤波器,M和N为所取窗口最大行、列数,通常取2,即m和n分别为计算时样点的行、列位置;L为最大层号;I和J分别为第l层图像的最大行、列数;i和j分别为灰度图像中的行、列位置。
Gk(i, j)是降采样后的结果,当M和N均取2时,其只有上层图像的1/4,需要内插后保持与前层图像信号大小一致。内插后图像记为Gl*(i, j),最终分解得到图像序列G1*, G2*, …, GL*。若用LPl-1表示拉普拉斯分解得到的第l -1层图像信号,则
| $ \left\{ \begin{array}{l} \mathit{L}{\mathit{R}_{\mathit{l}{\rm{ - 1}}}}{\rm{ = }}{\mathit{G}_{\mathit{l}{\rm{ - 1}}}}{\rm{ - }}\mathit{G}_{\rm{1}}^{\rm{*}}{\rm{, }}\;\;\;\;\;{\rm{1}} \le \mathit{l < L}\\ \mathit{L}{\mathit{P}_\mathit{l}}{\rm{ = }}{\mathit{G}_\mathit{L}}{\rm{, }}\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;l{\rm{ = }}L \end{array} \right. $ | (2) |
循环式(1)~(2)就可分解得到1个低频的图像信号LPl和各层高频信号LPl-1,完成频率域图像信号的多尺度分解。
针对每一层的高频图像信号,Contourlet变换利用DFB进行方向滤波,将频率域方向信号划分到理想精度,同时具有良好的图像重构性能。DFB方向滤波包括2个模块,第1个模块是构造平移算子进行平移操作,相当于对图像样本进行重新排序,通常利用如下对角形式的整体采样矩阵来实现对图像信号的数字平移采样
| $ \mathit{S}_\mathit{k}^\mathit{h} = \left\{ \begin{array}{l} {\rm{diag(}}{{\rm{2}}^{\mathit{h}{\rm{ - 1}}}}{\rm{, 2), }}\;\;\;\;\;\;0<k<{2^{\mathit{h} - 1}}\\ {\rm{diag(2, }}{{\rm{2}}^{\mathit{h}{\rm{ - 1}}}}{\rm{), }}\;\;\;\;\;\;{2^{\mathit{h} - 1}}<\mathit{k}<{2^\mathit{h}} \end{array} \right. $ | (3) |
式中:diag为创建的一个对角阵;k为在l层分解的方向数目,它是一个h级树形结构。第2个模块是采用具有菱形滤波功能的正交滤波器组进行频率分区,具有随尺度大小和不同方向而变化长宽比的“楔形”支撑基,使Contourlet变换在不同方向上的核函数不同。在某方向或完全重构图像时,需要再次利用平移算子对分区结果进行“逆采样”,以达到合成图像的目的。加了平移算子的“逆采样”合成矩阵为
| $ {\left\{ {\mathit{d}_\mathit{k}^\mathit{h}\left[{\mathit{b}{\rm{-}}\mathit{S}_\mathit{k}^\mathit{h}\mathit{c}} \right]} \right\}_{{\rm{0}} \le \mathit{k}{\rm{<}}{{\rm{2}}^\mathit{h}}{\rm{, }}\mathit{c} \in {\mathit{z}^{\rm{2}}}}} $ | (4) |
式中:b为第l层灰度图像的采样点数;c为第l层图像分解的方向数目;d表示“逆采样”合成矩阵。
式(4)表示的采样矩阵可以看成是一簇离散的支撑基,具有方向性和局部化的特征,利用该离散基可以将LP分解后的不同尺度图像按照需求合成,从而得到不同方向特征图像或者完全重构图像。假设λ(t)为某一方向上合成的图像,φ(t)为原始尺度分解后的图像,则
| $ \mathit{\lambda }_{\mathit{l, k, c}}^\mathit{h}\left( \mathit{t} \right){\rm{ = }}\sum\limits_\mathit{b} {\mathit{d}_\mathit{k}^\mathit{h}} \left[{\mathit{b}{\rm{-}}\mathit{S}_\mathit{k}^\mathit{h}\mathit{c}} \right]{\mathit{\varphi }_{\mathit{l, b}}}\left( \mathit{t} \right) $ | (5) |
式中:l和k分别体现了尺度和方向;b和c分别代表了合成与分解的采样大小。它们共同体现了计算的局部化特征。
1.2 Contourlet变换的优势Contourlet变换继承了Curvelet变换的多尺度和各向异性的特征,在某种意义上可以认为是对Curvelet变换的改进,但是与第2代Curvelet变换有如下区别[18-19]。
(1)实现过程不同。Curvelet变换采用函数逼近的形式将图像信号从连续域转换到离散域。Contourlet变换采用双滤波器迭代组合的方式直接在离散域定义函数。因此,Contourlet变换实现了在离散域的无缝转换,对于边界轮廓的显示在理论上具有更小的逼近误差。理论证明:Curvelet变换的误差衰减率为
(2)分解方式不同。Curvelet变换在极坐标下依照给定的尺度和角度采样计算,支撑基类似于同心圆中不同半径差和曲率弧构成的“楔形”。Contourlet变换在矩形网格算,支撑基类似于同中分割形成的“楔形”。
(3)“稀疏”程度不同。Curvelet变换类似于通过简单的旋转单个核函数来获得不同方向上的系数;Contourlet变换在不同尺度和不同方向上具有不同的核函数。因此,信号由离散频率域反变换重构图像时,Curvelet变换计算的冗余度达1+16 l(l是尺度分解的层数),而Contourlet变换计算的冗余度小于
基于Contourlet变换的图像增强技术在叠后裂缝预测中的应用主要分为3步来完成。
(1)设定分解尺度和分解方向的数目,针对地震叠后数据开展Contourlet变换,完成地震振幅的方向分解。
(2)将变换得到的不同方向的振幅分别计算相干,得到不同方向的相干体。
(3)将计算得到的各个方向的相干体进行融合,定性表征断裂和裂缝带的发育强度以及方向。融合算法中,样点的裂缝发育强度为
| $ F = 1 - {({\mathit{C}_\mathit{k}})_{min}}, \;\;\;\;\;1 \le k \le K $ | (6) |
式中:F为样点处裂缝发育强度;(Ck) min为样点在K个方向中相干系数最小的方向k的相干值。
由式(6)可以看出,F实质上是一个间接表征裂缝(带)发育强弱的指示因子,在断裂和裂缝不发育区域,相干值为1,此时F = 0。相干值最小表明在该方向上不连续性最强,这个方向可认为是裂缝(带)走向(D),可表示为
| $ D = 90/K + 180(\mathit{k} + 1)/\mathit{K} - \alpha $ | (7) |
式中:α为工区与正北方向的夹角。
2 地震物理模型正演 2.1 地震物理模型设计与采集针对某盆地工区致密灰岩储层实际地质背景设计模型(图 1),比例尺为1:10 000,物理模型大小为1.0 m×0.5 m。模型模拟3 000 m埋藏深度,地层有微弱起伏变化,发育4条断裂,断距较小且每条断裂断距变换不一;断裂伴生构造裂缝,裂缝发育带强弱不一;模型右上角设计4个不同的裂缝密度带,从左至右裂缝密度逐渐增大;模型上方设计7种不同走向、不同密度的交叉裂缝带。

|
下载eps/tif图 图 1 地震物理模型 Fig. 1 Seismic physics model |
地震物理模拟中采用三维数据采集方式,水层模拟上覆1 000 m地层,采取单发单收、双边放炮,面元参数为25 m × 25 m,覆盖次数为70次,主频达30 Hz。模型数据处理采用常规处理流程。
2.2 物理模拟结果分析按照1.3所述的流程,分别开展了不同尺度、不同方向分解结果对比分析。这里只对3层和6层(尺度增加)分解结果、4方向和8方向滤波结果进行对比分析(图 2)。由图 2(a)与图 2(b)的对比可以看出,在相同方向滤波数情况下,6层分解比3层分解效果更好,主要表现在模型右上方4个不同裂缝密度带轮廓和其下方断层展布更加清晰,这可以理解为随着尺度的增加(分解层数增多),高频成分在局部得到体现。这种差异性应该是构造模型中层面构造的局部不平整、断层断距局部不同和构造裂缝带的影响造成的,但是构造裂缝带的具体细节仍然没有显现出来,这可以通过增加高频成分的方向差异性来凸显,即增加方向滤波。由图 2(b)与图 2(c)的对比可以看出,在多尺度分解后,随着方向滤波数目的增加,模型上方设计的简单交叉裂缝带、断裂伴生的裂缝发育带的影像得到增强,并且高频成分的多尺度、多方向滤波可以强化裂缝发育带“竹叶”状分布趋势,符合伴生构造裂缝带的区域分布特征,颜色代表裂缝带发育的强弱。在地震储层预测中,为了描述简洁,通常将预测得到的裂缝带发育强度用“裂缝密度”表示。图 2(d)相当于在只代表裂缝密度的图 2(c)上叠加了裂缝走向,颜色代表裂缝密度,黑色线条代表裂缝方向。图 2(d)展示了如下几个特征:① 基于Contourlet变换的图像增强技术可以清晰地刻画断裂、伴生裂缝带以及非伴生裂缝带发育强弱(裂缝密度);② 随着尺度和方向数的增加,振幅中隐含的裂缝带信息凸显了出来,但是构造层面不平整造成的误差同样得到了放大。因此,该项技术的应用需要做好保幅处理、精细的层位解释等。
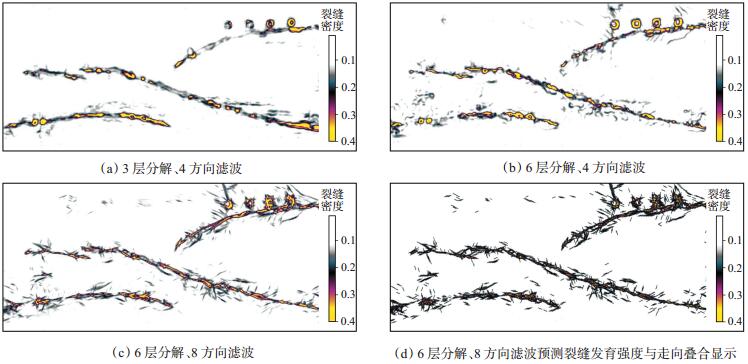
|
下载eps/tif图 图 2 Contourlet变换中不同尺度、不同方向分解结果 Fig. 2 Comparison of results of different scales and different directional decomposition with Contourlet transform |
为了说明基于Contourlet变换的图像增强技术的有效性,将图 2与利用C3算法计算的振幅相干[图 3(a)]和蚂蚁追踪预测结果[图 3(b)]以及基于Curvelet变换的结果[图 3(c)]进行对比与分析。相干计算结果[图 3(a)]与Contourlet变换的小尺度分解结果[图 2(b)]相似,但是在清晰反映大断裂方面不如图 2(b)(特别是模型右上方断裂和左边2条大断裂交界处),优势是在模型上方设计的交叉裂缝带有模糊显示;由相干计算结果[图 3(a)]与Contourlet变换的多尺度、多方向预测结果[图 2(c)]的对比可以看出,无论是在反映大断裂方面还是在反映裂缝带方面,图 2(c)都大大优于图 3(a)。在本次试验中,蚂蚁追踪技术预测结果[图 3(b)]没有很好地刻画出断裂和裂缝的分布特征,预测结果更多的是以条带状突出了断裂和特殊地质体(地层)的不连续性,将地层的小幅度构造刻画成小断裂,这也说明该项技术应用中各种参数的设定对计算结果的影响非常大。Curvelet变换结果[图 3(c)]与图 2(c)相比较,二者都能较好地反映断裂及裂缝带的整体分布特征。Contourlet变换结果[图 2(c)]的最大优势体现在相同参数下,其计算速度要快很多,这和其直接在离散域定义函数息息相关;另外基于Contourlet变换的图像增强技术[图 2(c)]在局部细节分解方面做得更好,这与其不同方向分解时核函数不同相关。
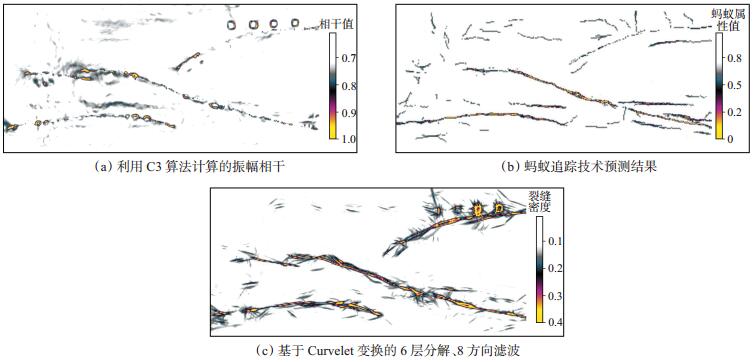
|
下载eps/tif图 图 3 其他3种不同技术的预测结果 Fig. 3 The prediction results of three kinds of techniques |
某油田位于一条控坳断层控制的东断西超箕状盆地,白垩系砂岩油气藏受构造运动影响较大,高角度构造裂缝控制了油气的运移和存储。统计表明,高产井一般位于断裂附近或者构造裂缝带上,精细的断裂构造解释和裂缝带分布预测是该区目的层段实现有效储层预测和井位部署的关键。断裂构造解释的难点在于区内剪切走滑小断层发育,断距较小,利用常规人机交互解释手段很难准确、精细地刻画小断裂的分布。图 4(a)为目的层段特征值相干切片,由于小断裂和裂缝发育,造成低相干背景(黑色模糊区域)出现,同时相干描述的断层平面分布连续性差。图 4(b)为基于Contourlet变换的图像增强技术在工区断裂构造解释中的应用效果。在小尺度、多方向分解情况下,图像增强结果很好地突出了断裂的平面分布特征,清晰地显示了不同断裂的平面组合和分布模式,结合地质规律认识,最终确定了目的层段的断裂分布,为井位部署提供了依据。
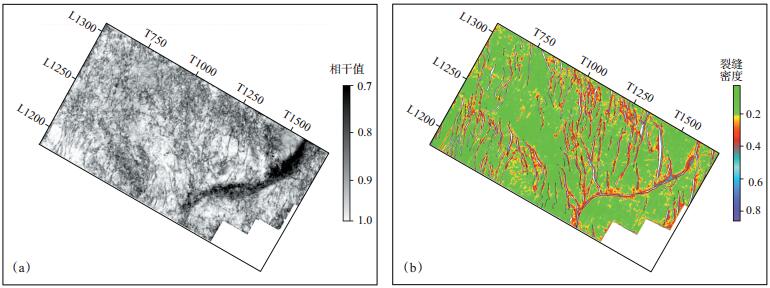
|
下载eps/tif图 图 4 相干切片(a)与基于Contourlet变换的图像增强技术(b)的计算结果 Fig. 4 Calculated results of coherence slice(a)and image enhancement technique based on Contourlet transform(b) |
某油田位于沙河街组三段下部致密泥灰岩储层发育的断陷湖盆,断裂不发育,泥灰岩具有自生自储的特征,岩心和成像测井资料均表明目的层段主要发育高角度的构造裂缝。由图 5(a)可知,尽管工区断裂不发育,但裂缝带仍然集中于断层周围,为构造应力作用下的伴生构造裂缝;湖盆坡折带和洼槽区没有大断裂形成,但裂缝带较发育,这可能是应力释放达到平衡造成的结果,这些裂缝带为目的层致密油气存储创造了有利条件。由图 5(b)可知,工区断裂带受构造影响主要发育北北东—南南西、北东—南西走向裂缝,盆地坡折带和洼槽区主要发育北北西—南南东、近南北走向裂缝。同时看到,裂缝带基本为交叉裂缝形态,呈现网状分布,符合碳酸盐岩储层裂缝分布的特征。
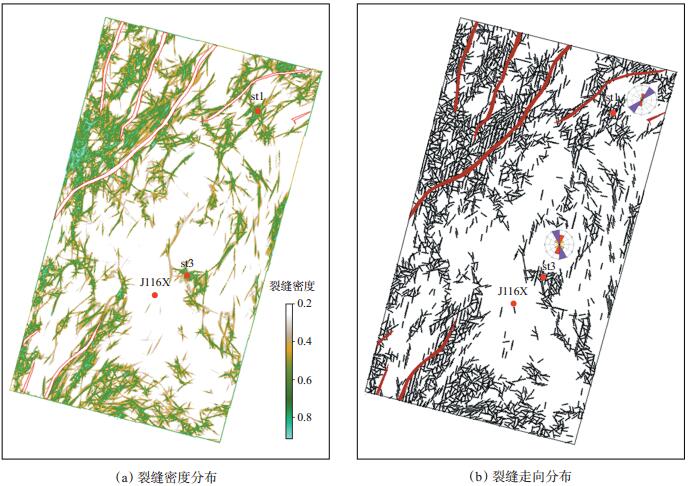
|
下载eps/tif图 图 5 基于Contourlet变换图像增强技术计算的裂缝分布 Fig. 5 Fracture distribution calculated by image enhancement technique based on Contourlet transform |
预测结果得到了高产井st1和J116X井岩心数据验证,并配合其他技术论证了st3井的上钻。st3井在目的层段获得了日产油67m3,扩大了凹陷致密油气藏的勘探范围。st3井钻井资料证实,目的层段主要发育北北西—南南东走向裂缝[图 5(b)],进一步验证了该技术的有效性。
4 结论(1)基于Contourlet变换的图像增强技术通过频率域多尺度分解、多方向滤波,突出数据的尺度性和方向性,与Curvelet变换相比,具有更快的计算速度和更小的冗余度。地震物理模拟正演表明,与主流技术相比,该技术在突出小断裂和构造裂缝带方面具有明显优势。
(2)基于Contourlet变换的图像增强技术已经在多个油田区块的实际生产中得到应用,配合论证与部署了多口高产油气井位,已经实现了相当的经济效益,证明了该方法技术的实用性。
(3)基于Contourlet变换的图像增强技术运算中只有地震叠后数据参与,测井数据只起到验证的作用,因此地震叠后数据的品质对预测结果影响较大。
致谢感谢GeoFrac软件研发组李海山和测试推广组张军舵等技术人员给予的指导!
| [1] |
王时林, 秦启荣, 苏培东, 等.
川北阆中—南部地区大安寨段裂缝预测. 岩性油气藏, 2011, 23(5): 69–73.
WANG S L, QIN Q R, SU P D, et al. 2011. Fracture prediction of Daanzhai member in Langzhong-Nanbu area, northern Sichuan. Lithologic Reservoirs, 2011, 23(5): 69-73. |
| [2] |
邵晓州, 秦启荣, 范晓丽, 等.
川东北黄龙场构造飞仙关组四段底部裂缝预测研究. 岩性油气藏, 2011, 23(5): 96–100.
SHAO X Z, QIN Q R, FAN X L, et al. 2011. Fracture prediction of the bottom of T1f 4 in Huanglongchang structure, northeastern Sichuan Basin. Lithologic Reservoirs, 2011, 23(5): 96-100. |
| [3] |
周文, 尹太举, 张亚春, 等.
蚂蚁追踪技术在裂缝预测中的应用——以青西油田下沟组为例. 岩性油气藏, 2015, 27(6): 111–118.
ZHOU W, YIN T J, ZHANG Y C, et al. 2015. Application of ant trac king technology to fracture prediction:a case study from Xia gou Formation in Qingxi Oilfield. Lithologic Reservoirs, 2015, 27(6): 111-118. |
| [4] |
冯明友, 张帆, 王兴志, 等.
利用IPA技术精细识别裂缝——以柴达木盆地南翼山工区为例. 地球物理学进展, 2010, 25(6): 2054–2060.
FENG M Y, ZHANG F, WANG X Z, et al. 2010. Delineation of frac tures by 3D seismic data IPA technique:a case study in the Nanyishan area, Qaidam Basin. Progress in Geophysics, 2010, 25(6): 2054-2060. |
| [5] |
苟量, 彭真明.
小波多尺度边缘检测及其在裂缝预测中的应用. 石油地球物理勘探, 2005, 40(3): 309–313.
GOU L, PENG Z M. 2005. Multi-scale edge detection of wavelet and application in fracture prediction. Oil Geophysical Prospecting, 2005, 40(3): 309-313. |
| [6] | BONDAR I. 1992. Seismic horizon detection using image processing algorithms. Geophysical Prospecting, 1992, 40(7): 785-800. DOI:10.1111/gpr.1992.40.issue-7 |
| [7] | HESTHAMMER J. 1999. Improving seismic data for detailed struc tural interpretation. The Leading Edge, 1999, 18(2): 226-247. DOI:10.1190/1.1438262 |
| [8] |
陈凤, 李金宗, 李冬冬, 等.
提高地震图像信噪比的非线性各向异性扩散算法模型. 石油勘探与开发, 2004, 31(2): 77–80.
CHEN F, LI J Z, LI D D, et al. 2004. A model of nonlinear anisotro pic diffusion for increasing signal to noise ratio of seismic image. Petroleum Exploration and Development, 2004, 31(2): 77-80. |
| [9] |
孙夕平, 杜世通, 汤磊.
相干增强各向异性扩散滤波技术. 石油地球物理勘探, 2004, 39(6): 651–655.
SUN X P, DU S T, TANG L. 2004. Coherent-enhancing anisotropic diffusion filtering technique. Oil Geophysical Prospecting, 2004, 39(6): 651-655. |
| [10] |
杨宁, 陈婷.
基于多尺度数学形态学地震图象增强方法在裂缝解释中的应用. 信息技术与信息化, 2016, 195(4): 48–51.
YANG N, CHEN T. 2016. Seismic fracture detection based on multi scale morphological seismic image enhancement method. Infor mation Technology and Informatization, 2016, 195(4): 48-51. |
| [11] |
石双虎. 基于新等效介质模型HTI介质中断裂大小、各向异性及频率之间的依赖关系. 长春: 吉林大学, 2007: 83-100.
SHI S H. Dependency relationship of fracture size, anisotropy and frequency in HTI media based on developing equivalent media model. Changchun:Jinlin University, 2007:83-100. |
| [12] | CHAPMAN M. 2003. Frequency-dependent anisotropy due to meso scale fractures in the presence of equant porosity. Geophysical Prospecting, 2003, 51(5): 369-379. DOI:10.1046/j.1365-2478.2003.00384.x |
| [13] | CANDÈS E J, DONOHO D L. Curvelets—a surprisingly effective nonadaptive representation for objects with edges. Nashville: Vaderbilt University Press, 1999: 1-10. |
| [14] |
张广智, 郑静静, 印兴耀.
基于Curvelet变换的多尺度性识别裂缝发育带. 石油地球物理勘探, 2011, 46(5): 757–762.
ZHANG G Z, ZHENG J J, YIN X Y. 2011. Identification technology of fracture zone and its strike based on the Curvelet transform. Oil Geophysical Prospecting, 2011, 46(5): 757-762. |
| [15] |
敬忠良, 肖刚, 李振华.
图像融合——理论与应用. 北京: 高等教育出版社, 2007: 5-6.
JING Z L, XIAO G, LI Z H. Image fusion—theory and applica tions. Beijing: Higher Education Press, 2007: 5-6. |
| [16] | DO M N, VETTERLI M. Contourlet:a directional multiresolution image repersentation. Proc of IEEE International Conference on Image Processing, Rochester, NY, 2002:357-360. |
| [17] |
郑静. 基于Contourlet变换的图像融合算法研究. 青岛: 山东科技大学, 2011: 12-21.
ZHENG J. Study of image fusion based on Contourlet trans form. Qingdao:Shandong University of Science and Technolo gy, 2011:12-21. |
| [18] | DO M N, VETTERLI M. 2005. The contourlet transform:an efficient directional multiresolution image representation. IEEE Transac tions on Image Processing, 2005, 14(12): 2091-2105. DOI:10.1109/TIP.2005.859376 |
| [19] |
易文娟, 郁梅, 蒋刚毅.
Contourlet:一种有效的方向多尺度变换分析方法. 计算机应用研究, 2006, 26(9): 18–22.
YI W J, YU M, JIANG G Y. 2006. Contourlet:efficient directional and multiresolution analytic tool. Application Research of Com puters, 2006, 26(9): 18-22. |
 2017, Vol. 29
2017, Vol. 29



