振幅属性是地震数据处理解释过程中的一个重要参数[1],但是,受上覆地层的影响,从偏移成像剖面中提取的目的层地震波振幅信息,不一定能表征目的层的岩性变化,而可能是上覆地层岩性、构造等要素的反映。
一方面,通过改进地震勘探仪器的性能,地震反射信号的记录精度得到不断提高,为叠前反演和储层预测提供了更高质量的地震资料[2-3]。另一方面,随着勘探领域从构造圈闭到岩性地层圈闭的逐渐延伸,国内外众多学者[4-7]提出了不同的保幅方法来尽可能地保持地震波振幅与目的层界面反射系数之间合理的比例关系,也有学者[8-10]从不同角度评价了这些方法的优劣性。整体而言,这些方法的研究重点大多是如何消除上覆界面的影响以得到真实的反射振幅,但是,受众多因素的制约,现有的保幅方法尚不能做到完全消除上覆界面的影响,业内对上覆界面和目的地层振幅之间的关系仍缺乏研究。
笔者通过实验模拟了地震波在三维倾斜界面速度模型中的传播过程,分析了倾斜界面及其上覆圈闭对目的层地震波振幅的影响,发现受上覆圈闭的影响无法得到目的层岩性的真实反射信息,而目的层的振幅变化同上覆界面之间具有一定的规律性[11]。针对这一现象,本次研究从正演模型出发,利用波动方程进行数值模拟,获取目的层的反射振幅,并通过研究上覆水平界面反射系数与目的层地震波振幅之间的关系,确定目的层地震波振幅随上覆界面反射系数变化而产生的变化规律,以期为利用地震资料正确识别目的层岩性提供理论依据。
1 研究方法通过模型正演,利用双程波动方程模拟目的层地震波振幅的分布,由于双程波动差分方程数值模拟的计算速度较慢,因此采用GPU并行加速来提高差分方程的计算效率。
1.1 高阶交错网格有限差分为了简化模型、方便计算,本次研究使用声波波动方程来模拟地震波传播。相比于单程波,双程波包含的波场信息更丰富,其模拟的地震波场更接近于野外实际观测到的地震波场,因此选取双程声波方程来进行地震波场的数值模拟计算。前人[12-15]针对声波方程交错网格有限差分算法的研究已经相当成熟,在实际地震资料成像处理中已经获得了很好的应用效果。公式(1)为波动方程时间二阶、空间十六阶的三维交错网格有限差分公式,其中,空间维度的阶数越高,计算的精度越高,但相应的计算效率越低。
| $ \left\{ \begin{array}{l} v_{{\rm{x(}}\mathit{i}{\rm{ + 1/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ = }}\mathit{v}_{{\rm{x(}}\mathit{i}{\rm{ + 1/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ - 1/2}}}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta x}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{ + }}\mathit{n}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{ - }}\mathit{n}{\rm{ + 1,}}\mathit{j}{\rm{,}}\mathit{k}}^\mathit{t}} \right]\\ v_{{\rm{y(}}\mathit{i,j}{\rm{ + 1/2,}}\mathit{k}{\rm{)}}}^{t{\rm{ + 1/2}}}{\rm{ = }}\mathit{v}_{{\rm{y(}}\mathit{i,j}{\rm{ + 1/2,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ - 1/2}}}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta y}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{ + }}\mathit{n}{\rm{,}}\mathit{k}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{ - }}\mathit{n}{\rm{ + 1,}}\mathit{k}}^\mathit{t}} \right]\\ v_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j,k}{\rm{ + 1/2)}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ = }}\mathit{v}_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{ + 1/2)}}}^{\mathit{t}{\rm{ - 1/2}}}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta z}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {{\rm{C}}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{ + n}}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{ - }}\mathit{n}{\rm{ + 1}}}^\mathit{t}} \right]\\ p_{{\rm{x(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\mathit{p}_{{\rm{x(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^\mathit{t}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta x}}}}v_{\rm{p}}^2\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{x[}}\mathit{i}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{x[}}\mathit{i}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{{\rm{y(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\mathit{p}_{{\rm{y(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^\mathit{t}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta y}}}}v_{\rm{p}}^2\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{y[}}\mathit{i,j}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{y[}}\mathit{i,j}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\mathit{p}_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^\mathit{t}{\rm{ - }}\frac{{{\rm{\Delta t}}}}{{{\rm{\Delta z}}}}v_{\rm{p}}^2\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{z[}}\mathit{i,j,k}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{z[}}\mathit{i,j,k}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\mathit{p}_{{\rm{x(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} + \mathit{p}_{{\rm{y(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} + \mathit{p}_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} \end{array} \right. $ | (1) |
式中:v(x, y, z)为速度在3个维度上的分量,m/s;v(i, j, k)t为t时刻网格点(i,j,k)处的速度值,m/s;p(x, y, z)为应力在3个维度上的分量,MPa;p(i, j, k)t为t时刻网格点(i,j,k)处的应力值,MPa;vp为声波速度,m/s;Δ t为时间步长,s;Δ x,Δ y,Δ z分别为3个维度上网格步长,m;C为对应的网格参数。式(1)的稳定性条件为
| $ \Delta {\rm{t}} \cdot {V_{\max }} \cdot \sqrt {\frac{1}{{\Delta {{\rm{x}}^2}}} + \frac{1}{{\Delta {{\rm{y}}^2}}}\frac{1}{{\Delta {{\rm{z}}^2}}}} \le \frac{1}{{\sum\limits_{n = 1}^{\rm{N}} {\left| {C\left. {_n} \right|} \right.} }} $ | (2) |
式中:Vmax为速度最大值,m/s;N为空间阶数的一半,此处N=8(空间十六阶)。
在使用波动方程模拟地震记录时,模型的四周会产生边界反射,因此需要人为添加一定厚度的吸收边界来消除边界反射。完美匹配层(PML)吸收边界[16-19]是目前业内应用最广泛且吸收效果比较好的边界条件,具体做法是将衰减系数d引入到式(1)中,得到对应的含PML衰减系数的三维交错网格有限差分公式
| $ \left\{ \begin{array}{l} v_{{\rm{x(}}\mathit{i}{\rm{ + 1/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{x}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{x}}}{\rm{\Delta t}}}}v_{{\rm{x}}(\mathit{i} + 1/2,\mathit{j},\mathit{k})}^{t - 1/2} - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{x}}}\Delta {\rm{t}}}}\frac{1}{{\Delta {\rm{x}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{ + }}\mathit{n}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{ - }}\mathit{n}{\rm{ + 1,}}\mathit{j}{\rm{,}}\mathit{k}}^\mathit{t}} \right]\\ v_{{\rm{y(}}\mathit{i,j}{\rm{ + 1/2,}}\mathit{k}{\rm{)}}}^{t{\rm{ + 1/2}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{y}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{y}}}{\rm{\Delta t}}}}v_{y(\mathit{i,j} + 1/2,k)}^{t - 1/2} - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{y}}}\Delta {\rm{t}}}}\frac{1}{{\Delta {\rm{y}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{ + }}\mathit{n}{\rm{,}}\mathit{k}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{ - }}\mathit{n}{\rm{ + 1,}}\mathit{k}}^\mathit{t}} \right]\\ v_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j,k}{\rm{ + 1/2)}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{z}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{z}}}{\rm{\Delta t}}}}v_{{\rm{z}}(\mathit{i},\mathit{j},\mathit{k} + 1/2)}^{t - 1/2} - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{z}}}\Delta {\rm{t}}}}\frac{1}{{\Delta {\rm{z}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {{\rm{C}}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{ + n}}}^\mathit{t}{\rm{ - }}\mathit{p}_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{ - }}\mathit{n}{\rm{ + 1}}}^\mathit{t}} \right]\\ p_{{\rm{x(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{x}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{x}}}{\rm{\Delta t}}}}p_{{\rm{x}}(\mathit{i},\mathit{j},\mathit{k})}^t - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{x}}}\Delta {\rm{t}}}}\frac{{v_{\rm{p}}^{\rm{2}}}}{{\Delta {\rm{x}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{x[}}\mathit{i}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{x[}}\mathit{i}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{{\rm{y(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{y}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{y}}}{\rm{\Delta t}}}}p_{y(\mathit{i},\mathit{j},\mathit{k})}^t - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{y}}}\Delta {\rm{t}}}}\frac{{v_{\rm{p}}^{\rm{2}}}}{{\Delta {\rm{y}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{y[}}\mathit{i,j}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{y[}}\mathit{i,j}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2,}}\mathit{k}{\rm{]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\frac{{{\rm{2 - }}{\mathit{d}_{\rm{z}}}{\rm{\Delta t}}}}{{{\rm{2 + }}{\mathit{d}_{\rm{z}}}{\rm{\Delta t}}}}p_{{\rm{z}}(\mathit{i},\mathit{j},\mathit{k})}^t - \frac{{2\Delta {\rm{t}}}}{{2 + {d_{\rm{z}}}\Delta {\rm{t}}}}\frac{{v_{\rm{p}}^{\rm{2}}}}{{\Delta {\rm{z}}}}\sum\limits_{\mathit{n}{\rm{ = 1}}}^{\rm{8}} {\mathit{C}_\mathit{n}^{{\rm{(8)}}}} \left[ {\mathit{v}_{{\rm{z[}}\mathit{i,j,k}{\rm{ + (2}}\mathit{n}{\rm{ - 1)/2]}}}^{\mathit{t}{\rm{ + 1/2}}}{\rm{ - }}\mathit{v}_{{\rm{z[}}\mathit{i,j,k}{\rm{ - (2}}\mathit{n}{\rm{ - 1)/2]}}}^{\mathit{t}{\rm{ + 1/2}}}} \right]\\ p_{\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}}^{\mathit{t}{\rm{ + 1}}}{\rm{ = }}\mathit{p}_{{\rm{x(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} + \mathit{p}_{{\rm{y(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} + \mathit{p}_{{\rm{z(}}\mathit{i}{\rm{,}}\mathit{j}{\rm{,}}\mathit{k}{\rm{)}}}^{\mathit{t}{\rm{ + 1}}} \end{array} \right. $ | (3) |
衰减系数d在非边界吸收区域时其值等于0,此时式(3)退化为式(1);在边界吸收区域内,衰减系数d的取值由式(4)计算得到
| $ d = 2{\rm{ \mathsf{ π} AF}}{\left( {\frac{i}{\delta }} \right)^2} $ | (4) |
式中:δ为吸收边界的厚度,m;A为一个常系数;F为子波主频,Hz。
1.2 GPU并行计算GPU的硬件架构中包括较多的计算核心,且其逻辑判断单元较少,这样的架构决定了GPU适合于进行高密集、低复杂度的计算。交错网格有限差分算法中包含大量的重复迭代计算,而且采用式(3)将边界和核心计算区域统一起来可以避免在PML边界位置进行的大量逻辑判断,因此选用GPU并行计算来实现交错网格有限差分算法。
式(3)中每个维度的分量在时间域内计算时都需要前一个时刻的值参与,在空间域内计算时则需要周围点在该时刻的值参与。在进行任务划分时,只能使用串行代码执行时间域内的计算,而将空间域的运算放到GPU上去执行。但是,空间高阶交错网格有限差分方程计算时需要大量的显存读写,对于式(3)中三维十六阶差分方程来说,每计算一个网格点的值都需要读取网格点周围48个网格点的数据,因此需要借助GPU片内高速的共享存储器来降低显存读取冗余度[20-22]。
图 1是对一个三维均匀介质模型分别沿x,y,z等3个方向使用GPU模拟得到的波场快照。该模型为一个正立方体,每个方向的宽度均为1 000 m,激发点被放置在模型正中心点位置。图 1(a)为x=500 m时yz平面的波场快照,图 1(b)为y=500 m时xz平面的波场快照,图 1(c)为z= 500 m时xy平面的波场快照。3个方向的波场快照结果几乎一样,说明GPU计算结果正确可靠,同时,波场快照也揭示出PML边界的吸收效果显著。此外,运行速度上,使用GPU并行计算比传统CPU数值模拟提速大约30倍。

|
下载eps/tif图 图 1 GPU模拟三维均匀介质模型x,y,z等3个方向的波场快照 Fig. 1 Wave field snapshot in three directions of homogeneous medium model calculated by GPU |
三维实验模型基本参数如表 1所列,各参数均满足差分方程稳定性条件[式(4)]。震源使用雷克子波,激发时,炮点放置在地表位置,接收点放置在地下深度为2 580 m处的目的层上。
|
|
下载CSV 表 1 三维实验模型基本参数 Table 1 Parameters of 3D experimental model |
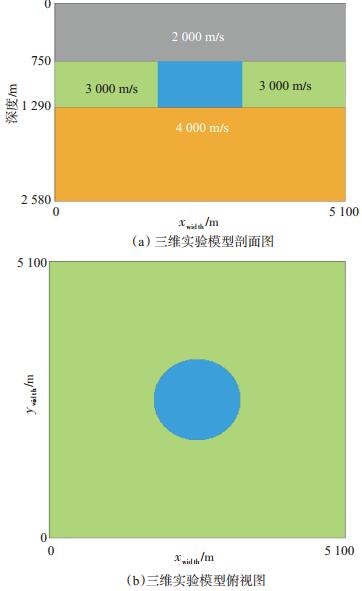
三维实验模型中设计有一速度异常体,该速度异常体为一厚度(540 m)恒定的圆柱体,如图 2所示。实验时,只改变异常体所在蓝色区域的速度V和半径R的大小,不改变异常体厚度及围岩参数,围岩速度设计及俯视效果如图 2(a)、图 2(b)所示。
|
下载eps/tif图 图 2 三维实验模型 Fig. 2 Diagrams of 3D experimental model |
在本模拟实验中,将激发点放置在地表处,接收点放置在地下目的层之上,模拟二分之一自激自收时间的地震波场分布。激发时不选择单炮依次激发,而选择所有激发点同时激发,将全部点震源合并为一个面震源,GPU数值模拟程序会自动保存检波点位置的波场值,随后再提取每个检波点记录长度内的最大振幅值并将其输出,便可得到目的层地震波振幅分布。对于图 2所示的实验模型,地震波从地表传播到目的层的最长时间约为2 550 ms,所以在数值模拟时,应将记录长度设置的比2 550 ms还要长,才能使地震波传播到目的层并被检波点记录。
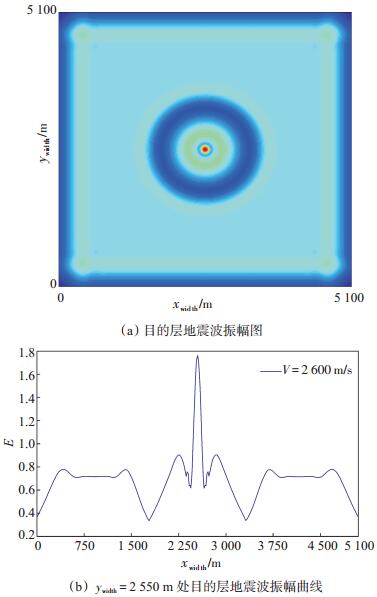
2 上覆水平界面反射系数变化对目的层地震波振幅的影响由于模型中速度异常体位于中心位置,提取的目的层地震波振幅图及振幅曲线都呈中心对称,为了便于分析,只截取中心位置(ywidth=2 550 m)的振幅曲线来进行分析。图 3展示的是当异常体速度V=2 600 m/s、半径R=750 m时,目的层地震波的振幅[图 3(a)]及振幅曲线[图 3(b)]。
|
下载eps/tif图 图 3 目的层地震波振幅记录结果 Fig. 3 Seismic amplitude of the target zone |
将异常体速度V的取值范围设置为2 000~ 4 000 m/s,每隔100 m/s记录一次目的层的振幅结果,振幅曲线汇总情况如图 4所示。所有振幅曲线关于xwidth=2 550 m处的中心点对称,曲线发生剧烈抖动区域的xwidth为1 800~3 300 m,即速度异常体(蓝色区域)所在的区域,各曲线变化最明显之处是其中心峰值的大小。此外,振幅曲线的最小值出现在速度异常区域边界附近位置。

|
下载eps/tif图 图 4 速度V变化时,目的层地震波振幅曲线汇总 Fig. 4 Seismic amplitude curves of the target zone when velocity changes |
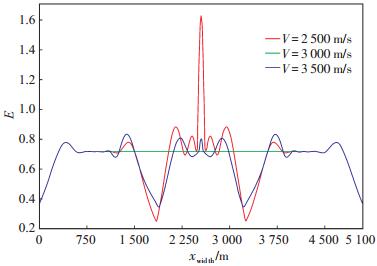
图 5是异常体速度V分别为2 500 m/s、3 000 m/s和3 500 m/s时记录的目的层地震波振幅曲线的对比图,结合图 4可以看出,V= 3 000 m/s是一个分界点,此时模型退化为层状介质模型,目的层的振幅曲线为一条水平线。V= 2 500 m/s时的目的层地震波振幅曲线的峰值明显大于V= 3 500 m/s时的目的层地震波振幅曲线峰值。
|
下载eps/tif图 图 5 目的层地震波振幅曲线对比 Fig. 5 Seismic amplitude curves of the target zone |
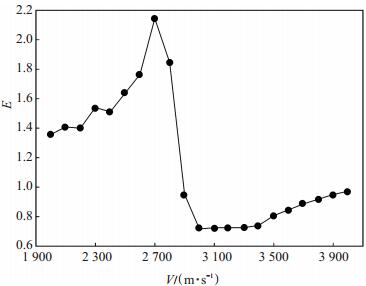
图 6所示的变化曲线是由图 4中所有振幅曲线的峰值(振幅曲线的中心点值)绘制而成的目的层地震波振幅峰值变化曲线,目的层地震波振幅曲线的峰值先随着异常体的速度增大而增大,并在异常体速度V=2 700 m/s时达到最大值,而后陡然变小,且在异常体速度V=3 000 m/s时,峰值最小,之后开始平缓递增。由此推测:上覆异常体的速度在接近围岩速度时,存在一个临界速度,使得目的层地震波振幅曲线的峰值达到最大值。如在本次实验中,当异常体速度在2 700 m/s附近时,目的层地震波振幅曲线的峰值达到最大,本实验目前尚无法确定这个临界速度及其与异常体围岩速度的关系,影响这一临界速度的因素需要做更进一步的实验分析。
|
下载eps/tif图 图 6 目的层地震波振幅曲线峰值变化统计 Fig. 6 Change of amplitude peak values of the target zone |
为了分析速度异常体大小对目的层地震波振幅的影响,将异常体半径R从150 m逐步增大到1 500 m,每隔150 m记录一次目的层地震波振幅,并将异常体速度分别设置为V=2 500 m/s和V=3 500 m/s,进行实验对比。
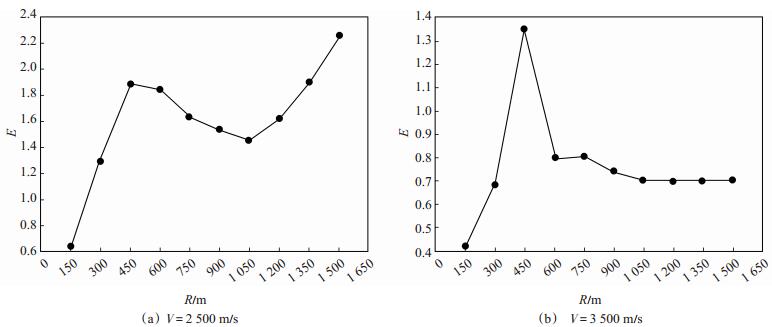
图 7、图 8分别为异常体速度V=2 500 m/s和V=3 500 m/s时,不同半径大小下记录的目的层地震波振幅曲线。从图中可见,振幅曲线最小值所在位置与速度异常体半径R对应。分别统计2种速度情况下,异常体半径R变化时,目的层地震波振幅曲线峰值的变化(图 9),异常体速度V=2 500 m/s时,目的层地震波振幅曲线峰值的变化总体上呈现增大的趋势,但中间有一段慢慢递减再上升的区域,且在R=450 m时,峰值达到最大[图 9(a)];异常体速度V=3 500 m/s时,目的层地震波振幅曲线峰值呈现出先增大再陡降再趋于平稳的变化趋势,且在R=450 m时,峰值达到最大[图 9(b)]。由此推测,上覆速度异常体存在一个可使目的层地震波振幅曲线峰值达到最大的临界半径R,本次实验尚无法确定这一临界半径R及其与异常体厚度之间的关系,这也是下一步实验的努力方向。

|
下载eps/tif图 图 7 异常体速度V=2 500 m/s时,半径R对目的层地震波振幅的影响 Fig. 7 Influence of radius on seismic amplitude with velocity of 2 500 m/s |

|
下载eps/tif图 图 8 异常体速度V=3 500 m/s时,半径R对目的层地震波振幅的影响 Fig. 8 Influence of radius on seismic amplitude with velocity of 3 500 m/s |
|
下载eps/tif图 图 9 目的层地震波振幅曲线峰值随R变化情况统计 Fig. 9 Peak values of seismic amplitude with radius change |
(1)水平界面上覆速度异常体的大小决定了目的层地震波振幅发生抖动的变化范围。
(2)在异常体大小不变的前提下,目的层地震波振幅曲线中心峰值先是随着上覆速度异常体速度的增大而增大,在异常体速度略小于围岩速度时,存在一个临界速度使得目的层地震波振幅曲线峰值达到最大,而后陡然减小,并在异常体速度等于围岩速度时,峰值降至最小,其后再逐渐上升。
(3)在异常体速度不变的前提下,随着异常体半径的不断增大,若异常体速度小于围岩速度,则目的层地震波振幅曲线中心峰值整体呈现增大趋势,但中间存在一段缓慢递减再上升的区域;若异常体速度大于围岩速度,则目的层地震波振幅曲线中心峰值呈现先增大再陡降再趋于平稳的变化趋势。无论异常体速度跟围岩速度的关系如何,总存在一个临界半径能使目的层地震波振幅曲线中心峰值达到最大。
(4)本次实验尚无法确定临界速度和临界半径的具体值及其与围岩速度、异常体厚度等参数的关系。可以肯定的是,在水平界面反射系数趋于一致时,地震波在穿过界面时发生了比较大的变化,造成这一现象的原因,同速度异常体的形态、周围地质体的速度都密切相关,这将是下一步实验研究的重点。
| [1] |
熊翥.
地层岩性油气藏勘探. 岩性油气藏, 2008, 20(4): 1–8.
XIONG Z. 2008. Exploration of stratigraphic-lithologic reservoirs. Lithologic Reservoirs, 2008, 20(4): 1-8. |
| [2] |
桑怀飞, 毕阿欣, 杨世洲.
地震勘探仪器数据传输分析. 物探装备, 2015, 25(6): 372–374.
SANG H F, BI A X, YANG S Z. 2015. Analysis of seismic data transmission. Equipment for Geophysical Prospecting, 2015, 25(6): 372-374. |
| [3] |
王肃静, 卢川, 游庆瑜, 等.
一种低成本无缆地震仪采集站的研制. 地球物理学报, 2015, 58(4): 1425–1433.
WANG S J, LU C, YOU Q Y, et al. 2015. Design of a low cost noncable seismic acquisition station. Chinese Journal of Geophysics, 2015, 58(4): 1425-1433. DOI:10.6038/cjg20150428 |
| [4] |
凌云研究组.
叠前相对保持振幅、频率、相位和波形的地震数据处理与评价研究. 石油地球物理勘探, 2004, 39(5): 543–552.
LING YUN Research Group. 2004. Study of seismic data processing and appreciation based on prestack relative preservation of amplitude, frequency, phase and waveform. Oil Geophysical Prospecting, 2004, 39(5): 543-552. |
| [5] |
刘建红, 孟小红, 程玉坤.
针对叠前反演的去噪技术. 石油勘探与开发, 2007, 34(6): 718–723.
LIU J H, MENG X H, CHENG Y K. 2007. Pre-stack inversion oriented noise attenuation. Petroleum Exploration and Development, 2007, 34(6): 718-723. |
| [6] |
刘东奇, 常旭, 卢孟夏.
目标函数叠前保幅偏移方法与应用. 地球物理学报, 2006, 49(4): 1150–1154.
LIU D Q, CHANG X, LU M X. 2006. Objective function prestack amplitude preserving migration and its application. Chinese Journal of Geophysics, 2006, 49(4): 1150-1154. |
| [7] |
张志军, 周东红, 孙成禹, 等.
基于三维模型数据的地震振幅补偿处理技术的保幅性分析. 物探与化探, 2015, 39(3): 621–626.
ZHANG Z J, ZHOU D H, SUN C Y, et al. 2015. An analysis of the amplitude preservation of seismic amplitude compensation processing technology based on 3D model data. Geophysical and Geochemical Exploration, 2015, 39(3): 621-626. DOI:10.11720/wtyht.2015.3.32 |
| [8] |
李振春, 朱绪峰, 韩文功, 等.
真振幅偏移方法综述. 勘探地球物理进展, 2008, 31(1): 10–15.
LI Z C, ZHU X F, HAN W G, et al. 2008. Review of true-amplitude migration methods. Progress in Exploration Geophysics, 2008, 31(1): 10-15. |
| [9] |
郭树祥.
地震资料保幅处理的讨论. 油气地球物理, 2009, 7(1): 1–7.
GUO S X. 2009. Discussion of preserved amplitude processing of seismic data. Petroleum Geophysics, 2009, 7(1): 1-7. |
| [10] |
王丹, 孙赞东, 王迪, 等.
基于模型数据的不同反褶积方法保幅性分析. 石油地球物理勘探, 2013, 48(3): 359–365.
WANG D, SUN Z D, WANG D, et al. 2013. Analysis of the amplitude preservation of deconvolution methods based on physical model data. Oil Geophysical Prospecting, 2013, 48(3): 359-365. |
| [11] |
邓帅, 刘学伟, 尤佳春, 等.
上覆地层形态对目的层成像振幅的影响. 科学技术与工程, 2016, 16(31): 51–56.
DENG S, LIU X W, YOU J C, et al. 2016. Influence of overlying stratum on amplitude imaging of target interval. Science Technology and Engineering, 2016, 16(31): 51-56. |
| [12] |
陈生昌, 马在田, 吴如山.
波动方程双程地下方向照明分析. 同济大学学报(自然科学版), 2007, 35(5): 681–684.
CHEN S C, MA Z T, WU R S. 2007. Two-way subsurface directional illumination analysis by wave equation. Journal of Tongji University(Natural Science), 2007, 35(5): 681-684. |
| [13] |
陈可洋, 陈树民, 李来林, 等.
地震波动方程方向行波波场分离正演数值模拟与逆时成像. 岩性油气藏, 2014, 26(4): 130–136.
CHEN K Y, CHEN S M, LI L L, et al. 2014. Directional one-way wave field separating numerical simulation of the seismic wave equation and reverse-time migration. Lithologic Reservoirs, 2014, 26(4): 130-136. |
| [14] |
陈可洋.
各向异性弹性介质方向行波波场分离正演数值模拟. 岩性油气藏, 2014, 26(5): 91–96.
CHEN K Y. 2014. Wave field separating numerical simulation of anisotropic elastic medium directional one-way wave. Lithologic Reservoirs, 2014, 26(5): 91-96. |
| [15] |
辛维, 闰子超, 梁文全, 等.
用于弹性波方程数值模拟的有限差分系数确定方法. 地球物理学报, 2015, 58(7): 2486–2495.
XIN W, YAN Z C, LIANG W Q, et al. 2015. Methods to determine the finite difference coefficients for elastic wave equation modeling. Chinese Journal of Geophysics, 2015, 58(7): 2486-2495. DOI:10.6038/cjg20150724 |
| [16] | BERENGER J P. 1994. A perfectly matched layer for absorption of electromagnetic waves. Journal of Computational Physics, 1994, 114: 185-200. DOI:10.1006/jcph.1994.1159 |
| [17] | LI X F. 2011. PML absorbing boundary condition for seismic numerical modeling by convolutional differentiator in fluid-saturated porous media. Journal of Earth Science, 2011, 22(3): 377-385. DOI:10.1007/s12583-011-0190-9 |
| [18] |
丁科.
PML吸收边界条件影响因素分析. 物探与化探, 2012, 36(4): 623–627.
DING K. 2012. An analysis of factors affecting PML absorbing boundary condition. Geophysical and Geochemical Exploration, 2012, 36(4): 623-627. DOI:10.11720/wtyht.2012.4.22 |
| [19] |
陈可洋.
完全匹配层吸收边界条件研究. 石油物探, 2010, 49(5): 472–477.
CHEN K Y. 2010. Study on perfectly matched layer absorbing boundary condition. Geophysical Prospecting for Petroleum, 2010, 49(5): 472-477. |
| [20] | MICHEA D, KOMATITSCH D. 2010. Accelerating a three-dimensional finite-difference wave propagation code using GPU graphics cards. Geophysical Journal International, 2010, 182(1): 389-402. |
| [21] |
龙桂华, 赵宇波, 李小凡, 等.
三维交错网格有限差分地震波模拟的GPU集群实现. 地球物理学进展, 2011, 26(6): 1938–1949.
LONG G H, ZHAO Y B, LI X F, et al. 2011. Accelerating 3D staggeredgrid finite-difference seismic wave modeling on GPU cluster. Progress in Geophysics, 2011, 26(6): 1938-1949. |
| [22] |
刘守伟, 王华忠, 陈生昌, 等.
三维逆时偏移GPU/CPU机群实现方案研究. 地球物理学报, 2013, 56(10): 3487–3496.
LIU S W, WANG H Z, CHEN S C, et al. 2013. Implementation strategy of 3D reverse time migration on GPU/CPU clusters. Chinese Journal of Geophysics, 2013, 56(10): 3487-3496. DOI:10.6038/cjg20131023 |
 2017, Vol. 29
2017, Vol. 29



