自超声波测试技术应用到岩土工程领域以来，该技术已经成功地应用于解决岩体和土体动弹性参数测试、岩体结构分类、参数确定以及岩体质量评价^[1-2]等方面，因而受到了岩土工程界的广泛重视。碳酸盐岩储层是一种非均匀多孔介质，且裂缝发育，导致超声波在岩石中的传播非常复杂，会出现一系列如反射、透射、散射、吸收及畸变等^[3]声学现象。将超声波转换成热能或者其他形式能量的消耗即为波的吸收衰减现象。超声波在岩石内部孔洞、裂缝等界面的反射和散射现象即为波的散射衰减，其中高频部分波长和孔洞尺寸更加接近，很容易被衰减掉，接收到的信号的振幅会明显降低，因此，相应频谱中的高频成分明显减少。反射、绕射波与直达波存在相位上的差异而相互叠加，导致信号发生畸变。由此可见，声波穿过岩石（或岩体）携带出极其丰富的信息^[3]，它是岩石内部结构特征、岩性信息的综合反映。因此，对这些信号进行分析，就能获取到岩石的各种物性信息。如何从声波信号中获取有用信息，是岩石声波信息处理技术的主要研究课题。

目前，从声波时域^[4]信号中可获取的参数有声速（首波波速）、声波衰减系数（首波振幅衰减）及时域最大振幅。从频域^[5]信号中了解声波频率特征，通常可获得的参数有主频率、频域最大振幅及谱面积等。前人已对声波信号进行了大量研究，刘向君等^[6-8]、杨超^[9]主要利用超声波时域信号分析的方法对碳酸盐岩的含水饱和度、孔隙度等因素进行了预测，但却忽视了声波频域信号所携带的大量信息，且并未对碳酸盐岩超声波传播的各向异性特征进行研究；林玫玲等^[10]采用频谱分析处理了裂隙岩样的声波数据，并对岩样裂隙位置和数量进行了定性分析；赵明阶等^[11]将岩石声波信号分解成不同频带通道的小波分量，并分析了各频带信号；周治国等^[12]对3种岩样声波的波谱进行分析后发现，岩心饱和水后纵、横波主频率均明显降低。已有的研究大多都是针对裂缝发育程度较低的致密岩心，均未涉及到孔洞及裂缝发育的碳酸盐岩声波参数的各向异性特征，因此，对碳酸盐岩声学参数的变化特征有必要进行更加深入的研究。以孔洞、裂缝发育程度不同的碳酸盐岩为研究对象，分别通过烘干和饱和水碳酸盐岩声波物理实验和频谱数值分析，对岩石中在不同方向传播的声波波形、声波速度进行分析，并利用傅里叶变换考察声波信号主频率的变化特征，以期为进一步了解碳酸盐岩的声波传播规律提供依据。

实验所用碳酸盐岩岩样取自四川盆地龙王庙组。制样时，按垂直和平行轴向方向切割、打磨并标注岩样的轴向方向，制成60 mm × 60 mm × 60 mm的立方体岩样。岩样每两端面间不平整度误差小于0.3 mm，以确保岩样端面平行，最大偏差小于0.25°。从宏观上观测岩心，可以发现不同岩样孔洞尺寸具有较大差异，其中岩心J-5，J-9，M-1在垂直轴向oo方向还具有明显的层理性裂缝。对岩样水理性质进行了测试，结果如表 1所列。将岩样烘干（置于100~110 ℃烘箱内12 h后自然冷却），在3个方向（相互正交的oo，aa和bb方向）进行纵波测试；之后再将岩样放入有三通开关的真空容器中，注水抽气饱和水（真空饱和水）保持24 h后，对岩样进行纵波测试。

表 1(Table 1)

表 1 岩样水理性质测试结果 Table 1 Test results of water physical properties of rock samples 岩心编号 (oo×aa×bb)/ mm 孔隙度/ % 饱和水率/ % 干燥岩样密度/（g·cm-3） 饱和水岩样密度/（g·cm-3） J-9 59.9 ×59.9×59.8 0.58 0.25 2.77 2.78 J-5 59.9×59.7×60.0 0.83 0.36 2.81 2.82 J-3 59.6×59.8×59.6 1.73 0.33 2.80 2.81 J-4 59.6×59.8×60.0 2.19 0.29 2.80 2.81 S-4 60.2 × 59.2 × 59.3 2.32 0.28 2.78 2.79 S-3 59.9×59.1 ×59.1 2.35 0.36 2.79 2.80 S-1 59.7×59.8×59.8 3.71 0.60 2.73 2.75 S-5 61.8 × 59.5 × 59.6 4.40 0.49 2.82 2.84 L-2 60.1 ×59.9×60.1 5.06 1.11 2.62 2.65 M-2 59.2×59.9×59.1 5.37 0.83 2.68 2.71 J-8 59.8×59.8×60.2 8.38 0.66 2.68 2.69 L-1 60.2 × 59.3 × 59.4 7.21 1.69 2.59 2.63 M-1 59.9×60.0×59.5 8.80 1.81 2.55 2.60 L-3 59.8×59.6×60.0 9.12 2.55 2.52 2.58 J-7 60.0×60.0×59.9 9.15 1.35 2.53 2.56 J-6 59.4×59.8×59.6 9.56 1.47 2.57 2.60

下载CSV 表 1 岩样水理性质测试结果 Table 1 Test results of water physical properties of rock samples

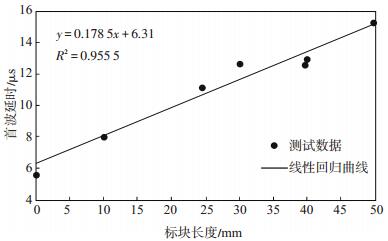
实验使用西南石油大学自行研制的用于岩心筛选的声波测量系统，该系统由声波激发器、超声波探头、岩心夹具、示波器、个人计算机及人机交互软件组成。采用激发频率为50 kHz的探头发射出超声波脉冲，通过Ultra Scope软件采集接收端探头声波波形，采样间隔为2 μs，采样数为600个。该系统能对声波波形进行精确记录，并保证声波波形精确重建。采用不同长度标块线性回归测试该系统的固定延时，测试结果如图 1所示。

图 1

Fig. 1

下载eps/tif图 图 1 声波系统固定延迟时间测试 Fig. 1 Acoustic testing of fixed delay time

测试时，岩样测点固定，处于零应力状态，温度为正常室温（27 ℃）。声波波速可由下式得到：

式中：V为声波波速，cm/s；L为岩心长度，m；t为声波通过岩心的时间，s；t₀为声波系统固定延时。

定义岩心在aa，bb，oo这3个方向的波速或主频率的最大差值与波速或主频率平均值的比值为碳酸盐岩的声波各向异性系数γ，进而评价干燥和饱和水岩心的各向异性特征，γ的计算式为

式中：V_oo, V_aa, V_bb分别为岩心在aa，bb，oo这3个方向的声波波速或主频率。

利用傅里叶变换的方法^[13]对信号进行分解，并按频率展开，使其成为频率的函数，进而在频域中对信号进行研究和处理。任何形状的信号都可以视为无限个不同频率的正弦交变信号的叠加，在数学上用傅里叶序列来表述。假设有一个周期信号x（t），其周期为2 L，傅里叶变换的离散形式^[13]可以表示为

其中

式中：a₀, a_k, b_k为傅里叶系数；N为变换区间长度；m为取样点数，个。

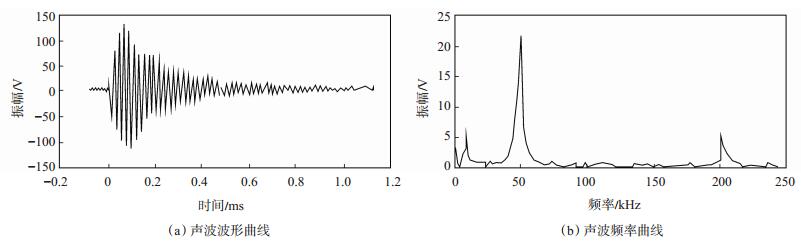
依据式（3）可以将离散的波形时域采样数据转化为频域波形，在频域上对其进行分析。设置采集系统的采样数为600个，采样间隔为2 μs，能够识别波形的最大频率为250 kHz，完全可以分辨出本实验中发射声波的频率。利用上述理论，编制傅里叶变换程序，对采集的声波时域离散信号进行分解，得到信号的频率特征。图 2为探头对接时的时域波形和傅里叶变换后的频域波形。从图 2可以看出，探头对接时域波形呈漏斗状，主频率突出，为50 kHz。

图 2

Fig. 2

下载eps/tif图 图 2 原始波形时域记录及其振幅谱 Fig. 2 Acoustic wave records and its spectrum

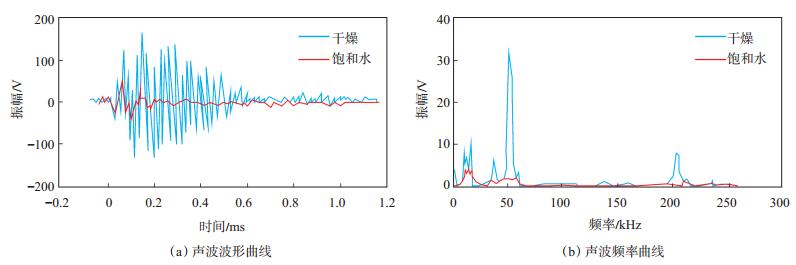
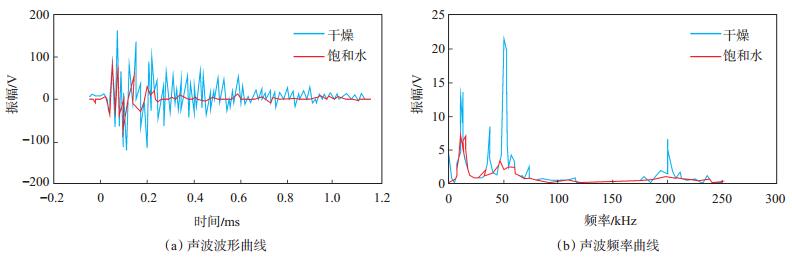
声波信号透射过岩心后的波形差异明显，这是由传播介质对激发信号的滤波作用和介质的吸收作用造成的^[14]。为进一步分析岩样在干燥和饱和水状态下声波波形的变化规律，将接收到的时域信号经傅里叶变换转换为频域信号，并计算出它们的振幅谱，进而从时域和频域2个方面分别考察岩样滤波作用的差异（图 3~5）。

图 3

Fig. 3

下载eps/tif图 图 3 岩样J-6在oo方向干燥和饱和水情况下的声波波形及频率曲线 Fig. 3 Acoustic wave and frequency curves of sample J-6 in the oo direction under desiccated and water-saturated conditions

图 4

Fig. 4

下载eps/tif图 图 4 岩样J-6在aa方向干燥和饱和水情况下的声波波形及频率曲线 Fig. 4 Acoustic wave and frequency curves of sample J-6 in the aa direction under desiccated and water-saturated conditions

图 5

Fig. 5

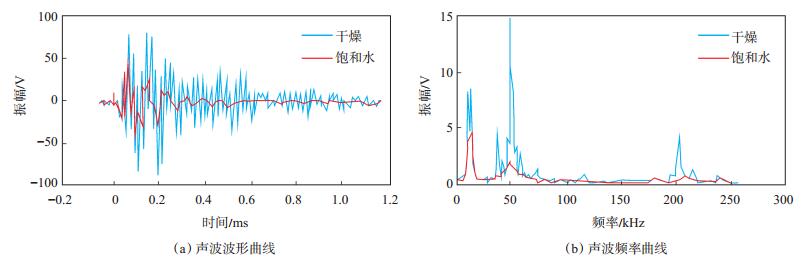
下载eps/tif图 图 5 岩样J-6在bb方向干燥和饱和水情况下的声波波形及频率曲线 Fig. 5 Acoustic wave and frequency curves of sample J-6 in the bb direction under desiccated and water-saturated conditions

从图 5（a）可以看出，与发射波波形（图 2）相比，透射波^[15]的周期明显增大，振幅减小，饱和水后波形周期进一步扩大，但最大振幅位置提前，说明饱和水后岩样内部孔洞被水填充，波的反射、折射叠加作用减弱^[16]。岩样J-6轴向（oo方向）波形较规则，波形包络呈喇叭形，与发射波形大致相同，而aa和bb方向波形发生畸变，由此可判断岩样中裂隙发育^[16]。

从图 5（b）可以看出，在相同的激发信号下，干燥岩样的信号能量集中在50 kHz附近的高频部分，而饱和水岩样的信号能量主要集中在15 kHz以下的低频部分，这一特征反映了饱和水后岩样对声波高频部分的强烈吸收衰减作用。干燥岩样频域不光滑，存在副峰；饱和水后，频域波形主频率突出，高频部分几乎消失。据此可以推断，当岩石中裂隙发育时，会出现频漂现象，声波高频部分衰减程度大，低频部分发育。

按照实验设计方案，分别采集岩心烘干和饱和水后的声波信号，对碳酸盐岩不同环境下的声波波速各向异性特征进行研究。表 2所列为方形碳酸盐岩岩样烘干和饱和水后的波速、各向异性等参数。

表 2(Table 2)

表 2 碳酸盐岩声波波速参数 Table 2 Acoustic wave velocity parameters of carbonate rocks 岩心编号 干燥岩样波速/(km·s-1) γ干燥/ % 饱和水岩样波速/(km·s-1) γ饱和水/ % oo方向 aa方向 bb方向 平均值 oo方向 aa方向 bb方向 平均值 J-9 4.86 5.77 6.28 5.64 25.034 5.99 6.75 6.98 6.57 15.015 J-5 3.22 5.10 5.15 4.49 42.824 4.74 6.08 6.13 5.65 24.699 J-3 5.73 6.09 6.01 5.94 6.170 7.16 7.11 7.23 7.16 1.671 J-4 5.06 4.84 5.34 5.08 9.893 6.59 6.61 6.99 6.73 5.969 S-4 5.39 5.24 5.74 5.46 9.211 6.87 6.46 6.76 6.70 6.154 S-3 4.66 5.35 4.90 4.97 13.806 6.24 6.70 6.62 6.52 7.047 S-1 3.83 4.82 4.36 4.34 22.772 4.95 6.12 5.66 5.58 20.908 S-5 4.92 4.89 4.84 4.88 1.677 6.18 5.88 6.21 6.09 1.429 L-2 3.84 4.30 4.49 4.21 15.382 4.82 5.52 5.43 5.26 13.401 M-2 4.29 4.84 4.71 4.62 11.977 5.74 6.19 5.96 5.96 7.709 J-8 4.14 4.52 4.59 4.41 10.225 5.42 5.79 5.65 5.62 6.668 L-1 3.82 3.81 3.76 3.80 1.640 5.34 5.13 4.96 5.14 7.401 M-1 4.43 5.59 5.50 5.18 22.452 5.65 6.45 6.65 6.25 15.919 L-3 3.62 3.94 3.83 3.80 8.291 4.92 5.22 4.59 4.91 12.788 J-7 4.64 4.85 4.59 4.69 5.531 5.31 5.43 5.32 5.35 2.282 J-6 5.58 5.29 5.61 5.49 5.883 5.58 5.37 5.61 5.52 4.304

下载CSV 表 2 碳酸盐岩声波波速参数 Table 2 Acoustic wave velocity parameters of carbonate rocks

从表 2可以看出，岩样烘干后，纵波平均速度为3.8~5.94 km/s，波速存在各向异性，这表明岩样在3个方向的裂隙发育情况不一致，计算得到的波速各向异性系数为1.677%~42.824%。岩样J-5，J-9和M-1在垂直轴向oo方向层理均较发育，且存在明显的裂缝，其所对应的各向异性系数分别为42.824%，25.034%和22.452%，明显高于其他岩样，这表明岩样的裂缝/层理越发育，则各向异性系数越大；同时，沿oo方向传播的声波波速远低于aa和bb方向，这表明在裂缝或者层理的发育方向上，纵波的传播速度会随着发育程度的增加而降低，据此可以推断出岩样中裂缝/层理的产状。

岩样饱和水后，纵波平均速度为4.91~7.16 km/s，在不同方向上的传播速度均增大；波速各向异性系数为1.43%~24.7%，与干燥岩样相比，饱和水后岩样的波速各向异性系数明显降低，这说明当岩石内部的孔隙和裂缝被地层水填充后，弱化了岩样各向异性特征。

主频率^[16]是指频率域内最大谱峰值的频率值，据此可以定量地考察岩样在干燥和饱和水情况下声波主频率的差异特征。为进一步考察各岩样声波各向异性特征，基于频谱分析原理，对声波信号的主频率进行分析。岩样在干燥和饱和水情况下主频率值如表 3所列。

表 3(Table 3)

表 3 岩样纵波在干燥和饱和水条件下的主频率 Table 3 Dominant frequency of P-wave of rock samples under desiccated and water-saturated conditions 岩心编号 干燥岩样主频率/kHz γ干燥/ % 饱和水岩样主频率/kHz γ饱和水/ % oo方向 aa方向 bb方向 平均值 oo方向 aa方向 bb方向 平均值 J-9 14.19 46.74 50.00 36.98 96.84 11.69 12.52 12.52 12.24 6.78 J-5 9.18 44.02 45.15 32.78 109.72 10.85 12.52 11.69 11.69 14.29 J-3 50.00 13.38 14.17 25.85 141.67 10.02 11.69 11.69 11.13 15.00 J-4 50.00 11.63 11.69 24.44 157.00 10.21 8.35 13.36 10.64 47.09 S-4 14.98 13.31 46.51 24.93 133.16 12.52 10.85 13.36 12.24 20.50 S-3 45.68 49.83 12.54 36.02 103.54 10.02 13.36 10.85 11.41 29.27 S-1 49.25 50.00 48.25 49.17 3.56 10.02 10.02 9.18 9.74 8.62 S-5 13.38 10.83 48.50 24.24 155.43 16.70 11.69 13.36 13.92 36.00 L-2 10.85 9.17 9.17 9.73 17.27 8.35 10.02 10.02 9.46 17.65 M-2 50.00 49.08 14.17 37.75 94.91 10.02 12.52 11.69 11.41 21.91 J-8 46.67 46.67 50.00 47.78 6.97 12.52 11.69 15.03 13.08 25.54 L-1 12.50 8.35 8.31 9.72 43.11 11.69 10.02 10.02 10.58 15.79 M-1 14.98 49.67 46.82 37.16 93.36 10.02 11.69 10.02 10.58 15.79 L-3 10.00 9.17 8.31 9.16 18.45 10.02 10.02 10.02 10.02 0 J-7 49.85 48.41 48.33 48.86 3.11 11.69 14.19 12.52 12.80 19.53 J-6 50.00 49.83 50.00 49.94 0.34 10.84 11.69 12.52 11.68 14.38

下载CSV 表 3 岩样纵波在干燥和饱和水条件下的主频率 Table 3 Dominant frequency of P-wave of rock samples under desiccated and water-saturated conditions

从表 3可看出，干燥岩样的主频率为9.16~49.94 kHz，主频率的各向异性系数为0.34% ~ 157%；饱和水岩样的主频率为9.46~15.03 kHz，主频率的各向异性系数为0~47.09%。岩样在饱和水状态下的纵波主频率明显比干燥情况下要低很多，说明声波主频率对水的影响较为敏感；岩样J-9和J-5在垂直轴向oo方向上裂缝/层理发育，对应轴向主频率明显低于aa方向和bb方向，主频率的各向异性系数偏大，表明主频率的各向异性系数可以作为评价岩心裂缝发育形态及各向异性的指标之一。然而，岩样饱和水后主频率的各向异性系数大大减小，可见在饱和水情况下，主频率的各向异性系数不能很好地评价岩样各向异性值。

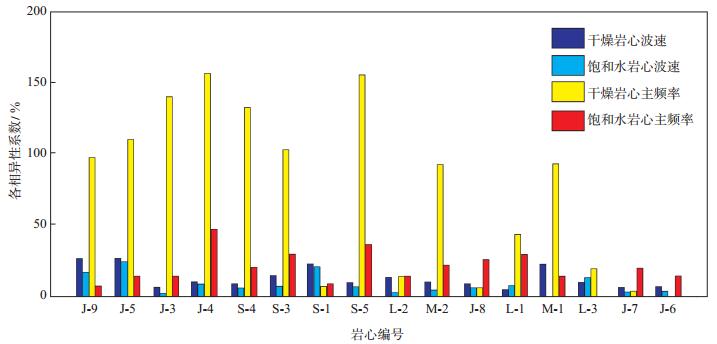
为了更加直观地分析碳酸盐岩在饱和水和干燥情况下声波波速及主频率的各向异性系数的变化情况，将表 2中波速各向异性系数和表 3中主频率的各向异性系数进行了汇总（图 6）。

图 6

Fig. 6

下载eps/tif图 图 6 岩样各向异性系数条形图 Fig. 6 Bar chart of anisotropy coefficient of rock samples

从图 6可以看出，在干燥情况下，声波主频率对岩心的各向异性更加敏感，相比波速，能够更清晰地评价岩样的各向异性特征。在饱和水的情况下，波速和主频率的各向异性系数均较小。

（1）声波透射岩石后，波形发生畸变，周期增大，振幅减小；饱和水后岩样的周期进一步增大，但最大振幅位置提前；干燥岩样频谱图有多峰现象，谱线不光滑，岩样饱和水后频率曲线主频率突出，高频部分衰减程度增大，低频发育。

（2）相比干燥情况，饱和水后岩样的波速增大，而主频率减小，声波信号高频部分能量严重衰减，低频部分能量增加。

（3）岩样的波速和主频率具有明显的各向异性特征，裂缝越发育，波速、主频率的各向异性系数越大，在垂直裂缝方向，纵波速度、主频率明显降低。

（4）干燥岩心的波速和主频率的各向异性系数能够用来很好地评价岩心的各向异性特征，且主频率对岩心各向异性更加敏感；岩心饱和水时，波速和主频率的各向异性系数均大大减小，已不能很好地用来评价岩心各向异性特征。

（5）由于复杂碳酸盐岩储层超声波信号严重衰减和畸变，分辨出有效信息比较困难，未来应该采用小波变换、S变换等时频分析方法，同时提取时间域、频率域的信息，提高储层信息识别精度。