2. 成都理工大学 地球物理学院, 成都 610059
2. College of Geophysics, Chengdu University of Technology, Chengdu 610059, China
AVO属性分析、叠前反演等叠前地震数据的处理和解释流程都是以同相轴水平这一假设为前提的,而实际地震资料经过动、静校正后常存在同相轴扭曲不平现象,导致处理结果产生畸变。Spratt[1]和Swan[2]指出:AVO异常对同相轴扭曲非常敏感,这种畸变引起的异常远大于真实的AVO斜率项。曲寿利[3]总结了产生同相轴扭曲的3个原因:① 动校正引起的速度误差,常规速度分析通常以CMP道集具有双曲线型时距曲线为假设前提,而实际地震数据往往并不满足这一假设;② 动校正方法的局限性,采用整体搬家法(Block move sum normal moveout)动校正会造成动校正拉伸;③ 薄层调谐子波拉伸。针对同相轴扭曲的剩余时差校正方法主要有4种:① 剩余静校正法,如郭树祥[4]提出的分频剩余静校正方法,由于同相轴扭曲是随时间和炮检距的变化而随机变化的,剩余静校正法难以完全拉平同相轴;② 统计法,如曲寿利[3]提出的分层开时窗、逐层统计剩余时差的方法,该方法的缺点是计算量大;③ 精细速度分析法,如Swan[5]和周鹏等[6]提出的基于速度调整的道集拉平方法,该方法的应用前提是时距曲线应为双曲线型,而实际地震资料通常难以满足这一要求;④ 互相关法,如Hinkley等[7]提出的动态道集拉平方法,Gulunay等[8]提出的互相关剩余时差校正方法等,这类方法采用滑动时窗逐点计算校正量,校正后会破坏地震道的波组特征。
动态时间规整(Dynamic time warping,DTW)由Sakoe等[9]提出,是一种基于动态规划的模板匹配算法,具有简单高效和抗噪声能力强等优点,广泛应用于语音信号处理和图像识别等领域。原始DTW算法计算效率并不高,业内学者提出了多种改进算法,如Salvador等[10]提出的快速DTW,AlNaymat等[11]提出的稀疏DTW等。DTW算法存在的最大缺陷是计算过程完全依赖采样点之间的Euclidean距离[12],而没有考虑时间序列波形的相似性。针对这一缺陷,Zhang等[12]提出了基于形状上下文(Shape context,SC)的DTW算法,即SC-DTW算法,该算法利用形状上下文是一种良好的局部形状描述因子,并且对形状畸变具有较好的鲁棒性等特性,极大地改进了DTW算法[13-14]。
本次研究在探讨DTW算法理论的基础上,提出基于SC-DTW算法的叠前道集剩余时差校正方法,以期实现在保持地震波组特征前提下的同相轴拉平处理。
1 方法原理 1.1 DTW算法原理叠前CMP道集中的各道地震序列,因反映的是地下同一点的地质信息而具有相似性,这种相似性可通过Euclidean距离进行定量评价。Euclidean距离对时间轴畸变非常敏感,由于同相轴的畸变,导致2个地震道之间的相似系数往往比较低。因此,在时间轴上对地震道进行拉伸压缩,可以提高地震道间的相似性,实现同相轴拉平的目的。假设模板匹配的2个序列分别为参考序列X = (x1, x2, …, xN)和计算序列Y = (y1, y2, …, yM),则它们的Euclidean距离为
| $ D\left( {X, Y} \right) = \sqrt {\sum\limits_{i = 1}^N {\sum\limits_{j = 1}^M {{{\left( {{x_i} - {y_i}} \right)}^2}} } } $ | (1) |
式中:D为Euclidean距离;xi为序列X的第i个元素;yi为序列Y的第j个元素。
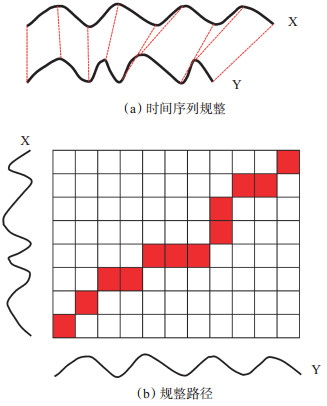
DTW算法是通过动态规划对时间序列进行自适应伸缩,使2个时间序列具有最佳相似性(图 1)。
|
下载eps/tif图 图 1 DTW算法示意图(据文献[15]修改) Fig. 1 Diagram of DTW algorithm |
图 1(a)中上下2条实线分别为参考序列X和待处理序列Y,虚线连接2个序列的相似点,对Y进行伸缩,使2个序列的相似点具有相同的时间坐标[15]。
DTW算法的核心是计算规整路径,即计算序列X和Y中各样点之间的对应关系,具体计算流程分为以下3步:
第1步,计算N×M维Euclidean距离矩阵
| $ D\left( {i, j} \right) = \sqrt {{{\left( {{x_i} - {y_i}} \right)}^2}} $ | (2) |
第2步,计算累积距离矩阵C的满足条件
| $ \left\{ \begin{array}{l} C\left( {1, 1} \right){\rm{ = }}D\left( {1, 1} \right)\\ C\left( {1, j} \right){\rm{ = }}C\left( {1, j - 1} \right) + D\left( {1, j} \right)\\ C\left( {j, 1} \right){\rm{ = }}C\left( {j - 1, 1} \right) + D\left( {j, 1} \right)\\ C\left( {i, j} \right) = D\left( {i - 1, j - 1} \right) + \min \left[{C\left( {i, j-1} \right), C\left( {i-1, j} \right), C\left( {i-1, j - 1} \right)} \right]i \ne 1, j \ne 1 \end{array} \right. $ | (3) |
第3步,通过C,从C(N, M)到C(1, 1) 反向计算规整路径p = (p1, p2, …, pL)(其中pl = (nl, ml) ∈ [1: N]×[1: N],l ∈[1: L]),通过规整路径将计算序列Y映射为与参考序列X长度相等、波形相似的序列,实现对计算道的时差校正。计算的第1个点为C(N, M),第2个点为C(N -1, M),C(N, M -1) 和C(N -1, M -1) 等3个点中累积距离最小的点,以此类推,且反向计算规整路径时还应该同时满足以下3个条件:① 边界条件为p1 = (1, 1) 和pl = (N, M);② 单调条件为n1 ≤ n2 ≤…≤ nL和m1 ≤ m2 ≤…≤ mL;③ 步长条件为pl + 1-pl ∈{(1,0),(0,1),(1,1)},l ∈ [1: L-1]。条件① 要求规整路径分别以C(1, 1) 和C(N, M)为起点和终点,保证了序列X和Y中的每一个坐标都能在规整路径p中出现。此外,由于地震时间序列的前后关系是明确的,因此,条件② 和③ 须要保证规整路径是单调递增的,且经过DTW时差校正后同相轴的先后次序不会被改变。
经过以上步骤计算出的规整路径能够使序列X和Y之间的Euclidean距离最小,校正之后的波形最相似,且序列数值大小未被改变。规整路径中,网格外的2条曲线分别表示序列X和序列Y,网格为累积距离矩阵,红色标注的网格点为规整路径p[13][图 1(b)]。
1.2 SC基本原理地震道本质上是一个时间序列,受采集因素和地质条件的影响,其波形可能发生时间和振幅等2个维度的畸变。传统DTW算法一般假定计算道与参考道之间仅存在时间维度的畸变,而无振幅维度的畸变,但是真实的叠前各道地震信号振幅值往往存在一定变化,并不能完全满足这种假定。
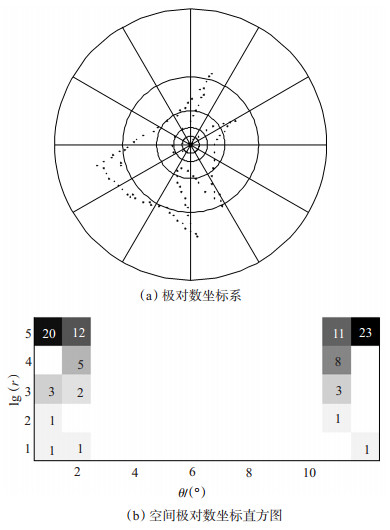
如果将地震道作为振动波形处理,则可以将其看作一种复杂的二维形状,并可以用形状上下文(SC)来表示这种波形。SC的基本思想是用一个采样点集合来表示地震波形状,具体操作是先以参考点为中心建立极对数坐标系,再通过计算周围邻近点与参考点之间的距离和角度信息来描述地震波的局部形状特征(图 2)。图 2(a)揭示了极对数坐标系的建立方式,为了简化算法,一般将方位角θ划分为12个格子,并将径向对数半径划分为5个格子,统计落在参考点周边各个格子中的采样点数量,以此描述局部形状特征。在此基础上,再用1个空间极对数坐标直方图来表征统计出的采样点数量[图 2(b)]。
|
下载eps/tif图 图 2 形状上下文 Fig. 2 Shape context |
Mori等[13]详细描述了SC的计算方法和流程。其基本原理如下:令xic和yic分别代表采样点xi和yi的空间极对数坐标直方图,B为极坐标网格数量,则和的形状代价函数为
| $ {\delta _{{x_i}{y_j}}} = \frac{1}{2}\sum\limits_{b = 1}^B {\frac{{{{\left[{x_i^c\left( b \right)-y_i^c\left( b \right)} \right]}^2}}}{{x_i^c\left( b \right) - x_i^c\left( b \right)}}} $ | (4) |
式中:δxiyj为空间采样点xi和yj的形状代价函数。
显然,局部形状越相似,形状代价函数值越小。
1.3 SC-DTW算法原理规整路径的计算精度取决于测算的相似度,传统DTW算法测算的是2个序列任意样点之间的相似度,局部波形信息往往被忽略,因此,根据相似度计算的可信度必然降低。基于SC的DTW算法(SCDTW)是用形状上下文来取代标准DTW算法中的Euclidean距离,这就能有效避免传统DTW算法容易忽略局部波形的缺点,实现波形的正确匹配。Zhang等[12]以34个UCR(University of california)时间序列数据集为例对SC-DTW算法进行了试算,其中29个数据集的计算结果优于Euclidean距离,这说明SC-DTW算法能够实现时间序列局部形状的正确匹配,所计算出的规整路径精度和可信度高于传统算法。将SC-DTW算法应用于叠前道集的剩余时差校正时,其计算流程如下。
第1步,对序列X和Y中的每一个元素做空间极对数坐标直方图计算,以获取该样点处的图形上下文表示[13]。
第2步,计算序列X和Y中的形状上下文代价矩阵
| $ C_{ij}^{XY} = {\delta _{{x_i}{y_j}}} $ | (5) |
式中:CijXY为形状上下文代价矩阵。
第3步,用形状上下文代价矩阵CijXY代替Euclidean距离矩阵,计算满足公式(3) 的累积距离矩阵C。
第4步,计算满足边界条件、单调条件和步长条件的规整路径。
第5步,利用规整路径对要计算的地震道进行时差校正。
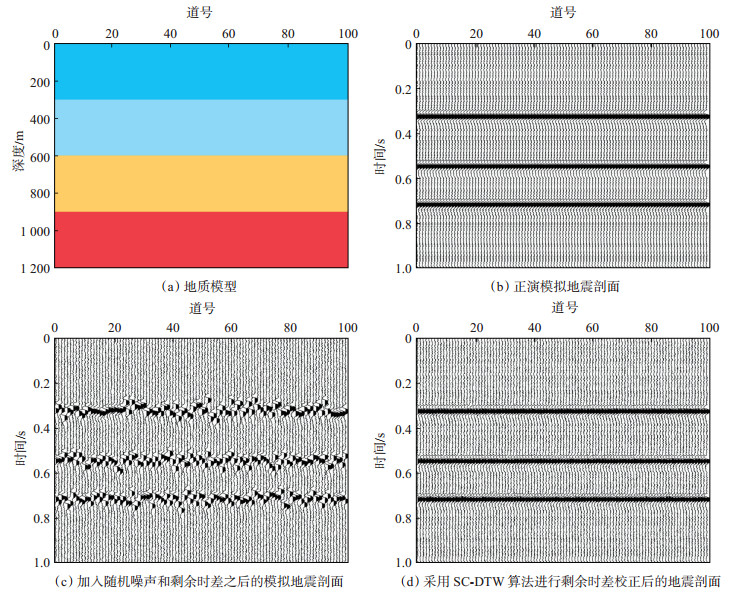
2 数值模拟分析为验证基于SC-DTW的叠前道集剩余时差校正方法的有效性,建立如图 3(a)所示的4层地质模型,地层单层厚度均为300 m,地震波在地层中的传播速度从上到下依次为2 000 m/s,2 300 m/s,2 600 m/s和2900 m/s。图 3(b)是对模型采用20 Hz雷克子波正演模拟出来的理论地震剖面。图 3(c)是加入随机噪声和时差之后的模拟地震剖面,从图中可以看出,地震同相轴发生较大畸变,且连续性变差。图 3(d)是采用SC-DTW算法进行叠前道集剩余时差校正后的地震剖面,与图 3(c)相比,校正后的地震剖面同相轴连续性得到增强,且校正后的波组特征没有发生改变,校正结果[图 3(d)]与理论剖面[图 3(b)]相似度极高。理论模型计算结果表明:基于SC-DTW的剩余时差校正方法对含有噪声的地震信号具有较强的鲁棒性和保幅性,能够有效地压制因剩余时差而引起的同相轴畸变。
|
下载eps/tif图 图 3 基于SC-DTW的叠前道集剩余时差校正方法模型分析 Fig. 3 Modeling analysis by residual moveout correction based on SC-DTW prestack gather |
需要指出的是,参考道的选择非常重要,选择不好会影响动校正拉伸校正效果。本次研究选择角道集角度最小的第1道作为参考道,原因在于角度最小的第1道动校正时差最小、信噪比最高,因此以该道作为基准道,能够取得较好的应用效果。参考道的具体选择方法和依据等可作为下一步的研究内容。
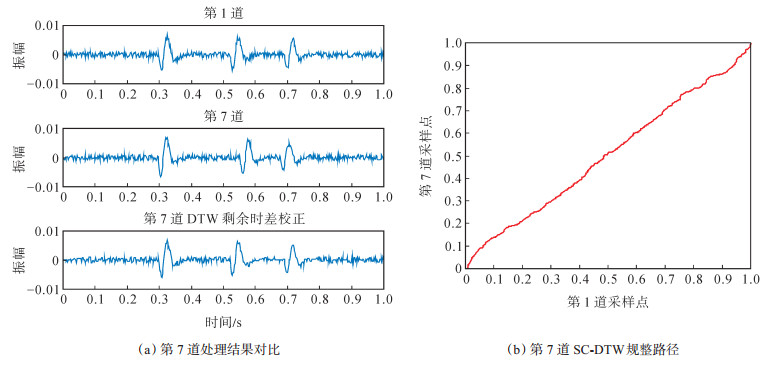
对正演模拟数据的第7道处理结果进行分析(图 4)。以第1道为参考道时,第7道存在剩余时差,经过SC-DTW处理后剩余时差得到校正,且处理前后的波形未发生明显畸变[图 4(a)]。图 4(b)为第7道SC-DTW剩余时差校正的规整路径,纵轴和横轴分别为第7道和第1道的时间坐标,通过规整路径将计算道各时间点波形映射到参考道对应时间点,对原始数据进行时差校正。
|
下载eps/tif图 图 4 第7道SC-DTW处理结果分析 Fig. 4 Analysis of SC-DTW processing results of the 7th trace |
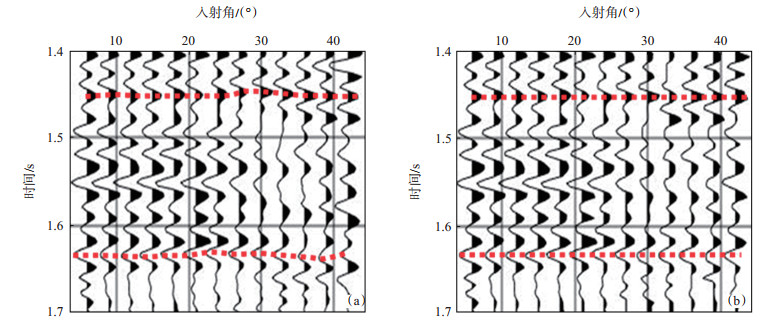
以加拿大东部新斯科舍省海岸的Penobscot工区(数据由OpendTect OSR Team提供)为例,验证基于SC-DTW的叠前道集剩余时差校正方法的实用性。该工区位于Scotian盆地的Sable凹陷内,区内中-晚侏罗世持续沉降,沉积了巨厚的沉积岩。由于下三叠统至上侏罗统广泛发育盐丘,使得该区构造异常复杂,白垩系Mississauga地层和侏罗系Abenaki地层为区内主要储集层。工区采集有三维地震数据88.62 km2( Inline:1 000~1 600,Xline:1 000~1 481),地震信号频带宽度为10~60 Hz,由于数据采集、处理时间较早,导致地震剖面信噪比不高、存在动校正拉伸、叠前道集同相轴不平等现象。图 5(a)为原始地震叠前角道集剖面(Inline 1 536,Xline 1 201),从图中可以看出,地震同相轴连续性差,道集内各道波形变化快,存在不规则的剩余时差,动校正后同相轴扭曲严重[图 5(a)中虚线位置]。图 5(b)为经过SC-DTW算法处理后的道集剖面,从图中可以看出剩余时差及弯曲同相轴得到校正[图 5(b)中虚线位置]。图 6(a)和图 6(b)分别为处理前后角道集的局部放大剖面,从图中可以看出处理前弯曲的同相轴[图 6(a)中虚线位置]得到校正[图 6(b)中虚线位置],处理后的道集满足水平叠加和AVO解释的要求,解释的精度和可信度均得到提高。

|
下载eps/tif图 图 5 Penobscot工区基于SC-DTW的叠前道集剩余时差校正方法校正前a、后b的角道集剖面 Fig. 5 Angle gathers contrast before(a)and after(b)SC-DTW correction of the Penobscot project |
|
下载eps/tif图 图 6 Penobscot工区基于SC-DTW的叠前道集剩余时差校正方法校正前a、后b的角道集局部放大剖面 Fig. 6 Zoom in of angle gathers contrast before(a)and after(b)SC-DTW correction of the Penobscot project |
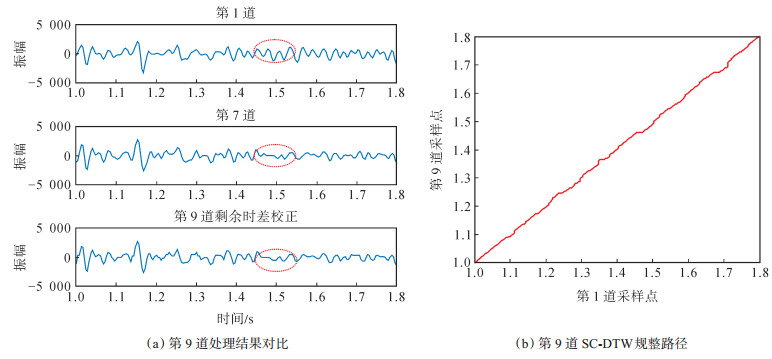
为进一步定性分析该方法在实际地震资料应用中的有效性和实用性,以第1道为参考道,对第9道的处理结果进行分析,图 7(a)是第9道处理前后的波形与参考道的对比,图 7(b)为第9道SC-DTW剩余时差校正的规整路径,通过它对计算道剩余时差进行校正。可以看出参考道1.5s处为波峰,而处理前的第9道对应位置为波谷,二者之间存在时差。经过SC-DTW处理后,时差得到校正,这说明基于SC-DTW的叠前道集剩余时差校正方法能够有效地消除地震道的剩余时差,保持波形特征。
|
下载eps/tif图 图 7 Penobscot 工区叠前角道集Inline 1536,Xline 1201中第 9 道 SC-DTW 处理结果分析 Fig. 7 SC-DTW processing results of the 9th trace of Penobscot projectInline 1536,Xline 1201 |
(1) 基于SC-DTW的叠前道集剩余时差校正方法结合了DTW简单高效和SC对形状畸变具有较强鲁棒性的优点,在地震波场数值模拟和实际生产资料应用中,均取得了明显实效,在剩余时差校正、噪声压制、弯曲同相轴校正等方面效果显著。
(2) SC算子的引入,克服了DTW算法中相似度计算完全依赖采样点之间Euclidean距离这一缺点,实现了以波形相似度测量为基础的地震道波形匹配,处理中能够有效避免2个地震道波峰和波谷之间匹配的错误出现,使DTW算法具有更好的物理意义。
(3) 基于SC-DTW的叠前道集剩余时差校正方法具有良好的抗噪声能力,对地震波形畸变具有较好的鲁棒性,能够较好地消除叠前道集剩余时差,可以提高AVO属性分析、叠前反演等地震资料处理解释的准确性,具有较好的实用性和推广价值。
| [1] |
SPRATT S.
Effect of normal moveout errors on amplitude versus offset-derived shear reflectivity. SEG Technical Program Expanded Abstracts. New Orleans: SEG, 1987.
|
| [2] |
SWAN H W.
1991. Amplitude-versus-offset measurement errors in a finely layered medium. Geophysicists, 1991, 56(1): 41-49.
DOI:10.1190/1.1442956 |
| [3] |
曲寿利.
AVO分析中的剩余时差校正. 石油地球物理勘探, 1991, 26(4): 523–528.
QU S L. 1991. Residual moveout correction in AVO analysis. Oil Geophysical Prospecting, 1991, 26(4): 523-528. |
| [4] |
郭树祥.
分频剩余静校正方法及应用效果分析. 石油地球物理勘探, 2001, 36(6): 735–739.
GUO S X. 2001. Method of frequency-divisional residual statics and its application. OilGeophysical Prospecting, 2001, 36(6): 735-739. |
| [5] |
SWAN H W.
2001. Velocities from amplitude variations with offset. Geophysicists, 2001, 66(6): 1735-1743.
DOI:10.1190/1.1487115 |
| [6] |
周鹏, 刘志斌, 张益明, 等.
动校剩余时差处理方法及应用. 地球物理学进展, 2015, 30(5): 2349–2353.
ZHOU P, LIU Z B, ZHANG Y M, et al. 2015. The processing method and application of the residual moveout NMO. Progress in Geophysics, 2015, 30(5): 2349-2353. DOI:10.6038/pg20150549 |
| [7] |
HINKLEY D, BEAR G W, DAWSON C.
Prestack gather flattening for AVO. SEG Technical Program Expanded Abstracts. Denver: SEG, 2004.
|
| [8] |
GULUNAY N, GAMAR F, HOEBER H.
Robust residual gather flattening. SEG Technical Program Expanded Abstracts. San Antonio: SEG, 2007.
|
| [9] |
SAKOE H, CHIBA S.
1978. Dynamic programming algorithm optimization for spoken word recognition. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1978, 26(1): 43-49.
DOI:10.1109/TASSP.1978.1163055 |
| [10] |
SALVADOR S, CHAN P.
2007. Fast DTW:toward accurate dynamic time warping in linear time and space. Intelligent Data Analysis, 2007, 11(5): 561-580.
|
| [11] |
AL-NAYMAT G, CHAWLAS, TAHERI J.
Sparse DTW:a novel approach to speed up dynamic time warping. The 2009 Australasian Data Mining. Melbourne: Australian Computer Society, 2009.
|
| [12] |
ZHANG Z, TANG P, DUAN R B.
2015. Dynamic time warping under pointwise shape context. Information Sciences, 2015, 315(10): 88-101.
|
| [13] |
MORI G, BELONGIE S, MALIK J.
2005. Efficient shape matching using shape contexts. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2005, 27(11): 1832-1837.
DOI:10.1109/TPAMI.2005.220 |
| [14] |
QIAN D H, CHEN T S, QIAO H.
2016. Background of shape contexts for point matching. Pattern Recognition Letters, 2016, 84: 114-119.
DOI:10.1016/j.patrec.2016.07.016 |
| [15] |
ZINKEA, MAYER D.
Iterative multi scale dynamic time warping. Bonn: Universität Bonn, 2006.
|
 2017, Vol. 29
2017, Vol. 29



