2. 中国石化华北油气分公司 采气一厂, 郑州 450000
2. No. 1 Gas Production Plant, North China Oil and Gas Company, Sinopec, Zhengzhou 450000, China
渭北油田位于鄂尔多斯盆地南部,构造上处于渭北隆起与伊陕斜坡的交汇处,总体上为西北倾向的单斜构造,面积为2 028 km2。研究区目的层段为长3油层组,平均埋深仅550 m,属于浅层油藏。储层岩性以细砂岩为主,平均孔隙度为12.7%,平均渗透率为0.76 mD[1-2]。在沉积作用、成岩作用及构造运动的影响下,研究区储层天然裂缝较为发育,裂缝的存在改善了储层物性,提高了油井的生产能力[3-5]。油井的产量与裂缝发育程度相关,如何定量描述天然裂缝与油井产量的关系,目前国内外尚无好的解决办法。低渗透油藏的开发一般需要进行压裂施工作业,与之对应的产量公式[6-11]有很多,包括考虑启动压力梯度或压裂缝导流能力等,但却没有考虑天然裂缝发育程度的产量公式。笔者基于前人的研究成果,应用分形理论,引入分形维数建立考虑储层天然裂缝的低渗透油藏产量公式,分析天然裂缝发育程度与储层渗透率及压后产能的关系,并对实际生产给出一些建议。
1 裂缝发育程度与分形维数Mandelbrot[12]提出“分形”的术语,将自然界中局部与整体以某种方式相似的形态称为分形,用分形维数的大小来定量描述分形的复杂程度,分形维数用字母D表示。
应用分形理论之前,首先应该判断研究对象的分布是否具有分形特征,如研究储层裂缝时,对岩心采用网格覆盖法来判断储层裂缝是否符合分形特征。具体做法是:用边长为r的正方形网格覆盖岩心剖面,统计包含有裂缝的网格数N(r),改变r的尺度,分别统计其对应的N(r)值,在双对数坐标系中采用最小二乘法对统计数据进行回归分析。研究表明:lgN(r)与lgr之间呈线性关系,因此,储层裂缝的分布具有分形特征[13-16],故可用分形维数D值来定量表征裂缝的发育程度。
一些学者对分形维数与天然裂缝密度之间的关系进行研究后发现,二者满足一定的数量关系[17-18]:
| $ n = f\left( D \right) $ | (1) |
式中:n为天然裂缝密度,cm/cm2;D为分形维数。
一般来说,D值越大,则天然裂缝密度越大,天然裂缝相对越发育。对于岩心,可采用网格覆盖法求取D值,而对于未取心的储层段,通常采用R/S分析法[19-20]将声波时差测井数据作相关运算来求取D值。
2 垂直裂缝井产能预测模型对低渗透油藏油井通常进行压裂而产生压裂裂缝,同时储层中发育有天然裂缝,为此,建立考虑天然裂缝的低渗透油藏垂直裂缝井产能预测模型。模型假设条件为:① 在天然裂缝相对发育区,裂缝相互平行,方向一致,且长度相等;② 上、下均为封闭边界,四周为无限大油层,油层中心有1口垂直裂缝井(图 1),裂缝高度等厚于整个油层,压裂裂缝具有无限导流能力;③ 流体运动符合达西规律;④ 忽略重力和毛管压力的影响;⑤ 等温微可压缩渗流。
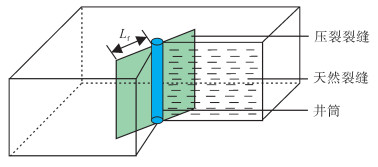
|
下载eps/tif图 图 1 垂直裂缝井物理模型 Fig. 1 Physical model of vertical fractured well |
不考虑启动压力梯度[21-22]和应力敏感[23-24]的影响,根据文献[6],经过单位换算得到无限导流能力垂直裂缝井的产量公式,即
| $ {q_{{\rm{sc}}}} = \frac{{172.8{\rm{\pi }}{{\rm{K}}_{\rm{t}}}h\left( {{p_{\rm{e}}} - {p_{{\rm{wf}}}}} \right)}}{{{\mu _{\rm{o}}}{B_{\rm{o}}}\ln \frac{{2{r_{\rm{e}}}}}{{{L_{\rm{f}}}}}}} $ | (2) |
式中:qsc为油井产量,m3/d;Kt为储层总渗透率,D;h为储层有效厚度,m;pe为原始地层压力,MPa;pwf为井底流压,MPa;μo为地层原油黏度,mPa·s;Bo为地层原油体积系数,无量纲;re为供液半径,m;Lf为压裂裂缝半长,m。
低渗透油藏天然裂缝的发育会提高储层的渗透性,假设流体在裂缝中的流动为平行平板间的流动,则天然裂缝的渗透率[25]可表示为
| $ {K_{\rm{f}}} = 8.33 \times {10^{ - 6}}n{b^3} $ | (3) |
式中:Kf为天然裂缝渗透率,D;b为天然裂缝平均开度,µm。
一般认为双重介质油藏是由基质岩块和裂缝这2种介质组成,且这2种介质均匀分布[25]。当裂缝足够发育,且裂缝之间的连通性很好时,流体流动符合双重介质油藏流体的渗流规律,但对于低渗透油藏,天然裂缝之间的连通性较差,所以不能将发育天然裂缝的低渗透油藏视为双重介质油藏。储层总渗透率不等于基质渗透率与裂缝渗透率的简单叠加,其与天然裂缝的发育程度有关。基于以上认识,结合分形维数,建立考虑天然裂缝的低渗透油藏储层总渗透率计算公式,即
| $ {K_{\rm{t}}} = {K_{\rm{m}}} + \left( {D - 1} \right){K_{\rm{f}}} $ | (4) |
式中:Km为基质渗透率,D。
Kt与D值的大小有关。通常储层裂缝的D值为1~2,当D值为1时,储层天然裂缝不发育,Kt等于Km,为单一介质储层;当D值为2时,Kt为Km与Kf之和,为双重介质储层;当D值在1到2之间时,储层处于单一介质向双重介质的过渡区。
联立式(1)~(4) 可得到考虑天然裂缝的无限导流能力垂直裂缝井的产量计算公式,即
| $ {q_{{\rm{sc}}}} = \frac{{172.8{\rm{\pi }}\left[{{K_{\rm{m}}} + 8.33 \times {{10}^{-6}}\left( {D-1} \right)n{b^3}} \right]h\left( {{p_{\rm{e}}} - {p_{{\rm{wf}}}}} \right)}}{{{\mu _{\rm{o}}}{B_{\rm{o}}}\ln \frac{{2{r_{\rm{e}}}}}{{{L_{\rm{f}}}}}}} $ | (5) |
渭北油田长3油藏的地质及开发参数包括:地层原油黏度为6.64 mPa·s,地层原油体积系数为1.029 5,天然裂缝平均开度为13 µm,油层平均有效厚度为14.42 m,地层平均渗透率为0.76 mD,井距为420 m,井筒半径为0.1 m,生产压差为2.2 MPa,压裂裂缝平均长度为84 m。
选取长3油藏不同深度的岩心来统计天然裂缝的发育情况,并计算裂缝密度值,同时应用R/S分析法计算对应深度的分形维数D值。从裂缝密度与分形维数的关系(图 2)可以看出,长3油藏天然裂缝密度与分形维数之间呈指数关系,其关系式为
| $ n = 0.083{{\rm{e}}^{2D - 1}}, {R^2} = 0.731\;5 $ | (6) |
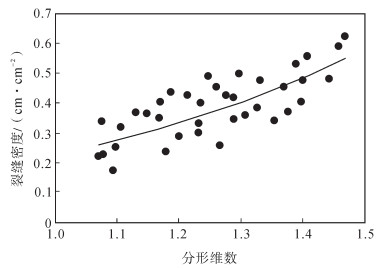
|
下载eps/tif图 图 2 裂缝密度与分形维数的关系 Fig. 2 Relationship between density of fractures and fractal dimension |
式中:R为相关系数。
联立式(5) 和式(6) 可得到渭北油田长3油藏产量计算新公式,即
| $ {q_{{\rm{sc}}}} = \frac{{172.8{\rm{\pi }}\left[{{K_{\rm{m}}} + 6.914 \times {{10}^{-7}}\left( {D-1} \right){{\rm{e}}^{2D-1}}{b^3}} \right]h\left( {{p_{\rm{e}}} - {p_{{\rm{wf}}}}} \right)}}{{{\mu _{\rm{o}}}{B_{\rm{o}}}\ln \frac{{2{r_{\rm{e}}}}}{{{L_{\rm{f}}}}}}} $ | (7) |
与现有的低渗透油藏产量计算公式相比,新公式将天然裂缝的发育程度进行了定量化。在进行产量预测时,可先根据每口井油层的分形维数D值来确定油层的总渗透率,随后进一步预测单井产量。
3.1 模型验证为了验证本文模型的正确性,应用R/S分析法求取渭北油田长3油藏16口油井的分形维数D值,并给出产量计算相关参数(表 1)。
|
|
下载CSV 表 1 渭北油田长3油藏油井参数 Table 1 Oil well parameters of Chang 3 reservoir in Weibei Oilfield |
常规方法对于低渗透油藏天然裂缝发育程度的量化分析具有一定的难度,无法实现单井裂缝发育程度的定量表征,应用式(2) 进行产量预测时,储层总渗透率值Kt很难确定。本文在应用式(2) 计算单井产量时以储层基质渗透率Km代替储层总渗透率Kt,将相关参数代入式(2) 及笔者建立的考虑天然裂缝发育程度的式(7) 分别计算单井产量,并与实际产量进行了对比,结果如表 2所列。
|
|
下载CSV 表 2 不同公式产量计算结果与实际结果对比 Table 2 Comparison of productivity calculated by different formulas and actual productivity |
通过与实际产量相比,当忽视或者不考虑低渗透油藏天然裂缝时,应用式(2) 计算的产量与实际产量相差较大,而通过分形维数量化得到天然裂缝渗透率后,应用式(7) 所计算出的产量与实际产量基本相近,误差较小。由此验证了式(7) 的准确性,同时也说明了天然裂缝对低渗透油藏油井的产能具有较大的贡献,该模型适用于渭北油田天然裂缝发育油藏的产量预测。
3.2 天然裂缝对储层总渗透率的影响渭北油田长3油藏160余口井的分形维数D值分布区间如表 3所列。从表 3可以看出,D值为1.0~1.5,以小于1.3为主。为了研究不同发育程度的天然裂缝对储层总渗透率的影响,基于分形维数数据,根据式(4) 进行计算,得到了储层总渗透率与分形维数的关系曲线(图 3)。
|
|
下载CSV 表 3 渭北油田长3油藏分形维数分布 Table 3 Fractal dimension distribution of Chang 3 reservoir in Weibei Oilfield |
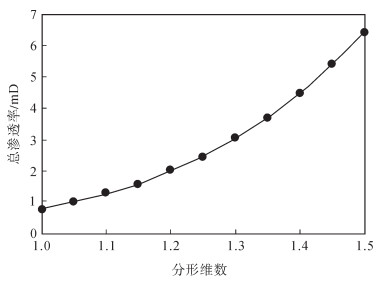
|
下载eps/tif图 图 3 总渗透率与分形维数的关系 Fig. 3 Relationship between total permeability and fractal dimension |
渭北油田长3油藏的基质渗透率Km为0.76 mD,结合总渗透率与分形维数的关系曲线(图 3)可以看出:随着分形维数D值的增加,油藏总渗透率呈指数式增加。D值分别为1.05,1.10,1.15和1.20时,Kt分别为0.98 mD,1.26 mD,1.59 mD和1.99 mD,D值增加至1.3时,储层总渗透率提高至3.02 mD,是基质渗透率的4倍。由此可见,天然裂缝的相对发育可大幅提高低渗透储层的渗透能力,降低流体流动过程中的渗流阻力,进而提高油井产量,有利于低渗透油藏的开发。
3.3 天然裂缝对油井产能的影响当油井不进行压裂时,压裂裂缝半长Lf可取值为2倍的井筒半径,这样式(7) 可转化为平面径向稳定渗流产量公式,即
| $ {q_{{\rm{sc}}}} = \frac{{172.8{\rm{\pi }}\left[{{K_{\rm{m}}} + 6.914 \times {{10}^{-7}}\left( {D-1} \right){{\rm{e}}^{2D-1}}{b^3}} \right]h\left( {{p_{\rm{e}}} - {p_{{\rm{wf}}}}} \right)}}{{{\mu _{\rm{o}}}{B_{\rm{o}}}\ln \frac{{{r_{\rm{e}}}}}{{{L_{\rm{w}}}}}}} $ | (8) |
式中:rw为井筒半径,m。
为了研究天然裂缝对油井压裂后产能的影响,基于式(7)、式(8) 进行计算得到米采油指数随分形维数和压裂裂缝半长变化的关系曲线(图 4)。
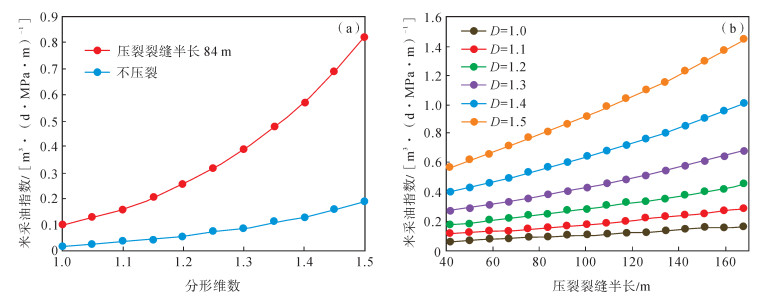
|
下载eps/tif图 图 4 米采油指数与分形维数(a)和压裂裂缝半长(b)的关系 Fig. 4 Relationships of productivity index per-meter with fractal dimension(a)and fracture half length(b) |
从图 4(a)可以看出:对于低渗透油藏,天然裂缝相对不发育(D=1) 时,压裂后米采油指数仅为0.098 m3(/d·MPa·m);随着天然裂缝发育程度的增加,D值分别为1.1,1.2和1.3时的压裂后米采油指数提高至0.16m3(/d·MPa·m),0.26m3(/d·MPa·m)和0.39 m3(/d·MPa·m),分别增加了1.6倍、2.7倍和4倍。从图 4(b)可以看出:当天然裂缝发育程度较低(D≤1.2) 时,随着压裂规模的增大,米采油指数增加幅度较小,压裂增产效果不明显;当天然裂缝发育程度相对较高(D > 1.2) 时,压裂后产能随压裂规模的增大而增大。
当压裂规模相同时,压裂后米采油指数随天然裂缝发育程度的增加近似呈指数式增加;当压裂规模不同时,若天然裂缝相对不发育,则增大压裂规模,压裂后产能的增加不明显,若天然裂缝较为发育,增大压裂规模可较大幅度地提高油井产能。因此,天然裂缝发育程度是影响低渗透油藏压裂后产能最基本的因素。对于低渗透油藏压裂增产作业,应根据不同区域的天然裂缝发育程度针对性地进行压裂规模设计。对于天然裂缝相对较为发育的地区,适当扩大压裂规模,可较大幅度地提高油井产能。同时,压裂时应使用满足储层特征和压裂工艺要求的低伤害压裂液体系,最大限度地减少对天然裂缝的污染。
4 结论(1) 渭北油田浅层油藏发育的天然裂缝连通性差,分布不均匀,这类油藏不是双重介质油藏,储层为单一介质与双重介质之间的过渡储层。
(2) 渭北油田浅层油藏裂缝密度与天然裂缝发育程度相关,可利用分形维数来定量表征裂缝密度。分形维数值越大,则裂缝密度越大,裂缝相对越发育。
(3) 考虑天然裂缝发育程度的低渗透油藏垂直裂缝井产量公式相比于其他学者所建立的公式,考虑了单井的天然裂缝发育程度,计算结果具有较高的准确性,适用于渭北油田浅层油藏的产量预测。
(4) 低渗透油藏产能与天然裂缝的发育程度密切相关,天然裂缝发育程度是影响低渗透油藏压裂后产能最基本的因素。因此,压裂时应考虑天然裂缝发育程度,同时应减少对天然裂缝的污染。
| [1] |
司朝年, 邬兴威, 夏东领, 等.
致密砂岩油"甜点"预测技术研究——以渭北油田延长组长3油层为例. 地球物理学进展, 2015, 30(2): 664–671.
SI C N, WU X W, XIA D L, et al. 2015. The research of"sweet spot" prediction technology for tight sandstone reservoir-a case study of Chang 3 reservoir of Yanchang Formation in Weibei Oilfield. Progress in Geophysics, 2015, 30(2): 664-671. DOI:10.6038/pg20150225 |
| [2] |
吴锦伟, 周思宾, 尹超, 等.
渭北油田长3油藏高产井地质与地震有利模式及应用. 断块油气田, 2016, 23(1): 36–39.
WU J W, ZHOU S B, YIN C, et al. 2016. Geology and geophysical beneficial model of high yielding wells and its application in Chang 3 reservoir, Weibei Oilfield. Fault-Block Oil & Gas Field, 2016, 23(1): 36-39. |
| [3] |
刘格云, 黄臣军, 周新桂, 等.
鄂尔多斯盆地三叠系延长组裂缝发育程度定量评价. 石油勘探与开发, 2015, 42(4): 444–453.
LIU G Y, HUANG C J, ZHOU X G, et al. 2015. Quantitative evaluation of fracture development for Triassic Yanchang Formation, Ordos Basin, NW China. Petroleum Exploration & Development, 2015, 42(4): 444-453. |
| [4] |
曾联波, 漆家福, 王永秀.
低渗透储层构造裂缝的成因类型及其形成地质条件. 石油学报, 2007, 28(4): 52–56.
ZENG L B, QI J F, WANG Y X. 2007. Origin type of tectonic fractures and geological conditions in low-permeability reservoirs. Acta Petrolei Sinica, 2007, 28(4): 52-56. DOI:10.7623/syxb200704010 |
| [5] |
甘秀娥.
低孔低渗砂泥岩储层裂缝发育程度与产能关系. 天然气工业, 2003, 23(5): 41–43.
GAN X E. 2003. Fractures in low porosity and low permeability sand shale reservoirs. Natural Gas Industry, 2003, 23(5): 41-43. |
| [6] |
黄勇, 李春兰, 程林松, 等.
低渗透油藏垂直裂缝井产能评价新方法. 油气地质与采收率, 2010, 17(1): 99–101.
HUANG Y, LI C L, CHENG L S, et al. 2010. A new method of estimating productivity of vertically fracture wells in low permeability oil reservoirs. Petroleum Geology and Recovery Efficiency, 2010, 17(1): 99-101. |
| [7] |
蒋廷学, 单文文, 杨艳丽.
垂直裂缝井稳态产能的计算. 石油勘探与开发, 2001, 28(2): 61–63.
JIANG T X, SHAN W W, YANG Y L. 2001. The calculation of stable production capability of vertically fractured well. Petroleum Exploration & Development, 2001, 28(2): 61-63. |
| [8] |
郝明强, 胡永乐, 李凡华.
微裂缝性特低渗透油藏产能研究. 石油天然气学报(江汉石油学院学报), 2009, 31(2): 100–103.
HAO M Q, HU Y L, LI F H. 2009. Productivity of micro-fractured ultra-low permeability reservoirs. Journal of Oil and Gas Technology(Journal of Jianghan Petroleum Institute), 2009, 31(2): 100-103. |
| [9] |
熊健, 曾山, 王绍平.
低渗透油藏变导流垂直裂缝井产能模型. 岩性油气藏, 2013, 25(6): 122–126.
XIONG J, ZENG S, WANG S P. 2013. A productivity model of vertically fractured well with varying conductivity for low permeability reservoirs. Lithologic Reservoirs, 2013, 25(6): 122-126. |
| [10] |
黄世军, 张晋, 程林松.
低渗透油藏压裂定向井产能计算新公式. 西安石油大学学报(自然科学版), 2015, 30(1): 47–51.
HUANG S J, ZHANG J, CHEN L S. 2015. A new formula for calculating the productivity of fracturing directional wells in low permeability reservoirs. Journal of Xi'an Shiyou University(Natural Science Edition), 2015, 30(1): 47-51. |
| [11] |
尹洪军, 刘宇, 付春权.
低渗透油藏压裂井产能分析. 新疆石油地质, 2005, 26(3): 285–287.
YIN H J, LIU Y, FU C Q. 2005. Productivity analysis of fractured well in low permeability reservoirs. Xinjiang Petroleum Geology, 2005, 26(3): 285-287. |
| [12] |
MANDELBROT B B.
The fractal geometry of nature. San Fran cisco: WH Freeman Publishers, 1982.
|
| [13] |
张庆莲, 侯贵廷, 潘文庆, 等.
构造裂缝的分形研究. 应用基础与工程科学学报, 2011, 19(6): 853–861.
ZHANG Q L, HOU G T, PAN W Q, et al. 2011. Fractal study on structural fracture. Journal of Basic Science and Engineering, 2011, 19(6): 853-861. |
| [14] |
周廷全, 陈俊侠.
济阳坳陷桩西古潜山储层裂缝的分形特征. 中国石油大学学报(自然科学版), 2011, 35(5): 1–5.
ZHOU T Q, CHEN J X. 2011. Fractal characteristics of fracture in zhuangxi buried-hill reservoir, Jiyang depression. Journal of China University of Petroleum(Edition of Natural Sciences), 2011, 35(5): 1-5. |
| [15] |
张吉昌, 田国清, 刘建中.
储层构造裂缝的分形分析. 石油勘探与开发, 1996, 23(4): 65–67.
ZHANG J C, TIAN G Q, LIU J Z. 1996. Fractal analysis on structural fractures of reservoirs. Petroleum Exploration & Development, 1996, 23(4): 65-67. |
| [16] |
尹燕义, 柳成志, 陈洪波, 等.
裂缝型储层裂缝发育程度分形描述方法. 大庆石油学院学报, 1998, 22(1): 10–12.
YIN Y Y, LIU C Z, CHEN H B, et al. 1998. Fractal description of the fracture reservoirs. Journal of Daqing Petroleum Institute, 1998, 22(1): 10-12. |
| [17] |
周英杰, 张敬轩, 杜玉山, 等.
埕北30潜山岩心裂缝的分维数及与裂缝密度的关系. 油气地质与采收率, 2004, 11(3): 19–21.
ZHOU Y J, ZHANG J X, DU Y S, et al. 2004. Fractal dimension of core fractures in Chengbei 30 buried hill reservoir and its relation to fracture density. Petroleum Geology and Recovery Efficiency, 2004, 11(3): 19-21. |
| [18] |
邓攀, 陈孟晋, 杨泳.
分形方法对裂缝性储集层的定量预测研究和评价. 大庆石油地质与开发, 2006, 25(2): 18–20.
DENG P, CHEN M J, YANG Y. 2006. The application of fractal approach to the quantitative estimation research and evaluation of fractured reservoir. Petroleum Geology & Oil Field Development in Daqing, 2006, 25(2): 18-20. |
| [19] |
刘丽丽, 赵中平, 李亮, 等.
变尺度分形技术在裂缝预测和储层评价中的应用. 石油与天然气地质, 2008, 29(1): 31–37.
LIU L L, ZHAO Z P, LI L, et al. 2008. Application of the variable scale fractal technique in fracture prediction and reservoir evaluation. Oil & Gas Geology, 2008, 29(1): 31-37. DOI:10.11743/ogg20080105 |
| [20] |
胡宗全.
R/S分析在储层垂向非均质性和裂缝评价中的应用. 石油实验地质, 2000, 22(4): 382–386.
HU Z Q. 2000. Application of R/S analysis in the evaluation of vertical reservoir heterogeneity and fracture development. Experiment Petroleum Geology, 2000, 22(4): 382-386. DOI:10.11781/sysydz200004382 |
| [21] |
李传亮, 朱苏阳.
再谈启动压力梯度. 岩性油气藏, 2013, 25(4): 1–5.
LI C L, ZHU S Y. 2013. Another discussion on starting pressure gradient. Lithologic Reservoirs, 2013, 25(4): 1-5. |
| [22] |
谢全, 何顺利, 焦春艳, 等.
超低渗单相渗流不存在启动压力梯度的实验. 新疆石油地质, 2011, 32(2): 173–175.
XIE Q, HE S L, JIAO C Y, et al. 2011. Experiment on saturated flow in ultra-low permeability reservoirs without threshold pressure gradient. Xinjiang Petroleum Geology, 2011, 32(2): 173-175. |
| [23] |
焦春艳, 何顺利, 谢全, 等.
超低渗透砂岩储层应力敏感性实验. 石油学报, 2011, 32(3): 489–494.
JIAO C Y, HE S L, XIE Q, et al. 2011. An experimental study on stress-dependent sensitivity of ultra-low permeability sandstone reservoirs. Acta Petrolei Sinica, 2011, 32(3): 489-494. DOI:10.7623/syxb201103018 |
| [24] |
徐新丽.
含微裂缝低渗储层应力敏感性及其对产能影响. 特种油气藏, 2015, 22(1): 127–130.
XU X L. 2015. Stress sensitivity of low-permeability reservoir containing micro-fracture and influence on productivity. Special Oil & Gas Reservoirs, 2015, 22(1): 127-130. |
| [25] |
何更生, 唐海.
油层物理. 2版. 北京: 石油工业出版社, 2011: 63-64.
HE G S, TANG H. Petrophysics. 2nd ed. Beijing: Petroleum Industry Press, 2011: 63-64. |
 2017, Vol. 29
2017, Vol. 29



