油藏数值模拟作为油藏工程分析的主要技术之一,在油藏开采机理研究、开发方案优选等方面正发挥着越来越重要的作用[1]。目前油藏模拟的技术越来越接近油气田开发和生产的实际情况,技术水平得到了显著的提高。油藏数值模拟的计算结果通常用于油田开发决策中,从开发方案的制定到提高油田采收率及部署加密井的整个过程,都离不开油藏数值模拟研究[2]。现阶段油藏数值模拟技术,在碎屑岩油藏的注水开发中已经十分成熟,但难点在于大型数值模型(多网格、多井、长模拟时间)的模拟,主要依赖于计算方法的改进、计算机硬件和并行计算技术的发展[3];对处于多重储层介质(碳酸盐岩)和复杂驱动方式(化学驱)等复杂条件下,油藏数值模拟的研究重点除了计算方法外,更侧重于机理方程的准确建立[4-5]。
油藏数值模拟模型的初始化是任何类型油藏数值模拟研究的首要环节,目前对于油藏数值模型初始化的研究较少。一个高精度的模型初始化过程,是油藏数值模拟获得可靠结果的必要保证[1]。为了体现流体饱和度的不同分布,在以往的实践中,可通过建立多个平衡分区来解决问题[6],但是,相对于油藏模拟中数以万计的网格数量,平衡法所能建立的平衡分区数量是非常有限的。因此,该方法不能很好地体现油藏中流体饱和度的实际变化;也有部分学者[7]考虑了流体饱和度的变化,但在数值模拟初始化时直接导入了三维地质模型的油藏压力和流体饱和度场,之后未作任何处理,导致了其模型在初始条件下就不平衡,即该模型在没有井生产的情况下有流体发生流动,这显然是不符合油藏的实际情况[8]。
枚举平衡法较好的解决了上述矛盾。以最为常见的黑油模型为例,论述了枚举平衡法初始化的主要原理和过程,并结合该方法在中亚哈萨克斯坦某老油田注水开发中的实际应用,以展示其较好的应用效果和较大推广价值。
1 数值模拟初始化过程对比油藏数值模拟以物质平衡方程和达西渗流规律为基本原理,通过数值计算方法,如牛顿-拉夫逊法和预处理共轭梯度法等,求解油藏压力和流体饱和度2类变量[1, 8],油藏数值模拟模型的初始化,就是通过计算获得油藏原始条件下油藏压力和流体饱和度的一个过程,以此为起点,才可以计算随后的油藏压力和流体饱和度。
1.1 数值模拟平衡法初始化过程(1)油藏压力场基于参考点处压力,通过水静力学关系根据深度位置生成:
| $ P = {P_0} + \int_{{h_0}}^h {\rho \;g\;{\rm{d}}\;h} $ | (1) |
式中:P为计算深度处油藏压力,MPa;P0为参考点油藏压力,MPa;h0为参考点的深度,m;h为计算深度,m;ρ为油地下密度,kg/m3;g为重力加速度,m/s2。
(2)流体饱和度场,通过对应的相渗曲线端点值得出,同样以油层段为例,依据油水饱和度的物理意义,有
| $ {S_{\rm{o}}} = 1 - {S_{\rm{w}}} $ | (2) |
| $ {S_{\rm{w}}} = {S_{\rm{wi}}} $ | (3) |
式中:So为含油饱和度,%;Swi为束缚水饱和度,%;Sw为含水饱和度,%。
根据毛管压力定义,利用毛管压力和流体饱和度之间的关系,计算相静压差,反查毛管压力表获得油水过渡带流体饱和度。
1.2 数值模拟枚举平衡法初始化过程(1)油藏压力场的计算过程同平衡法初始化油藏压力场计算过程一致。
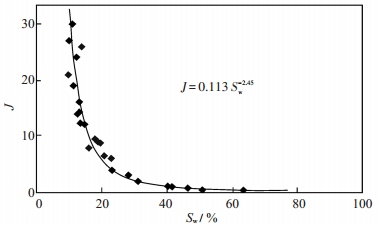
(2)流体饱和度场,则不再根据相渗曲线端点值计算,而是直接启用地质建模输出的各网格块流体饱和度,此过程即为枚举。为了能更真实地反映地层原始的流体饱和度分布,地质建模中可采用J函数来建立流体饱和度场[15] (图 1)。
|
下载eps/tif图 图 1 卡拉姆卡斯油田C区拟合的函数 Fig. 1 Fitting function of C area, Kalamkas oilfield |
| $ J = \frac{{{P_{\rm{c}}}}}{\sigma }{\left( {\frac{K}{\varphi }} \right)^{1/2}} $ | (4) |
式中:J为J函数,无因次;Pc为毛管压力,MPa;φ为储层孔隙度,%;K为储层渗透率,mD;σ为界面张力,N/m。
综合J函数定义和毛管压力表达式,可得C工区含水饱和度为
| $ {S_{\rm{w}}} = 4.27{\left( {\frac{1}{H}\sqrt {\frac{\varphi }{K}} } \right)^{1/2.45}} $ | (5) |
式中:Sw为含水饱和度,%;H为油柱高度,m;φ为储层孔隙度,%;K为储层渗透率,mD。
(3)平衡处理。一般纯油层段初始不含可动水,油层段各个网格块的相渗曲线端点须做相应处理,应用地质建模输出的含水饱和度加以替换。目前相渗曲线端点标定的一般处理方法,是通过坐标轴水平方向线性平移完成,其相渗值不变,重新生成每一个网格新的相渗曲线[5, 9](图 2)。相渗曲线端点标定的公式为
| $ {K_{{\rm{rw}}}}({S_{\rm{w}}}^\prime ) = {K_{{\rm{rw}}}}\left[ {{S_{{\rm{wi}}}} + ({S_{\rm{w}}}^\prime - {S_{{\rm{wi}}}}^\prime )\frac{{1 - {S_{{\rm{or}}}} - {S_{{\rm{wi}}}}}}{{1 - {S_{{\rm{or}}}} - {S_{{\rm{wi}}}}^\prime }}} \right] $ | (6) |
| $ {K_{{\rm{ro}}}}({S_{\rm{w}}}^\prime ) = {K_{{\rm{ro}}}}\left[ {{S_{{\rm{wi}}}} + ({S_{\rm{w}}}^\prime - {S_{{\rm{wi}}}}^\prime )\frac{{1 - {S_{{\rm{or}}}} - {S_{{\rm{wi}}}}}}{{1 - {S_{{\rm{or}}}} - {S_{{\rm{wi}}}}^\prime }}} \right] $ | (7) |

|
下载eps/tif图 图 2 相渗曲线端点标定示意图 Fig. 2 Plot of end point scaling for the relative permeability curves |
式中:Krw为水相相对渗透率,无因次;Kro为油相相对渗透率,无因次;Sw'为标定后的含水饱和度,%;Swi,Swi'分别为束缚水饱和度和标定后的束缚水饱和度,%;Sor为残余油饱和度,%。
完成相渗曲线端点标定后,还需要对毛管压力进行标定,以保证模型初始条件下垂向上的平衡。具体过程为:首先由垂向平衡关系(垂向上流体压力、重力和毛管压力等的平衡),计算出毛管力Pc;然后根据计算出的毛管压力和查毛管压力表的毛管力值Pc'(对应该网格块饱和度的毛管压力值)的比值,来标定毛管压力表中的最大毛管压力Pc max,标定后的最大毛管压力为
中亚哈萨克斯坦卡拉姆卡斯油田C区侏罗系构造是一个东西向的长轴背斜,构造高部位地层遭受到剥蚀,沉积环境以浅海—三角洲相为主。岩性以粉砂岩、细砂岩为主,泥质含量高。物性为中高孔、中高渗透型,平均孔隙度为28.6%,平均渗透率为393 mD。该油田当前处于开发中后期,综合含水为87.4%,采出程度为18.2%。
2.2 初始化效果基于开发调整方案编制的需要,对哈萨克斯坦卡拉姆卡斯油田C区开展了油藏数值模拟研究。数值模拟模型运行前,首先对模型初始化,在此以初始化生成的含油饱和度场为例说明初步检验模型的效果。
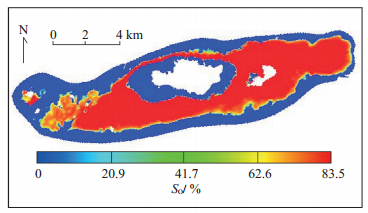
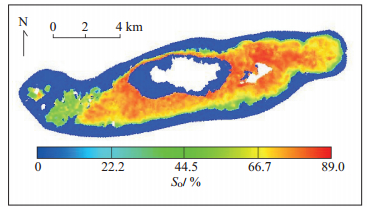
对比发现:常规的平衡法生成的初始含油饱和度场,油层横向上呈现大片的常数区域,红色区的含油饱和度值均为端点值83.5%(图 3),而通过枚举平衡法得到的初始饱和度场,油层横向上不同点的含油饱和度则不再是定值,而是随着空间位置的不同而变化(图 4)。显然,枚举平衡法得到的含油饱和度场更贴近油藏初始流体的真实分布。
|
下载eps/tif图 图 3 卡拉姆卡斯油田C区平衡法初始化原始含油饱和度场 Fig. 3 Initial oil saturation by equilibrium method in C area, Kalamkas oilfield |
|
下载eps/tif图 图 4 卡拉姆卡斯油田C区枚举平衡法初始化原始含油饱和度场 Fig. 4 Initial oil saturation by enumeration-equilibrium method in C area, Kalamkas oilfield |
历史拟合是校核油藏数值模型的核心手段,这里仅以储量拟合和含水拟合为例加以说明。
2.3.1 储量拟合基于枚举过程本身的特点,采用枚举平衡法建立的数值模拟模型拟合储量,地质模型和模型储量之间的误差通常非常小,一般仅仅出现在体积系数和两相流体过渡带,所以一般能实现全区储量的无缝拟合,无须手工再次干预。在本研究案例中,全区储量拟合在未经任何人工调整的情况下,误差仅为2.6%;通过平衡法建立数模模型来拟合储量,地质模型和模型储量的差达6.2%,还须要微调孔隙度,储层厚度,油水界面位置等,才能完成全区储量拟合。
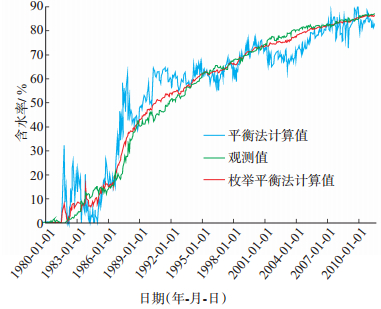
2.3.2 全区单井含水拟合在全区含水拟合中,拟合图 5是模型调试通过后作的第一次计算结果,未经过人工修正。常规平衡法计算值(蓝线)与观测值(绿线),有较大偏离,须要进行宏观调整;枚举平衡法(红线)与观测值趋势已非常接近,几乎无需调整就可直接进入后续流程。
|
下载eps/tif图 图 5 卡拉姆卡斯油田C区全部单井含水拟合曲线 Fig. 5 Water cut fitting curves of C area, Kalamkas oilfield |
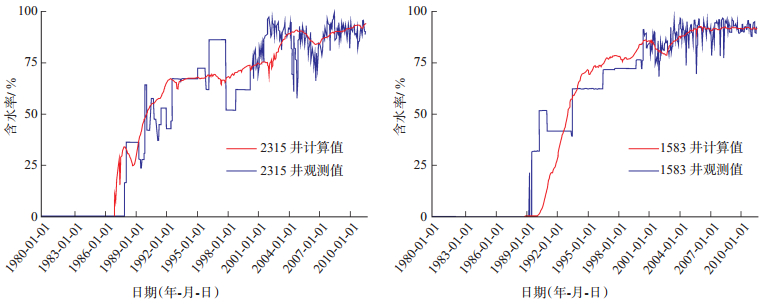
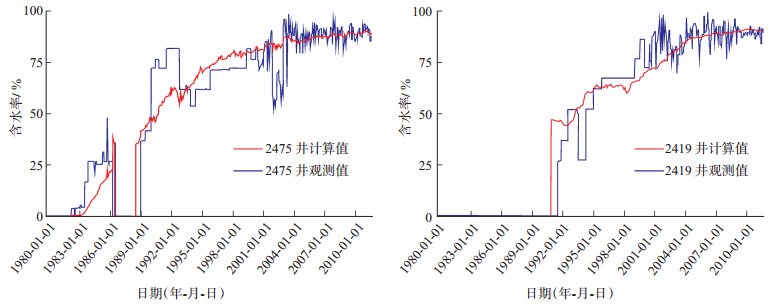
单井含水拟合中,图 6~7是模型调试通过后作的第一次计算结果,这几口井未经过人工修正就基本达到了单井含水拟合的精度要求。经过统计,常规平衡法,能达到拟合要求的井仅20余口,而新方法达到含水拟合要求的井有60多口,约占油井总数的30%,是常规平衡法的3倍。
|
下载eps/tif图 图 6 卡拉姆卡斯油田C区部分单井含水拟合曲线 Fig. 6 Water cut fitting curves of single well in C area, Kalamkas oilfield |
|
下载eps/tif图 图 7 卡拉姆卡斯油田C区部分单井含水拟合曲线 Fig. 7 Water cut fitting curves for parts wells in C area, Kalamkas oilfield |
(1)为了得到比较可靠的初始流体饱和度,枚举平衡法是从提高油藏数值模拟模型初始化精度出发,启用三维地质模型的流体饱和度,在地质建模阶段采用J函数进行处理;通过毛管力标定解决初始化后流体饱和度场的平衡问题;基于物理意义,对测井解释的流体饱和度和相渗曲线端点饱和度作了关联,通过相渗曲线线性平移,生成各个网格块新的相渗曲线。
(2)枚举平衡法建立的数模模型,不仅能使初始流体分布更符合油藏的真实状况,而且能减轻历史拟合的工作量,表现在储量拟合可以自动完成;单井含水的一次性拟合率也明显高于平衡法。
(3)鉴于相渗曲线计算的异常复杂性,难以很精确的生成新的相渗曲线。未来相渗曲线理论计算的新成果,将能进一步完善枚举平衡法油藏数值模拟初始化方法。
| [1] |
韩大匡. 油藏数值模拟基础. 北京: 石油工业出版社, 1993. HAN D K. The fundamental of reservoir numerical simulation. Beijing: Petroleum Industry Press, 1993. |
| [2] |
张烈辉. 油气藏数值模拟基本原理. 北京: 石油工业出版社, 2005. ZHANG L H. The fundamental theory of oil & gas reservoir numerical simulation. Beijing: Petroleum Industry Press, 2005. |
| [3] |
熊玉庆, 曹建文, 张祥. OilCL:一个面向油藏数值模拟并行计算的通信库. 计算机学报, 2000, 23(7): 744-748. XIONG Y Q, CAO J W, ZHANG X. OilCL:A communication library for oil reservoir numerical simulation parallel computing. Chinese Journal of Computers, 2000, 23(7): 744-748. |
| [4] |
李玉梅, 陈开远, 赵玉欣. 提高油藏数值模拟精度的对策研究. 石油天然气学报, 2010, 32(3): 350-352. LI Y M, CHEN K Y, ZHAO Y X. Countermeasures for improving the accuracy of reservoir numerical simulation. Journal of Oil and Gas Technology, 2010, 32(3): 350-352. |
| [5] |
朱焱, 谢进庄, 杨为华, 等. 提高油藏数值模拟历史拟合精度的方法. 石油勘探与开发, 2008, 35(2): 225-229. ZHU Y, XIE J Z, YANG W H, et al. Method for improving history matching precision of reservoir numerical simulation. Petroleum Exploration and Development, 2008, 35(2): 225-229. |
| [6] |
刘玉山, 杨耀忠. 油气藏数值模拟核心技术进展. 油气地质与采收率, 2002, 9(5): 31-33. LIU Y S, YANG Y Z. Key headway of numerical simulation technology for oil-gas reservoir. Petroleum Geology and Recovery Efficiency, 2002, 9(5): 31-33. |
| [7] |
周贤文, 汤达帧, 张春书. 精细油藏数值模拟研究现状及发展趋势. 特种油气藏, 2008, 15(4): 1-6. ZHOU X W, TANG D Z, ZHANG C S. Present situation and growing tendency of detailed reservoir simulation technique. Special Oil and Gas Reservoirs, 2008, 15(4): 1-6. |
| [8] |
李福垲. 黑油和组分模型的应用. 北京: 科学出版社, 1996. LI F K. Application of the black oil model and the compositional model. Beijing: Science Press, 1996. |
| [9] |
张枫, 王振升, 程岩, 等. 油藏数值模拟中油水相对渗透率曲线处理方法. 天然气地球科学, 2010, 21(5): 859-861. ZHANG F, WANG Z S, CHENG Y, et al. Processing methods for relative-permeability curves in reservoir numerical simulation. Natural Gas Geoscience, 2010, 21(5): 859-861. |
| [10] |
于天忠. 水平井化学驱物理模拟及数值模拟研究. 岩性油气藏, 2013, 25(5): 104-108. YU T Z. Research on physical simulation and numerical simulation of horizontal well chemical flooding. Lithologic Reservoirs, 2013, 25(5): 104-108. |
| [11] |
于荣泽, 王楷军, 卞亚南, 等. 特低渗透油藏变渗透率场油藏数值模拟研究. 西南石油大学学报(自然科学版), 2011, 33(5): 98-103. YU R Z, WANG K J, BIAN Y N, et al. Numerical simulation of ultra-low permeability reservoir on variable permeability field. Journal of Southwest Petroleum University(Science & Technology Edition), 2011, 33(5): 98-103. |
| [12] |
刘刚, 李治平, 冯彬, 等. 基于预处理GMRES算法的油藏数值模拟研究. 天然气与石油, 2011, 29(5): 44-46. LIU G, LI Z P, FENG B, et al. Research on numerical reservoir simulation based on preprocessing GMRES algorithm. Natural Gas and Oil, 2011, 29(5): 44-46. |
| [13] |
陈兆芳, 张建荣, 陈月明, 等. 油藏数值模拟自动历史拟合方法研究及应用. 石油勘探与开发, 2003, 30(4): 82-84. CHEN Z F, ZHANG J R, CHEN Y M, et al. Automatic historical matching method and its application in reservoir simulation. Petroleum Exploration and Development, 2003, 30(4): 82-84. |
| [14] |
石广仁, 马进山, 常军华. 三维三相达西流法及其在库车坳陷的应用. 石油与天然气地质, 2010, 31(4): 403-409. SHI G R, MA J S, CHANG J H. 3-D 3-phase Darcy flow method and its application to the Kuqa Depression. Oil & Gas Geology, 2010, 31(4): 403-409. DOI:10.11743/ogg20100402 |
| [15] |
童凯军, 单钰铭, 王道串, 等. 基于毛管压力曲线的储层渗透率估算模型——以塔里木盆地上泥盆统某砂岩组为例. 石油与天然气地质, 2008, 29(6): 812-818. TONG K J, SHAN Y M, WANG D C, et al. CP-curve-based model for estimating reservoir permeability:an example from a sandstone of the Upper Devonian in Tarim Basin. Oil & Gas Geology, 2008, 29(6): 812-818. DOI:10.11743/ogg20080617 |
| [16] |
胡勇, 于兴河, 陈恭洋, 等. 平均毛管压力函数分类及其在流体饱和度计算中的应用. 石油勘探与开发, 2012, 39(6): 733-738. HU Y, YU X H, CHEN G Y, et al. Classification of the average capillary pressure function and its application in calculating fluid saturation. Petroleum Exploration and Development, 2012, 39(6): 733-738. |
| [17] |
马东, 吴华, 曾鸣. 从电阻率数据中得到相对渗透率的新方法. 石油与天然气地质, 2015, 36(4): 695-700. MA D, WU H, ZENG M. A new method for estimating relative permeability with resistivity data. Oil & Gas Geology, 2015, 36(4): 695-700. DOI:10.11743/ogg20150421 |
| [18] |
刘丹, 潘保芝, 陈刚, 等. 致密砂岩气水相渗曲线的统一描述方法. 地球物理学进展, 2015, 30(1): 300-303. LIU D, PAN B Z, CHEN G, et al. Unified description on compact sandstone gas-water relative permeability curve. Progress in Geophysics, 2015, 30(1): 300-303. DOI:10.6038/pg20150143 |
| [19] |
桑丹, 姚约东, 周练武, 等. 利用压汞资料计算复杂断块油藏油水相对渗透率曲线. 断块油气田, 2015, 22(5): 606-609. SANG D, YAO Y D, ZHOU L W, et al. Determination of oilwater relative permeability curves by using mercury injection data for complex fault block reservoir. Fault-Block Oil & Gas Field, 2015, 22(5): 606-609. |
| [20] |
周志军, 薛江龙, 赵立斌. 数值模拟拟合精度方法研究. 岩性油气藏, 2016, 28(1): 101-105. ZHOU Z J, XUE J L, ZHAO L B. Numerical simulation fitting technology:a case study from Longhupao Oilfield. Lithologic Reservoirs, 2016, 28(1): 101-105. |
| [21] |
马勇新, 雷宵, 张乔良, 等. 低渗透油藏有效渗透率计算新模型——以珠江口盆地海相低渗透砂岩为例. 岩性油气藏, 2016, 28(1): 117-122. MA Y X, LEI X, ZHANG Q L, et al. A new model for calculating effective permeability in low permeability reservoir:a case study of low permeability marine sediments reservoir in the Pearl River Mouth Basin. Lithologic Reservoirs, 2016, 28(1): 117-122. |
| [22] |
陈杰, 杜洋, 彭湃, 等. 非稳态油藏理论及其在伊朗A油田的应用. 岩性油气藏, 2015, 27(6): 125-131. CHEN J, DU Y, PENG P, et al. Theory of unsteady reservoir and its application in A oilfield of Iran. Lithologic Reservoirs, 2015, 27(6): 125-131. |
| [23] |
司马立强, 李清, 杨毅, 等. 用J函数法求取碳酸盐岩储层饱和度方法探讨. 岩性油气藏, 2014, 26(6): 106-110. SIMA L Q, LI Q, YANG Y, et al. Using J-function method to calculate saturation of carbonate reservoirs. Lithologic Reservoirs, 2014, 26(6): 106-110. |
| [24] |
杨超, 李彦兰, 徐兵详, 等. 油水相对渗透率曲线非线性优化校正新方法及其应用. 石油与天然气地质, 2013, 34(3): 394-398. YANG C, LI Y L, XU B X, et al. New nonlinear correction method of oil-water relative permeability curves and their application. Oil & Gas Geology, 2013, 34(3): 394-398. DOI:10.11743/ogg20130317 |
 2017, Vol. 29
2017, Vol. 29



