0 引言

在5种基本类型的气体吸附等温线中，只有Ⅰ型等温线可以用Langmuir公式处理。其他4种类型等温线在中等压力后，吸附量都有明显增大的部分，表明有多层吸附的发生。从物理吸附力的本质是范德华力的角度来说，在固体表面吸附的第1层气体分子上进行第2层，乃至多层吸附完全是合理的。1938年，Brunauer等^[1]基于Langmuir单分子层吸附模型提出了一种多分子层吸附模型并推导出了BET公式，并使用BET公式的变形做出BET图，根据截距和斜率计算出了单分子层吸附量与吸附热有关的常数C。这为标准等温吸附曲线的研究打开了局面。之后通过15种已知的无孔材料的等温吸附曲线数据，利用BET原理做出了第1条正式的标准等温吸附曲线^[2]。

其他研究者认为每一组表面性质相似的固体需要1根标准等温线，并绘制了诸如石墨、金属氧化物、金属等不同种类的吸附剂样品各种标准等温曲线，并且分析了曲线图中低压和高压区异常的特征和原因^[3-6]。

再根据BET常数c的大小将氮、氧、氩、一氧化碳和二氧化碳在各种固体上的等温曲线分为5种标准曲线，借此反映出根据吸附剂和吸附质之间作用力强度(C值)的大小分类原则，至此，标准化等温吸附曲线不仅仅局限于基于吸附剂类型的分类^[7]。

陈诵英^[8-10]利用标准等温吸附曲线的统计特性，制定出一个完全无须作空模型假设即可计算孔径分布的新方法，并利用标准等温吸附曲线来表征多层吸附。应用该方法计算了12个样品的孔径分布并利用了它的2个基本特征来划分计算间隔的平均吸附层数且与BJH算法做了比较。之后应用常数C值选择了用于微孔结构分析的标准等温吸附曲线。用V-n做图法获得了样品的主要孔隙结构参数。并且根据常数C选用了合适的标准等温吸附曲线作为完全孔径分布的依据，获得了总孔表面积、微孔表面积和体积、非微孔表面积和体积以及平均微孔水力半径等主要孔隙结构参数，并获得了所有样品的完全孔径分布。

标准等温吸附曲线的概念提出较早，主要作为图版来使用，应用范围较小，使用方式较单一，因此在1990年以后就很少再用了。

国内外研究存在的问题有：①目前已有的研究主要侧重于无孔均质材料的研究，没有针对特定的多孔非均质材料的标准等温吸附曲线的研究。②目前的标准等温吸附曲线研究没有对毛细凝聚以后的吸附过程进行探究。故本次研究主要针对非均质多孔材料发生毛细凝聚后的标准等温吸附曲线进行探究。

1 页岩等温吸附曲线的影响因素

每个页岩储层都可获取大量的岩石样品，由于每个岩石样品的成分以及孔隙结构差异，所以每个岩石样品都有其独特的吸附特征，从而导致了它们的吸附曲线的形态各不相同。

本次研究的目的是找到一个地层里不同岩样的共性特征，从而得到整个地层的标准化等温吸附曲线，以在油藏数值模拟或油藏工程计算中进行应用。

页岩作为一种致密的储层，其成分复杂，包含多种黏土矿物：高岭石、伊利石、蒙脱石、绿泥石等；碎屑矿物：石英、长石、方解石等，以及不同类型的干酪根和少量黄铁矿等各种金属氧化物。因为不同矿物的晶体结构不同，物理化学性质也不同，所以每种成分和氮气分子之间的相互作用力都有其独特的特征，导致不同组分和氮气分子之间的吸附性能也各不相同^[11]。

同时页岩中不同矿物微观晶体形态的不同也导致了页岩中孔隙结构的复杂性。从孔隙形态来说，页岩中有圆柱形孔隙、平板形孔隙、楔形孔隙、墨水瓶形孔隙，当然还有一些孔隙形态不规则(图 1)。从孔隙大小来说，页岩的孔隙空间中大孔占有一定比例，但因为页岩的致密性，其孔隙空间中发育有大量微孔和介孔，所以页岩孔隙内吸附势能分布也具有显著的特殊性和多变性。

页岩复杂多变的成分和孔隙结构导致从不同页岩样品所得到的等温吸附曲线变化多端。如何找到一个地层中所得不同岩样的共性特征从而得到整个地层的标准化等温吸附曲线，以便在油藏数值模拟或油藏工程计算中进行应用是一个重要的论题，也是本次研究的目的。

2 页岩标准等温吸附曲线的建立 2.1 研究区概况

鄂尔多斯盆地延长组页岩发育在半深湖—深湖以及湖相淡水—微咸水环境中。鄂尔多斯盆地延长组页岩埋深较浅，最大埋深为1 700 m，平均埋深为1 288 m。其平均厚度为80 m，最大可达100 m。延长组岩性多为黑色、黑灰色、灰黑色、深灰色油页岩夹暗色泥岩、炭质泥岩、粉砂岩、铁质泥岩。

延长组页岩储层孔隙以中孔为主，并且多为纳米孔，其孔隙度极低，为0.40%~6.99%，平均值为3.05%。延长组主要有机质类型是Ⅱ₁和Ⅱ₂型，TOC质量分数为1.45%~7.20%，平均值为4.04%，有机质成熟度较低，为0.51%~1.25%^[12]。

2.2 标准等温吸附曲线建立的方法

1938年，Brunauer等^[1]将Langmuir单分子层吸附理论扩展到多分子层吸附，从经典统计理论导出了多分子层吸附公式，即BET公式

$ v = \frac{{{v_{\rm{m}}}cp}}{{({p_0} -p)\left[{1{\rm{ }} + (c-1)\frac{p}{{{p_0}}}} \right]}} $

(1)

式中：v为吸附量，mL/g；v_m为单分子层吸附量，mL/ g；p为压力，Pa；p₀为平衡压力，Pa；c为常数。

将式(1)变形可得

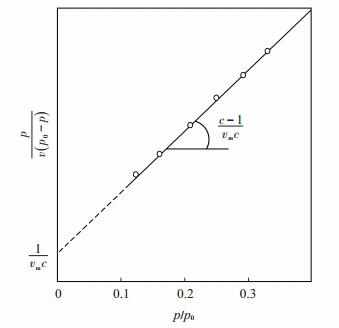
$ \frac{p}{{v({p_{\rm{o}}} -p)}} = \frac{1}{{{v_{\rm{m}}}c}} + \frac{{c -1}}{{{v_{\rm{m}}}c}}\frac{p}{{{p_0}}} $

(2)

由$ \frac{p}{{v({p_0} -p)}}$和$\frac{p}{{{p_0}}} $的关系可画出BET图(图 2)。

图中截距$h = \frac{1}{{{v_{\rm{m}}}c}} $, 斜率$k = \frac{{c -1}}{{{v_{\rm{m}}}c}} $。由此可求出

$ \left\{ \begin{array}{l} c = \frac{k}{h} + 1\\ {v_{\rm{m}}} = \frac{1}{{k + h}} \end{array} \right. $

(3)

根据此方法求得的单分子层最大吸附量，就可以用于等温吸附曲线标准化过程。单分子层吸附量还可以用于计算样品比表面积。

用等温吸附仪对鄂尔多斯盆地延长组长7油层组页岩储层的59个样品进行液氮等温吸附实验，并得到每个样品的标准等温吸附曲线。本次研究采用将吸附体积转化成吸附层厚度的方法对样品的等温吸附曲线进行标准化。

页岩储层的标准等温吸附曲线具体做法如下：

(1) 首先对该盆地所有样品的标准等温吸附曲线按照公式$t = \sigma \frac{V}{{{V_m}}} $进行标准化，得到每个样品的标准化等温吸附曲线。其中σ = 0.354 nm，是氮气单分子层的厚度。

(2) 其次将该盆地所有样品的标准等温吸附曲线按照BET理论中常数c的大小进行分类。

(3) 之后通过第1步所得的该盆地所有样品的标准化等温吸附曲线用De Bore，Halsey和Carbon Black吸附层厚度公式进行参数拟合。

(4) 最后将该盆地中每1个C值分组中所有样品的参数进行加权平均，得到每1个分组的标准等温吸附曲线$ t = f\left( {\frac{p}{{{p_0}}}} \right)$。

2.3 样品分类

标准化过程虽然已经增强了表面性质相似的页岩样品的吸附曲线形态的共性，但是地层中不同区域页岩性质的差异性太大，难以用一根曲线来概括整个盆地不同地层的吸附特征，所以须要对样品进行分类，并对每一分类建立各自的标准等温吸附曲线。

本次研究选用吸附剂与吸附质之间的相互作用力作为曲线分类的标准。BET等温多层吸附理论中的相互作用力是曲线分类的理论基础。BET理论中常数C的表达式为

$ C = \frac{{{a_1}}}{{{b_1}}}{{\rm{e}}^{\frac{{{E_1} -{E_L}}}{{RT}}}} $

(4)

式中：E₁为第1层的吸附热，kJ/mol；E_L为液体的蒸发热或凝聚热，kJ/mol；a₁，b₁为常数。$\frac{{{a_1}}}{{{b_1}}} $为比例系数，且$ \frac{{{a_1}}}{{{b_1}}} \approx 1$，则$C \approx {{\rm{e}}^{\frac{{{E_1} -{E_L}}}{{RT}}}} $。E₁代表了吸附剂和第1层吸附质分子之间的作用能。E₁越大，吸附剂和吸附质之间的作用力越大；E₁越小，吸附剂和吸附质之间的作用力越小。因此可推出，吸附作用力越大，E₁越大，C值也越大；吸附作用力越小，E₁越小，C值也越小。C值代表了吸附质和吸附剂之间相互作用力的强弱，因此用C值对盆地的样品进行分类。因为E₁位于C值表达式是在指数的分子上，因此C值和e的指数次幂成正比。又因为e ≈ 2.718，考虑到实际页岩样品的C值大约为0~600，为了使样品的分组不至于过少，所以选取2的指数分布对样品进行分组。在实验中发现，要使不同C值的等温吸附曲线在同一坐标系中分散均匀，那么C值大致是以指数形式分布的，因此将该盆地的样品以2的指数分布来进行分组(表 1)。

2.4 样品参数拟合

De Bore等^[3-6]，Halsey^[12]和Magee^[13]分别推导了其各自关于吸附层厚度的计算公式

$ \left\{ {\begin{array}{l} {\rm{De\;\; Bore厚度}}:t = {\left[{\frac{{13.99}}{{\ln \left( {\frac{p}{{{p_0}}}} \right) + 0.034}}} \right]^{\frac{1}{2}}}\\ {\rm{Halsey 厚度}}:t = 3.54{\left[{\frac{5}{{2.303\ln \left( {\frac{p}{{{p_0}}}} \right)}}} \right]^{\frac{1}{3}}}\\ {\rm{Carbon \;\;Black 厚度}}:{t_{{\rm{CB}}}} = 0.88{\left( {\frac{p}{{{p_0}}}} \right)^2} + 6.45\left( {\frac{p}{{{p_0}}}} \right) + 2.98 \end{array}} \right. $

(5)

式(5)是用Matlab软件进行参数拟合的公式原型。为了提高拟合精度，简化计算过程，将De Bore等^[3-6]，Halsey^[12]和Magee^[13]经验方程中的经验参数根据原始公式转换为可以通过实验数据求得的变量，而对Magee方程的吸附层厚度公式作了如下变形，因为Magee推导出的Carbon Black厚度方程原本就是个二次型的经验式，其方程的阶次主要是由于所选取的测试对象的固有属性确定的，二阶与三阶方程在本质上是没有差别的，只是其所适用的对象有所区别，所以将Carbon Black 2次方程拓展到了3次，其中$ x = \ln \left( {\frac{p}{{{p_0}}}} \right)$，a，b，c为待定参数

$ \left\{ \begin{array}{l} {\rm{De \;\;Bore 方程}}:t = {\left( {\frac{a}{{x + b}}} \right)^c}x = \ln \left( {\frac{p}{{{p_0}}}} \right)\\ {\rm{Halsey 方程}}:t = 3.54{\left( {\frac{a}{x}} \right)^b}x = \ln \left( {\frac{p}{{{p_0}}}} \right)\\ {\rm{Carbon\;\; Black\;\; 2 次方程}}:{t_{{\rm{CB}}}} = a{x^2} + bx + cx = \frac{p}{{{p_0}}}\\ {\rm{Carbon\;\; Black\;\; 3 次方程}}:{t_{{\rm{CB}}}} = a{x^3} + b{x^2} + cx + dx = \frac{p}{{{p_0}}} \end{array} \right. $

(6)

用Matlab软件对盆地所有样品进行参数拟合，就能得到每条曲线的吸附层厚度公式$ x = f\left( {\frac{p}{{{p_0}}}} \right)$。

2.5 参数平均化

因为3种数学模型拟合的精度都很高，说明和原数据的重合性很强，因此拟合后的参数平均的还原度能够较高的体现这一分组的吸附特征。在页岩标准等温吸附曲线的建立过程中，也可以用较为便捷的方法，即先对所有样品的吸附曲线进行平均，并用平均的等温吸附曲线标准化拟合参数得出标准等温吸附曲线，但因为试验中每个压力点都有微小的差距(比如相对压力约为0.5时，不同样品测的稳定压力点不同，有0.47，0.48，0.51，0.52等)，这本质上就导致了一次计算的误差，并且可能导致平均的等温吸附曲线在低压区会有微小的波动，曲线不流畅平滑。所以选用较为繁琐但是精确性更高的方法来求取标准等温吸附曲线。

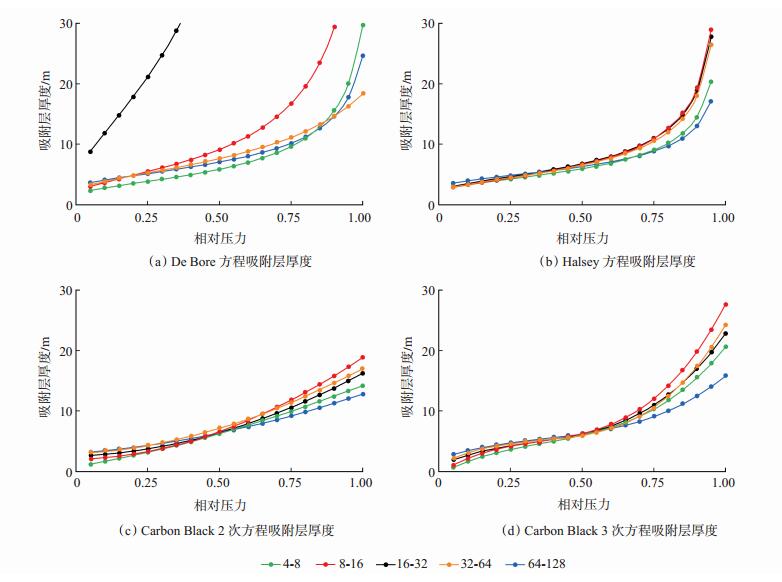
将盆地中每一分组样品的拟合参数进行平均，就可得到每一分组的标准等温吸附曲线(图 3)。从图 3中可以看出，4种吸附层厚度数学模型拟合出的曲线都有其独特的形态特征，但大体趋势相差不大。值得注意的是，这4种类型的拟合曲线都在相对压力大约0.4的时候发生了交叉。在相对压力小于0.4的时候，每种类型的曲线有非常明显的规律性，即c值越大，吸附曲线越靠上，吸附层厚度越厚，吸附性能越强。说明c值越大，则相同相对压力下的吸附层厚越大，这充分验证了c值越大，吸附性能越强的原则。在相对压力大于0.4之后，曲线出现了无序且吸附层厚度瞬间大幅上升的情况，这是因为多孔材料在相对压力大于0.4之后就会发生毛细凝聚现象，增加的部分为发生毛细凝聚的气体在多孔内瞬时从气相转化为液相的部分。发生毛细凝聚后，已经填充满的孔隙内就不再发生吸附，不再对吸附层的厚度有贡献。计算吸附层厚度时所用的仍然是所有孔隙的单分子层吸附量，由于每个样品的孔径分布都各不相同，导致平均标准化曲线在相对压力大于0.4之后出现了乱序。

2.6 拟合参数和精度分析

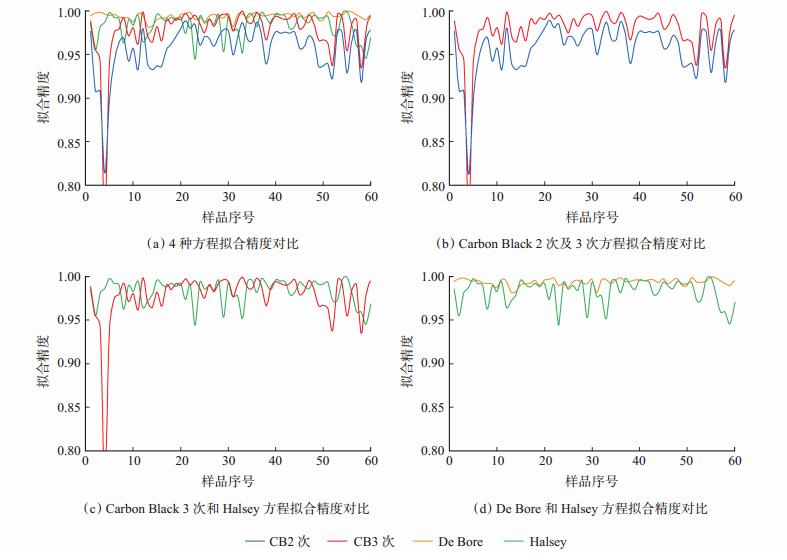
将鄂尔多斯盆地59块样品4种吸附层厚度模型的拟合精度(均方差值)进行对比(图 4)。可以明显看出，4种吸附层厚度公式模型的拟合精度都> 0.9。其中De Bore方程吸附层厚度模型的拟合精度明显高于其他模型，Carbon Black 2次方程的拟合精度是最低的。

在[图 4(b)]中，将Carbon Black 2次和Carbon Black 3次方程进行对比，可以明显看出Carbon Black 2次和Carbon Black 3次方程拟合精度变化的步调非常一致，但Carbon Black 3次方程的拟合精度明显高于Carbon Black 2次方程。

[图 4(c)]中将排在第2，3位的Halsey方程和Carbon Black 3次方程单独对比，可以看出这两者的拟合精度相差不大，但Halsey方程拟合精度的稳定性要高于Carbon Black 3次方程。

[图 4(d)]中又将De Bore和Halsey方程进行比较，可以看出，De Bore方程的拟合精度在0.98左右波动，拟合精度非常高，Halsey方程的拟合精度则在0.96左右波动，虽然精度依然很高，但是相比于De Bore方程的精度和波动性来说，仍然是De Bore方程的拟合精度更高。

综上所述，这4种方程的拟合精度从小到大排列为Carbon Black 2次方程＜Carbon Black 3次方程＜Halsey方程＜De Bore方程。

下面对每种吸附层厚度模型的参数进行对比分析(图 5)。De Bore方程中参数a的大部分值为0~50，局部波动范围相对较大；参数b为0~0.1，参数c为0.2~0.8，二者波动范围都很小。Halsey方程中参数a为0~5，参数b为0~1。可以看出参数a，b的变化范围都很小。Carbon Black 2次方程中参数a为0~10，参数b为0~10。参数c局部区域波动稍大，但仍为0~10。综上所述，这4种吸附层厚度模型的参数变化范围都不大，因此也验证了，用参数平均的方法来求取标准等温吸附曲线的方法是可行的。

3 结论

(1) BET理论中的常数 C能够综合体现页岩的吸附能力，C值越大，则吸附能力越强，等温吸附曲线越靠上；反之，C 值越小，吸附性能越差，等温吸附曲线越靠下。

(2) 对来自鄂尔多斯的页岩样品分别用相对压力和吸附层厚度的关系进行标准化。并且用Matlab软件对这59块样品的标准化曲线分别用De Bore吸附层厚度方程、Halsey吸附层厚度方程、Carbon Black 2次吸附层厚度方程和Carbon Black 3次吸附层厚度方程进行参数拟合，拟合精度都比较高。

(3) 4种吸附层厚度方程拟合精度从小到大排列为Carbon Black 2次方程＜Carbon Black 3次方程＜Halsey方程＜De Bore方程。