2. 中海油田服务股份有限公司油田生产研究院, 天津 300459
2. Research Institute of Production Optimization, China Oilfield Services Limited, Tianjin 300459, China
水力压裂是开发致密储层的必要手段,而储层原始地层压力和有效渗透率均是对此类储层进行储层评价、压裂设计和压后配产的重要参数。由于应用传统的压前及压后压力恢复试井获取致密储层原始地层压力和有效渗透率需要十分漫长的关井测试时间,所以其适用性较差[1-5]。虽然利用常规的小型压裂压降测试方法(DFIT方法,Diagnostic Fluid Injection Tests)获取储层参数相较于传统的试井方法明显地缩短了测试时间[6-7],但仍然需要压后观测压降数十小时[8-10],因此依然难以适用于现场;同时该方法还要求小液量(< 10 m3),低排量(< 500 L/min)压开地层以缩短拟径向流的出现时间[11-12],因而无法达到通过小型压裂认识裂缝扩展特点的目的[13]。针对以上问题,提出一种利用小型压裂停泵后短时间压降数据快速获取致密储层原始地层压力和有效渗透率的新方法,并结合实例计算验证该方法的现场适用性与可靠性,以期促进致密储层的高效开发。
1 利用小型压裂快速获取储层原始地层压力的新方法小型压裂裂缝闭合后的压力降落存在拟线性流和拟径向流2个特征阶段[6]。裂缝闭合后裂缝向地层的渗流会较快地出现拟线性流[14],但拟径向流阶段的出现却往往需要较漫长的压降观测时间。现场小型压裂的压降观测时间一般为1~2 h,因此这里提出可以应用裂缝闭合后拟线性流阶段的压降特征快速获取储层的原始地层压力。
在拟线性流阶段由于储层不稳定流和热传导间的相似性,可采用Carslaw等[15]给出的关于热传导的相似条件,将拟线性流压降方程表示为
| $ {P_{\rm{w}}}\left( t \right) - {P_{\rm{i}}} = {C_{\rm{L}}}\sqrt {\frac{{{\rm{ \mathsf{ π} }}\mu }}{{k\varphi {c_{\rm{t}}}}}} \left( {\frac{2}{{\rm{ \mathsf{ π} }}}\arcsin \sqrt {\frac{{{t_{\rm{c}}}}}{t}} } \right) $ | (1) |
式中:Pw(t)为停泵后井底压力,MPa;Pi为储层原始地层压力,MPa;CL为储层滤失系数,m/min0.5;μ为滤失液体黏度,mPa·s;k为储层有效渗透率,D;φ为储层孔隙度,无因次;ct为储层综合压缩系数,MPa-1;tc为闭合时间(包括泵注时间),min;t为小型压裂时间(包括泵注时间和压降观测时间),min。
Nolte [6]在引入FL(t)函数的基础上将式(1)简化为
| $ {P_{\rm{w}}}\left( t \right) - {P_{\rm{i}}} = {m_{\rm{L}}}\sqrt {F_{\rm{L}}^2\left( t \right)} $ | (2) |
其中:
| $ {m_{\rm{L}}} = {C_{\rm{L}}}\sqrt {\frac{{{\rm{ \mathsf{ π} }}\mu }}{{k\varphi {c_{\rm{t}}}}}} $ | (3) |
| $ {F_{\rm{L}}}\left( t \right) = \frac{2}{{\rm{ \mathsf{ π} }}}\arcsin \sqrt {\frac{{{t_{\rm{c}}}}}{t}} $ | (4) |
由式(2)可得,利用裂缝闭合后的井底压力作Pw(t) - Pi与FL2(t)的双对数曲线,通过在曲线上获取斜率为0.5的直线段即可识别拟线性流。由于式(2)中储层原始地层压力Pi也是未知参数,其取值的差异对曲线斜率有较大影响进而干扰裂缝闭合后拟线性流压降阶段的识别,因此,这里提出将式(2)两边对FL2(t)求导并乘以FL2(t)以得到
| $ F_{\rm{L}}^2\left( t \right)\frac{{{\rm{d}}\left[ {{P_{\rm{w}}}\left( t \right) - {P_{\rm{i}}}} \right]}}{{{\rm{d}}\left[ {F_{\rm{L}}^2\left( t \right)} \right]}} = F_{\rm{L}}^2\left( t \right)\frac{{{\rm{d}}\left[ {{P_{\rm{w}}}\left( t \right)} \right]}}{{{\rm{d}}\left[ {F_{\rm{L}}^2\left( t \right)} \right]}} = 0.5{m_L}\sqrt {F_{\rm{L}}^2\left( t \right)} $ | (5) |
再对式(5)两边取对数,可得
| $ \lg \left\{ {F_{\rm{L}}^2\left( t \right)\frac{{{\rm{d}}\left[ {{P_{\rm{w}}}\left( t \right)} \right]}}{{{\rm{d}}\left[ {F_{\rm{L}}^2\left( t \right)} \right]}}} \right\} = 0.5\lg F_{\rm{L}}^2\left( t \right) + \lg \left( {0.5{m_L}} \right) $ | (6) |
根据式(6)作
小型压裂过程中液体不断向地层滤失,而停泵后液体滤失并造成裂缝压力向地层扩散是导致井底压降的直接原因。因此,提出通过分析小型压裂的液体滤失过程来模拟压后压降曲线,并将之与实际曲线进行拟合以快速获取储层有效渗透率。
2.1 小型压裂液体滤失计算模型的建立由于小型压裂常采用KCl溶液施工而难以形成有效滤饼,因此根据连续性方程和达西定律,并考虑泵注液体在地层中的二维流动[16],可得到液体向地层滤失的微分方程,即
| $ \frac{{\partial P}}{{\partial x}}\left( {\frac{k}{\mu }\frac{{\partial P}}{{\partial x}}} \right) + \frac{{\partial P}}{{\partial y}}\left( {\frac{k}{\mu }\frac{{\partial P}}{{\partial y}}} \right) = {c_{\rm{t}}}\varphi \frac{{\partial P}}{{\partial t}} $ | (7) |
式中:P为储层网格压力,MPa。
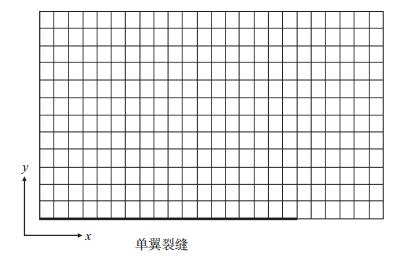
为了利用式(7)表征小型压裂过程中液体向地层的滤失行为,需要对裂缝-储层系统进行网格划分。由于裂缝-储层系统的对称性,可取1/4储层为研究单元划分x-y方向的均匀网格(图 1)。
|
下载eps/tif图 图 1 人工裂缝-储层网格系统的划分 Fig. 1 Meshing of the created fracture-reservoir system |
在网格划分的基础上对式(7)进行数值差分可以得到
| $ {a_{i,j}}{P_{i,j - 1}} + {b_{i,j}}{P_{i - 1,j}} + {c_{i,j}}{P_{i,j}} + {d_{i,j}}{P_{i + 1,j}} + {e_{i,j}}{P_{i,j + 1}} = {g_{i,j}} $ | (8) |
其中:
| $ \left\{ \begin{array}{l} {a_{i,j}}={\left( {\frac{k}{\mu }} \right)_{i,j - \frac{1}{2}}}\frac{1}{{0.5\left( {\Delta {y_j} + \Delta {y_{j - 1}}} \right)\Delta {y_j}}}\\ {b_{i,j}}={\left( {\frac{k}{\mu }} \right)_{i - \frac{1}{2},j}}\frac{1}{{0.5\left( {\Delta {x_i} + \Delta {x_{i - 1}}} \right)\Delta {x_i}}}\\ {d_{i,j}}={\left( {\frac{k}{\mu }} \right)_{i + \frac{1}{2},j}}\frac{1}{{0.5\left( {\Delta {x_{i + 1}} + \Delta {x_i}} \right)\Delta {x_i}}}\\ {e_{i,j}}={\left( {\frac{k}{\mu }} \right)_{i,j + \frac{1}{2}}}\frac{1}{{0.5\left( {\Delta {y_{j + 1}} + \Delta {y_j}} \right)\Delta {y_j}}}\\ {c_{i,j}} = - \left( {{a_{i,j}} + {b_{i,j}} + {d_{i,j}} + {e_{i,j}}} \right) - \frac{{{c_{\rm{t}}}\varphi }}{{\Delta t}}\\ {g_{i,j}} = \frac{{ - {c_{\rm{t}}}\varphi p_{i,j}^n}}{{\Delta t}} \end{array} \right. $ | (9) |
式中:Δx为x方向的储层网格长度,m;Δy为y方向的储层网格长度,m;Δt为时间步长,s。
液体向地层的滤失会引起裂缝压力向地层扩散。利用式(8)~ (9)建立对五角方程组[17]即可求得小型压裂过程中某一井底压力下一时步的地层压力扩散情况。为了求解该方程组,还需定义模型的边界条件及初始条件。对于致密储层,可定义封闭外边界条件为
| $ \left\{ \begin{array}{l} \frac{{\partial P}}{{\partial y}}\left| {_{y = {L_y}}} \right. = 0\\ \frac{{\partial P}}{{\partial x}}\left| {_{x = {L_x}}} \right. = 0 \end{array} \right. $ | (10) |
由于划分储层的对称性,可定义内边界条件为停泵前:
| $ \left\{ \begin{array}{l} P\left| {_{x \le {L_{\rm{f}}}\left( t \right),y = 0}} \right. = {P_{\rm{f}}}\\ \frac{{\partial P}}{{\partial x}}\left| {_{x = 0,y = 0 \sim {L_y}}} \right. = 0\\ \frac{{\partial P}}{{\partial y}}\left| {_{y = 0,x = {L_{\rm{f}}}\left( t \right) \sim {L_x}}} \right. = 0 \end{array} \right. $ | (11) |
停泵后:
| $ \left\{ \begin{array}{l} P\left| {_{x \le {L_{\rm{p}}},y = 0}} \right. = {P_{\rm{w}}}\\ \frac{{\partial P}}{{\partial x}}\left| {_{x = 0,y = 0 \sim {L_y}}} \right. = 0\\ \frac{{\partial P}}{{\partial y}}\left| {_{y = 0,x = {L_{\rm{p}}} \sim {L_x}}} \right. = 0 \end{array} \right. $ | (12) |
式中:Pf为泵注过程中的井底压力,MPa;Lf(t)为泵注过程中的单翼缝长,m;Lp为停泵后的单翼缝长;m,Lx为x方向的储层长度,m;Ly为y方向的储层长度,m。
在小型压裂施工之前,地层处于原始状态,因此初始条件为
| $ P\left| {_{t = 0}} \right. = {P_{\rm{i}}} $ | (13) |
小型压裂可分为泵注和压后压降2个阶段,而模拟小型压裂停泵后压降曲线需以停泵时的储层压力分布为基础。由式(11)~ (12)可知,在泵注阶段的内边界条件中Lf随时间变化,属于动态边界,而泵注过程中每个时间点的裂缝延伸方程可用下式[18]表示:
| $ {L_{\rm{f}}}\left( t \right) = {L_{\rm{p}}}{\left( {\frac{t}{{{t_{\rm{p}}}}}} \right)^e} $ | (14) |
式(14)中停泵时的单翼缝长Lp可利用裂缝闭合前拟三维压降分析方法[19]进行求解,即
| $ {L_{\rm{p}}} = \frac{Q}{{\frac{{\rm{ \mathsf{ π} }}}{4}{H_{\rm{w}}}{W_{\max }}\left( {\frac{{1.01{H_{\rm{p}}}}}{{{H_{\rm{w}}}}} + \frac{1}{z}\arcsin z} \right){\beta _{\rm{s}}} + \frac{{16}}{3}{C_{\rm{L}}}{H_{\rm{p}}}\sqrt {{t_{\rm{p}}}} }} $ | (15) |
式中:tp为小型压裂泵注时间,min;Q为总注液量,m3;Hw为停泵时缝高,m;Wmax为停泵时最大当量缝宽,m;Hp为储层滤失高度,m;βs为停泵后缝内压力与井底压力比;z为中间参数,
根据拟三维压后压降分析方法,式(15)中的Wmax,Hw,CL可由下式[19-20]求得:
| $ \begin{array}{l} {W_{\max }} = \frac{{2\left( {1 - {\upsilon ^2}} \right){H_{\rm{w}}}}}{E}\left( {ISIP - {S_1}} \right) - \frac{{4\left( {1 - {\upsilon ^2}} \right){H_{\rm{w}}}}}{{{\rm{ \mathsf{ π} }}E}} \cdot \\ \;\;\;\;\;\;\;\;\;\;\Delta S\left( {\arccos \frac{{{H_{\rm{p}}}}}{{{H_{\rm{w}}}}} - \frac{{{H_{\rm{p}}}}}{{{H_{\rm{w}}}}}\ln \frac{{{H_{\rm{w}}} + \sqrt {H_{\rm{w}}^2 - H_{\rm{p}}^2} }}{{{H_{\rm{p}}}}}} \right) \end{array} $ | (16) |
| $ ISIP - {S_1} = \sqrt {\frac{2}{{{\rm{ \mathsf{ π} }}{H_{\rm{w}}}}}} {K_1} + \frac{2}{{\rm{ \mathsf{ π} }}}\Delta S\arccos \frac{{{H_{\rm{p}}}}}{{{H_{\rm{w}}}}} $ | (17) |
| $ {C_{\rm{L}}} = \frac{{{\rm{ \mathsf{ π} }}H_{\rm{w}}^2{\beta _{\rm{s}}}M\left( {1 - {\upsilon ^2}} \right)}}{{8E{H_{\rm{p}}}\sqrt {{t_{\rm{p}}}} }}\left( {\frac{{1.01{H_P}}}{{{H_W}}} + \frac{1}{z}\arcsin z} \right){p^ * } $ | (18) |
式中:E为杨氏模量,MPa;υ为泊松比;ISIP为井底瞬时停泵压力,MPa;S1为储层最小水平主应力,MPa;KI为应力强度因子[20];ΔS为隔层与储层最小水平主应力差值,MPa;p*为拟合压力,MPa。
在式(14)中,除Lp外,裂缝延伸指数e也是未知参数。对于拟三维裂缝模型,当泵注的液体效率η趋于0和100%时,对应的e分别为0.5和
| $ e = 0.5 + \eta \left( {\frac{{2n + 2}}{{2n + 3}} - 0.5} \right) $ | (19) |
式中:n为注入液体的流变指数。
式(19)中的小型压裂液体效率η可用下式[22]进行简便计算:
| $ \eta \approx \frac{{{G^ * }}}{{2 + {G^ * }}} $ | (20) |
其中:
| $ {G^ * } = \frac{{ISIP - {P_{\rm{c}}}}}{{\left( {\frac{{{\rm{d}}{P_{{\rm{w}},0.75}}}}{{{\rm{d}}G}}} \right)}},{P_{{\rm{w}},0.75}} = 0.75\left( {ISIP - {P_{\rm{c}}}} \right) + {P_{\rm{c}}} $ | (21) |
式中:Pc为裂缝闭合压力,MPa。
根据式(15) ~ (21)可求得Lp和e,进而得到泵注阶段裂缝延伸方程,再结合停泵前每一时步的井底泵注压力Pfn,即可根据前文建立的液体滤失计算模型对停泵瞬间的储层压力分布进行数值模拟。在此基础上,再根据液体滤失计算模型求解小型压裂停泵后不同井底压力Pwn下的地层网格压力,然后基于达西定律就可计算停泵后每一时步的液体总滤失量:
| $ V_{{\rm{loss}}}^n = V_{{\rm{loss}}}^{n - 1} + 4\Delta t\sum\limits_{i = 0}^m {\frac{k}{\mu }\frac{{P_{\rm{w}}^n - P_{{\rm{i,1}}}^n}}{{\Delta {y_1}}}{l_{xi}}{H_{\rm{p}}}} $ | (22) |
式中:m为裂缝划分的网格数,个;Pi, 1为裂缝邻近的地层网格压力,MPa;Δy1为y方向第一排网格长度,m;lxi为裂缝x方向网格的长度,m。
由前文小型压裂液体滤失计算模型及式(22)可知,在压降过程中井底压力Pwn不断变化并相应地改变储层压力分布,从而改变液体滤失量,所以停泵后的液体总滤失量Vlossn是Pwn的函数。
在利用式(15)~ (18)求得停泵时缝长和缝高的基础上,停泵后裂缝的体积变化量可以由下式[19]表示:
| $ \begin{array}{l} \Delta V_{\rm{f}}^n = \frac{{\rm{ \mathsf{ π} }}}{4}{H_{\rm{w}}}{L_{\rm{p}}}\left( {\frac{{1.01{H_P}}}{{{H_W}}} + \frac{1}{z}\arcsin z} \right){\beta _S}\left[ {{W_{\max }} - {W_{\max }}\left( {{t_{\rm{n}}}} \right)} \right]\\ \;\;\;\;\;\;\; = \frac{{{\rm{ \mathsf{ π} }}\left( {1 - {\upsilon ^2}} \right)}}{{2E}}H_{\rm{w}}^2{L_{\rm{p}}}\left( {\frac{{1.01{H_P}}}{{{H_W}}} + \frac{1}{z}\arcsin z} \right) \cdot \\ \;\;\;\;\;\;\;\;\;\;{\beta _S}\left( {ISIP - P_{\rm{w}}^n} \right) \end{array} $ | (23) |
从式(23)可以看出,停泵后裂缝体积变化量也是Pwn的函数。由于在关井期间裂缝体积变化量等于停泵后的液体总滤失量,因此可得出下式:
| $ \Delta V_{\rm{f}}^n\left( {P_{\rm{w}}^n} \right) = V_{{\rm{loss}}}^n\left( {P_{\rm{w}}^n} \right) $ | (24) |
若取较小的时间步长,则可利用Pwn - 1计算出Vlossn-1以近似代替Vlossn,进而根据式(24)得到下一时步的井底压力Pwn,如此反复迭代,即可模拟停泵后的整个压降过程。因此,在利用前文方法获得储层原始压力,并由式(14)~ (21)求得停泵时缝长、缝高及裂缝延伸方程后,再结合岩石力学参数等储层基础数据,就可通过调节储层有效渗透率这一单一变量以模拟得到不同的压后压降曲线。将其与实际曲线进行拟合,当拟合程度较高时即可获得实际的储层有效渗透率。
3 实例计算分析SM-7井位于鄂尔多斯盆地东部某致密砂岩气区块,该井本溪组储层在主压裂之前进行了小型压裂压降测试。利用本文方法对其进行实例计算与分析,其基础数据如表 1所列。
|
|
下载CSV 表 1 SM-7井本溪组储层小型压裂基础数据 Table 1 Basic data about mini-fracturing of Benxi Formation in well LM-7 |
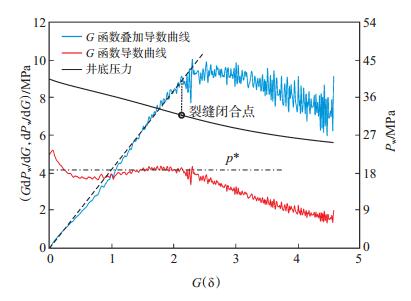
由上文可知,利用小型压裂短时间压降数据快速获取储层原始地层压力的关键在于准确识别裂缝闭合后的拟线性流。因此,绘制了SM-7井小型压裂压降G函数特征曲线以获取裂缝闭合点(图 2)。
|
下载eps/tif图 图 2 G函数特征曲线 Fig. 2 G function characteristic curves |
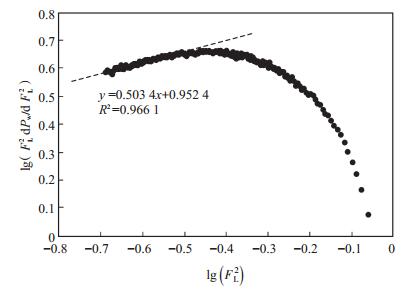
从图 2可看出,SM-7井小型压裂的人工裂缝闭合时间为20.2 min。根据本文方法利用人工裂缝闭合后压降数据作
|
下载eps/tif图 图 3 裂缝闭合后拟线性流识别曲线 Fig. 3 Identification curve for the quasi-linear |
|
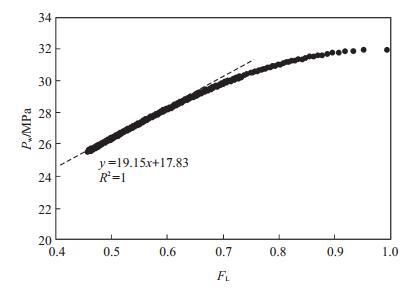
下载eps/tif图 图 4 裂缝闭合后Pw - FL曲线 Fig. 4 Pw - FL curve after fracture closure |
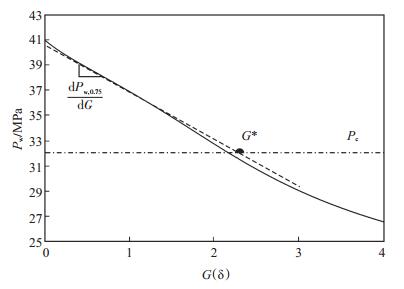
根据本文方法,求取储层有效渗透率需先求得停泵时裂缝的几何尺寸及泵注阶段裂缝的延伸方程。由图 1可得拟合压力p* = 4.21 MPa,结合表 1数据及式(15)~ (18)可计算得到停泵时井底缝高为10.5 m,单翼缝长为63.1 m,最大缝宽为6.5 mm。根据式(21)绘制Pw -G曲线(图 5)。由图 5可得G* = 2.35,将其带入式(19)和式(20)可得到裂缝延伸指数e= 0.66,进而可由式(14)得到泵注过程中单翼缝长随时间变化的表达式:
| $ {L_{\rm{f}}}\left( t \right) = 63.1{\left( {\frac{t}{{10}}} \right)^{0.66}} $ | (25) |
|
下载eps/tif图 图 5 Pw - G曲线 Fig. 5 Pw - G curve |
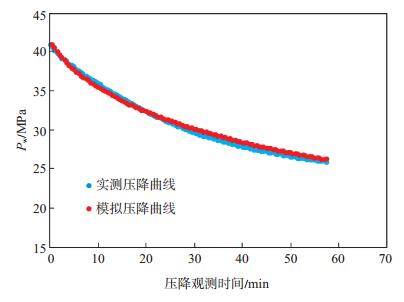
在求得储层原始地层压力、停泵时缝长和缝高以及泵注阶段裂缝延伸方程后,再结合表 1基础数据,即可假定储层有效渗透率模拟小型压裂停泵前、后的液体滤失及储层压力扩散过程以得到相应的压后压降模拟曲线。通过调节储层有效渗透率这一单一变量使模拟曲线与实测曲线达到最佳拟合(图 6)。
|
下载eps/tif图 图 6 压后压降拟合曲线 Fig. 6 Fitting of pressure drop curve at post-fracturing |
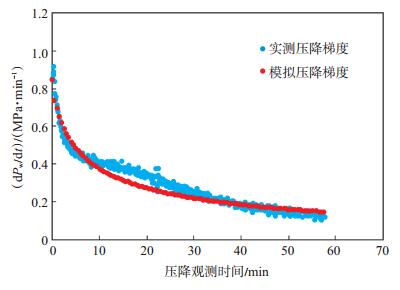
从图 6可以看出,当调节储层有效渗透率为0.28 mD时,模拟压降曲线与实测压降曲线达到最佳拟合。再绘制模拟压降梯度与实测压降梯度的拟合曲线(图 7)。从图 7可看出,模拟压降梯度与实测压降梯度的吻合度较高,说明模拟的压降过程能够较好地反映实际情况。
|
下载eps/tif图 图 7 压后压降梯度拟合曲线 Fig. 7 Fitting of the pressure drop gradient curve at post-fracturing |
SM-7井本溪组在压前进行了压力恢复试井并得到储层原始地层压力与有效渗透率分别为17.90 MPa和0.21 mD,与利用本文方法所得结果相近。邻井同层位岩心实验测得储层岩石渗透率为0.013~0.420 mD,与本文结果相符,说明本文方法具有较高的可靠性。此外,为了获取储层物性参数,该井本溪组压前压力恢复试井共耗时135 h,类似储层采用常规小型压裂压降测试方法需在小注液量(< 10 m3)的前提下停泵观测压降24 h以上[11],而利用本文方法在小型压裂停泵后观测压降61 min即得到了目标参数,说明了本文方法可较大幅度地节约施工成本并提高作业效率。
4 结论(1) 提出了通过准确识别小型压裂裂缝闭合后拟线性流压降数据以快速获取致密储层原始地层压力的方法,实例计算结果表明该方法可利用短时间的小型压裂压降数据获取目标参数,并具有较高的准确性。
(2) 提出了通过分析小型压裂液体滤失过程进而模拟停泵后压降曲线,并将其与实测压降曲线进行拟合以获取致密储层有效渗透率的方法。实例计算结果表明,该方法不要求小液量、低排量的小型压裂施工,在小型压裂压降观测时间较短的情况下即可应用,且计算结果具有较高的可靠性。
(3) 利用本文方法获取致密储层物性参数相比于传统的试井方法和常规的小型压裂压降测试方法可大幅缩短施工时间与施工成本,具有较强的现场适用性。建议在致密油气藏探井及重点井的主压裂施工前结合该方法进行小型压裂分析并进一步优化压裂施工参数,从而促进致密储层的高效开发。
| [1] |
马勇新, 雷霄, 张乔良, 等. 低渗透油藏有效渗透率计算新模型——以珠江口盆地海相低渗透砂岩为例. 岩性油气藏, 2016, 28(1): 117-122. MA Y X, LEI X, ZHANG Q L, et al. A new model for calculating effective permeability in low permeability reservoir:a case study of low permeability marine sediments reservoir in the Pearl River Mouth Basin. Lithologic Reservoirs, 2016, 28(1): 117-122. |
| [2] |
尹帅, 丁文龙, 单钰铭, 等. 利用致密砂岩储层电导率参数求取渗透率. 岩性油气藏, 2016, 28(6): 117-124. YIN S, DING W L, SHAN Y M, et al. Permeability calculation of tight sandstone reservoir by conductivity parameters. Lithologic Reservoirs, 2016, 28(6): 117-124. |
| [3] |
MAYERHOFER M J, EHLIG-ECONOMIDES C A, ECONOMIDES M J. Pressure transient analysis of fracture calibration tests. Journal of Petroleum Technology, 1995, 47(3): 229-234. DOI:10.2118/26527-PA |
| [4] |
EWENS S D, IDORENYIN E H, DONNELL P O, et al. Executing minifrac tests and interpreting after-closure data for determining reservoir characteristics in unconventional reservoirs. SPE 162779, 2012. |
| [5] |
杜军社, 李培俊, 万文胜, 等. 试井资料在压裂效果评价中的应用. 新疆石油地质, 2004, 25(4): 433-435. DU J S, LI P J, WAN W S, et al. Application of well test data to evaluation of hydraulic fracturing performance. Xinjiang Petroleum Geology, 2004, 25(4): 433-435. |
| [6] |
NOLTE K G. Background for after-closure analysis of fracture calibration tests. SPE 39407, 1997. |
| [7] |
侯晓春, 王建平, 张文中, 等. 运用小型压裂测试确定储层参数新方法. 大庆石油地质与开发, 2006, 25(2): 54-56. HOU X C, WANG J P, ZHANG W Z, et al. New method to determine reservoir parameters with the application of mini frac. Petroleum Geology & Oilfield Development in Daqing, 2006, 25(2): 54-56. |
| [8] |
PORCU M M, RETNANTO A R, ECONMIDES M J, et al. Comprehensive fracture calibration test design. SPE 168634, 2014. |
| [9] |
BARREE R D, MISKIMINS J L, GILBERT J V. Diagnostic fracture injection tests:Common mistakes, misfires, and misdiagnoses. SPE 169539, 2014. |
| [10] |
IBRAHIM M, PIEPRZICA C. Appraising unconventional play from mini-frac test analysis, actual field case. SPE 181465, 2016. |
| [11] |
张逸群, 余刘应, 张国锋. 基于微注入压降测试的页岩气储层快速评价方法. 石油钻探技术, 2017, 45(3): 107-112. ZHANG Y Q, YU L Y, ZHANG G F. Rapid evaluation of shale reservoirs based on pre-fracinjection/falloff diagnostic test. Petroleum Drilling Techniques, 2017, 45(3): 107-112. |
| [12] |
张文昌, 胡永全, 赵金洲, 等. 校准测试闭合后压降分析. 断块油气田, 2010, 17(1): 85-87. ZHANG W C, HU Y Q, ZHAO J Z, et al. Analysis after closure with calibration test. Fault-Block Oil & Gas Field, 2010, 17(1): 85-87. |
| [13] |
HARTING T A, COX D L, MURILLO R. Application of minifalloff test to determine reservoir parameters and optimize fracture designs in a tight gas field. SPE 90455, 2004. |
| [14] |
赵志红, 魏瑞, 梁豪. 水平井分段压裂测试获取地层参数. 油气井测试, 2015, 24(3): 31-34. ZHAO Z H, WEI R, LIANG H. Multi-stage fracturing and test in horizontal well to acquire formation parameter. Well Testing, 2015, 24(3): 31-34. |
| [15] |
CARSLAW H S, JEAGER J C. Conduction of heat in solid. Oxford: Oxford University Press, 1959, 225-227.
|
| [16] |
敬季昀. 水平井压后排液与支撑剂回流控制研究. 成都: 西南石油大学, 2014. JING J Y. The study of fluid flowback and proppant backflow for horizontal well fracturing. Chengdu: Southwest Petroleum University, 2014. |
| [17] |
韩大匡, 陈钦雷, 闫存章. 油藏数值模拟基础. 北京: 石油工业出版社, 1993, 131-133. HAN D K, CHEN Q L, YAN C Z. Reservoir numerical simulation. Beijing: Petroleum Industry Press, 1993, 131-133. |
| [18] |
NOLTE K G. A general analysis of fracturing pressure decline with application to three models. SPE 12941, 1986. |
| [19] |
王鸿勋, 张士诚. 水力压裂设计数值计算方法. 北京: 石油工业出版社, 1998, 247-250. WANG H X, ZHANG S C. Numerical calculation method for hydraulic fracturing design. Beijing: Petroleum Industry Press, 1998, 247-250. |
| [20] |
郭大立, 赵金洲, 郭建春, 等. 压裂后压降分析的三维模型和数学拟合方法. 天然气工业, 2001, 21(5): 49-52. GUO D L, ZHAO J Z, GUO J C, et al. Three-dimensional model and mathematical fitting method of pressure test data after fracturing. Natural Gas Industry, 2001, 21(5): 49-52. |
| [21] |
ECONOMIDES M J, NOLTE K G. Reservoir stimulation 3rd Edition. Englewood Cliffs: Prentice Hall, 2000, 318-319.
|
| [22] |
NOLTE K G. Fracturing-pressure analysis for nonideal behavior. Journal of Petroleum Technology, 1991, 43(2): 210-218. DOI:10.2118/20704-PA |
 2018, Vol. 30
2018, Vol. 30



