2. 中国石油勘探开发研究院, 北京 100083;
3. 中国石油经济技术研究院, 北京 100724;
4. 中国石油集团东方地球物理勘探有限责任公司, 河北 涿州 072750
2. PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China;
3. PetroChina Research Institute of Economics & Technology, Beijing 100724, China;
4. Bureau of Geophysical Prospecting, PetroChina, Zhuozhou 072750, China
近年来,随着非常规油气资源占比的增加,其勘探开发逐渐引起关注[1]。致密油作为一种重要的非常规能源,继页岩气之后已成为非常规油气勘探开发的新热点[2]。我国致密油气的勘探已取得明显成效[3-4],在准噶尔、鄂尔多斯、四川、渤海湾、松辽等盆地均发现了致密油油田。尽管致密油勘探已取得良好开端,但致密储层具有孔渗条件差、单井产能低[5-6]等特点,采用常规开发手段难以获得工业油气流。在国内,长庆油田率先利用“水平井+体积压裂”技术对致密油藏进行先导试验开发,并取得了良好的效果[7-9]。
目前,国内外针对水平井体积压裂参数优化设计的研究较少,且采用的模拟网格及假设条件多存在局限性和不适用性[10-11],难以精确表征储层中的天然裂缝与人工裂缝构成的复杂缝网[12];此外,大多数研究中的优化对象均为客观地质参数[13-14],缺乏针对人为可控参数的优化研究。针对这些问题,基于非结构化网格技术,建立能够显性刻画体积压裂复杂缝网的离散裂缝数值模拟模型,并对体积压裂水平井可控参数进行优化研究,以期为致密油藏体积压裂水平井造缝设计提供依据。
1 离散裂缝模型数值模拟技术目前,针对复杂缝网的模拟方法主要有局部网格加密法(LGR)、Warrant-Root模型和离散裂缝模型(DFM) [15-17]。LGR是一种基于笛卡尔网格的单介质模拟方法,虽然该方法能够用较细网格表征真实裂缝尺寸,但其只能够模拟沿网格x,y,z方向的垂直裂缝,而无法模拟任意方向、任意倾角的裂缝,且其网格数量大,计算耗时长,故不能很好地适用于体积压裂产生的复杂缝网系统;Warrant-Root模型引入双重介质概念,将裂缝型储层简化为一个正交连接的“糖块状”基质-裂缝系统,裂缝连续分布于立方体基质块之间,这种连续性等效假设与实际裂缝的离散性质相矛盾,因而该模型通常只适用于分布较均匀、连通性较好的裂缝的模拟,对于数量较少、横跨区域较广,但对流动有决定性作用的裂缝的模拟则非常不适应;相比于前2种方法,DFM方法使用更为灵活的非结构化网格分别单独表示基质和裂缝,能够用较少的网格对裂缝实际几何特征和分布形态进行完整、显性的描述,能够适应和表征各种物面边界以及各种形态复杂的裂缝系统(图 1),因此,被认为是一种高效、准确的复杂缝网模拟新方法。
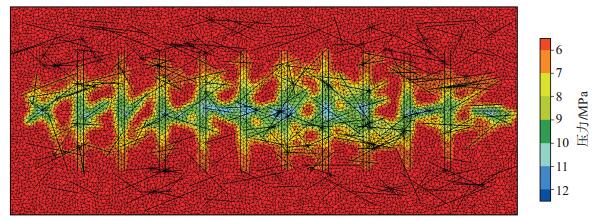
|
下载eps/tif图 图 1 基于DFM模拟的压力场 Fig. 1 Pressure distribution simulated by DFM |
采用基于Delaunay算法的三棱柱网格剖分方法[18]对三维模拟区域进行剖分[图 2(a)]。相比于PEBI等非结构化网格[19],三棱柱网格更具灵活性及剖分的稳定性,适用于各种复杂离散裂缝系统的网格剖分,且具备分层描述的功能[图 2 (b)]。
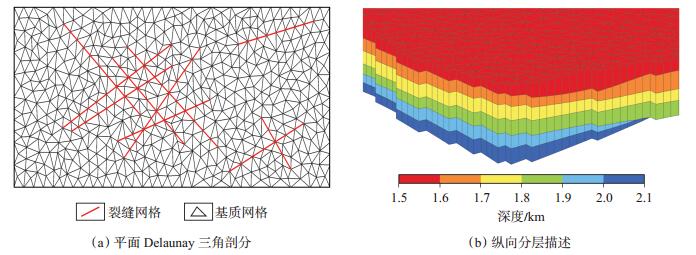
|
下载eps/tif图 图 2 三棱柱网格剖分示意图 Fig. 2 Mesh generation diagram of triangular prism |
与常规储层相比,致密储层岩石的弹塑性变化及流体密度变化对渗流的影响更大,因此必须考虑岩石和流体的压缩性质。由达西定律和质量守恒定律可知,描述三相可压缩流体的连续方程为
| $ \frac{\partial }{{\partial t}}\left( {\varphi {S_t}{\rho _1}} \right) = \nabla \cdot \left( {\frac{{{\rho _1}k{k_{{\text{r}}, {\text{l}}}}}}{{{\mu _\text{l}}}}} \right) + q $ | (1) |
| $ {S_{\text{w}}} + {S_{\text{o}}} + {S_{\text{g}}} = 1 $ | (2) |
| $ {p_{\text{o}}}-{p_{\text{w}}} = {p_{\text{c}}}\left( {{S_{\text{w}}}} \right) $ | (3) |
式(1)~ (3)中:φ为孔隙度,%;S1为相流体的饱和度,%;ρl为相流体的密度,kg/m3;t为时间,s;k为渗透率,10-6 D;kr,l为单相相对渗透率,%;μl为相流体的黏度,Pa·s;p为压力,Pa;q为流量项,kg/(m3·s);Sw,So,Sg分别为水相、油相、气相饱和度,%;po,pw分别为油相、水相压力,Pa;pc为毛管压力,Pa。
描述岩石和流体性质随压力变化的数学模型为
| $ \varphi = {\varphi _0}{{\text{e}}^{{c_\varphi }\left( {p-{p_0}} \right)}} $ | (4) |
| $ k = {k_0}{{\text{e}}^{{c_k}\left( {p-{p_0}} \right)}} $ | (5) |
| $ \rho = {\rho _0}{{\text{e}}^{{c_p}\left( {p-{p_0}} \right)}} $ | (6) |
式(4)~ (6)中:p0为参考压力,Pa;φ0为参考压力下的孔隙度,%;k0为参考压力下的渗透率,10-6 D;ρ0为参考压力下的流体密度,kg/m3;cφ,ck,cρ分别为孔隙度、渗透率及流体密度随压力的变化系数。
2.3 传导率计算模型在油气藏数值模拟过程中,传导率计算是描述网格间流体交换的重要步骤。任意形状的相邻网格传导率的质量传输方程为
| $ {Q_{{\text{l}}, ij}} = {T_{ij}}\frac{{{\rho _{\text{l}}}{k_{{\text{r}}, {\text{l}}}}}}{{{\mu _{\text{l}}}}}\left( {{p_{{\text{l}}, i}}-{p_{{\text{l}}, j}}} \right) $ | (7) |
式中:Ql, ij为网格i与j的传质速率,kg/s;Tij为网格i和j之间的传导率,m3;pl,i和pl,j分别为网格i和j的相压力,Pa。
由于非结构网格的控制体形状多样,相邻2个网格之间难以恒定正交,采用基于控制体积原理的两点流近似方法[20]及基尔霍夫定律的星角变换方法,可推导出不同介质之间传导率的计算公式:
(1) 基质-基质的传导率
| $ {T_{ij}} = \frac{{{\alpha _i}{\alpha _j}}}{{{\alpha _i} + {\alpha _j}}} $ | (8) |
| $ \alpha = \frac{{Ak}}{D}\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{f}} $ | (9) |
(2) 基质-裂缝的传导率
| $ {T_{m-f}} = \frac{{{\alpha _m}{\alpha _f}}}{{{\alpha _m} + {\alpha _f}}} $ | (10) |
| $ {\alpha _m} = \frac{{Ak}}{D}\mathit{\boldsymbol{n}} \cdot \mathit{\boldsymbol{f}} $ | (11) |
| $ {\alpha _f} = \frac{{Ak}}{D} $ | (12) |
(3) 裂缝-裂缝的传导率
| $ {T_{ij}} = \frac{{{\alpha _i}{\alpha _j}}}{{\sum\nolimits_{k = 1}^N {{\alpha _k}} }} $ | (13) |
| $ \alpha = \frac{{Ak}}{D} $ | (14) |
式(8) ~ (14)中:α为网格半传导率,m3;A为网格的交面面积,m2;D为网格中心点到交面中心点的距离,m;k为网格的渗透率,10-6 D;n为交面指向网格的单位法向量;f为交面指向网格中心点的单位法向量;αm,αf分别为基质网格和裂缝网格的半传导率,m3,N为相交的裂缝总数,个。
介质与井筒间的流体交换借助井指数来描述,本文采用Peaceman模型[21]计算井指数。
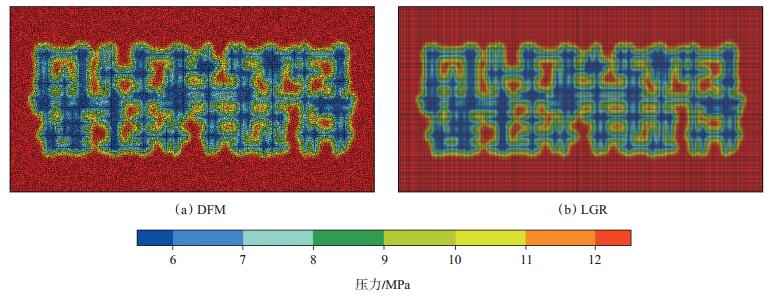
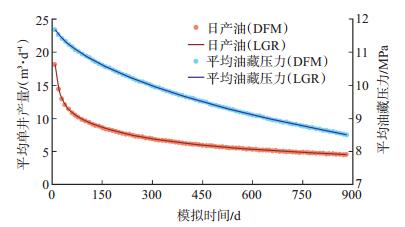
2.4 模型验证 2.4.1 商业数值模拟软件验证在本文离散裂缝模型(DFM)应用前,设计了一组相互垂直的多尺度随机裂缝网络,利用商业模拟器Eclipse对其进行验证。在Eclipse中采用局部网格加密法(LGR)来表征裂缝,其他模拟参数与本文模型保持一致。对比模拟结果表明,在同一模拟时间2种模型计算的压力分布具有较好的一致性(图 3),平均单井日产量曲线和平均油藏压力曲线也均高度吻合(图 4),证明本文模型具有较高的可靠性。
|
下载eps/tif图 图 3 2种模型压力分布对比 Fig. 3 Pressure field comparison of two models |
|
下载eps/tif图 图 4 2种模型生产动态对比 Fig. 4 Production performance comparison of two models |
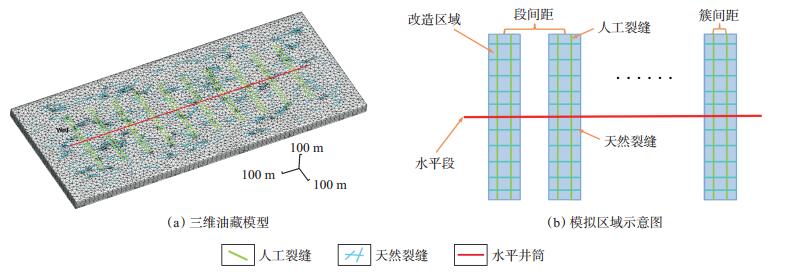
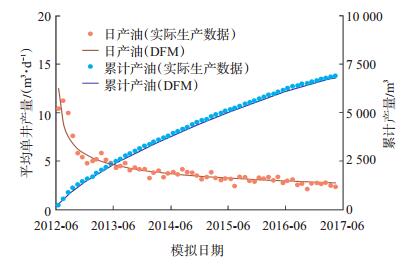
QP-49 H是长庆油田某致密储层的一口10段2簇的体积压裂水平井(图 5),水平段长度为1 495 m,原始地层压力为11.9 MPa,初始含油饱和度为57%,基质平均孔隙度为10%,基质平均渗透率为0.11 mD,岩石压缩系数为8.43×10-5 MPa-1,地层原油黏度为1.03 mPa·s,地层原油密度为0.85 g/cm3,原油体积系数为1.34,原始溶解气油比为70 m3/m3。该井于2012年6月10日投产,截至2017年6月1日累计产油6 876.04 m3。从模拟得到的该井生产动态曲线与实际生产数据对比(图 6)可以看出,模拟结果与实际数据吻合度高,进一步说明了本文模型具有较高的可靠性。
|
下载eps/tif图 图 5 体积压裂水平井模拟模型 Fig. 5 Simulation model of volume fracturing horizontal well |
|
下载eps/tif图 图 6 QP-49 H井实际生产动态与DFM模拟结果对比 Fig. 6 Production performance comparison of DFM and measured values of well QP-49 H |
体积压裂水平井增产效果的影响因素包括客观因素和人为因素,前者是来自储层自身的、影响体积压裂水平井开发效果的地质因素,包括储层的孔渗性、天然裂缝发育程度等,后者主要是指不同的造缝参数设计或开发技术政策方面的因素,包括水平井方位、布缝方式、改造体积、段间距和簇间距等设计,以及压裂裂缝导流能力等。人为因素是开发生产中的可控因素,但也受客观因素的制约,体现在造缝参数应根据不同的地质条件而进行优化设计。
基于本文DFM数值模拟模型以及矿场实际参数,对以下5个与体积压裂设计相关的参数进行了模拟优化。
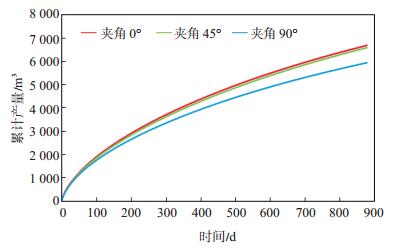
3.1 水平井方位在进行水平井方位设计时,需要考虑裂缝方向,只有当水平井方向、天然裂缝方向和人工裂缝方向三者相匹配时,才能获得最大产能。设计时考虑水平井与天然裂缝夹角分别为0°,45°,90°等3种情形(图 7)。由于主压裂裂缝一般垂直于水平井,当水平井平行于天然裂缝时,压裂裂缝与天然裂缝垂直并相互沟通,开发效果最好;当水平井与天然裂缝垂直时,人工裂缝与天然裂缝平行无沟通,开发效果最差;当水平井与天然裂缝夹角呈45°时,开发效果次于水平井与天然裂缝平行的情况,这是由于后者更有利于裂缝相互交错而形成更大的缝网面积。
|
下载eps/tif图 图 7 水平井方位对累计产量的影响 Fig. 7 Influence of the orientation of horizontal well on cumulative production |
不同长度的布缝组合对水平井产能具有一定影响[22]。设计4种模拟方案(表 1),除每段的裂缝半长从左至右按表 1设计外,每种布缝方式都将6段2簇的压裂裂缝等间距布置于水平井上,且总裂缝长度相同,均为4 800 m。
|
|
下载CSV 表 1 水平井布缝方案 Table 1 Simulation types of fracture arrangement |
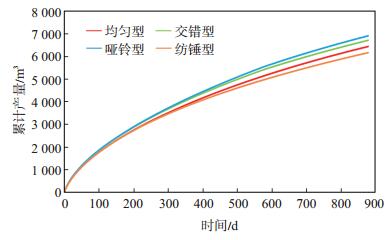
从图 8可知,虽然每种布缝方式总裂缝长度相同,但累计产量却有明显差异,按累计产量由大到小排序,依次为哑铃型、交错型、均匀型、纺锤型;生产初期4种布缝方式的产量相差不大,中后期差异逐步增大,这是由于初期产量受裂缝与储层接触面积控制,在裂缝高度相等的情况下,产量相差不大,而中后期由于泄油面积的重叠,内部裂缝相互干扰,外侧裂缝的缝长会影响产量。
|
下载eps/tif图 图 8 布缝方式对累计产量的影响 Fig. 8 Influence of fracture arrangement on cumulative production |
为了避免体积压裂裂缝段间相互干扰,需要对段间距进行优化设计。模拟发现,不同的人工裂缝导流能力和基质渗透率都会对段间距的设计产生影响。
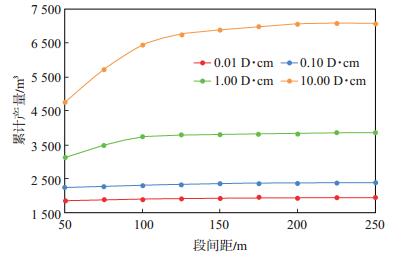
设计人工裂缝导流能力分别为0.01 D·cm,0.10 D·cm,1.00 D·cm,10.00 D·cm的情况,研究累计产量与段间距的关系。从图 9可知,当人工裂缝导流能力较差时,段间距对累计产量影响不大,但随着人工裂缝导流能力的增强,段间距对累计产量的影响逐渐增大,这是由于人工裂缝的导流能力越强,其控制的泄油面积越大,相邻段间相互干扰的情况就越明显;累计产量随着段间距的增大而增加,但增加的幅度由大变小,这是由于当段间距较小时,相邻两段的泄油面积重叠部分较大,储量动用程度低,随着段间距增大,相邻两段的泄油面积重叠部分变小,总泄油面积变大,表现为累计产量快速增加,且裂缝导流能力越强,增加的幅度越大,而随着段间距持续增大,相互干扰作用不断减弱,累计产量增加的幅度也变小,最后趋于不变。
|
下载eps/tif图 图 9 不同人工裂缝导流能力下累计产量与段间距的关系 Fig. 9 Relationship between stage spacing and cumulative production with different hydraulic fracture conductivity |
因此,在设计最优段间距时,应保证每段之间的距离大于相邻两段的泄油半径之和。最优段间距与人工裂缝导流能力有关,可根据数值模拟计算得到。对于导流能力较差的人工裂缝,可设置多段小段间距,以保证储量的动用和一定的经济效益;对于导流能力较好的人工裂缝,则可设置较大的段间距,以节省施工成本。
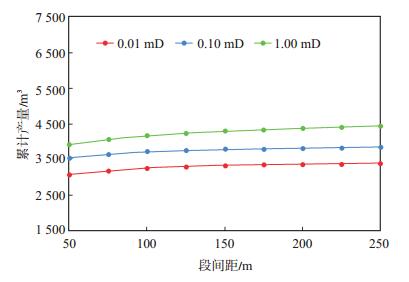
同样,设计基质渗透率分别为0.01 mD,0.10 mD,1.00 mD的情况,研究累计产量与段间距的关系。对比图 9和图 10可知,在不同基质渗透率情况下累计产量与段间距关系曲线的趋势基本不变,可见基质渗透率对段间距优选的影响很小,而人工裂缝导流能力是影响段间距优选的主要因素;单看某一段间距情况下基质渗透率对累计产量的影响发现,对致密储层来说,基质渗透率的增大对产量增加的影响较小,而随人工裂缝导流能力的增强,累计产量的增加十分显著,这说明裂缝是致密储层的主要渗流通道和增产的关键影响因素,基质渗透率对裂缝的供油能力虽有一定影响,但这种影响在致密储层中不明显。
|
下载eps/tif图 图 10 不同基质渗透率下累计产量与段间距的关系 Fig. 10 Relationship between stage spacing and cumulative production with different matrix permeability |
分段多簇射孔技术是储层体积改造方法之一[23],簇内裂缝的相互干扰是在设计簇间距时需要考虑的。除了人工裂缝导流能力和基质渗透率之外,与人工裂缝相互沟通交错的天然裂缝也对簇间距的设计有影响。设计了不同模拟参数,即天然裂缝间距(10~50 m)、天然裂缝渗透率(0.1~100.0 D)、人工裂缝导流能力(0.01~10.00 D·cm)及基质渗透率(0.01~1.00 mD),研究累计产量与簇间距的关系(图 11)。
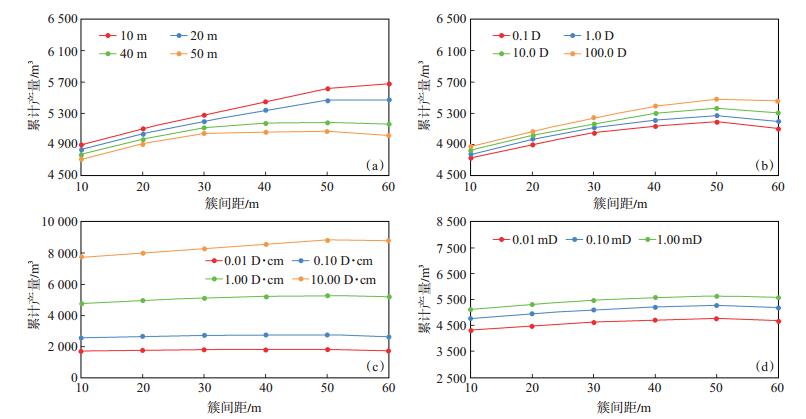
|
下载eps/tif图 图 11 不同天然裂缝间距(a)、天然裂缝渗透率(b)、人工裂缝导流能力(c)、基质渗透率(d)下累计产量与簇间距的关系 Fig. 11 Relationship between cluster spacing and cumulative production under different fracture spacing(a), fracture permeability(b), hydraulic fracture flow conductivity(c)and matrix permeability(d) |
从图 11(a)~(d)可知,当簇间距从10 m增大到50 m时,累计产量都有随着簇间距增大而增加的趋势。这是由于随着簇间距增大,簇内缝干扰情况减弱,且改造区域面积和总泄油面积均增大,产量增加;产量增加的幅度有所差异,即天然裂缝间距越小[图 11 (a)]、渗透率越大[图 11 (b)]及人工缝导流能力越强[图 11(c)],累计产量增加的幅度均越大,而基质渗透率对累计产量增加幅度的影响较小[图 11(d)],这也进一步说明了裂缝是控制产量的主导因素;当簇间距大于50 m时,累计产量均开始下降,这是由于簇间距比天然裂缝平均缝长50 m大,此时人工裂缝和天然裂缝沟通的情况变少,因此产量降低。
从图 11(a)~(d)中固定簇间距对比可知,天然裂缝间距越小,裂缝越发育,提供的油气渗流通道更多,累计产量也越大;天然裂缝渗透率越高,人工裂缝导流能力越强,相同时间内的泄油面积越大,累计产量也越大;基质渗透率越大,基质的供油速度越快,累计产量也越大。
综上所述,当天然裂缝间距小、渗透率高、人工裂缝导流能力强、基质渗透率大的情况下进行簇间距设计时,应以获得最大缝网面积为目标,尽可能使簇间距大,但不要超过天然裂缝的平均缝长;在造缝时,应在施工条件允许的情况下,使人工裂缝导流能力最大。
3.5 改造体积通常情况下改造体积越大,泄油体积越大,产能越高[24-25]。为了研究在相同的改造体积情况下,如何对不同参数进行优化,设计了4种模拟方案(表 2),各种方案中每段的改造体积及其他油藏参数均相同。图 12为模拟结果。
|
|
下载CSV 表 2 模拟方案参数设计 Table 2 Designed simulation schemes |
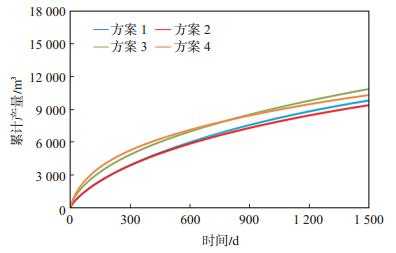
|
下载eps/tif图 图 12 不同方案的累计产量对比 Fig. 12 Comparison curves of cumulative production of different schemes |
结合表 2和图 12分析可知:对比方案1和方案2,当段内簇数相同时,裂缝半长越大,产能越高,即改造体积一定时,细长形状的改造区域比短粗形状的改造区域开发效果更好;对比方案2和方案3,当改造区域形状相同时,段内簇数越大,初期的累计产量越高;分别对比方案1和方案3、方案2和方案4,当改造体积相同时,裂缝半长较小的3簇、4簇压裂开发效果优于裂缝半长较长的2簇压裂,这是因为3簇、4簇的压裂裂缝被天然裂缝切割成更细的网状缝,大大缩短了泄油面积内的点到裂缝的距离,因此,当工艺难以达到增加人工裂缝长度时,可依靠增加压裂簇数进而增加网状缝来提高累计产量;对比方案3和方案4,当开发时间小于800 d时,4簇压裂开发效果优于3簇压裂,超过800 d后,3簇压裂开发效果反而优于4簇压裂,这说明段内簇数和网状缝也不是越多越好,还取决于开采时间的长短。
4 结论(1) 本文建立的非结构化网格的离散裂缝模型能够很好地对裂缝的实际尺寸和分布形态进行完整和显性的描述,并能较好地对体积压裂复杂缝网进行刻画,借助Eclipse软件及矿场实际井资料验证了该模型的可靠性,可推广应用于其他裂缝型储层的模拟。
(2) 在水平井方位设计时,须综合考虑水平井、人工裂缝和天然裂缝三者方向的相互匹配性,当水平井方向和天然裂缝方向平行时开发效果最好。
(3) 不同的布缝方式对水平井产量有一定的影响,按累计产量由大到小排序依次为哑铃型、交错型、均匀型、纺锤型。
(4) 人工裂缝导流能力是影响段间距优选的主要因素,对于导流能力较强的人工裂缝,可设置较大的段间距以节省施工成本,反之,可采用多段小段间距的人工裂缝达到相同开发效果。簇间距设计时,应使簇间距小于天然裂缝平均缝长以获得更多的沟通缝网,同时尽可能使簇间距大以获得最大改造体积。
(5) 段内簇数相同时,细长形状的改造区域比短粗形状的改造区域开发效果更好,当设计的压裂裂缝长度达不到理想值时,可以通过增加压裂簇数提高开发效果,但最优簇数还要取决于开采时间的长短。
| [1] |
赵政璋, 杜金虎, 邹才能, 等. 致密油气. 北京: 石油工业出版社, 2012, 1-42. ZHAO Z Z, DU J H, ZOU C N, et al. Tight oil and gas. Beijing: Petroleum Industry Press, 2012, 1-42. |
| [2] |
杨华, 李士祥, 刘显阳. 鄂尔多斯盆地致密油、页岩油特征及资源潜力. 石油学报, 2013, 34(1): 1-11. YANG H, LI S X, LIU X Y. Characteristics and resource prospects of tight oil and shale oil in Ordos Basin. Acta Petrolei Sinica, 2013, 34(1): 1-11. DOI:10.7623/syxb201301001 |
| [3] |
邱振, 李建忠, 吴晓智, 等. 国内外致密油勘探现状、主要地质特征及差异. 岩性油气藏, 2015, 27(4): 119-126. QIU Z, LI J Z, WU X Z, et al. Exploration status, main geologic characteristics and their differences of tight oil between America and China. Lithologic Reservoirs, 2015, 27(4): 119-126. |
| [4] |
付金华, 喻建, 徐黎明, 等. 鄂尔多斯盆地致密油勘探开发新进展及规模富集可开发主控因素. 中国石油勘探, 2015, 20(5): 9-19. FU J H, YU J, XU L M, et al. New progress in exploration and development of tight oil in Ordos Basin and main controlling factors of large-scale enrichment and exploitable capacity. China Petroleum Exploration, 2015, 20(5): 9-19. |
| [5] |
贾承造, 邹才能, 李建忠, 等. 中国致密油评价标准、主要类型、基本特征及资源前景. 石油学报, 2012, 33(3): 343-350. JIA C Z, ZOU C N, LI J Z, et al. Assessment criteria, main types, basic features and resource prospects of the tight oil in China. Acta Petrolei Sinica, 2012, 33(3): 343-350. DOI:10.7623/syxb201203001 |
| [6] |
王秀娟, 王明磊, 赵爱彬. 鄂尔多斯盆地延长组长7致密油储层微观特征. 岩性油气藏, 2014, 26(3): 79-83. WANG X J, WANG M L, ZHAO A B. Microscopic characteristics of Chang 7 tight sandstone reservoir in Ordos Basin. Lithologic Reservoirs, 2014, 26(3): 79-83. |
| [7] |
李卫成, 叶博, 张艳梅, 等. 致密油水平井体积压裂攻关试验区单井产量主控因素分析. 石油地质与工程, 2016, 30(6): 111-114. LI W C, YE B, ZHANG Y M, et al. The main control factors of single well productivity for the experiment block using horizontal well by volume fracturing in tight oil reservoir. Petroleum Geology and Engineering, 2016, 30(6): 111-114. |
| [8] |
樊建明, 杨子清, 李卫兵, 等. 鄂尔多斯盆地长7致密油水平井体积压裂开发效果评价及认识. 中国石油大学学报(自然科学版), 2015, 39(4): 103-110. FAN J M, YANG Z Q, LI W B, et al. Assessment of fracturing treatment of horizontal wells using SRV technique for Chang-7 tight oil reservoir in Ordos Basin. Journal of China University of Petroleum(Edition of Natural Science), 2015, 39(4): 103-110. |
| [9] |
韩婧婧, 刘建, 武龙. 鄂尔多斯盆地长6致密砂岩油藏压裂技术研究. 岩性油气藏, 2017, 29(1): 130-134. HAN J J, LIU J, WU L. Investigation on fracturing technology of Chang 6 tight sandstone reservoir in Ordos Basin. Lithologic Reservoirs, 2017, 29(1): 130-134. |
| [10] |
张娅妮, 马新仿. 页岩气体积压裂数值模拟研究. 天然气与石油, 2015, 33(1): 54-58. ZHANG Y N, MA X F. Numerical simulation study on shale gas volume fracturing. Natural Gas and Oil, 2015, 33(1): 54-58. |
| [11] |
孟展, 杨胜来, 王璐, 等. 合水长6致密油体积压裂水平井产能影响因素分析. 非常规油气, 2016, 3(5): 127-133. MENG Z, YANG S L, WANG L, et al. Analysis of influence factors on horizontal well productivity by volume fracturing in Heshui Chang 6 tight oil reservoir. Unconventional Oil and Gas, 2016, 3(5): 127-133. |
| [12] |
潘有军, 荆文波, 徐赢, 等. 火山岩油藏水平井体积压裂产能预测研究. 岩性油气藏, 2018, 30(3): 159-164. PAN Y J, JING W B, XU Y, et al. Productivity prediction of horizontal wells by volume fracturing in volcanic reservoirs. Lithologic Reservoirs, 2018, 30(3): 159-164. |
| [13] |
孙兵, 刘立峰, 丁江辉. 致密油水平井产能主控地质因素研究. 特种油气藏, 2017, 24(2): 115-119. SUN B, LIU L F, DING J H. Study of the main geological control factors on horizontal well productivity in tight oil reservoir. Special Oil and Gas Reservoirs, 2017, 24(2): 115-119. |
| [14] |
闵春佳, 卢双舫, 唐明明, 等. 致密油储层水平井压裂参数优化模拟. 断块油气田, 2015, 22(6): 794-797. MIN C J, LU S F, TANG M M, et al. Hydro-fracturing parameter optimization and simulation of horizontal well in tight oil reservoir. Fault-Block Oil and Gas Field, 2015, 22(6): 794-797. |
| [15] |
胡嘉, 姚猛. 页岩气水平井多段压裂产能影响因素数值模拟研究. 石油化工应用, 2013, 32(5): 34-39. HU J, YAO M. Multiple fracturing of horizontal well in shale gas productivity factors numerical simulation researching. Petrochemical Industry Application, 2013, 32(5): 34-39. |
| [16] |
WARREN J E, ROOT P J. The behavior of naturally fractured reservoirs. SPE Journal, 1963, 3(3): 245-255. DOI:10.2118/426-PA |
| [17] |
KARIMI-FARD M, FIROOZABADI A. Numerical simulation of water injection in fractured media using the discrete-fracture model and the Galerkin method. SPE Reservoir Evaluation & Engineering, 2003, 6(2): 117-126. |
| [18] |
ZHANG Y B, GONG B, LI J C, et al. Discrete fracture modeling of 3 D heterogeneous enhanced coalbed methane recovery with prismatic meshing. Energies, 2015, 8(6): 6153-6176. DOI:10.3390/en8066153 |
| [19] |
彭晖, 刘玉章, 冉启全, 等. 致密油储层水平井产能影响因素研究. 天然气地球科学, 2014, 25(5): 771-777. PENG H, LIU Y Z, RAN Q Q, et al. Study on the horizontal well production in tight oil reservoirs. Natural Gas Geoscience, 2014, 25(5): 771-777. |
| [20] |
KARIMI-FARD M, DURLOFSKY L J, AZIZ K. An efficient discrete-fracture model applicable for general-purpose reservoir simulators. SPE 88812, 2004. |
| [21] |
PEACEMAN D W. Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability. SPE Journal, 1983, 23(3): 531-543. DOI:10.2118/10528-PA |
| [22] |
YU W, LUO Z, JAVADPOUR F, et al. Sensitivity analysis of hydraulic fracture geometry in shale gas reservoirs. Journal of Petroleum Science and Engineering, 2014, 113(1): 1-7. |
| [23] |
刘建伟, 张佩玉, 廖天彬, 等. 马58 H致密油藏水平井分段多簇射孔压裂技术. 石油钻采工艺, 2015, 37(3): 88-92. LIU J W, ZHANG P Y, LIAO T B, et al. Staged multi-cluster perforation fracturing technology for horizontal well Ma-58 H in tight reservoir. Oil Drilling and Production Technology, 2015, 37(3): 88-92. |
| [24] |
刘卫东, 张国栋, 白志峰, 等. 致密油藏水平井多级压裂储层改造体积评价. 新疆石油地质, 2015, 36(2): 199-203. LIU W D, ZHANG G D, BAI Z F, et al. Evaluation of stimulated reservoir volume(SRV) in tight oil reservoirs by horizontal well multistage fracturing process. Xinjiang Petroleum Geology, 2015, 36(2): 199-203. |
| [25] |
蒋廷学, 王海涛, 卞晓冰, 等. 水平井体积压裂技术研究与应用. 岩性油气藏, 2018, 30(3): 1-11. JIANG T X, WANG H T, BIAN X B, et al. Volume fracturing technology for horizontal well and its application. Lithologic Reservoirs, 2018, 30(3): 1-11. |
 2018, Vol. 30
2018, Vol. 30