2. 西南石油大学 地球科学与技术学院, 成都 610500;
3. 电子科技大学 资源与环境学院, 成都 610054
2. School of Geoscience and Technology, Southwest Petroleum University, Chengdu 610500, China;
3. School of Resources and Environment, University of Electronic Science and Technology of China, Chengdu 610054, China
随着油气勘探和开发工作的不断深入,层序地层界面的定量划分越来越受到人们的重视。传统的层序地层划分及对比主要是在观察、分析野外露头和岩心的基础上,结合地震与测井资料进行的。其中,测井数据包含有丰富的地质信息,具有分辨率高,连续性好等特征[1]。自20世纪80年代以来,在利用岩性无法进行层序地层划分的情况下,通常通过分析测井曲线来识别层序地层界面。郑小武等[2]主要利用自然电位(SP)和自然伽马(GR)曲线进行岩性突变点的识别,从而识别出地层层序界面,以及通过SP和GR曲线的形态,即测井相划分方法来描述层序地层的旋回性,从而划分出对应的层序地层单元。
时频分析技术的发展进一步提高了利用测井数据进行层序地层划分的精度,李江涛等[3]提出了基于小波变换的测井数据地层层序对比与划分方法,利用小波变换多尺度、多分辨率的特性进行层序划分[4-6],但小波窗会影响地层层序的识别精度[7]。徐敬领等[8]率先将经验模态分解(Empirical Mode Decomposition,EMD)方法运用于层序地层划分及对比,利用EMD将测井数据分解成相对独立的频率分量,通过各分量形态及幅值特征识别不同周期的沉积旋回[9-10],获得了较好的应用效果。
经验模态分解是由Huang等[11]提出的一种高时频分辨率信号分析方法。区别于小波及S变换等传统的时频分析方法,EMD能自适应地将原信号分解成若干平稳的信号分量,称之为本征模态函数(Intrinsic Mode Function,IMF),从而将原信号中真实存在的不同尺度的波动或趋势逐级提取出来,不受窗函数的约束[12-13]。EMD已经在地震、雷达、语音信号处理以及图像分析等领域广泛应用[14]。EMD的这些特性为测井数据的非线性本征分解和地质分析提供了有效的信号处理手段,然而其存在模态混叠现象,当信号的频率分布比较密集时,EMD出来的IMF失真,从而影响频谱分析的结果[15]。
总体经验模态分解(Ensemble Empirical Mode Decomposition,EEMD)方法是对EMD的进一步完善,是一种噪声辅助信号分析方法,该方法兼具EMD方法的优点,同时改善了EMD的模态混叠问题,具有更高的时频分辨率,其原理是利用高斯白噪具有频率均匀分布的统计特性,通过向信号中添加高斯白噪,使得信号在不同的尺度上具有更好的连续性。最后对多次EMD得到的IMF分量进行整体平均,从而改善模态混叠[16]。以东营凹陷沙三段为例,利用EEMD方法分解该区GR数据获得不同尺度下的IMF分量,通过相关分析方法优选与原始GR数据相关程度高的分量,根据其尺度大小,分别进行短期、中期以及长期旋回的划分,以期为高分辨率层序地层划分提供新思路。
1 总体经验模态分解(EEMD)原理及层序划分方法 1.1 EEMD原理EMD假设任何信号都是由有限个本征模态函数组成[17],通过EMD将信号分解成更易分析的若干本征模态函数和一个残差的集合,具有完全的自适应性,但EMD存在模态混叠问题。模态混叠是指当信号的时间尺度存在跳跃性变化时,信号在EMD后会在同一个本征模态分量中同时出现不同时间尺度的特征成分。
EEMD方法是对EMD方法的改进,通过多次向原始信号加入不同的高斯白噪,然后对复合信号进行多次EMD,得到多组IMF,并求平均值作为最终的IMF。EEMD具体方法如下:
(1)在原始信号中多次加入等长度不等幅值的高斯白噪wi(t),得到新的待分解信号Xi(t):
| $ {X_i}\left( t \right) = x\left( t \right) + {w_i}\left( t \right) $ | (1) |
式中:i为添加高斯白噪的次数;Xi(t)为第i次加入高斯白噪后的信号;wi(t)为第i次添加的高斯白噪;x(t)原始的输入信号。
(2)对复合信号进行N次EMD,并分别对N次分解得到的IMF求平均值,作为新的IMF:
| $ {\rm{IM}}{{\rm{F}}_j}\left( t \right) = \frac{1}{N}\sum\limits_{i = 1}^N {{\rm{IM}}{{\rm{F}}_{i, j}}} \left( t \right) $ | (2) |
式中:IMFi, j为第i次添加高斯白噪后,再通过EMD得到的第j个IMF分量;IMFj为IMFi, j的总体平均值;N为分解次数。
(3)复合信号经过N次分解得到的N组残差求平均值作为新的残差R:
| $ R = \frac{1}{N}\sum\limits_{i = 1}^N {{R_i}} $ | (3) |
式中:Ri为第i次分解的残差;R为Ri的总体平均值。
添加的高斯白噪遵循下述统计规律
| $ E = \frac{a}{{\sqrt N }}或\ln E + 0.5a\ln N = 0 $ | (4) |
式中:E为原信号标准差,即输入信号与IMF分量重构结果的偏离;a为高斯白噪的幅值[18]。
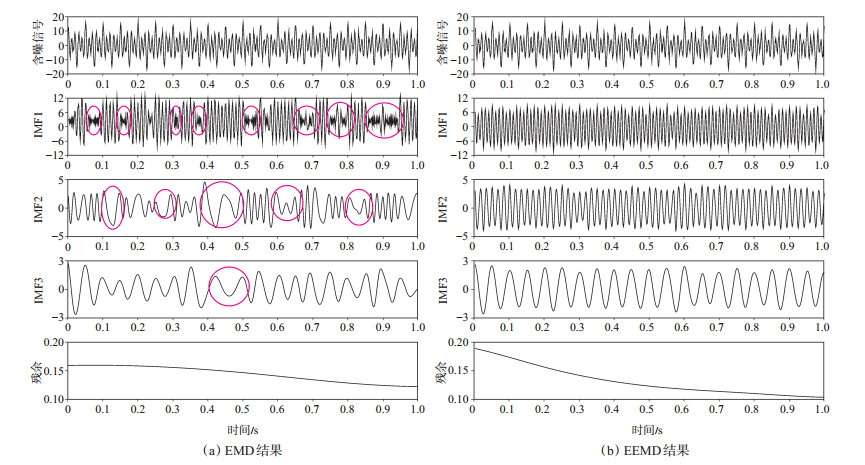
对仿真信号x(t) = 2 cos(40 π t) + 5 cos(120 π t) + 8 cos(200 π t)分别进行EMD和EEMD,仿真信号包含20 Hz,60 Hz和100 Hz这3种频率成分。考虑在实际的测井施工中,噪声的干扰是不可避免的,因此向原始信号中添加强度为0.5 dB的高斯白噪。加入噪声后的仿真信号的EMD及EEMD结果如图 1所示。
|
下载eps/tif图 图 1 含噪信号EMD与EEMD结果对比 Fig. 1 Comparison of EMD and EEMD results of noisy signals |
图 1(a)为EMD结果,原始信号中的20 Hz,60 Hz和100 Hz频率成分分别分布在IMF1,IMF2以及IMF3中,可以看出每个分量中都包含多种频率成分(红色圆圈区域)。图 1(b)为EEMD结果,20 Hz,60 Hz和100 Hz的频率成分分别分布在IMF1,IMF2以及IMF3中,且EEMD后的各频率分量较纯净,没有出现EMD中的频率混杂的现象。
EEMD方法包含了EMD方法的优点,同时基于噪声辅助信号的思想,在分解过程中向原始信号添加高斯白噪,补充了原始信号中一些缺失的成分,有效地解决了EMD的模态混叠问题,获得了更好的分解效果。
1.2 层序划分方法测井数据作为一定时间序列内各种沉积事件的记录,可以准确地反映地层的周期性和旋回性等沉积特征。测井曲线纵向分辨率较高,能够满足划分地层单元的需要。层序界面的岩性和沉积特征往往存在较大的差异,在测井曲线上就体现为波动幅度以及频率的差异[19]。刘腾等[20]提出测井曲线层序地层划分方法仅仅考虑了曲线波动幅度变化对层序界面的指示,通过曲线波动幅度变化异常确定层序界面的具体位置存在较大困难。测井数据频率的突变点往往表示地层岩性以及粒度发生变化,对层序边界处的频率突变反映比较灵敏。利用EEMD将其分解为不同的频率范围,在各个相对独立的分量上识别突变点或突变区域,得到与之对应的沉积转换面,进而指导层序地层的划分。
以东营凹陷牛庄洼陷沙三段为例进行层序地层划分研究,该段地层主要为深色泥岩夹砂岩和页岩。在众多测井曲线中,GR曲线能够充分反映沉积物粒度、分选以及泥质含量,能够表征地层的旋回性以及沉积环境的变化。因此,选用GR数据进行基于EEMD的层序划分研究,具体方法如下:
(1)选取GR数据进行EEMD,得到若干从高频到低频分布的不同频带范围的IMF分量,其中低阶高频IMF分量包含EEMD算法添加的高斯白噪以及测量仪器产生的高频的噪声,因此不予考虑。
(2)利用Hilbert变换计算各IMF分量对应的瞬时频率,得到各IMF分量的Hilbert谱,并结合下文的旋回模型建立起IMF分量频率响应与不同旋回模型的对应关系。
(3)依据不同周期沉积旋回与相应频带内的IMF分量的对应关系进行层序划分及对比。高频IMF分量波动周期短,对应频率高,作为短周期沉积旋回的划分依据;中频IMF分量较高频分量波动周期稍长,频率较低,用于中等周期的沉积旋回的划分;低频IMF分量波动周期长,频率低,适用于长周期层序划分。
2 旋回模型及其EEMD频率响应特征分析沉积旋回在地层剖面上表现为若干岩性以及岩相相似的岩石周期性重复,其实际上是岩石岩性、结构和构造等的体现。运用一个非平稳信号来模拟正、反旋回简单的复合旋回,运用EEMD对原始信号进行分解,得到不同沉积旋回类别的EEMD响应模型。原始信号的表达式为
| $ x\left( t \right) = 6\;t\;\sin \left( {40{\rm{ \mathit{ π} }}{t^{\frac{3}{2}}}} \right), t \in \left[ {0, 1} \right] $ | (5) |
由图 2(a)~(c)可以看出原始信号的S变换和小波变换时频谱上均表现为能量团。S变换在仿真信号终止位置,如在时间0 s处会出现能量异常[图 2(b)],即说明在信号突变或者间断处,S变换时频谱会产生异常能量团信息,从而干扰研究人员对层序突变界面的识别。相对于S变换,小波变换受到小波基函数的影响,在时间域上会出现能量团间断[图 2(c)],需要研究人员自行按照能量团强弱程度判断层序样式。同时,S变换与小波变换受海森伯格测不准定律约束[21],当保持时间域分辨率较高时,频率域上能量团横向分布范围更宽,即频率域分辨率降低,从而较难识别混合频率信息较多的测井信号的频率分布情况。EEMD方法可以更加直观地反映出频率的变化趋势[图 2(d)]。

|
下载eps/tif图 图 2 原始信号不同时频分析方法效果对比 Fig. 2 Comparison of different time-frequency analysis methods for original signal |
正旋回主要在海平面上升时期形成,随水体深度不断增加,沉积物表现为沿岸的退积,同时也表示了水动力从强变弱,沉积物粒度自下而上从粗粒过渡到细粒,其频率在垂向上表现为自下而上由高变低的趋势。反旋回与正旋回则相反,表示了水动力从弱变强,沉积物粒度从细粒逐渐过渡到粗粒,其频率在垂向上表现为自下而上由低变高的趋势。在不同沉积旋回类型的突变点处往往表现为GR与SP等测井曲线频率的突变。因此,对测井曲线频率突变点位置的识别可作为地层岩性及沉积旋回突变界面的判别依据[22]。
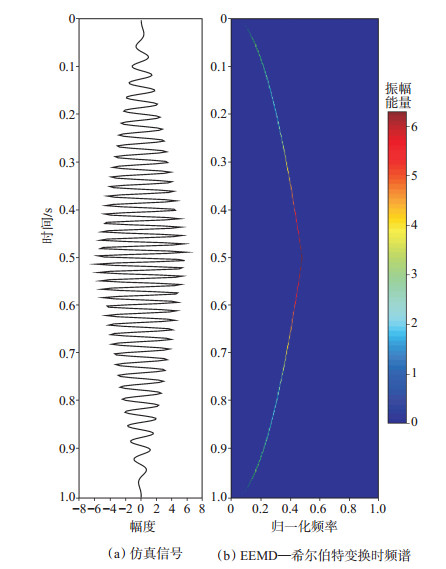
模型一:建立自下而上的反、正旋回组合仿真信号[图 3(a)],其信号频率从下而上由低变高再变低,可以表示岩性由细到粗再到细的沉积过程,对该仿真信号作基于EEMD的希尔伯特时频谱分析[图 3(b)],时频谱可以清晰地表示出沉积旋回的变化,反映出频率转换界面处能量最强,能够清楚地指示出仿真信号的地层转换界面,其时频谱分析与仿真信号所模拟的地质信息吻合。
|
下载eps/tif图 图 3 模型一及其频率响应 Fig. 3 Model Ⅰ and its frequency response |
模型二:同理,建立自下而上的正、反旋回组合仿真信号[图 4(a)],该仿真信号频率从下而上由高变低再变高,仿真信号0.5 s处为频率大小的转换点,其希尔伯特时频谱[图 4(b)]同样能够准确地识别出频率转换点,表明该方法可以清晰地反映出地层转换界面。

|
下载eps/tif图 图 4 模型二及其频率响应 Fig. 4 Model Ⅱ and its frequency response |
本次研究对东营凹陷牛庄洼陷沙三段进行层序地层划分与研究。东营凹陷位于渤海湾盆地东部,属于济阳凹陷中的一个次级构造单元。凹陷内古近系沉积厚度超过5 000 m,主要由湖泊成因的砂岩和泥岩组成[23],其中沙三段主要由深色泥岩组成,同时含有砂岩和页岩,砂岩透镜体发育,主要形成于湖底扇、扇三角洲、三角洲等沉积环境[24]。研究层段(沙三中亚段)主要为一套灰色、深灰色泥岩,夹少量砂岩,盆地边缘地区砂岩发育,体系域类型主要为湖侵域(LTST)和湖退域(LRST)组成[25-26]。以B108井和C117井为例进行GR曲线的EEMD以及层序划分。对各IMF分量与原始GR数据进行相关性分析(表 1),选取相关系数大于0.5的IMF4,IMF5与IMF7分量进行层序划分。图 5是该区B108井的层序划分结果,第2道为GR曲线,第7~9道分别为GR数据通过EEMD得到的第4、第5以及第7分量,第10~12道分别为其对应的Hilbert频率谱。该层段对应的深度为1 500~ 1 850 m,1 672 m处为层序界面,该层序界面对应IMF5和IMF7分量的频率极值点(图 5粉红色椭圆区域)。IMF4和IMF5分量在层序界面上、下明显分为2组不同幅度的波动。IMF7分量则表现为2组相似的波动,其频率自下而上表现为2组由低变高再变低的变化趋势,符合模型一的变化特征,因此可划分成2个层序,自下而上分别对应一个完整的长周期基准面旋回的反、正旋回组合,与岩性剖面的岩性粒度变化趋势吻合。
|
|
下载CSV 表 1 B108井各IMF分量与原始GR数据相关分析结果 Table 1 Analysis results of correlation between IMF components and original GR in well B108 |

|
下载eps/tif图 图 5 B108井层序划分结果 Fig. 5 Sequence division results of well B108 |
图 6是该区C117井的层序划分结果,对各IMF分量与原始测井数据进行相关性分析(表 2),选取相关系数在0.4左右的IMF3,IMF4与IMF6分量进行层序划分。2 860 m处为层序Ⅰ和层序Ⅱ的层序界面(粉色线条所示),其中层序Ⅰ和层序Ⅱ又可细分为湖进域(LTST)和湖退域(LRST)。图 6中2 700~2 787 m井段以及2 862~2 907 m井段均为湖退域,其在IMF3,IMF4以及IMF6分量中均表现为相对强的波动幅度。在频率域,IMF6分量的频率则表现为自下而上由小变大的趋势,表明沉积物粒度下细上粗的特征。2 787~2 862 m井段以及2 907~2 975 m井段均为湖进域,其在IMF3,IMF4与IMF6分量中均表现为相对较小的波动幅度。在IMF6分量的频率则呈现出自下而上由大变小的趋势,表明沉积物粒度下粗上细的特征。层序Ⅰ和层序Ⅱ的分界面对应IMF6分量频率的极大值点,体系域界面分别对应IMF6分量频率的极小值点(图 6粉红色椭圆所示)。

|
下载eps/tif图 图 6 C117井层序划分结果 Fig. 6 Sequence division results of well C117 |
|
|
下载CSV 表 2 C117井各IMF分量与原始GR数据相关分析结果 Table 2 Analysis results of correlation between IMF components and original GR in well C117 |
图 6中第4道为GR曲线的镜像显示,传统层序地层划分的手段多是利用测井曲线的镜像,通过对测井曲线的几何形态和幅值变化的分析来指导层序单元的划分,然而测井曲线镜像往往所表现的旋回特征不明显且曲线形态变化随机性较大,难以通过测井曲线镜像准确地识别地层的旋回特征,而且受人为经验的影响较大,而利用EEMD方法对测井数据进行多尺度分析,将测井数据内相互叠加的不同周期的沉积旋回信息分解成相互独立的频率成分,以不同的尺度展现出来。结合低频分量的概貌信息与高频分量的细节信息,指导层序地层划分。通过测井数据高、低频分量的波动异常以及低频分量频率的突变点和拐点识别地层岩性的突变及层序界面。利用高频分量的波动及频率异常放大层序地层单元,细化沉积旋回类型。
4 结论(1)利用EEMD以及Hilbert变换方法对测井曲线进行处理,将测井信号从一维深度域扩展为二维深度-频率域,可以有效地提取测井曲线信号中隐藏的丰富的地质信息,清晰地展现出测井曲线内不同能量的波动情况,更加准确地反映地层层序特征,有利于沉积旋回及地层层序的研究。
(2)不同频率域的固有模态IMF分量与不同周期的基准面旋回存在对应关系,高频IMF分量对应短周期基准面旋回;中频IMF分量对应中等周期的基准面旋回;低频IMF分量对应长周期基准面旋回;各分量的突变点或突变区域对应相应的沉积转换界面。
(3)EEMD以及Hilbert变换方法在东营凹陷沙三段层序地层划分中取得了较好的应用效果,验证了该方法的有效性和可行性,为层序地层划分及对比研究提供了新思路。
| [1] |
闫建平, 蔡进功, 赵铭海, 等. 测井信息用于层序地层单元划分及对比研究综述. 地层学杂志, 2009, 33(4): 441-450. YAN J P, CAI J G, ZHAO M H, et al. Advances in the study of sequence stratigraphic division and correlation using well log information. Journal of Stratigraphy, 2009, 33(4): 441-450. DOI:10.3969/j.issn.0253-4959.2009.04.013 |
| [2] |
郑小武, 邓宏文, 徐怀大, 等. 测井高分辨率层序地层自动划分技术与应用尝试. 石油与天然气地质, 1999, 20(4): 357-360. ZHENG X W, DENG H W, XU H D, et al. Automatic recognizing technique of log high-resolution sequence stratigraphy and its application. Oil & Gas Geology, 1999, 20(4): 357-360. |
| [3] |
李江涛, 李增学, 余继峰, 等. 基于测井数据小波变换的层序地层对比——以鲁西和济阳地区石炭、二叠系含煤地层为例. 沉积学报, 2005, 23(4): 639-645. LI J T, LI Z X, YU J F, et al. Stratigraphic sequence correlation based on wavelet transform of well logging data:Taking the coal bearing strata of Permo-Carboniferous system in Luxi and Jiyang area as an example. Acta Sedimentologica Sinica, 2005, 23(4): 639-645. DOI:10.3969/j.issn.1000-0550.2005.04.012 |
| [4] |
赵淑娥, 王华, 刘小龙, 等. 基于测井数据的高精度层序地层定量划分方法及其应用. 中南大学学报(自然科学版), 2013, 44(1): 233-240. ZHAO S E, WANG H, LIU X L, et al. A method for quantitative division of sequence stratigraphy with high-resolution using loggingdata and its application. Journal of Central South University(Science and Technology), 2013, 44(1): 233-240. |
| [5] |
张莹, 潘保芝, 黄布宙, 等. 测井资料小波变换在高分辨率层序地层划分中的应用. 物探化探计算技术, 2008, 30(1): 58-62. ZHANG Y, PAN B Z, HUANG B Z, et al. An application of wavelet transform to logging data for high resolution sequence stratigraphic division. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(1): 58-62. DOI:10.3969/j.issn.1001-1749.2008.01.013 |
| [6] |
任金峰, 廖远涛, 孙鸣, 等. 基于小波变换的高精度层序地层定量划分研究及应用. 地球物理学进展, 2013, 28(5): 2651-2658. REN J F, LIAO Y T, SUN M, et al. A method for quantitative division of sequence stratigraphy with high-resolution based on wavelet transform and its application. Progress in Geophysics, 2013, 28(5): 2651-2658. |
| [7] |
付文钊, 余继峰, 杨锋杰, 等. 小波变换与Hilbert-Huang变换应用于层序划分的比较. 煤炭学报, 2013, 38(增刊2): 434-441. FU W Z, YU J F, YANG F J, et al. Comparative study of the application of wavelet transform and Hilbert-Huang transform to the demarcation of sequences. Journal of China Coal Society, 2013, 38(Suppl 2): 434-441. |
| [8] |
徐敬领, 王贵文, 刘洛夫, 等. 基于经验模态分解法的层序地层划分及对比研究. 石油物探, 2010, 49(2): 182-186. XU J L, WANG G W, LIU L F, et al. Study on sequence stratigraphic division and correlation based on method of empirical mode decomposition. Geophysical Prospecting for Petroleum, 2010, 49(2): 182-186. DOI:10.3969/j.issn.1000-1441.2010.02.013 |
| [9] |
赵妮, 李瑞, 陈立军. 经验模态分解法在测井层序界面识别中的应用. 测井技术, 2014, 38(4): 474-479. ZHAO N, LI R, CHEN L J. Application of Empirical Mode Decomposition(EMD) to interface identification of logging sequence strata. Well Logging Technology, 2014, 38(4): 474-479. DOI:10.3969/j.issn.1004-1338.2014.04.019 |
| [10] |
文政, 朱筱敏, 金明玉, 等. 基于测井数据Hilbert-Huang变换的地层层序划分. 测井技术, 2007, 31(6): 533-536. WEN Z, ZHU X M, JIN M Y, et al. Demarcating stratigraphic sequence based on Hilbert-Huang transform of well-logging data. Well Logging Technology, 2007, 31(6): 533-536. DOI:10.3969/j.issn.1004-1338.2007.06.007 |
| [11] |
HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis. Proceedings of the Royal Society, 1998, 454: 903-995. DOI:10.1098/rspa.1998.0193 |
| [12] |
XUE Y J, CAO J X, DU H K, et al. Does mode mixing matter in EMD-based highlight volume methods for hydrocarbon detection? Experimental evidence. Journal of Applied Geophysics, 2016, 132: 193-210. DOI:10.1016/j.jappgeo.2016.07.017 |
| [13] |
贾瑞生, 赵同彬, 孙红梅, 等. 基于经验模态分解及独立成分分析的微震信号降噪方法. 地球物理学报, 2015, 58(3): 1013-1023. JIA R S, ZHAO T B, SUN H M, et al. Micro-seismic signal denoising method based on Empirical Mode Decomposition and independent component analysis. Chinese Journal of Geophysics, 2015, 58(3): 1013-1023. |
| [14] |
李彦军, 胡祥云, 何展翔. HHT变换在地球物理中的应用现状及前景. 工程地球物理学报, 2010, 7(5): 537-544. LI Y J, HU X Y, HE Z X. Application situation and prospects of Hilbert-Huang Transform in geophysics. Chinese Journal of Engineering Geophysics, 2010, 7(5): 537-544. |
| [15] |
WANG T, ZHANG M C, YU Q H, et al. Comparing the application of EMD and EEMD on time-frequency analysis of seimic signal. Journal of Applied Geophysics, 2012, 83(6): 29-34. |
| [16] |
时世晨, 单佩韦. 基于EEMD的信号处理方法分析和实现. 现代电子技术, 2011, 34(1): 88-90. SHI S C, SHAN P W. Signal processing method based on Ensemble Empirical Mode Decomposition. Modern Electronics Technique, 2011, 34(1): 88-90. DOI:10.3969/j.issn.1004-373X.2011.01.027 |
| [17] |
YEH J R, SHIEH J S, HUANGN E. Complementary Ensemble Empirical Mode Decomposition:a novel noise enhanced data analysis method. Advances in Adaptive Data Analysis, 2010, 2(2): 135-156. DOI:10.1142/S1793536910000422 |
| [18] |
GACI S. A new Ensemble Empirical Mode Decomposition (EEMD) denoising method for seismic signals. Energy Procedia, 2016, 97: 84-91. DOI:10.1016/j.egypro.2016.10.026 |
| [19] |
朱剑兵. 基于测井资料的高分辨率层序旋回划分方法探讨. 油气地球物理, 2011, 9(4): 6-11. ZHU J B. The discussion on the division methods of high resolution sequence cycle based on logging data. Petroleum Geophysics, 2011, 9(4): 6-11. |
| [20] |
刘腾, 王军, 张京思, 等. 地震Wheeler域变换结合时频分析技术用于渤海油田岩性油气藏描述. 岩性油气藏, 2018, 30(1): 124-132. LIU T, WANG J, ZHANG J S, et al. Application of Wheeler Transform combined with time-frequency analysis technology to lithologic reservoir characterization of Bohai Oilfield. Lithologic Reservoirs, 2018, 30(1): 124-132. |
| [21] |
李振春, 刁瑞, 韩文功, 等. 线性时频分析方法综述. 勘探地球物理进展, 2010, 33(4): 239-246. LI Z C, DIAO R, HAN W G, et al. Review on linear timefrequency analysis methods. Progress in Exploration Geophysics, 2010, 33(4): 239-246. |
| [22] |
吴淑玉, 刘俊. 基于时频分析的高分辨率层序地层. 海洋地质与第四纪地质, 2015, 35(4): 197-207. WU S Y, LIU J. High resolution sequence stratigraphic study basic on time-frequency analysis. Marine Geology & Quaternary Geology, 2015, 35(4): 197-207. |
| [23] |
邓继新, 王尚旭, 伍向阳. 渤海湾盆地东营凹陷砂岩储层地震特征及对岩石结构的指示. 石油与天然气地质, 2009, 30(3): 294-299. DENG J X, WANG S X, WU X Y. Seismic properties of reservoir sand stones and their implication to rock texture in the Dongying Sag, the Bohai Bay Basin. Oil & Gas Geology, 2009, 30(3): 294-299. DOI:10.3321/j.issn:0253-9985.2009.03.007 |
| [24] |
王伟庆, 刘宁, 田方. 东营凹陷牛庄地区沙三段层序地层分析. 地层学杂志, 2007, 31(增刊2): 567-572. WANG W Q, LIU N, TIAN F. Sequence stratigraphic analysis of the member 3 of Shahejie Formation in the Niuzhuang area of the Dongying Depression. Journal of Stratigraphy, 2007, 31(Suppl 2): 567-572. |
| [25] |
姜在兴, 杨伟利, 操应长. 东营凹陷沙河街组三段-二段下亚段沉积层序及成因. 石油与天然气地质, 2002, 23(2): 127-129. JIANG Z X, YANG W L, CAO Y C. Origin and sedimentary sequence of Es3-Es2 in Shahejie Formation of Dongying Depression. Oil & Gas Geology, 2002, 23(2): 127-129. DOI:10.3321/j.issn:0253-9985.2002.02.004 |
| [26] |
操应长, 姜在兴, 夏斌, 等. 陆相断陷湖盆T-R层序的特点及其控制因素——以东营凹陷古近系沙河街组三段层序地层为例. 地质科学, 2004, 39(1): 111-122. CAO Y C, JIANG Z X, XIA B, et al. Characters and controlling factors of T-R sequence in lacustrine deposits of rift basin:an example from the Dongying Depression, eastern China. Chinese Journal of Geology, 2004, 39(1): 111-122. DOI:10.3321/j.issn:0563-5020.2004.01.012 |
 2018, Vol. 30
2018, Vol. 30




