在地表复杂地区,近地表低降速层速度和厚度变化较大,建模时无法准确刻画近地表速度结构是长波长静校正产生的主要原因[1-6]。目前,静校正方法发展很快,折射静校正方法是建立在水平均匀层状介质的假设基础之上[7],复杂地表区近地表的情况又无法满足这个假设前提[8-9]。层析静校正技术由Amorim等[10]首次应用到野外静校正;Squires等[11]指出层析成像可解决由近地表速度变化引起的静态时移和构造成像;Rajasekaran等[12]给出了考虑反射数据和折射数据的约束层析静校正;Zhang等[13]给出了非线性折射层析静校正方法;李录明等[14]实现了初至波表层模型的层析反演,可以适应速度横向变化问题,反演的近地表模型精度较高。层析静校正是目前有效的静校正方法且应用广泛,但是该方法根据扰动理论反演得到的是一个等效模型,受初始速度模型的影响较大,因此,应采用先验信息约束层析反演近地表建模[15]。初始速度模型建立时,微测井资料在点上能准确反映低速层信息,受探测深度限制,刻画降速层速度的能力较低,而小折射资料对降速层速度有很好地反映,但小折射刻画高速层顶界面形态受小折射排列长度的限制,特别是当高速层顶界面起伏较大和高速层速度横向变化较大时,高速层顶界面的形态刻画不准确,而无法彻底解决长波长静校正问题。
为此,采用分层约束建模方法建立近地表速度结构,首先利用微测井建立低速层速度模型v0,然后再用小折射、VSP建立降速层速度模型v1,作为全局寻优非线性层析反演的初始模型,进行分层约束层析反演近地表建模,建立高精度的近地表速度结构[16],并通过VSP测井及实钻井深度约束确定高速层顶面的形态[17],两者结合以期更好地解决复杂地表区长波长静校正问题。
1 分层约束近地表速度结构建模策略微测井能比较直观地描述井下到地面的波场传播,可直接获得精确的低速层厚度和速度变化信息。微测井通常作为先验地表信息来约束反演低速层速度,但由于受复杂近地表条件等因素的限制,微测井点横向分辨率较低且分布不均匀,再加上微测井观测深度有限,很难直接约束反演到近地表降速层速度结构的变化。因此,采用分层约束层析反演近地表建模策略,来逐步建立高精度的近地表速度结构。
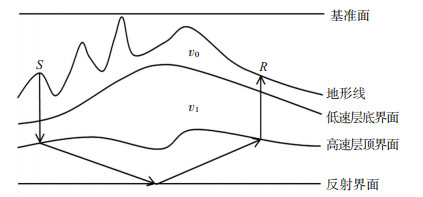
近地表速度结构分为上、下2个相邻区域:上部为地表风化低速层v0,由速度很低的疏松地层组成;下部为地层较为致密的降速层v1,且逐步向高速层过渡,基准面校正示意图如图 1所示。在低速层建模中,微测井资料具有准确的低速层速度信息,根据研究区地质资料特征,通过人机交互解释微测井资料并建立合理的近地表低速层v0速度模型,获得尽量优化并接近野外实际情况的模型。对于复杂地表速度结构,仅用微测井建立低速层速度信息来约束反演近地表速度结构还远远不够。小折射可以快速测定低降速层厚度,追踪高速层的埋深,但当折射层太薄或速度差太小时,小折射也很难测定低降速带速度结构;另外,用小折射来刻画高速层顶界面还受到小折射排列长度的限制。因此,用小折射建立降速层v1的速度,具体实现时充分利用大炮初至信息和VSP来解决排列长度受限的问题。在建立的低速层v0基础上,分层建立降速层v1速度结构模型,克服只用小折射资料建立v1速度信息的不足,提高了v1的精度。利用地质统计技术对高速层的顶界面及在反演基础上借助VSP测井数据进行优化,估算出最有可能的高速层顶界面空间形态,进而刻画高速层顶界面形态。
|
下载eps/tif图 图 1 基准面校正示意图 S.炮点;R.接收点 Fig. 1 Schematic diagram of datum correction |
基于低速层v0、降速层v1速度结构所建立的近地表速度结构更加符合实际地质情况,作为层析反演近地表建模的初始模型,避免了简单常速模型造成的多解性,提高了层析反演的稳定性。在层析反演中,M条射线和N个未知数建立的层析方程组可表示为
| $ \mathit{\boldsymbol{A}}\;\Delta \;\mathit{\boldsymbol{S}} = \Delta \mathit{\boldsymbol{T}} $ | (1) |
式中:A,Δ S和Δ T分别为Jacob矩阵、慢度修正量和旅行时残差,可表示为
| $ \mathit{\boldsymbol{A = }}\left[ {\begin{array}{*{20}{c}} {\frac{{\partial {t_1}}}{{\partial {s_1}}}}&{\frac{{\partial {t_1}}}{{\partial {s_2}}}}& \cdots &{\frac{{\partial {t_1}}}{{\partial {s_N}}}}\\ {\frac{{\partial {t_2}}}{{\partial {s_1}}}}&{\frac{{\partial {t_2}}}{{\partial {s_2}}}}&{}&{\frac{{\partial {t_2}}}{{\partial {s_N}}}}\\ \vdots&\vdots &{}& \vdots \\ {\frac{{\partial {t_M}}}{{\partial {s_1}}}}&{\frac{{\partial {t_M}}}{{\partial {s_2}}}}& \cdots &{\frac{{\partial {t_M}}}{{\partial {s_N}}}} \end{array}} \right], \Delta \mathit{\boldsymbol{S = }}\left[ {\begin{array}{*{20}{c}} {\Delta {s_1}}\\ {\Delta {s_2}}\\ \vdots \\ {\Delta {s_N}} \end{array}} \right], \Delta \mathit{\boldsymbol{T}}\left[ {\begin{array}{*{20}{c}} {\Delta {t_1}}\\ {\Delta {t_2}}\\ \vdots \\ {\Delta {t_N}} \end{array}} \right] $ | (2) |
L个约束条件建立的约束方程组可表示为
| $ \mathit{\boldsymbol{C}}\;\Delta \;\mathit{\boldsymbol{S}} = \mathit{\boldsymbol{F}} $ | (3) |
其中:
| $ \mathit{\boldsymbol{C = }}\left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}& \cdots &{{c_{1N}}}\\ {{c_{21}}}&{{c_{22}}}&{}&{{c_{2N}}}\\ \vdots&\vdots &{}& \vdots \\ {{c_{L1}}}&{{c_{L2}}}&{}&{{c_{LN}}} \end{array}} \right], \Delta \mathit{\boldsymbol{S = }}\left[ {\begin{array}{*{20}{c}} {\Delta {s_1}}\\ {\Delta {s_2}}\\ \vdots \\ {\Delta {s_N}} \end{array}} \right], \mathit{\boldsymbol{F = }}\left[ {\begin{array}{*{20}{c}} {{f_1}}\\ {{f_2}}\\ \vdots \\ {{f_L}} \end{array}} \right] $ | (4) |
在初至波层析中,假如
| $ {c_{ij}} = \left\{ {\begin{array}{*{20}{c}} 1&{i = j}\\ 0&{i \ne j} \end{array}} \right., {f_i} = \widetilde {{s_i}} - {s_i} $ | (5) |
式中:si为第i个单元上一次迭代层析反演速度(慢度)值。
进行速度层析时,利用式(2)对式(1)进行约束,则正则化反演目标函数为
| $ e = {e_1} + \lambda {e_2} \to \min $ | (6) |
式中:e为总目标函数;e1 = (A ΔS - ΔT) T(A ΔS - Δ T)为观测数据目标函数;e2 = (C Δ S - F)T(C Δ S - F)为先验约束条件的目标函数;λ为正则化因子(或权重因子)。
当总目标函数e最小时,计算出的ΔS就是最优解。从总目标函数中可看出,正则化因子λ= 0,相当于没有约束,λ越大,相当于约束方程在总目标函数中所占权重越大,约束越强。λ的不同取值对反演结果具有重要影响,而且在反演中,存在一个最佳折衷正则化因子,使得反演结果最佳。在外部输入经验值的常规做法是,须要选取不同的λ值进行多次实验才能够取得较为满意的结果。
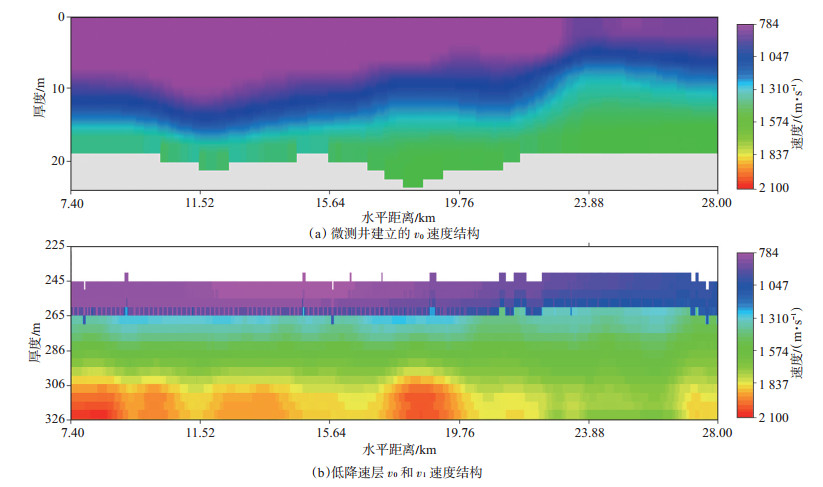
图 2为用上述方法建立的近地表速度结构。其中,图 2(a)为用微测井资料建立的低速层v0速度;图 2(b)为在v0速度结构基础上,用小折射、大炮初至结合VSP建立的低降速层速度结构,可以用该低降速层速度结构作为初始速度对层析反演进行约束。
|
下载eps/tif图 图 2 微测井、小折射建立的近地表速度结构 Fig. 2 Construction of near-surface velocity structure with micro-logging and short-refraction |
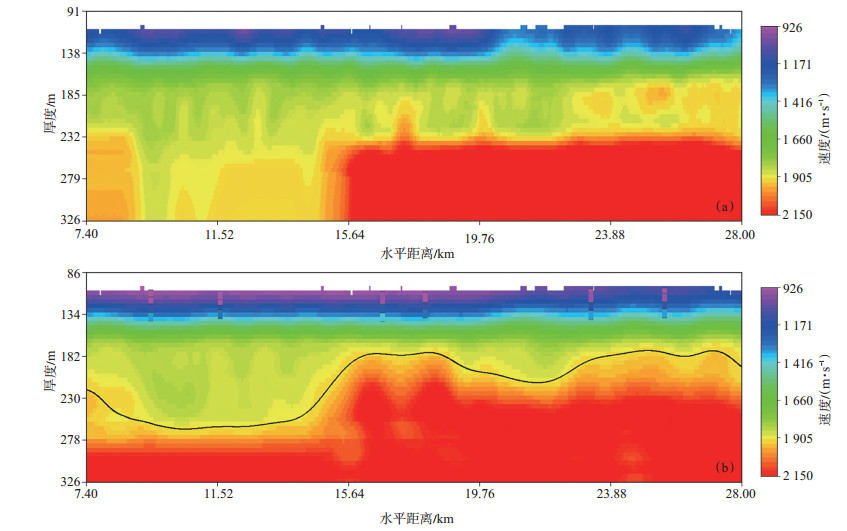
用已建立的低降速层速度进行分层约束层析反演,与图 3(a)无约束层析反演建立近地表速度结构相比,图 3(b)分层约束层析反演建立的近地表速度结构反映的浅层低速速度信息更为丰富,低速层底界面的空间分布更符合实际地表情况,与已有微测井标定的吻合度明显提高。
|
下载eps/tif图 图 3 无约束(a)和分层约束(b)层析反演建立的近地表速度结构 Fig. 3 Near-surface velocity structure inversed without (a) and with (b) stratified velocity constraint |
通常情况下,从地表到高速层顶(v1底)界面,用近地表速度进行逐层剥离来计算炮点S的静校正量,再用充填速度回填到固定基准面来计算检波点R的静校正量。对于在炮点S激发、检波点R接收的地震记录来讲,总静校正量为检波点静校正量与炮点静校正量之和。因此,无论是炮点还是检波点静校正的求取,都与高速层顶界面息息相关。也就是说,高速层顶界面形态刻画的准确与否,直接影响到静校正的应用效果。传统方法是通过常速度追踪确定一个降速层底界面,其精度依赖于层析反演的降速层底界面速度结构,然而层析反演很难精确反演到降速层底界面的空间形态。
为了精确刻画低降速层速度空间结构,在分层约束层析反演近地表建模基础上,再采用VSP测井及实钻井速度深度信息,通过协克里金方法优化得到高精度的速度结构模型及降速层底界面的空间形态。
| $ Z_0^* = \sum\limits_{i = 1}^n {{\alpha _i}{x_i} + \sum\limits_{j = 1}^m {{\beta _j}{y_j}} } $ | (7) |
式中:Z0*为最终速度结构模型;x1,x2,…,xn为分层约束层析反演得到的近地表速度结构模型的n个样本数据;y1,y2,…,ym为为用VSP测井及实钻井得到速度的m个样本数据;a1,a2,…,an和β1,β2,…,βm为需要确定的协克里金加权系数。
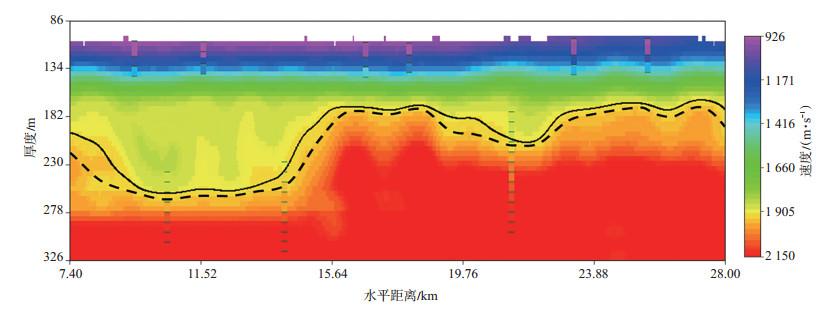
图 4是基于VSP及实测井深约束,采用协克里金方法优化得到的高精度速度模型及高速层顶界面的空间形态,其中实线为协克里金方法优化得到高速层顶界面形态,虚线为用分层约束层析反演得到的高速层顶界面形态,优化后与VSP测井及实钻井更吻合,很好地解决了实际资料的长波长静校正问题。
|
下载eps/tif图 图 4 速度模型结构及高速层顶界面形态 Fig. 4 Near-surface velocity model and the top interface morphology of high velocity layer |
准噶尔盆地玛湖凹陷X地区是典型的地层-岩性圈闭及断层-地层岩性复合型圈闭,地表覆盖有盐湖、盐碱地、沼泽地和公益林等,局部地方高程变化剧烈,近地表速度结构变化较大,静校正问题严重,直接影响了成像质量和地层形态,为查清三叠系百口泉组与二叠系不整合面的精细特征,准确落实三叠系、二叠系的低幅度构造,重新采集了三维地震资料,但受地表条件限制,三维资料炮点分布不规则,造成覆盖次数不均匀和部分局域缺少近偏移距资料,给近地表建模带来了很大困难。因此,为了建立准确的近地表速度结构模型,采用了分层约束建模思路,首先用微测井建立低速层速度结构,然后用小折射、VSP联合建立降速层速度模型,作为全局寻优非线性层析反演的初始模型,进行分层约束层析反演近地表建模,从而建立了高精度近地表速度结构。同时,对于降速层底界面的确定,传统方法是通过常速追踪一个速度界面,其精度依赖于层析反演的近地表速度结构,X地区对于降速层底界面形态的刻画受实际资料射线密度的影响较大,为了精确刻画降速层底界面空间形态,基于VSP及实测井深约束,采用了协克里金方法对降速层底界面的空间形态进行优化。通过以上2种策略,很好地解决了X地区的长波长静校正问题,在岩性油气藏勘探中得到了很好的应用。图 5为约束层析反演前、后近地表速度结构对应静校正的叠加剖面。其中:图 5(a)为无约束层析反演、常规高速层顶界静校正叠加剖面;图 5(b)为用本次研究方法求得的静校正量叠加剖面,对比可看出采用本次研究方法计算的静校正量能很好地解决本地区的长波长静校正问题。
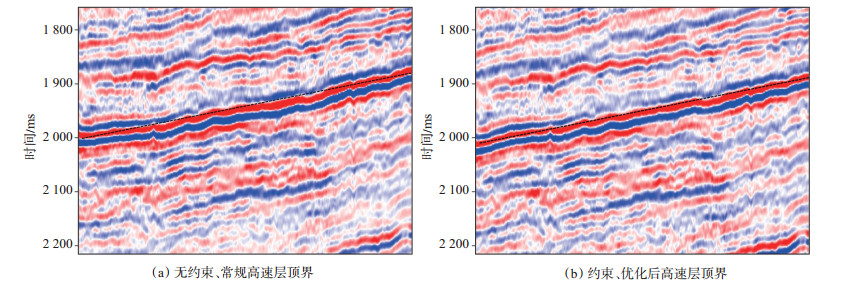
|
下载eps/tif图 图 5 约束层析反演前、后近地表速度结构对应静校正叠加剖面 Fig. 5 Static-corrected stack sections using conventional method and stratified constrained near-surface velocity modeling method |
(1)采用分层建模思路建立初始模型,通过分层约束全局寻优非线性层析反演方法,可提高近地表速度结构的精度。
(2)基于VSP及实测井深约束,采用协克里金方法优化降速层底界面的空间形态。
(3)通过以上2种策略,能够很好地解决复杂地表区长波长静校正问题,在准噶尔盆地玛湖凹陷X地区岩性油气藏勘探中得到了很好的应用,较好地解决了该地区的长波长静校正问题。
| [1] |
王西文, 雍学善, 王宇超, 等. 面对重点勘探领域的地震技术研究和应用实效. 岩性油气藏, 2010, 22(3): 83-90. WANG X W, YONG X S, WANG Y C, et al. Study and application of seismic technologies for key exploration field. Lithologic Reservoirs, 2010, 22(3): 83-90. DOI:10.3969/j.issn.1673-8926.2010.03.016 |
| [2] |
祖云飞, 冯泽元, 李振华. 长波长静校正问题的探讨和实例分析. 天然气工业, 2007, 27(增刊1): 195-198. ZU Y F, FENG Z Y, LI Z H. A long wave-length static correction study and example analysis. Natural Gas Industry, 2007, 27(Suppl 1): 195-198. |
| [3] |
钟德盈. 近地表模型静校正. 石油地球物理勘探, 1992, 27(4): 454-463. ZHONG D Y. Static correction using near surface model. Oil Geophysical Prospecting, 1992, 27(4): 454-463. |
| [4] |
林依华, 张中杰, 尹成, 等. 复杂地形条件下静校正的综合寻优. 地球物理学报, 2003, 46(1): 101-106. LIN Y H, ZHANG Z J, YIN C, et al. Hybrid optimization of static estimation in complex topography. Chinese Journal of Geophysics, 2003, 46(1): 101-106. DOI:10.3321/j.issn:0001-5733.2003.01.016 |
| [5] |
王志刚, 刘志伟, 王彦春, 等. 复杂近地表区综合长波长静校正方法. 石油地球物理勘探, 2014, 49(3): 480-485. WANG Z G, LIU Z W, WANG Y C, et al. An integrated longwavelength static correction method for complex near-surface area. Oil Geophysical Prospecting, 2014, 49(3): 480-485. |
| [6] |
吴杰, 苏勤, 王建华. 层析静校正技术在柴北缘地区的应用. 岩性油气藏, 2008, 20(3): 79-82. WU J, SU Q, WANG J H. Application of tomographic static correction in northern margin of Qaidam Basin. Lithologic Reservoirs, 2008, 20(3): 79-82. DOI:10.3969/j.issn.1673-8926.2008.03.016 |
| [7] |
戴云, 张建中. 长波长静校正问题的一种解决方法. 石油地球物理勘探, 2000, 35(3): 315-325. DAI Y, ZHANG J Z. A method for long-wavelength static correction. Oil Geophysical Prospecting, 2000, 35(3): 315-325. DOI:10.3321/j.issn:1000-7210.2000.03.006 |
| [8] |
张永峰, 王鹏, 张亚兵, 等. 基于变差函数的高精度静校正融合技术及其应用. 岩性油气藏, 2015, 27(3): 108-114. ZHANG Y F, WANG P, ZHANG Y B, et al. Research and application of high-precision merged static correction technology based on variogram. Lithologic Reservoirs, 2015, 27(3): 108-114. DOI:10.3969/j.issn.1673-8926.2015.03.017 |
| [9] |
商昌亮, 付守献. 黄土塬山地三维地震勘探应用实例. 岩性油气藏, 2007, 19(3): 106-110. SHANG C L, FU S X. Application of 3D seismic survey in loess tableland. Lithologic Reservoirs, 2007, 19(3): 106-110. DOI:10.3969/j.issn.1673-8926.2007.03.019 |
| [10] |
AMORIM W N, HUBRAL P, TYGEL M. Computing field statics with the help of seismic tomography. Geophysical Prospecting, 1987, 35: 907-919. DOI:10.1111/gpr.1987.35.issue-8 |
| [11] |
SQUIRES L J, BLAKESLEE S N, STOFFA P L. Effects of static on tomographic velocity reconstructions. Geophysics, 1992, 57: 353-362. DOI:10.1190/1.1443249 |
| [12] |
RAJASEKARAN S, MCMECHAN G A. Tomographic imaging of the spatial distribution of statics. SEG Technical Program Expanded Abstracts, 1995, 61(4): 700-703. |
| [13] |
ZHANG J, TOKSOZ M N. Nonlinear refraction traveltime tomography. Geophysics, 1998, 63: 1726-1737. DOI:10.1190/1.1444468 |
| [14] |
李录明, 罗省贤. 复杂三维表层模型层析反演与静校正. 石油地球物理勘探, 2003, 38(6): 636-641. LI L M, LUO S X. Tomographic inversion for 3-D complex near-surface model and static correction. Oil Geophysical Prospecting, 2003, 38(6): 636-641. DOI:10.3321/j.issn:1000-7210.2003.06.010 |
| [15] |
王孝, 贺振华, 王述江, 等. 多信息约束层析反演静校正技术及其应用. 天然气地球科学, 2010, 21(2): 316-320. WANG X, HE Z H, WANG S J, et al. Technology of static correction for multi information constrained tomographic inversion and its application. Natural Gas Geoscience, 2010, 21(2): 316-320. |
| [16] |
刘振峰. 油气地震地质模型述评. 岩性油气藏, 2018, 30(1): 19-29. LIU Z F. Review on oil and gas seismogeology models. Lithologic Reservoirs, 2018, 30(1): 19-29. DOI:10.3969/j.issn.1673-8926.2018.01.002 |
| [17] |
周志军, 薛江龙, 赵立斌. 数值模拟拟合精度方法研究. 岩性油气藏, 2016, 28(1): 101-105. ZHOU Z J, XUE J L, ZHAO L B. Numerical simulation fitting technology:a case study from Longhupao Oilfield. Lithologic Reservoirs, 2016, 28(1): 101-105. DOI:10.3969/j.issn.1673-8926.2016.01.013 |
 2018, Vol. 30
2018, Vol. 30



