2. 中国科学院 力学研究所, 北京 100190;
3. 中国科学院大学, 北京 100049
2. Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着水平井技术和多级压裂技术的不断提高,页岩气的开发主要依赖于压裂段之间相互沟通的裂缝网络,从而与更大面积的储层相互接触[1-3]。中国及北美的页岩气水平井间距一般为200~300 m,加密井井距越来越近,亟须深入认识井间干扰特征,探究合理井距。Ajani等[4]利用Arkoma盆地179口井的压裂和生产数据,分析了井间干扰对产能的影响,计算了邻井开发对本井气产量的损失,确定了最强的干扰方向;Kim等[5]基于Eagle Ford页岩气田的地球物理、完井和开发资料,提出了一种关于页岩气藏的数值模拟方法,研究了压裂缝繁殖及其与天然裂缝网络的相互作用,评价了原地应力的大小和方位。
针对页岩气多段压裂水平井渗流特征问题,国内外许多学者建立了多重线性流区域耦合的宏观渗流模型。Bello等[6]采用层状双重孔隙模型和Warren-Root双重孔隙模型分析了页岩储层内多段压裂水平井的压力响应和生产动态;Ozkan等[7]和Al-Rbeawi等[8]将改造后的页岩储层划分为压裂裂缝区、压裂缝之间的SRV(改造体积)区和未改造基质区,这3个区域中的流动均简化为一维线性流动,然后建立了三线性流模型;Stalgorova等[9]和Zhang等[10]在此基础上补充考虑了压裂缝之间未被诱导裂缝改造的区域,提出了耦合5个区域的页岩气流动模型;Zeng等[11]在5个区域复合线性流模型的基础上又进行了细分,提出了耦合7个区域的渗流模型;Wang等[12]在这些耦合模型的基础上又考虑到了耦合区受应力敏感的影响。各区域模型中可采用等效渗透率来简化表征SRV区域内的解吸附、扩散等现象对渗流的影响,在此基础上进一步细分得到5个区域或7个区域模型,但增加的区域中物性参数很难获得,并且与相邻区域差别较小[13-16]。因此,建立压裂裂缝区域、SRV区域和未改造基质区域的三重区域模型,并基于PEBI网格和有限体积法进行数值求解,模拟分析连通渗透率和激动量等因素对干扰试井测试结果及压力场分布特征的影响,以期对焦页7井组的干扰试井测试数据进行实例应用。
1 页岩气多段压裂水平井渗流模型 1.1 物理模型由于储层内压裂改造区域与未改造区域的孔渗差异较大,压裂后的页岩储层采取分区域表征的方法,主要包括压裂裂缝区域、诱导微裂缝发育的SRV区域,以及未压裂改造的基质区域(图 1)。假设条件:①页岩储层内仅存在等温状态下单相气体流动;②压裂裂缝内仅存在黏性流,且服从达西渗流规律[17],忽略裂缝内纵向上的流动;③ SRV区域等效为双重介质,单井各段SRV区域之间相互重叠;④未改造的基质区域视为均质超低渗介质。
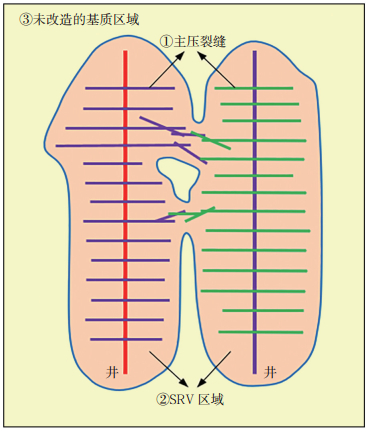
|
下载eps/tif图 图 1 多重区域耦合的页岩储层物理模型 Fig. 1 Physical model of multi-region coupled shale reservoir |
假设压裂主裂缝与SRV区域和井筒之间均存在流体交换,定义生产井与压裂缝之间的边界为Γ1,SRV区域与压裂裂缝交界处的边界为Γ2,据此建立了有限导流压裂裂缝内的流动方程
| $ {\nabla ^2}{m_{\rm{F}}} = - \frac{{{\varphi _{\rm{F}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{\rm{F}}}}}\frac{{\partial {m_{\rm{F}}}}}{{\partial t}} $ | (1) |
式中:mF为气体拟压力(下标F为压裂缝标记),MPa2/mPa·s;$φ$为孔隙度;kF为有限导流压裂裂缝的渗透率,mD;μg为气体黏度,mPa·s;cg为气体压缩系数,MPa-1;t为时间,d。
初始条件:
| $ {\left. {{m_{\rm{F}}}} \right|_{t = 0}} = {m_{\rm{i}}} $ | (2) |
式中:mi为初始气体拟压力,MPa2/mPa·s。
内边界条件包括
(1) 定压力边界条件:
| $ {\left. {{m_{\rm{F}}}} \right|_{{\mathit{\Gamma }_1}}} = {m_{\rm{w}}} $ | (3) |
式中:mw为井筒气体拟压力,MPa2/mPa·s。
(2) 定产量边界条件:
| $ {\left. {\frac{{\partial m}}{{\partial n}}} \right|_{{\mathit{\Gamma }_1}}} = {q_{{\rm{iw,F}}}} $ | (4) |
式中:n为边界法向量;qiw, F为本井压裂缝与本井井筒之间的流体交换量,m3/d。对于未与井筒直接连接的压裂缝,qiw, F为0 m3/d,本井压裂缝与邻井压裂缝没有连通时,qiw, F为0 m3/d。
外边界条件为
| $ {\left. {{m_{{\rm{S,f}}}}} \right|_{{\mathit{\Gamma }_2}}} = {\left. {{m_{\rm{F}}}} \right|_{{\mathit{\Gamma }_2}}} $ | (5) |
(1) 基质系统流动方程
由于SRV区域内压裂改造后的诱导微裂缝发育,因此,将SRV区域视为包含基质系统和裂缝系统的双重介质,那么基质内的流动方程为
| $ {\nabla ^2}{m_{{\rm{S,m}}}} - \alpha \left( {{m_{{\rm{S,m}}}} - {m_{{\rm{S,f}}}}} \right) = \frac{{{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{{\rm{S,m}}}}}}\frac{\partial }{{\partial t}}\left[ {{\varphi _{{\rm{S,m}}}} + \left( {1 - {\varphi _{{\rm{S,m}}}}} \right)\frac{{{M_{{\rm{S,g}}}}{V_{{\rm{S,L}}}}{m_{{\rm{S,L}}}}}}{{{V_{{\rm{std}}}}{{\left( {{m_{{\rm{S,L}}}} + {m_{{\rm{S,m}}}}} \right)}^2}}}} \right] $ | (6) |
式中:mS, m和mS, f分别为SRV基质系统和裂缝系统的气体拟压力,MPa2/mPa·s;α为窜流系数,(m3· mPa·s)/MPa2;VS, L为朗格缪尔气体体积,m3/kg;Vstd为标准温度和压力条件下的气体摩尔体积,m3/kmol;mS, L为朗格缪尔气体拟压力,MPa2/mPa·s;MS, g为气体的摩尔重量,kg/kmol;$φ$S, m为SRV区域基质内的孔隙度。
(2) 裂缝系统流动方程
由于SRV区域内微裂缝非常发育,如何在渗流模型中等效表征裂缝网络一直是难以解决的问题。为此,众多学者假设裂缝网络的发育和展布满足分形特征,提出了表征天然裂缝网络的分形扩散模型[18]。SRV区域裂缝介质内气体主要以游离气形式存在,所以裂缝介质中仅考虑气体黏性流和努森扩散,并采用视渗透率等效表征裂缝介质的渗透性[19]。
| $ {k_{{\rm{S,f}}}} = \frac{{{b^3}}}{{12c}}\left( {1 + \beta {K_{\rm{n}}}} \right)\left( {1 + \frac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}} \right) $ | (7) |
式中:kS, f为视渗透率,mD;β为稀薄系数;b为平均裂缝开度,m;c为平均裂缝间距,m;Kn为努森数。
假设井筒仅与压裂缝存在流体交换,忽略SRV区域裂缝系统与井筒之间的直接流体交换,定义SRV区域裂缝系统与未改造基质区域界面为Γ3,那么SRV区域裂缝系统内的流动方程为
| $ {\nabla ^2}{m_{{\rm{S,f}}}} + \alpha \left( {{m_{{\rm{S,m}}}} - {m_{{\rm{S,f}}}}} \right) = \frac{{{\varphi _{{\rm{S,f}}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{{\rm{S,f}}}}}}\frac{{\partial {m_{{\rm{S,f}}}}}}{{\partial t}} $ | (8) |
初始条件:
| $ {\left. {{m_{{\rm{S,m}}}}} \right|_{t = 0}} = {\left. {{m_{{\rm{S,f}}}}} \right|_{t = 0}} = {m_{\rm{i}}} $ | (9) |
内边界条件:
| $ {\left. {{m_{{\rm{S,}}f}}} \right|_{{\mathit{\Gamma }_2}}} = {\left. {{m_{\rm{F}}}} \right|_{{\mathit{\Gamma }_2}}} $ | (10) |
外边界条件:
| $ {\left. {{m_{{\rm{S,}}f}}} \right|_{{\mathit{\Gamma }_3}}} = {\left. {{m_{\rm{M}}}} \right|_{{\mathit{\Gamma }_3}}} $ | (11) |
页岩气藏储层富含大量的干酪根有机质,干酪根中生成的烃类气体满足自身饱和吸附后,由干酪根微孔扩散到烃浓度相对较低的无机基质孔隙空间中。
| $ {k_{{\rm{M,a}}}} = {k_0}\left[ {1 + \frac{{128{K_{\rm{n}}}}}{{15{\pi ^2}}}{{\tan }^{ - 1}}\left( {4K_{\rm{n}}^{0.4}} \right)} \right]\left[ {1 + \frac{{4{K_{\rm{n}}}}}{{1 + {K_{\rm{n}}}}}} \right] $ | (12) |
由此可得努森扩散、吸附解吸和表面扩散等运移方式的干酪根介质连续性方程
| $ {\nabla ^2}{m_{\rm{M}}} = \frac{{{\varphi _{\rm{M}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{{\rm{M,a}}}}}}\frac{{\partial {m_{\rm{M}}}}}{{\partial t}} $ | (13) |
式中:mM为基质的气体拟压力,MPa2(/ mPa·s)。
初始条件:
| $ {\left. {{m_{\rm{M}}}} \right|_{t = 0}} = {m_{\rm{i}}} $ | (14) |
内边界条件:
| $ {\left. {{m_{S,f}}} \right|_{{\mathit{\Gamma }_3}}} = {\left. {{m_M}} \right|_{{\mathit{\Gamma }_3}}} $ | (15) |
外边界条件:
| $ {\left. {\frac{{\partial {m_{\rm{M}}}}}{{\partial n}}} \right|_{{\mathit{\Gamma }_3}}} = 0 $ | (16) |
采用非结构化PEBI网格对求解区域进行网格划分,各网格中心节点与相邻网格中心节点的连线与交界面垂直,并在井和裂缝周围进行网格加密处理(图 2)。
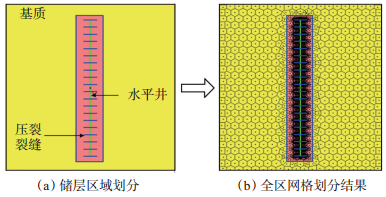
|
下载eps/tif图 图 2 页岩储层多重区域网格划分 Fig. 2 Multi-zone meshing of shale reservoirs |
采用有限体积法将储层区域离散成不重叠的控制容积,并使每个中心结点周围具有一定的控制容积。根据多重复合流动模型的渗流方程和边界条件,将待求解的偏微分方程对每一个控制容积积分,从而得出一组离散方程。
(1) 压裂裂缝离散流动方程
| $ \sum\limits_i^N {{{\left( {A\frac{{m_{\rm{F}}^a - m_{\rm{F}}^i}}{{{L_{{\rm{a}},i}}}}} \right)}_i}} = - {\left( {\frac{{{\varphi _{\rm{F}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{\rm{F}}}}}} \right)^{n + 1}}\frac{{m_{\rm{F}}^{n + 1} - m_{\rm{F}}^n}}{{\Delta t}}\Delta V $ | (17) |
式中:A为控制体面积,m2;L为2个控制体之间中心点的距离,m;ΔV为控制体的体积,m3;N为周围有限体积单元总数;n为时间步长;i为周围有限体积单元编号。
(2) SRV区域的离散流动方程
SRV区域基质系统的离散流动方程为
| $ \begin{array}{l} \sum\limits_i^n {{{\left( {A\frac{{m_{{\rm{S,m}}}^a - m_{{\rm{S,m}}}^i}}{{{L_{{\rm{a}},i}}}}} \right)}_i}} - \alpha \left( {{m_{{\rm{S,m}}}} - {m_{{\rm{S,f}}}}} \right)\Delta V = - {\left( {\frac{{{\varphi _{\rm{F}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{\rm{F}}}}}} \right)^{n + 1}}\frac{{{{\left[ {{\varphi _{{\rm{S,m}}}} + \left( {1 - {\varphi _{{\rm{S,m}}}}} \right)\frac{{{M_{{\rm{S,g}}}}{m_{{\rm{S,L}}}}{V_{{\rm{S,L}}}}}}{{{V_{{\rm{std}}}}{{\left( {{m_{{\rm{S,L}}}} + {m_{{\rm{S,m}}}}} \right)}^2}}}} \right]}^{n + 1}}}}{{\Delta t}}\Delta V - \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\frac{{{{\left[ {{\varphi _{{\rm{S,m}}}} + \left( {1 - {\varphi _{{\rm{S,m}}}}} \right)\frac{{{M_{{\rm{S,g}}}}{m_{{\rm{S,L}}}}{V_{{\rm{S,L}}}}}}{{{V_{{\rm{std}}}}{{\left( {{m_{{\rm{S,L}}}} + {m_{{\rm{S,m}}}}} \right)}^2}}}} \right]}^n}}}{{\Delta t}}\Delta V \end{array} $ | (18) |
| $ \sum\limits_i^n {{{\left( {A\frac{{m_{{\rm{S,f}}}^a - m_{{\rm{S,f}}}^i}}{{{L_{{\rm{a}},i}}}}} \right)}_i}} - \alpha \left( {{m_{{\rm{S,m}}}} - {m_{{\rm{S,f}}}}} \right)\Delta V = - {\left( {\frac{{{\varphi _{\rm{F}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{\rm{F}}}}}} \right)^{n + 1}}\frac{{\left( {m_{{\rm{S,f}}}^{n + 1} - m_{{\rm{S,f}}}^n} \right)}}{{\Delta t}}\Delta V $ | (19) |
(3) 未改造基质区域的离散流动方程
| $ \sum\limits_i^n {{{\left( {A\frac{{m_{\rm{M}}^a - m_{\rm{M}}^i}}{{{L_{{\rm{a}},i}}}}} \right)}_i}} = - {\left( {\frac{{{\varphi _{\rm{F}}}{\mu _{\rm{g}}}{c_{\rm{g}}}}}{{{k_{\rm{F}}}}}} \right)^{n + 1}}\frac{{\left( {m_{\rm{M}}^{n + 1} - m_{\rm{M}}^n} \right)}}{{\Delta t}}\Delta V $ | (20) |
连通渗透率是指所有连通的压裂段之间储层的平均渗透率,可根据连通层段内压力传播的速度和幅度计算而得。为了对比不同连通渗透率下干扰试井的测试结果,分别假设连通渗透率为20 mD,5 mD和1 mD,并模拟不同条件下的干扰测试结果,以及不同连通渗透率情况下的模拟压力(图 3)。连通渗透率越高,连通层段内压降越小,压力扰动传播的速度越快,压降的幅度就越小。因为在地层物性较好的情况下,采出相同的气量,其储层压力下降的速度越慢。
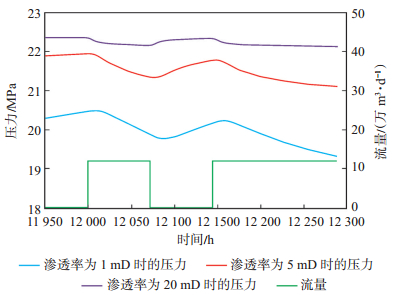
|
下载eps/tif图 图 3 不同连通渗透率情况下的模拟压力 Fig. 3 Simulated pressure under different connected permeability |
在未知合理激动量的条件下,对干扰试井的测试方案进行对比分析,将有利于优化试井方案。现选取激动量为6万m3/d,12万m3/d和24万m3/d进行方案对比,不同激动量情况下的模拟压力如图 4所示。激动量越大,连通层段内压降越明显,压降幅度就越大。因为相同地层物性条件下,采出越多的气量,储层压力下降的速度越快。
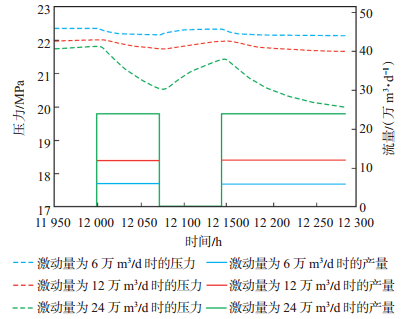
|
下载eps/tif图 图 4 不同激动量情况下的模拟压力 Fig. 4 Simulated pressure at different levels of production |
焦页7井组位于重庆市涪陵区焦石镇,是针对上奥陶统五峰组—下志留统龙马溪组下部页岩气层部署的开发水平井组,现有JY7-1 HF,JY7-2 HF和JY7-3 HF共3口井。JY7-1 HF井距JY7-2 HF井300 m,JY7-3 HF井距JY2 HF井740 m。为了充分认识JY7井组中井间干扰,针对焦页7井组开展干扰试井分析,每一口井上均安装高精度的井下压力计,然后3口井同时关井并恢复压力,之后JY7-2 HF井2次开井,1次关井,形成干扰脉冲,记录JY7-1 HF井的压力变化。
3.1 焦页7井组测试曲线特征干扰测试期间JY7-2 HF井的产量变化,以及JY7-1 H井的压力变化如图 5所示。从图中可以看出:激动井JY7-2 HF井开井生产时,JY7-1 HF井压力逐渐下降,当JY7-2 HF井关井后,JY7-1 HF井压力上升;当JY7-2 HF井再次开井生产时,JY7-1 HF井压力又下降,说明JY7-1 HF井和JY7-2 HF井是连通的。从2个拐点处可看到:当JY7-2 HF井关井后,JY7-1 HF井压力没有立即上升,而是继续下降了一段时间后再开始上升;当JY7-2 HF井开井后,JY7-1 HF井压力也持续上升了一段时间后才开始下降,说明压力干扰脉冲的传播需要一定的时间,这个时间的长短与连通段的导压系数及渗透率有关。
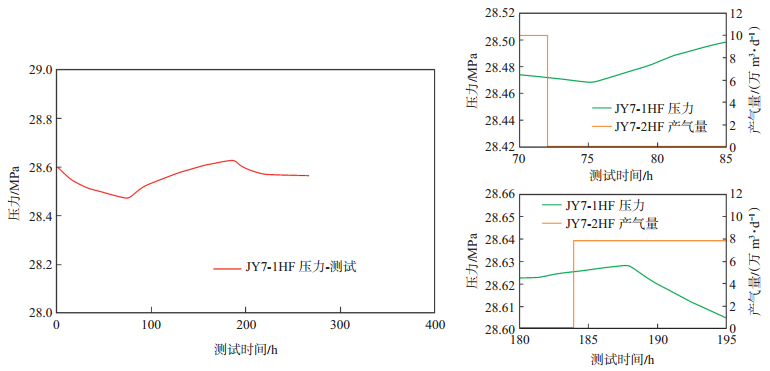
|
下载eps/tif图 图 5 干扰测试时响应井压力及激动井产量变化 Fig. 5 Pressure and production variation during interference test |
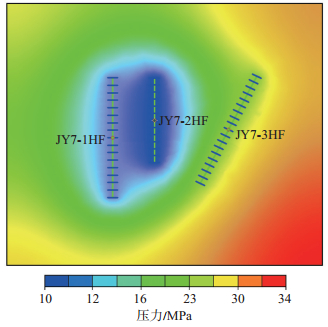
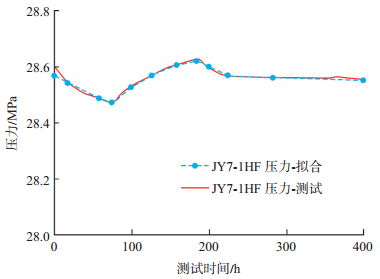
利用激动井关井阶段对应的观察井压力作半对数曲线拟合分析[20],该过程与常规压力恢复解释过程一致。根据井位图建立地质模型,并对模型划分网格。在所建立的数值试井模型的基础上进行压力历史拟合,结果如图 6和图 7所示。
|
下载eps/tif图 图 6 压力场模拟 Fig. 6 Pressure field simulation |
|
下载eps/tif图 图 7 压力史拟合曲线 Fig. 7 Pressure history fitting curve |
针对JY7-1 HF井和JY7-2 HF井的干扰测试,分别采用压力场数值模拟分析和压力史曲线拟合方法进行干扰解释。从干扰测试曲线的定性分析上,明确JY7-2 HF井和JY7-1 HF井之间存在干扰,采用压力历史拟合的方法,并利用数值试井技术计算得到了储层的渗透率为18.5 mD。虽然建立的地质模型是整个储层的,但观察井的压力只受激动井和观察井间的连通导压系数影响。因此,采用数值试井模型解释出的渗透率依然是井间的连通渗透率,不能将该渗透率理解为整个储层的渗透率。
4 结论(1) 近年来,随着页岩气井压裂规模的不断扩大、井距的不断缩小,井间干扰问题日趋严重。页岩气井之间的相互干扰一方面造成气井压力下降速度快、不利于生产,另一方面在压裂规模相对均衡的条件下说明井间储层连通性好,可有效控制井周围储层内的资源。实际上多数页岩气井各压裂段的改造规模并不均衡,干扰主要是由井间部分压裂效果较好的、空间距离较近的层段连通造成的。
(2) JY7-1 HF井和JY7-2 HF井的井间连通性较好,后期生产过程中应稳产控产,避免邻井频繁更换工作制度。建议后期井网部署时应根据单井设计产能,优化井距及各段压裂规模,对于与邻井水平段距离较近的层段应控制压裂规模。若已经出现较为严重的干扰,则须要及时控制本井与邻井的产气量,适时开展干扰定量化测试,以及表征干扰程度。
| [1] |
张小龙, 张同伟, 李艳芳, 等. 页岩气勘探和开发进展综述. 岩性油气藏, 2013, 25(2): 116-122. ZHANG X L, ZHANG T W, LI Y F, et al. Research advance in exploration and development of shale gas. Lithologic Reservoirs, 2013, 25(2): 116-122. DOI:10.3969/j.issn.1673-8926.2013.02.021 |
| [2] |
黄籍中. 四川盆地页岩气与煤层气勘探前景分析. 岩性油气藏, 2009, 21(2): 116-120. HUANG J Z. Exploration prospect of shale gas and coal-bed methane in Sichuan Basin. Lithologic Reservoirs, 2009, 21(2): 116-120. DOI:10.3969/j.issn.1673-8926.2009.02.025 |
| [3] |
蒋廷学, 王海涛, 卞晓冰, 等. 水平井体积压裂技术研究与应用. 岩性油气藏, 2018, 30(3): 1-11. JIANG T X, WANG H T, BIAN X B, et al. Volume fracturing technology for horizontal well and its application. Lithologic Reservoirs, 2018, 30(3): 1-11. |
| [4] |
AJANI A, KELKAR M. Interference study in shale plays. SPE 151045, 2012. |
| [5] |
KIM T H, LEE J H, LEE K S. Integrated reservoir flow and geomechanical model to generate type curves for pressure transient responses of a hydraulically-fractured well in shale gas reservoirs. Journal of Petroleum Science and Engineering, 2016, 146: 457-472. DOI:10.1016/j.petrol.2016.06.001 |
| [6] |
BELLO R O, WATTENBARGER R A. Multi-stage hydraulically fractured shale gas rate transient analysis. SPE 126754, 2010. |
| [7] |
OZKAN E, BROWN M L, RAGHAVAN R, et al. Comparison of fractured-horizontal-well performance in tight sand and shale reservoirs. SPE Reservoir Evaluation & Engineering, 2011, 14(2): 248-259. |
| [8] |
AL-RBEAWI S. Analysis of pressure behaviors and flow regimes of naturally and hydraulically fractured unconventional gas reservoirs using multi-linear flow regimes approach. Journal of Natural Gas Science and Engineering, 2017, 45: 637-658. DOI:10.1016/j.jngse.2017.06.026 |
| [9] |
STALGOROVA E, MATTER L. Practical analytical model simulate production of horizontal wells with Branch Fractures. SPE 162515, 2012. |
| [10] |
ZHANG L H, GAO J, HU S Y, et al. Five-region flow model for MFHWs in dual porous shale gas reservoirs. Journal of Natural Gas Science and Engineering, 2016, 33: 1316-1323. DOI:10.1016/j.jngse.2016.05.063 |
| [11] |
ZENG J, WANG X Z, GUO J C, et al. Composite linear flow model for multi-fractured horizontal wells in heterogeneous shale reservoir. Journal of Natural Gas Science and Engineering, 2017, 38: 527-548. DOI:10.1016/j.jngse.2017.01.005 |
| [12] |
WANG J L, JIA A L, WEI Y S, et al. Approximate semi-analytical modeling of transient behavior of horizontal well intercepted by multiple pressure-dependent conductivity fractures in pressuresensitive reservoir. Journal of Petroleum Science and Engineering, 2017, 153: 157-177. DOI:10.1016/j.petrol.2017.03.032 |
| [13] |
张旭, 蒋廷学, 贾长贵, 等. 页岩气储层水力压裂物理模拟试验研究. 石油钻探技术, 2013, 41(2): 69-74. ZHANG X, JIANG T X, JIA C G, et al. Physical simulation of hydraulic fracturing of shale gas reservoir. Petroleum Drilling Techniques, 2013, 41(2): 69-74. |
| [14] |
陈居凯, 朱炎铭, 崔兆帮, 等. 川南龙马溪组页岩孔隙结构综合表征及其分形特征. 岩性油气藏, 2018, 30(1): 55-62. CHEN J K, ZHU Y M, CUI Z B, et al. Pore structure and fractal characteristics of Longmaxi shale in southern Sichuan Basin. Lithologic Reservoirs, 2018, 30(1): 55-62. DOI:10.3969/j.issn.1673-8926.2018.01.006 |
| [15] |
张烈辉, 单保超, 赵玉龙, 等. 页岩气藏表观渗透率和综合渗流模型建立. 岩性油气藏, 2017, 29(6): 108-118. ZHANG L H, SHAN B C, ZHAO Y L, et al. Establishment of apparent permeability model and seepage flow model for shale reservoir. Lithologic Reservoirs, 2017, 29(6): 108-118. DOI:10.3969/j.issn.1673-8926.2017.06.014 |
| [16] |
余江浩, 王登, 王亿, 等. 湖北西部上二叠统大隆组页岩气资源潜力评价. 岩性油气藏, 2018, 30(4): 84-90. YU J H, WANG D, WANG Y, et al. Evaluation of shale gas resource potential of Late Permian Dalong Formation in western Hubei province. Lithologic Reservoirs, 2018, 30(4): 84-90. |
| [17] |
樊冬艳, 姚军, 孙海, 等. 考虑多重运移机制耦合页岩气藏压裂水平井数值模拟. 力学学报, 2015, 47(6): 906-915. FAN D Y, YAO J, SUN H, et al. Numerical simulation of multifractured horizontal well in shale gas reservoir considering multiple gas transport mechanisms. Acta Mechanica Sinica, 2015, 47(6): 906-915. |
| [18] |
CIVAN F, RAI S C, SONDERGELD H C. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transport mechanisms. Transport in Porous Media, 2010, 86(3): 925-944. |
| [19] |
YE Z H, CHEN D, PAN Z J. A unified method to evaluate shale gas flow behaviours in different flow regions. Journal of Natural Gas Science & Engineering, 2015, 26(C): 205-215. |
| [20] |
车世琦. 测井资料用于页岩岩相划分及识别——以涪陵气田五峰组-龙马溪组为例. 岩性油气藏, 2018, 30(1): 121-132. CHE S Q. Shale lithofacies identification and classification by using logging data:a case of Wufeng-Longmaxi Formation in Fuling Gas Field, Sichuan Basin. Lithologic Reservoirs, 2018, 30(1): 121-132. DOI:10.3969/j.issn.1673-8926.2018.01.012 |
 2018, Vol. 30
2018, Vol. 30




