2. 中国石油吐哈油田分公司勘探开发研究院, 新疆 哈密 839009
2. Research Institute of Exploration and Development, PetroChina Tuha Oilfield Company, Hami 839009, Xinjiang, China
随着油气勘探程度的不断加深,岩性油气藏已经成为当前油气勘探的重点领域,而保真叠前成像是岩性油气藏勘探的基础,因此,资料的保真叠前处理对于岩性油气藏的勘探就显得尤为重要[1]。保真成像取决于3个关键因素:一是要有适合观测孔径的规则化且无假频的叠前地震数据体,二是要有比较准确的宏观速度场,三是要有合适的成像方法[2-3]。保真的叠前成像对数据有具体的要求,不管是哪一种成像方法,都希望数据对成像体的照明是比较均匀和广角的,所记录的波前是完整的,并且在空间上的采样尽量是等间隔、无空间假频的[4-5],然而,在进行野外地震采集时,由于受地表采集条件或者观测系统设计参数不同等因素的限制,往往会造成地震数据出现道缺失或空间采样不足的问题,这样不仅会遗失有效的地质信息,而且会对后续资料处理产生不利的影响[6]。为了满足保真叠前成像的基础数据要求,必须要对叠前数据做规则化处理。
规则化处理讨论的内容主要涉及传统数学变换、低秩近似数据重建、压缩感知数据重建、高维数据重建及应用、海洋三维SRME去多次波数据规则化及应用等。目前,在规模化应用于商业软件并取得一定应用效果的插值方法中,ALFT方法在数据采样较密、无空间假频的情况下,对频谱估计的效果较好,但该方法无法克服空间假频[7-8];MWNI方法采用最小加权范数插值算法,选择自适应离散Fourier变换加权范数作为正则化项约束最小平方范数解,将重建数据的频谱形状作为先验信息加入迭代过程,用较少的数据就可以大致恢复信号的主要信息,但其约束条件操作性不强,难以兼顾精度和效率,只能取一个比较折中的方案[9-10];Low-Rank方法将数据重建视为求取多重Toeplitz矩阵的低秩近似矩阵问题,但该方法由于涉及矩阵向量乘法,计算效率较低[11-12];Radon谱约束下的线性信号重构方法结合正交多项式以及高分辨抛物Radon变换,将高阶高分辨Radon谱作为约束条件,对地震数据进行重建,能有效克服信号空间假频,对信号高、低频成分的恢复能力均较强,但是该方法对信号做了线性假设,对曲线的恢复误差较大[13-14];基于压缩感知理论的数据插值可以有效压制海洋自由表面多次波,但该方法要求原始数据无空间假频,且对信噪比要求较高,在低信噪比地区应用时会出现算法不稳定的情况[15-17]。综上所述,在目前应用较为广泛的方法中,ALFT、高精度Radon以及压缩感知类方法均要求原始数据不含空间假频,应用会受到限制,MWNI和Low-Rank类方法则计算效率均偏低,且对先验信息要求均较高,在复杂构造区无法实现规模化应用。
地震数据是五维的,但由于各种原因,极难保证地震观测系统在5个维度都很完美,如果仅在不同维度使用一维算法串联处理,则这种低维度算法串联处理不能有效利用已知信息,尤其不能适应陆地宽方位采集的不断发展,因此,亟须发展五维数据规则化方法。重点针对匹配追踪傅里叶插值(MPFI)方法进行研究,并在传统MPFI算法的基础上,采用不含假频信息的低频分量谱作为加权项,可以避免传统MPFI算法无法规避空间假频的弊端,同时可以在五维空间内完美地实现数据规则化处理。
1 传统MPFI方法对于保真处理而言,在偏移前进行插值和数据规则化处理都是十分必要的。目前,抗假频数据规则化、叠前三维地震数据体的五维重建等已经成为改善成像质量、提高资料保真性及保幅性的几项关键处理方法。在诸多方法中,傅里叶数据重建是常用的地震数据插值方法,该方法可以从二维扩展到更高维度空间。对于规则采样的数据,傅里叶数据重建非常有效,但对于非规则采样的数据,插值容易受到噪声污染,原因是在对非规则采样的数据进行离散傅里叶变换时,容易出现能量泄漏。
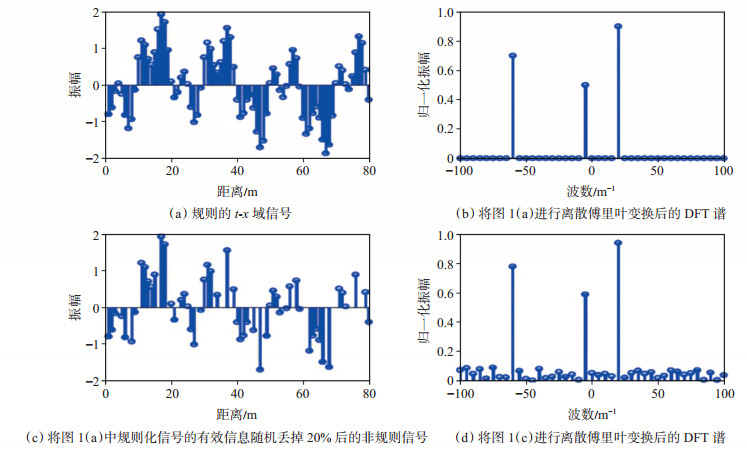
图 1(a)为规则采样的3个有效谐波信号,利用离散傅里叶变换将其转换至波数域[图 1(b)],相应在波数域也只有3个波数的谐波信号,其余波数的信号能量均为0,那么,规则采样的信号有且仅有3个谐波信号,与理论期望值是一致的。如果对图 1(a)所示相同的信号随机丢掉20%的有效信息,进行不规则采样[图 1(c)],再利用离散傅里叶变换将其转换至波数域,可以看到,虽然也有3个能量较强的谐波信号[图 1(d)],但其余波数信号的能量并不全为0,这就表明对于非规则的输入信号进行离散傅里叶变换,存在明显的能量泄漏。换言之,对于非规则采样的数据而言,不仅是快速傅里叶变换不能适应,而且本质上存在因非正交基而导致的能量泄漏,因此,规则化的过程实质上就是一个能量反泄漏的过程。
|
下载eps/tif图 图 1 输入数据及其通过离散傅里叶变换后的谱 Fig. 1 Input data and its spectrum after discrete Fourier transform |
防止谱泄漏的方法有很多,MPFI是近年来应用较多的方法。将匹配追踪应用于傅里叶变换并不是一个新的方法,Mallat等[18]提出了匹配追踪算法。近几年来,傅里叶变换逐渐被引入匹配追踪算法进行信号处理,同时,MPFI方法也被引入了地震资料处理来完成防泄漏的傅里叶变换,实现对非规则地震数据的规则化插值处理[19-20]。传统MPFI方法以傅里叶变换为基础,且该方法实现的前提条件是信号谱是稀疏的,但大部分野外采集的地震数据并不具备稀疏性,若将其变换到f-k域后,大部分谱值虽不等于0,但已很接近于0,只有很少的几个主要波数不为0,满足稀疏性的要求。也就是说,虽然t-x域的地震数据不具备稀疏性,但f-k域的地震数据可认为是稀疏的,稀疏采样数据可用一些主要的傅里叶系数即稀疏谱来表示[21]。
MPFI方法的基本思路是首先估算稀疏谱,然后对估算的稀疏谱开展傅里叶反变换,再将信号输出到期望位置。通常地震数据在时间方向的采样是规则的,具有一致的采样间隔,因此,通过快速傅里叶变换可将t-x域的数据稳定地变换至f-x域,但地震数据的空间采样通常是不规则的,需要对f-x域的输入样点作离散傅里叶变换,将其转换至f-k域后再迭代估算稀疏谱。传统的二维MPFI方法的实现步骤如下:①对非规则地震数据D开展空间离散傅里叶变换,并对每一个单频信号开展2~6步的迭代;②选取能量最大的傅里叶谱,并将其成分加入“估算谱”;③对所选能量最大的傅里叶谱成分开展傅里叶反变换,并按照输入位置输出迭代结果D1,此时D1即一个单频规则信号;④从非规则输入信号D中减去第③步迭代的单频规则信号D1,并对非规则地震信号D-D1开展空间离散傅里叶变换,再选取此时的最大傅里叶谱,将其分量加入第②步“估算谱”;⑤对此时所选的最大傅里叶谱成分开展傅里叶反变换,并按照输入位置输出迭代结果D2,此时D2为一个单频的规则信号;⑥事先设定迭代次数N或估算门槛值,并重复以上②~⑤步,直至满足规定迭代次数或残差小于门槛值为止(在极限情况下,即N趋于无穷大时,D=D1+D2+…+DN);⑦最终将迭代至第④步的“估算谱”通过傅里叶反变换重建数据,并将其输出到期望位置,便可得到规定迭代次数或门槛值的规则化地震信号。
在实际应用过程中,特别是在处理西部复杂陆地资料时,传统的MPFI方法并不能有效规避数据假频,尤其是被假频严重污染的高频信息。当假频能量与有效信号能量的级别基本相当时,用传统的MPFI方法很难准确地选取最大能量的傅里叶谱分量,此时就很可能会选中假频能量,从而出现错误的插值结果,最终导致地震数据整个规则化过程达不到保真的处理要求。由此可见,利用传统的MPFI方法进行地震数据规则化处理最难的环节是对含假频数据高频成分的有效恢复。
2 加权MPFI方法鉴于传统MPFI方法在应对复杂地表、复杂地下地质构造(“双复杂”构造)保真处理时存在的局限性,采用新的思路,将不易被假频污染的低频段信息作为先验信息对传统MPFI方法进行加权,并在计算估算谱前加入此权重,以实现反假频MPFI。加权MPFI方法的基本思路是:将地震数据中不易产生假频的低频分量作为先验信息估算先验值,并按一定权重将其应用于数据的高频成分,实现对数据的高频插值,达到恢复数据高频成分的目的,从而达到保真处理的要求。加权MPFI实现反假频的步骤为:①选取非规则采样的地震数据中不含假频的较低频率段信号,计算其频谱,并沿着不同倾角计算其能量谱;②对步骤①计算所得能量谱进行外推,并将此能量曲线作为权系数外推至高频和大波数端,在MPFI方法选取最大能量成分之前,对高频段傅里叶谱应用此权系数。此过程相当于对有效信号应用了较大权重,对假频信号应用了较小权重,重建f-k谱,以此得到的谱数据就很好地压制了非规则数据中的假频能量,达到了反假频插值的目的。
基于传统MPFI方法,结合上述反假频插值的基本思路,便可实现加权MPFI方法,其具体实现步骤为:①对空间采样不规则的地震数据开展空间离散傅里叶变换;②依据反假频基本思路计算并应用傅里叶谱权系数,以便能很好地区分加权后谱数据的有效信号和假频信号,由于假频信号所用权重较小,所以加权后假频能量会变得很弱,而有效信号谱分量的能量将得到放大;③选取加权后最大能量傅里叶谱分量,将未加权的该傅里叶谱分量加入“估算谱”(注意此时在“估算谱”中仅须加入原始未加权的傅里叶谱成分,而非加权后的傅里叶谱成分,第②步应用权重只是为了避免选中假频信号,是规避假频风险的一种手段,并不能代表其真实的能量值,否则会破坏插值后数据的相对能量关系,甚至出现假的插值结果);④利用离散傅里叶反变换将该未加权重的“估算谱”变换至t-x域,并按照输入位置输出相应的迭代结果;⑤此时按照传统MPFI方法的迭代思路,从原始输入的非规则数据中减去步骤④的迭代结果,并进行下一轮迭代,直至满足规定的迭代次数或残差阈值;⑥将步骤④最后一轮迭代出的“估算谱”通过傅里叶反变换重建数据,并将其输出到期望位置,便可得到规定迭代次数或残差阈值的不含假频且规则的地震信号。
从上述迭代过程可以看出,如果规定迭代次数过少或残差阈值过大,则所恢复原始数据中的有效信息就越少,这样虽然可节省一定的运算量,但会使原有地震数据信息大量损失;如果迭代次数足够多,就会恢复更多的原始数据信息,如果迭代次数无限大,基本会恢复所有的原始数据信息,但会大大增加计算量。因此,在应用过程中,应该根据处理要求,试验并确定迭代次数或残差阈值,以便确定最佳计算效果与计算效率的平衡点。
从上述加权MPFI方法的实现过程还可以发现,该方法只是改善了观测系统的空间采样属性,以便更好地满足后续处理的需求,并未额外加入地质信息,同时,该方法只是采用离散傅里叶变换及傅里叶反变换进行数学运算,且都是基于真实的炮、检点坐标实现的,因此,经过加权MPFI方法完成插值后的数据,在空间上有真实的炮、检点坐标,根据其各自站号信息,可以将含有真实坐标的插值数据抽到炮域,进而参与精度更高的炮域波动方程偏移。在一定计算能力的保障下,加权MPFI方法可完成二维到高维的扩展,实现高维度数据的加权MPFI,这样虽然会增加计算量,但是也可以提高变换估算的稳定性,而且随着目前并行计算效率的大幅度提高及GPU算法的商业化应用,采用高维度的加权MPFI方法,牺牲一定计算成本,换取稳定且保真的计算效果,是可以容忍的。
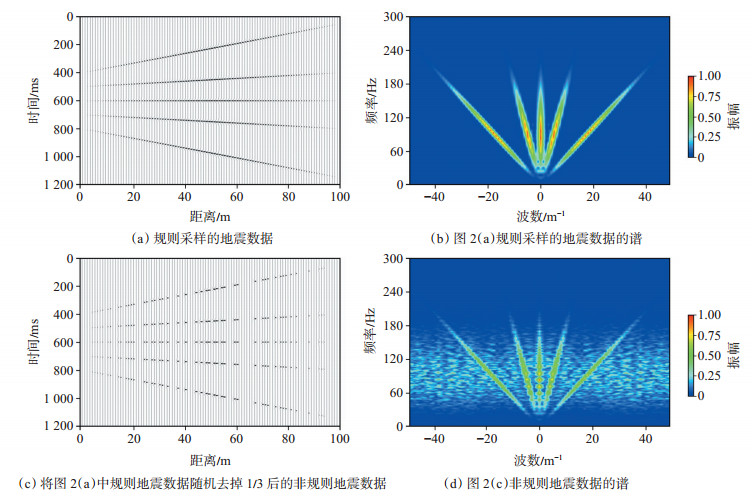
3 方法测试 3.1 正演模型测试为了验证加权MPFI方法的有效性,人工合成了一个包括5个线性同相轴的规则采样的地震数据及其谱[图 2(a)—(b)]。图 2(c)是将图 2(a)所示的规则地震数据随机去掉1/3后的非规则地震数据,图 2(d)是非规则地震数据图 2(c)的谱。对比图 2(b)和图 2(d)可以看出,非规则采样的地震数据其能量分布是失真的,无法满足保真处理的基本数据需求。
|
下载eps/tif图 图 2 含5个线性同相轴的正演数据 Fig. 2 Forward data with five sections |
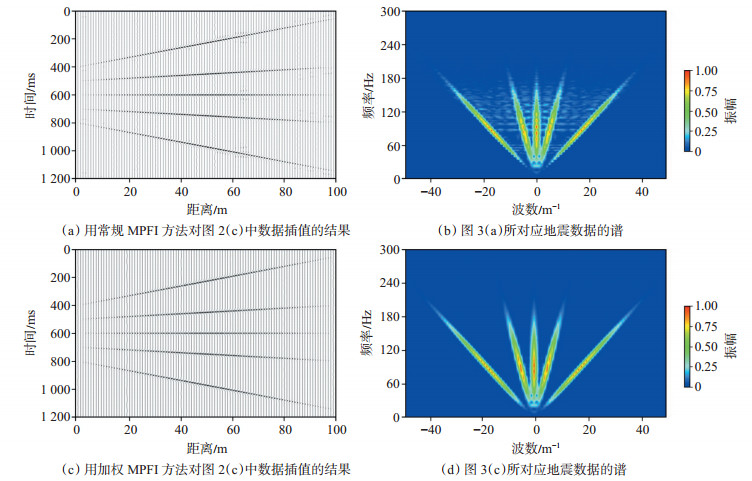
为了进一步证明加权MPFI方法相比于传统MPFI方法的优势,同时采用这2种方法对图 2(c)中非规则地震数据进行了插值处理,图 3为用2种方法插值后的效果对比。对比图 3(b)和图 3(d)可以看出,传统MPFI方法虽然在一定程度上恢复并弥补了一部分缺失数据,但仍然有部分数据是失真的,仍然无法满足保真处理的要求,而采用加权MPFI方法插值后,由于使用了不含假频的低频成分作为先验信息进行约束,因此,与传统MPFI方法插值效果相比,不仅弥补了所有缺失的地震道,而且其空间能量的分布也是非常均一且不含空间假频的,可以更好地满足保真、保幅叠前处理的需求。
|
下载eps/tif图 图 3 不同插值方法得到的地震数据及其谱 Fig. 3 Seismic data and spectra obtained by different interpolation methods |
为了验证加权MPFI方法对野外低信噪比地震数据规则化处理的能力和有效性,采用该方法对三塘湖盆地马朗凹陷马中地区实际资料进行了测试。工区位于马朗凹陷中东部,地面海拔为270~1 770 m,地表大部分为砾石覆盖的戈壁区及部分山体出露区,处于大型鼻隆构造带高部位,局部构造较多,二叠系、石炭系火山岩岩体发育,属于典型的“双复杂”构造区。该区块的勘探目标为二叠系火山岩岩性目标,并且要依据地震数据处理结果对岩性目标开展叠前反演,因此,对叠前资料的保真性提出了很高的要求[22-23]。该工区涉及5块三维地震资料连片处理,采集年限前后跨越20年,由于采集年限、采集参数、采集设备及地表条件等不同,导致5块地震资料在品质、覆盖次数(从30次至600次不等)、采集方位角(有3个不同的方位角)、采集面元(有25 m×25 m,25 m×50 m,50 m×50 m等3种类型)、炮线距、检波线距、纵横比、炮检线夹角及采集能量等方面均存在巨大差异,同时,由于存储介质异常,导致部分地震数据缺失,出现了炮、道丢失的现象,而覆盖次数不均匀、数据丢失及面元不统一等情况,往往会引起偏移划弧等问题,因此,必须对连片数据进行插值及规则化处理。
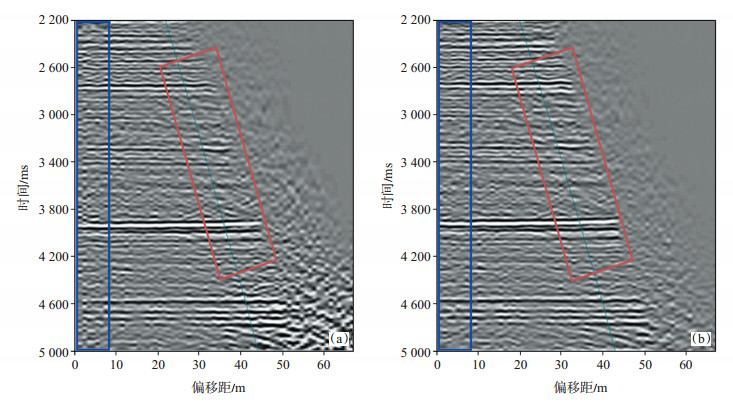
利用加权MPFI方法对数据进行了规则化插值处理。通过对比发现,经处理后炮、检点的分布与采集时的理论设计完全吻合,克服了因地表采集条件的限制而引起的炮、检点分布不均的问题,而且规则化后的炮、检点位置是按照理论设计的期望位置输出的,换言之,规则化后的炮、检点在空间上有真实的坐标,因此,规则化后的数据可以依据真实坐标反抽至炮域,也就是说,经加权MPFI方法处理后的地震数据可以实现基于波动理论的逆时偏移,这也是该规则化方法的优势之一。同时,与传统MPFI方法相比,采用加权MPFI方法插值后的数据偏移形成的CRP道集,近偏移距、远偏移距振幅特征改善明显,振幅随偏移距变化的趋势更加符合实际地质规律,更有利于叠前AVO属性的提取和叠前反演(图 4)。
|
下载eps/tif图 图 4 经传统MPFI方法(a)和加权MPFI方法(b)处理后形成的CRP道集 Fig. 4 CRP gathers processed by conventional MPFI method (a) and weighted MPFI method (b) |
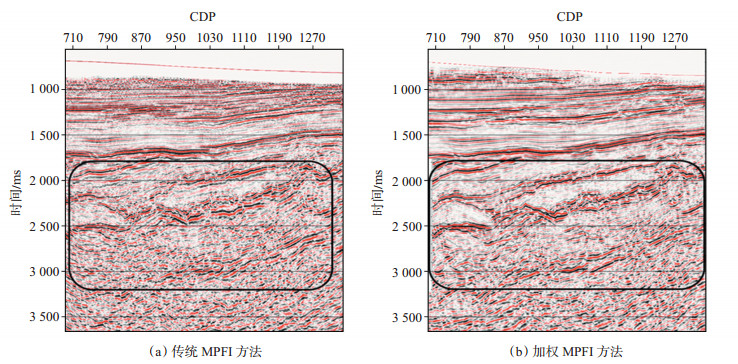
对比最终偏移结果(图 5)可以看出,采用加权MPFI方法开展连片处理可以提高OVT面元密度,改善Kirchhoff偏移效果,经该方法处理后的偏移结果从浅层至深层成像信噪比都得到了很大提高,火山岩岩性内幕反射更加清楚,小微断裂成像更加清晰,针对叠前CRP道集的反演结果与区内实钻井吻合程度较高,可见该方法能稳定而有效地处理较大数据空洞和不规则输入数据的规则问题。
|
下载eps/tif图 图 5 不同规则化方法叠前时间偏移结果 Fig. 5 Prestack time migration results obtained by different regularization methods |
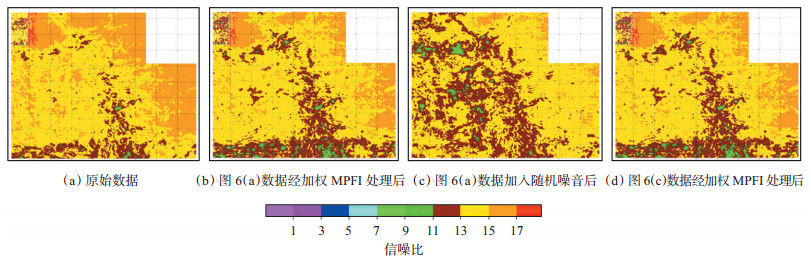
为了验证加权MPFI方法的抗噪性,对目的层段原始数据加入了不同比例的随机噪音。图 6(a)为未加入随机噪音的信噪比属性图(信噪比大于3的数据占81%),图 6(b)为对图 6(a)数据进行加权MPFI处理后的信噪比属性图,图 6(c)为对图 6(a)数据加入随机噪音后的信噪比属性图(信噪比大于3的数据占66%),图 6(d)为对图 6(c)数据进行加权MPFI处理后的信噪比属性图。对比图 6(b)和图 6(d)可知,对加入随机噪音的地震数据采用加权MPFI方法处理后,目的层段信噪比属性基本一致(信噪比大于3的数据均占89%),表明随机噪音不会影响该方法的应用效果,同时,规则化后的目的层段信噪比较规则化前高,进一步证明了该方法对于随机噪音具有一定的压制作用,可以同时达到规则化及压制随机噪音的目的。
|
下载eps/tif图 图 6 信噪比属性 Fig. 6 Attributes of signal-to-noise ratio |
(1)在传统MPFI算法的基础上,将不含假频的低频信息谱作为先验信息进行加权,实现了加权MPFI数据插值,并建立了规则化方法,即加权MPFI方法。通过数值模拟验证了该方法的准确性和有效性,通过对野外实测地震数据的测试,证实了该方法应用于三维连片处理,能更稳定而有效地处理较大数据空洞和不规则输入数据的规则化问题,可以解决多工区不同采集参数及数据缺失带来的空间采样不规则的问题,提高资料整体信噪比和成像质量,对于野外地震资料的适应性很好。
(2)与传统MPFI方法相比,加权MPFI方法采用了不含假频的低频信息作为先验值,具有更强的防能量泄漏和反假频的能力,能够提供更加规则的叠前数据。
(3)从地震数据处理角度讲,加权MPFI方法不会增加额外的地质信息,只是在一定程度上改善了观测系统的空间采样属性,而且经加权MPFI规则化后的地震数据,其炮、检点具有真实的空间坐标,可以反抽到炮域实现基于波动理论的成像方法。
| [1] |
王西文, 雍学善, 王宇超, 等. 面对重点勘探领域的地震技术研究和应用实效. 岩性油气藏, 2010, 22(3): 83-90. WANG X W, YONG X S, WANG Y C, et al. Study and application of seismic technologies for key exploration field. Lithologic Reservoirs, 2010, 22(3): 83-90. DOI:10.3969/j.issn.1673-8926.2010.03.016 |
| [2] |
杜金虎, 熊金良, 王喜双, 等. 世界物探技术现状及中国石油物探技术发展的思考. 岩性油气藏, 2011, 23(4): 1-8. DU J H, XIONG J L, WANG X S, et al. Status quo of international geophysical exploration technologies and thinking about the development of PetroChina geophysical exploration Technologies. Lithologic Reservoirs, 2011, 23(4): 1-8. DOI:10.3969/j.issn.1673-8926.2011.04.001 |
| [3] |
王靖, 孙赞东, 吴杰, 等. 地震资料处理方法的叠前保幅性研究. 岩性油气藏, 2016, 28(3): 105-112. WANG J, SUN Z D, WU J, et al. Pre-stack amplitude-preserved ability about several seismic data processing methods. Lithologic Reservoirs, 2016, 28(3): 105-112. DOI:10.3969/j.issn.1673-8926.2016.03.014 |
| [4] |
石颖, 张振, 王建民, 等. 地震数据反假频规则化方法研究. 地球物理学进展, 2013, 28(1): 250-256. SHI Y, ZHANG Z, WANG J M, et al. Investigation on anti-aliasing regularization approach for seismic data. Progress in Geophysics, 2013, 28(1): 250-256. |
| [5] |
GUO J, ZHENG Y, LIAO W Y. High fidelity seismic trace interpolation. SEG Technical Program Expanded Abstracts, 2015, 3915-3919. |
| [6] |
POOLE G, HERMAN P. Multi-dimensional data regularization for modern acquisition geometries. Expanded abstracts of 69th EAGE annual conference, 2007, 70-75. |
| [7] |
XU S, ZHANG Y, LAMBARE G. Anti-leakage Fourier transform for seismic data regularization in higher dimensions. Geophysics, 2010, 70(4): 87-95. |
| [8] |
SCHONEWILLE M, KLAEDTKE A, VIGNER A. seismic data regularization with the anti-alias anti-leakage Fourier transform. First Break, 2009, 27(9): 85-92. |
| [9] |
LIU B, SACCHI M D. Minimum weighted norm interpolation of seismic records. Geophysics, 2004, 69(6): 1560-1568. DOI:10.1190/1.1836829 |
| [10] |
NG M, WANG X S, NEGUT D. 6D interpolation by incorporating angular weight constraints into 5D MWNI. SEG Technical Program Expanded Abstracts, 2015, 3809-3813. |
| [11] |
ZHANG W, CHEN H L, ZHAO B, et al. 5D seismic data interpolation using low-rank radial function interpolation. SEG Technical Program Expanded Abstracts, 2016, 4118-4122. |
| [12] |
LI W C, ZHAO Y. An imaging perspective of low-rank seismic data interpolation and denoising. SEG Technical Program Expanded Abstracts, 2015, 4106-4110. |
| [13] |
SHAO J, WANG Y B, XUE Q F, et al. Radon-domain interferometric interpolation of sparse seismic data. SEG Technical Program Expanded Abstracts, 2017, 4343-4347. |
| [14] |
NIMSAILA K, WANG P. Fast progressives parse Tau-p transform for regularization of spatially aliased seismic data. Expanded Abstracts of 76th EAGE Annul conference, 2014, 230-234. |
| [15] |
杨敬磊, 余建鹏, 于建华, 等.基于压缩感知的数据规则化方法在三维数据重建中的应用.北京: SPG/SEG北京2016国际地球物理会议, 2016. YANG J L, YU J P, YU J H, et al. Application of data regularization techniques based on compressive sensing in 3D seismic data reconstruction. Beijing: SPG/SEG 2016 International Geophysical Conference, 2016. |
| [16] |
宋维琪, 张宇. 基于压缩感知理论的微地震资料噪声压制. 地球物理学展, 2017, 32(4): 1636-1642. SONG W Q, ZHANG Y. Noise suppression of the micro-seismic data based on the compressive sampling theory. Progress in Geophysics(in Chinese), 2017, 32(4): 1636-1642. |
| [17] |
WANG B F. Comparison of the POCS and IHT methods for seismic data interpolation and denoising. SEG Technical Program Expanded Abstracts, 2016, 4845-4849. |
| [18] |
MALLAT S G, ZHANG Z F. Matching pursuits with time-frequency dictionaries. IEEE Transactions on Signal Processing, 1993, 41(12): 3394-3415. |
| [19] |
段文胜, 王鹏, 党青宁. 应用匹配追踪傅里叶插值技术实现OVT域连片处理. 石油地球物理勘探, 2017, 52(4): 669-677. DUAN W S, WANG P, DANG Q N. 5D data regularization based on matching pursuit Fourier Interpolation for the OVT domain data merging processing. Oil Geophysical prospecting, 2017, 52(4): 669-677. |
| [20] |
NGUYEN T, WINNETT R. Seismic interpolation by optimally matched Fourier components. SEG Technical Program Expanded Abstracts, 2011, 30: 3085-3089. |
| [21] |
TANG J, YAN Z M, DUHOON N, et al. 5D matching pursuit Fourier interpolation and its application in surface-related multiple elimination for large offset coil data. SEG Technical Program Expanded Abstracts, 2017, 4758-4762. |
| [22] |
刘俊田, 张代生, 黄卫东, 等. 三塘湖盆地马朗凹陷火山岩岩性测井识别技术及应用. 岩性油气藏, 2009, 21(4): 87-91. LIU J T, ZHANG D S, HUANG W D, et al. Volcanic rock lithology recognition technique and its application in Malang Depression, Santanghu Basin. Lithologic Reservoirs, 2009, 21(4): 87-91. DOI:10.3969/j.issn.1673-8926.2009.04.017 |
| [23] |
杨占龙, 肖冬生, 周隶华, 等. 高分辨率层序格架下的陆相湖盆精细沉积体系研究:以吐哈盆地西缘侏罗系-古近系为例. 岩性油气藏, 2017, 29(5): 1-10. YANG Z L, XIAO D S, ZHOU L H, et al. Depositional system of lacustrine basins within high-resolution sequence framework:a case of Jurassic to Paleogene in western Turpan-Kumul Basin. Lithologic Reservoirs, 2017, 29(5): 1-10. DOI:10.3969/j.issn.1673-8926.2017.05.001 |
 2019, Vol. 31
2019, Vol. 31



