法国巴黎盆地枫丹白露砂岩为纯砂岩储层[1],由体积分数99.8%的石英和少量黏土矿物(体积分数<0.2%)组成,颗粒相对较细,平均颗粒直径大约250 μm(晶粒大小一般为150~300 μm),粒度分布相对均匀,圆度好,分选好,孔隙度和渗透率的变化范围均较大,孔隙微观图像呈圆形、椭圆形[2]。枫丹白露砂岩具有颗粒间相互接触的逾渗网络[3],在低含水饱和度下,导电薄膜的拓扑连接差异是其非阿米奇(Archie)现象的原因。
目前针对出现的非Archie现象,国内外学者对致密砂岩储层岩电参数的影响因素和变化规律开展了大量研究。车宇[4]在致密砂岩孔隙结构参数与电性关系的研究中,调研了温度、压力和润湿性等对岩电参数的影响;据文献[5]报道,Keller于1953年讨论了岩石湿润性对其电阻率的影响,得出n值的变化受岩石颗粒湿润性的影响,即使在相同的含水饱和度(Sw)下,润湿性的不同也会导致电阻率的差异;Diedrex [6]通过测量来自北海Rotliegend产气层5口井的亲水砂岩岩样,实验结果显示,有3口井的RI-Sw曲线均在含水饱和度降低的过程中出现了弯曲现象,据此推测在低含水饱和度时,由于黏土矿物中的残存水使得颗粒表面具有一定导电性;Swanson [7]利用空气-水银毛管压力法从实验角度证明了Diedrix [6]的结果;黄蓬刚[8]发现,当含水饱和度较低时,水膜对岩石导电性影响更加严重,当水膜厚度增加,电阻率明显减小,这主要是因为含水饱和度较低时,地层水主要为束缚水;李秋实等[9]认为地层因素F与储层孔隙度、孔隙曲折度、孔喉比有关,当孔隙度一定时,孔喉比越小,F值越低,饱和度指数n值的大小主要受储层孔喉比的影响;目前主要采用气驱法、离心法、烘干法、半渗透隔板法和自吸增水法等[10]测定b和n。
在储层识别、含油气饱和度评价和测井解释与评价方面,岩石的电阻率参数具有重要意义。影响电性数据非Archie现象的因素较多,有微观孔喉结构、润湿性以及黏土的附加导电性等[17],比如,泥质砂岩[12]微观孔隙结构对富含黏土体系导电性的影响[13]。低渗透油藏[14],储层各向异性[16],微观孔隙曲折度,流体分布[18]和润湿性[19]等情况下,Archie经典线性关系已不适用。在实验和理论分析基础上各种新的导电(饱和度)模型也越来越多,但目前对储层岩石电性参数的变化规律和影响因素的认识还不完善,故须对储层岩电实验关键参数进行准确地测定。通过枫丹白露砂岩电性实验研究,探寻电性参数(a,b,m,n)与孔隙度、渗透率等的变化规律,并用新的导电模型进行数据分析,辅以薄片和电镜资料,进而提高复杂测井含油气饱和度解释的精度,以期有效评价致密储层的开发潜能。
1 理论基础岩电参数测定的理论基础是Archie [21]公式,其分别利用岩样孔隙中完全饱和不同矿化度水的不同孔隙度纯砂岩岩样的电阻率R0和部分含水砂岩的电阻率Rt测量数据研究了地层因素(F)与孔隙度(Φ)、电阻率增大系数(RI)及含水饱和度之间的关系。1960年,测井分析家们对Archie公式进行扩展与延伸,形成了目前广泛使用的Archie扩展式
| $ \mathit{F}{\rm{ =}}\frac{{{\mathit{R}_{\rm{0}}}}}{{{\mathit{R}_{\rm{w}}}}}{\rm{ =}}\mathit{a}{\mathit{\Phi }^{{\rm{-}}\mathit{m}}} $ | (1) |
| $ \mathit{RI}{\rm{ =}}\frac{{{\mathit{R}_{\rm{t}}}}}{{{\mathit{R}_{\rm{0}}}}}{\rm{ =}}\mathit{bS}_{\rm{w}}^{{\rm{-}}\mathit{n}} $ | (2) |
式中:F为地层因素;RI为电阻率增大系数;R0为100%饱和盐水砂岩电阻率,Ω·m;Rt为饱和地层水和烃类物质岩石电阻率,Ω·m;Rw为地层水电阻率,Ω·m;Sw为含水饱和度;Φ为孔隙度;m为胶结指数;n为饱和度指数;a与b均为岩性系数。
Archie统计了大量实验数据,发现双对数坐标下,地层因素F与孔隙度Φ近似呈一条直线,但目前越来越多的学者观察到使用传统的Archie公式在致密储层含油气饱和度解释与评价中显示出了较为明显的不适应性,即产生了非Archie特性。
Tang等[22]经过对单孔隙介质的研究,得到单孔隙介质的电传导定量模型,并对这些模型中大量描述岩石微观结构的参数进行简化后,获得了单孔隙介质电阻率指数模型
| $ \mathit{RI}{\rm{ =}}\frac{{\mathit{C}{{{\rm{(}}\mathit{z}{\rm{-}}{\mathit{z}_{\rm{c}}}{\rm{)}}}^\gamma }}}{{{\mathit{C}_{\rm{w}}}{{{\rm{(}}\frac{{{\mathit{R}_{\rm{w}}}}}{\mathit{R}}{\rm{)}}}^{\rm{2}}}{{{\rm{(}}{\mathit{z}_{\rm{w}}}{\rm{-}}{\mathit{z}_{\rm{c}}}{\rm{)}}}^{{\gamma _{\rm{w}}}}}{\rm{ + }}{\mathit{C}_{\rm{h}}}{\rm{(}}\frac{\mathit{h}}{\mathit{R}}{\rm{)(}}\mathit{z}{\rm{-}}{\mathit{z}_{\rm{c}}}{{\rm{)}}^\upsilon }}} $ | (3) |
式中:Rw为含水孔隙空间的水力半径,μm;R为岩石水力半径,μm;h为水膜厚度,μm;z为平均配位数;zw为水相配位数;zc为临界配位数;C与γ均为与孔隙分布情况有关的参数;Ch与υ均为与孔喉分布变异系数有关的函数;Cw与γw均为与含水孔隙空间孔喉半径的变异系数有关的参数。令
| $ {\mathit{C}_{\rm{0}}}{\rm{ =}}\frac{{{\mathit{C}_{\rm{h}}}{{{\rm{(}}\mathit{z}{\rm{-}}{\mathit{z}_{\rm{c}}}{\rm{)}}}^\upsilon }}}{{\mathit{C}{{{\rm{(}}\mathit{z}{\rm{-}}{\mathit{z}_{\rm{c}}}{\rm{)}}}^\gamma }}}\frac{\mathit{h}}{\mathit{R}} $ | (4) |
| $ B'{\rm{ =}}\frac{{{\mathit{C}_{\rm{w}}}}}{\mathit{C}}\frac{{{\rm{(}}{\mathit{z}_{\rm{w}}}{\rm{-}}{\mathit{z}_{\rm{c}}}{{\rm{)}}^{{\gamma _{\rm{w}}}}}}}{{{{{\rm{(}}\mathit{z}{\rm{-}}{\mathit{z}_{\rm{c}}}{\rm{)}}}^\gamma }}} $ | (5) |
| $ {\left( {\frac{{{\mathit{R}_{\rm{w}}}}}{\mathit{R}}} \right)^{\rm{2}}}{\rm{ =}}\mathit{S}_{\rm{w}}^\mathit{n} $ | (6) |
式中:C0为与水膜厚度h有关的常数,当水膜厚度较小时,忽略水膜厚度对岩石电性的影响;B'描述了孔隙的连通性,与含水饱和度有关。
经过对单孔隙介质和孔隙-裂缝双重介质电传导性质的研究,提出新模型,并结合逾渗理论引进了B',该参数不是常数,它随着含水饱和度的变化而变化,对其进行化简处理可得到电阻率指数模型
| $ RI{\rm{ =}}\frac{1}{{ B'\mathit{S}_{\rm{w}}^\mathit{n}}} $ | (7) |
根据式(3)的变换式可计算出不同含水饱和度Sw下B'的取值,从而可拟合1/B'与Sw间的函数关系。通过对Archie公式进行非线性处理,即认为岩石胶结指数m与孔隙度Φ有关
| $ F{\rm{ =}}{\mathit{\Phi }^{{\rm{-}}\mathit{m}}} $ | (8) |
| $ m =f\left( \mathit{\Phi } \right) $ | (9) |
新模型继承了逾渗理论的普适性,适用于常规均质储层、强非均质性储层和致密储层,以及Archie非线性的情形也同样适用。结合式(1),(7)—(9)可得到能够进行工程应用的饱和度解释模型
| $ {\mathit{S}_{\rm{w}}} ={\left( {\frac{{{\mathit{R}_{\rm{w}}}}}{{B'{\mathit{\Phi }^m}{R_{\rm{t}}}}}} \right)^{\frac{1}{n}}} $ | (10) |
根据法国巴黎盆地枫丹白露纯砂岩储层的特征,选取了低孔渗、中孔渗、高孔渗等3个孔渗范围的岩样进行实验研究。
2.1.1 基本物性测试本文选取了9块不同孔渗的枫丹白露砂岩进行岩电实验,样品直径为2.5 cm左右,长度为5.3 cm左右。根据枫丹白露砂岩9个岩样物性数据的统计(表 1),孔隙度为0.03~0.15,平均值0.087;渗透率变化范围较大,为0.1~1000.0 mD,平均值220.6 mD。
|
|
下载CSV 表 1 枫丹白露砂岩样品参数 Table 1 Basic parameters of Fontainebleau sandstone |
渗透率是评价储层优劣的主要指标,按渗透率大小可将储层分为5级(表 2),根据储层分类评价标准,将9块枫丹白露砂岩分为低孔渗、中孔渗、高孔渗等3种不同等级的砂岩储层,其中,低孔渗砂岩3块(孔隙度0.033~0.052,渗透率0.111~0.262 mD),中孔渗砂岩2块(孔隙度0.079~0.086,渗透率37.625~46.994 mD),高孔渗砂岩4块(孔隙度0.095~0.149,渗透率110.577~901.388 mD),并分别对其进行讨论与分析。
|
|
下载CSV 表 2 储层渗透率分级 Table 2 Classification of reservoir permeability |
枫丹白露砂岩的电性影响因素复杂,运用储层岩样的铸体薄片和扫描电镜(图 1)可研究微观孔隙结构[23-25]及其对非Archie现象的影响。从鉴定结果可知,枫丹白露砂岩黏土矿物含量较低,石英发育成熟,粒间孔缝发育。一类样品如图 1(a)—(c)所示,枫丹白露砂岩样品全貌,可见其结构疏松,粒间孔缝发育,连通性良好,地层水为连续状,分布较均匀,使得岩石导电性较好,岩电实验数据分布符合经典的Archie线;另一类岩样如图 1(d) —(f)所示,为放大的粒间孔和石英加大之后的剩余粒间孔,分布较均匀,呈梯形或多边形状,但以点状或细管状孔喉为主,配位数0~2,孔隙整体连通性差,这也说明存在微小孔喉,使得孔隙结构变得复杂,当岩石含水饱和度降低时,地层水逐渐变成非连续状,且分布不均,降低了孔隙间的连通性,使得岩石导电性变差,电阻率迅速增大;另外如图 1(f)可知,岩样偶见波状消光,微裂纹,裂缝的存在对岩石导电性也存在重大影响,如图 1(b)可知,岩样颗粒间分离和晶粒表面可以看到水膜,水膜的存在会降低有效的喉道直径并阻碍岩石内部流体的流动,从而对岩石电阻率产生重大影响,这些都是岩石岩电实验中非Archie现象的影响因素。

|
下载eps/tif图 图 1 枫丹白露砂岩铸体薄片和扫描电镜图 (a)样品全貌,结构疏松,石英颗粒轮廓清晰,粒间孔缝发育,连通性良好,F13-7,SEM;(b)石英颗粒趋于自形,粒间孔缝发育,连通性良好,F15-2,SEM;(c)样品全貌,结构疏松,石英颗粒轮廓清晰,粒间孔缝发育,连通性良好,F22-4,SEM;(d)放大的粒间孔,点状孔喉,单偏光,F11-25,铸体薄片;(e)石英加大之后的剩余粒间孔,单偏光,F11-25,铸体薄片;(f)石英加大之后的剩余粒间孔,单偏光,F11-24,铸体薄片 Fig. 1 Casting thin sections and SEM images of Fontainebleau sandstone |
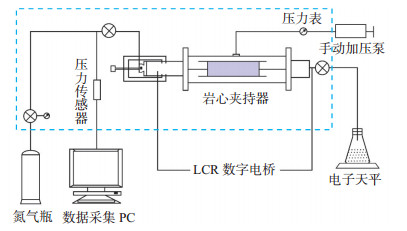
本次岩电实验中涉及到的主要实验装置有:电热恒温鼓风干燥箱、White-stone孔渗测试仪、电子天平、秒表、盐水配置系统、抽真空加压系统、岩心夹持器、MD-Ⅱ型毛管压力电性联测仪、TH2810 B型LCR数字电桥设备等。图 2为气驱法岩电实验装置示意图。
|
下载eps/tif图 图 2 气驱法岩电实验装置示意图 Fig. 2 Diagram of rock electrical experiment device for gas drive method |
参照中国石油天然气行业标准《SY/T 5385—2007岩石电阻率参数实验室测量及计算方法》设计方案,采用气驱降水法进行岩石电性实验,步骤如下:①岩样的选取。对已选岩样进行洗油、洗盐、烘干后测量岩样长度、直径、干重;②测量岩样物性。利用White-stone孔渗测试仪,测量岩心孔隙度,连接皂模流量计测定渗透率,并进行克氏校正;③配置并饱和模拟地层水。地层水矿化度为50 000 mg/L,抽真空加压(20 MPa)饱和地层水24 h后称饱和重,用数字电桥设备测量室温下(15.8 ℃)的盐水电阻率(0.209 Ω·m),并用图版法进行对比和校正;④岩电参数的确定。根据不同渗透率岩样施加不同的围压和驱替压力,记录不同温度下100%饱和条件和不同含水饱和度下的岩心电阻率;⑤实验结果分析及讨论。根据已测数据绘制F-Φ和RI-Sw关系图,可得到Archie公式的4个关键参数(a,b,m,n)。
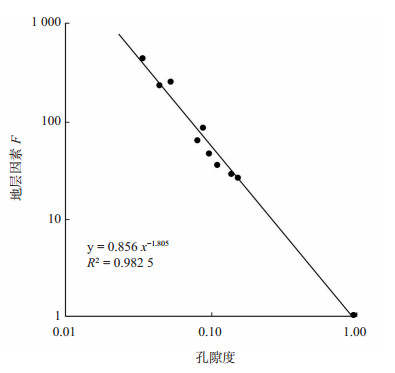
3 实验结果分析及讨论 3.1 地层因素与孔隙度的关系将法国巴黎盆地枫丹白露砂岩的测定数据采用Archie公式拟合F(图 3),在双对数坐标中,可看出F-Φ的拟合关系较好,呈现出明显的负相关关系,胶结指数m=1.805,岩性系数a=0.856,相关系数R2=0.982 5。这是因为孔隙度和渗透率的大小在一定程度上反映了岩样孔隙结构的复杂性,孔隙度和渗透率越大,孔隙空间连通性越好,孔隙结构越简单,孔隙间地层水相互连通且导电性较好,岩石电阻率越低,根据Archie公式,地层因数F就越小。
|
下载eps/tif图 图 3 地层因素F-孔隙度Φ关系 Fig. 3 Relationship between formation factor F and porosity Φ |
利用Archie公式分别对低孔渗、中孔渗和高孔渗枫丹白露砂岩的岩电实验数据(RI-Sw)进行拟合。
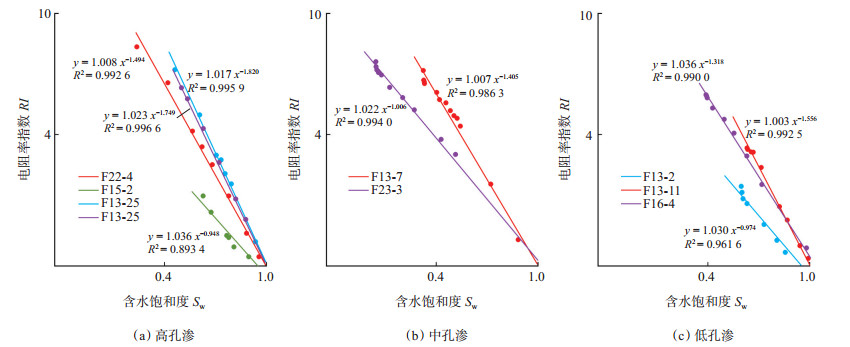
3.2.1 高孔渗样品图 4(a)显示,高孔渗岩样的实验数据点分布在经典Archie线(a=1,m=2)附近,为线性关系。饱和度指数n为0.948~1.820,岩性系数b为1.008~1.036。从拟合相关性可以看出,4块岩样的拟合效果都很好。这4块高孔渗岩样的拟合结果说明枫丹白露砂岩在高孔渗时孔隙间连通性较好,地层水为连续状,岩石导电性较好。
|
下载eps/tif图 图 4 枫丹白露砂岩的RI-Sw关系 Fig. 4 Relationships between RI and Sw of Fontainebleau sandstone |
图 4(b)显示,F13-7和F23-3等2块中孔渗岩样的饱和度指数n为1.006~1.405,岩性系数b为1.007~1.022。在含水饱和度较高时(0.3~1.0),这2块中孔渗岩样显示出经典的Archie现象,但随着含水饱和度的继续降低,这2块中孔渗岩样分别在含水饱和度0.18和0.29时出现一定程度的向上弯曲,表现出相对明显的非Archie现象。此时,岩样的孔隙结构出现了较明显的变化,表明随着含水饱和度的降低,孔喉连通性变差,孔隙结构变得复杂,地层水逐渐变成非连续状,岩石导电性变差,电阻率增加速度变快。
3.2.3 低孔渗样品图 4(c)显示,F13-11,F16-4和F13-2等3块低孔渗岩样的饱和度指数n为0.974~1.556,岩性系数b为1.003~1.036,且低含水饱和度下均出现更为明显的非Archie现象。
中、低孔渗枫丹白露砂岩的岩电实验数据拟合结果表明,刚开始驱替岩样的时候,含水饱和度较高,储层物性较好,孔隙结构简单,孔隙连通性好,地层水较连续,导电性较强,随着含水饱和度的降低,岩样中的地层水分布比较均匀,表现出经典的Archie现象,但随着含水饱和度的继续降低,大孔隙喉道被不导电物质取代,孔隙结构变得复杂,孔隙通道曲折度变大,导电流体主要存在于小孔隙喉道中,孔喉受到压缩连通性变差,地层水逐渐变成非连续状,岩石导电性变差,电阻率增加速度变快,曲线向上弯曲。另外在低含水饱和度时,随着孔隙结构复杂性的变化,黏附在孔隙和喉道壁上的水膜[26]对电阻率影响也增大,这些水膜显著降低了有效孔喉直径并阻碍流体的流动,不改变孔隙的几何形状,不会对孔隙体产生很大变化,但是对于喉道,效果很显著,当电流通过水膜时,电阻率值会迅速增大。
综上讨论分析,对于不同孔渗的枫丹白露砂岩样品,随着含水饱和度的逐渐降低,电阻率指数表现出明显的差异。孔渗大小影响其电阻率指数和含水饱和度曲线的变化趋势,低孔渗岩样随着含水饱和度降低到一定程度时,由于储层物性较差,微观孔隙结构复杂,孔隙连通性变差[27],出现了明显的非Archie现象。
根据9块岩样的RI-Sw岩电数据拟合关系结果可以得出岩电参数(b,n),具体的结果如表 3所列。
|
|
下载CSV 表 3 枫丹白露砂岩Archie基本参数及拟合关系 Table 3 Archie basic parameters and fitting relationships of Fontainebleau sandstone |
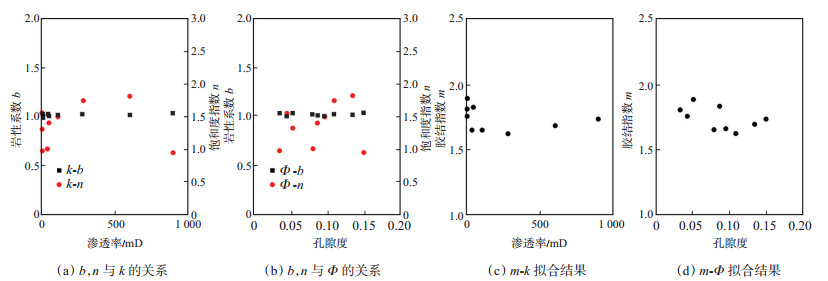
通过对单个岩样的m及拟合得到的b,n与孔隙度、渗透率数据进行拟合(图 5)。
|
下载eps/tif图 图 5 b,n,m与物性参数的关系 Fig. 5 Relationships between b, n, m and physical properties |
根据枫丹白露砂岩的b-k,n-k与b-Φ,n-Φ线性回归相关系数(表 3)可知,n为0.948~1.820,b为1.003~1.036,m为1.6~1.9。对于这批枫丹白露砂岩样品,图 5(a)—(b)显示,b与孔隙度和渗透率的关系均不大;n与渗透率的平方相关性较好,与孔隙度的平方相关性较差,且与孔隙度关系较复杂。图 5(c)—(d)显示,随着孔隙度和渗透率的增大,m与k,Φ具有一定的相关性,表明m在一定程度上受岩石孔隙度和渗透率的影响,但影响较小,关系较复杂。
岩石胶结指数m和岩石饱和度指数n都是对孔隙结构特征的表征,不同结构特征的岩石其m,n值均不同。一般来讲,储层孔隙结构越复杂,储集性能越差,储集层电阻率越高,则m值越小,n值越大[28];储层孔隙结构越简单,储集性能越好,m值越大,其n值越小。均质性好的储层,岩石m受孔隙度大小影响较小,随着孔隙结构变得越复杂,n和m除均受微观孔隙结构[29]的影响外,温度、压力、泥质含量、地层水矿化度和围压等也是其影响因素。总之,n和m与孔隙度和渗透率的关系较为复杂,但m的变化范围不大。
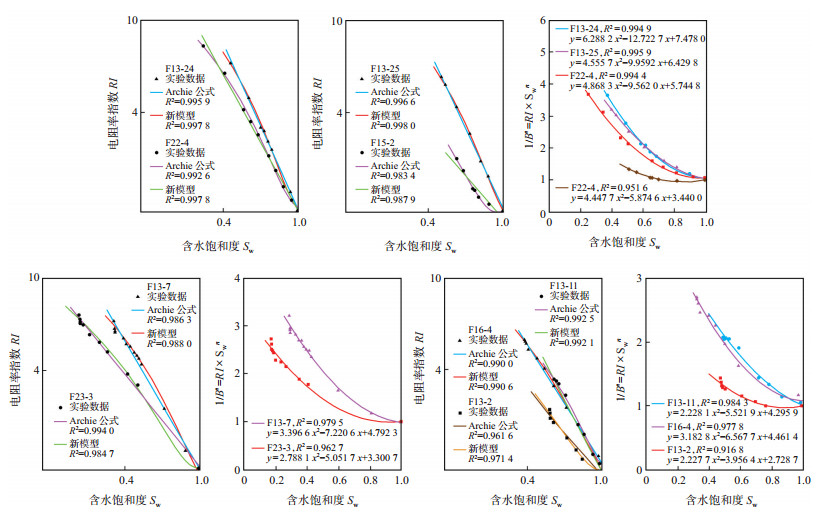
3.4 新模型的拟合结果通过新模型分别对低孔渗、中孔渗和高孔渗岩电实验数据进行拟合(图 6)。
|
下载eps/tif图 图 6 枫丹白露砂岩RI-Sw及1/B'=RI×Swn-Sw拟合结果 (a)(b)(c)高孔渗枫丹白露砂岩RI-Sw及1/B'=RI×Swn-Sw拟合结果;(d)(e)中孔渗枫丹白露砂岩RI-Sw及1/B'=RI×Swn-Sw拟合结果;(f)(g)低孔渗枫丹白露砂岩RI-Sw及1/B'=RI×Swn-Sw拟合结果 Fig. 6 Fitting results of RI-Sw and 1/B'=RI×Swn-Sw of Fontainebleau sandstone |
图 6中蓝色直线为使用Archie公式进行拟合所得结果;红色曲线为新模型的拟合结果,表明Archie公式和新模型拟合结果差别较大。从拟合关系可以看出基于逾渗理论的新模型更符合复杂条件下岩石电性的非线性特征;新模型的参数B'与含水饱和度Sw的拟合结果可看出,1/B'=RI×Swn-Sw拟合系数较高,拟合相关性较好。
新模型相比Archie公式拟合程度较高,其引进了与含水饱和度有关的孔隙连通性参数B',将孔隙结构的非均质性也考虑在内了,对于双对数坐标中电阻增大系数与含水饱和度非线性的情形也同样适用。
3.5 应用基于Archie公式和新模型,对于具体的含油气储层,通过相关井或储层的岩电实验数据拟合出Archie公式和新模型中所需的参数[30],获取地层水电阻率Rw,再根据孔隙度测井得到的地层孔隙度Φ和电阻率测井Rt得到的地层真电阻率,代入Archie公式和新模型中进行逐点计算,即可计算出储层的含水饱和度,进而可以获得含油气饱和度。
对Archie公式和新模型含油气饱和度解释结果进行对比与分析,最后优选出目的储层适宜的饱和度解释模型。
4 结论(1)法国巴黎盆地枫丹白露砂岩岩样可划分为3个范围,其中,高孔渗砂岩的实验数据点分布在经典Archie线(a=1,m=2)附近,为线性关系;中、低孔渗砂岩在低含水饱和度时均出现一定程度的向上弯曲,且低孔渗岩样表现出更明显的非Archie现象。微观孔隙结构是影响其非线性关系的主要因素,由于随着含水饱和度的逐渐降低,孔隙结构变得复杂,地层水逐渐变成非连续状,电阻率增加速度变快,向上弯曲,偏离Archie经典线性关系曲线。
(2)本次实验法国巴黎盆地枫丹白露砂岩岩样的饱和度指数n为0.948~1.820,胶结指数m为1.6~1.9,岩性系数b为1.003~1.036。b和m与孔隙度和渗透率的相关性均较差;n与渗透率的平方的相关性较好,与孔隙度的平方的相关性较差,且与孔隙度关系较复杂,这是因为n主要取决于孔隙的连通性,而渗透率能较好地表征孔隙间的连通性。
(3)通过对比Archie公式和新模型,对于本次法国巴黎盆地枫丹白露砂岩岩电实验数据拟合结果,基于逾渗理论的新模型能更好地反映岩石电性双对数坐标下的非线性特征。
致谢: 西南石油大学油气藏地质及开发工程国家重点实验室袁银春给予了热忱帮助,在此表示感谢!
| [1] |
REVIL A, KESSOURI P, TORRES-VERDÍN C. Electrical conductivity, induced polarization, and permeability of the Fontainebleau sandstone. Geophysics, 2014, 79(5): D301-D318. DOI:10.1190/geo2014-0036.1 |
| [2] |
BOURBIE T, ZINSZNER B. Hydraulic and acoustic properties as a function of porosity in Fontainebleau sandstone. Journal of Geophysical Research, 1985, 90(B13): 11524-11532. DOI:10.1029/JB090iB13p11524 |
| [3] |
YANICI S, ARNS J Y, CINAR Y, et al. Percolation effects of grain contacts in partially saturated sandstones:Deviations from Archie's law. Transport in Porous Media, 2013, 96(3): 457-467. DOI:10.1007/s11242-012-0099-5 |
| [4] |
车宇.致密砂岩孔隙结构参数与电学性质关系研究.成都: 西南石油大学, 2015. CHE Y. Study on the relationship between pore structure parameters and electrical properties of tight sandstone. Chengdu: Southwest Petroleum University, 2015. http://cdmd.cnki.com.cn/Article/CDMD-10615-1015605820.htm |
| [5] |
孙建国. 阿尔奇(Archie)公式:提出背景与早期争论. 地球物理学进展, 2007, 22(2): 472-486. SUN J G. Archie's formula:Historical background and earlier debates. Progress in Geophysics, 2007, 22(2): 472-486. DOI:10.3969/j.issn.1004-2903.2007.02.020 |
| [6] |
DIEDERIX K M. Anomalous relationships between resistivity index and water saturations in the Rotliegend sandstone (The Netherlands). SPWLA Twenty-third Annual Logging Symposium, 1982. |
| [7] |
SWANSON B F. Microporosity in reservoir rocks:its measurement and influence on electrical resistivity. SPWLA Twentysixth Annual Logging Symposium, 1985. |
| [8] |
黄蓬刚.低渗透砂岩储层岩石渗流电性特征研究: 以FJ及JZG储层为例.西安: 西安石油大学, 2012. HUANG P G. Study on seepage electrical characteristics of low permeability sandstone reservoirs: take the FJ and JZG reservoirs as an example. Xi'an: Xi'an Shiyou University, 2012. http://cdmd.cnki.com.cn/Article/CDMD-10705-1013156448.htm |
| [9] |
李秋实, 周荣安, 张金功, 等. 阿尔奇公式与储层孔隙结构的关系. 石油与天然气地质, 2002, 23(4): 364-367. LI Q S, ZHOU R A, ZHANG J G, et al. Relationship between Archie's formula and reservoir pore structure. Oil & Gas Geology, 2002, 23(4): 364-367. DOI:10.3321/j.issn:0253-9985.2002.04.013 |
| [10] |
游利军, 康毅力, 陈一健. 致密砂岩含水饱和度建立新方法-毛管自吸法. 西南石油学院学报, 2005, 27(1): 28-31. YOU L J, KANG Y L, CHEN Y J. New method of water saturation of tight gas-spontaneous imbibition. Journal of Southwest Petroleum Institute, 2005, 27(1): 28-31. DOI:10.3863/j.issn.1674-5086.2005.01.008 |
| [11] |
韩学辉, 李峰弼, 戴蕾, 等. 离心法和隔板法测量低渗透储层饱和度指数的对比. 中国石油大学学报:自然科学版, 2014, 38(6): 47-53. HAN X H, LI F B, DAI L, et al. Comparison of saturation exponent of low permeability reservoir obtained by centrifuge method and porous plate method. Journal of China University of Petroleum:Natural Science Edition, 2014, 38(6): 47-53. |
| [12] |
CLAVIER C, COATES G, DUMANOIR J. Theoretical and experimental bases for the dual-water model for interpretation of shaly sands. Society of Petroleum Engineers Journal, 1984, 24(2): 153-168. DOI:10.2118/6859-PA |
| [13] |
TABAGH A, COSENZA P. Effect of microstructure on the electrical conductivity of clay-rich systems. Physics and Chemistry of the Earth, 2007, 32: 154-160. DOI:10.1016/j.pce.2006.02.045 |
| [14] |
XIAO L, ZOU CC, MAO Z Q, et al. Estimation of water saturation from nuclear magnetic resonance (NMR) and conventional logs in low permeability sandstone reservoirs. Journal of Petroleum Science and Engineering, 2013, 108(15): 40-51. |
| [15] |
庞小军, 代黎明, 王清斌, 等. 渤中凹陷西北缘东三段低渗透储层特征及控制因素. 岩性油气藏, 2017, 29(5): 76-88. PANG X J, DAI L M, WANG Q B, et al. Characteristics and controlling factors of low permeability reservoirs of the third member of Dongying Formation in northwestern margin of the Bozhong Sag. Lithologic Reservoirs, 2017, 29(5): 76-88. DOI:10.3969/j.issn.1673-8926.2017.05.009 |
| [16] |
HARO C F. The equations Archie forgot:Anisotropy of the rocks. SPE 123913, 2010, 823-836. |
| [17] |
YUE W Z, TAO G. A new non-Archie model for pore structure:Numerical experiments using digital rock models. Geophysical Journal International, 2013, 195(1): 282-291. DOI:10.1093/gji/ggt231 |
| [18] |
MONTARON B. Connectivity theory:a new approach to modeling non-Archie rocks. Petrophysics, 2009, 50(2): 102-115. |
| [19] |
SUMAN R J, KNIGHT R J. Effects of pore structure and wettability on the electrical resistivity of partially saturated rocks:a network study. Geophysics, 1997, 62(4): 1151-1162. DOI:10.1190/1.1444216 |
| [20] |
韩学辉, 匡立春, 何亿成, 等. 岩石电学性质实验研究方向展望. 地球物理学进展, 2005, 20(2): 348-356. HAN X H, KUANG L C, HE Y C, et al. A view of the experimental study on rock electrical property. Progress in Geophysics, 2005, 20(2): 348-356. DOI:10.3969/j.issn.1004-2903.2005.02.016 |
| [21] |
ARCJIE G E. The electrical resistivity log as an aid in determining some reservoir characteristics. Petroleum Technology, 1942, 146: 54-61. |
| [22] |
TANG Y B, LI M, BERNABÉ Y, et al. A new electrical formation factor model for bimodal carbonates:Numerical studies using dual-pore percolation network. Geophysical Journal International, 2015, 201(3): 1456-1470. DOI:10.1093/gji/ggv073 |
| [23] |
闫建平, 梁强, 耿斌, 等. 低渗透砂岩微孔特征与孔隙结构类型的关系:以东营凹陷南斜坡沙四段为例. 岩性油气藏, 2017, 29(3): 18-26. YAN J P, LIANG Q, GENG B, et al. Relationship between micro-pore characteristics and pore structure of low permeability sandstone:a case of the fourth member of Shahejie Formation in southern slope of Dongying Sag. Lithologic Reservoirs, 2017, 29(3): 18-26. DOI:10.3969/j.issn.1673-8926.2017.03.003 |
| [24] |
曾源, 陈世加, 李士祥, 等. 鄂尔多斯盆地正宁地区长8油层组储层特征. 岩性油气藏, 2017, 29(6): 32-42. ZENG Y, CHEN S J, LI S X, et al. Characteristics of Chang 8 reservoir in Zhengning area, Ordos Basin. Lithologic Reservoirs, 2017, 29(6): 32-42. DOI:10.3969/j.issn.1673-8926.2017.06.005 |
| [25] |
况晏, 司马立强, 瞿建华, 等. 致密砂砾岩储层孔隙结构影响因素及定量评价:以玛湖凹陷玛131井区三叠系百口泉组为例. 岩性油气藏, 2017, 29(4): 91-100. KUANG Y, SIMA L Q, QU J H, et al. Influencing factors and quantitative evaluation for pore structure of tight glutenite reservoir:a case of the Triassic Baikouquan Formation in Ma 131 well field, Mahu Sag. Lithologic Reservoirs, 2017, 29(4): 91-100. DOI:10.3969/j.issn.1673-8926.2017.04.011 |
| [26] |
CHEN M, LI M, WANG Y, et al. The permeability of Fontainebleau sandstone to gases and liquids. Petroleum Science and Technology, 2016, 34(9): 845-852. DOI:10.1080/10916466.2016.1172087 |
| [27] |
李闽, 王浩, 陈猛. 致密砂岩储层可动流体分布及影响因素研究:以吉木萨尔凹陷芦草沟组为例. 岩性油气藏, 2018, 30(1): 140-149. LI M, WANG H, CHEN M. Distribution characteristics and influencing factors of movable fluid in tight sandstone reservoirs:a case study of Lucaogou Formation in Jimsar Sag, NW China. Lithologic Reservoirs, 2018, 30(1): 140-149. DOI:10.3969/j.issn.1673-8926.2018.01.014 |
| [28] |
罗少成, 成志刚, 周金昱, 等. 致密砂岩储层饱和度指数n计算方法研究. 西南石油大学学报(自然科学版), 2014, 36(4): 116-122. LUO S C, CHENG Z G, ZHOU J Y, et al. Research on saturation index n of tight sandstone reservoir. Journal of Southwest Petroleum University(Natural & Technology Edition), 2014, 36(4): 116-122. |
| [29] |
王维斌, 朱静, 马文忠, 等. 鄂尔多斯盆地周家湾地区长8致密砂岩储层特征及影响因素. 岩性油气藏, 2017, 29(1): 51-58. WANG W B, ZHU J, MA W Z, et al. Characteristics and influencing factors of Chang 8 tight sandstone reservoir of Triassic Yanchang Formation in Zhoujiawan area, Ordos Basin. Lithologic Reservoirs, 2017, 29(1): 51-58. DOI:10.3969/j.issn.1673-8926.2017.01.007 |
| [30] |
楚翠金, 夏志林, 杨志强. 延川南区块致密砂岩气测井识别与评价技术. 岩性油气藏, 2017, 29(2): 131-138. CHU C J, XIA Z L, YANG Z Q. Logging identification and evaluation of tight sandstone gas in the southern Yanchuan block. Lithologic Reservoirs, 2017, 29(2): 131-138. DOI:10.3969/j.issn.1673-8926.2017.02.016 |
 2019, Vol. 31
2019, Vol. 31



